基于并行计算的空间co-location模式挖掘*
和凤珍, 贾志洋, 张丹丹
(云南大学 旅游文化学院,云南 丽江 674100)
基于并行计算的空间co-location模式挖掘*
和凤珍, 贾志洋, 张丹丹
(云南大学 旅游文化学院,云南 丽江 674100)
提出适合并行计算的空间数据分区算法,并在此基础上提出基于并行计算的空间co-location挖掘算法.在三类数据集上做了大量的实验.实验结果表明,基于并行计算的算法在很大程度上提高了挖掘的效率,为进行空间大数据的挖掘提供了有效且快速的方法.
空间co-location模式挖掘;数据分区;并行计算;并行算法
空间co-location模式挖掘可以应用在很多领域中[1-3],它是从空间数据库中发现实例频繁关联的模式的过程,这些模式是一组空间特征的子集.目前,空间co-location 模式挖掘算法都是串行的数据挖掘方法[4-11].本文主要研究基于并行计算[12]的空间co-location模式挖掘.
1 空间数据分区
在并行数据挖掘中,为了提高挖掘效率,数据需要合理分割,否则会因处理机等待而影响算法执行的效率.中位数是一组数据中最中间的那一个,按照实例集横坐标或纵坐标的中位数对数据进行分割就可以保证负载的均衡.基于距离的空间co-location模式挖掘方法就是挖掘出满足邻近关系R的co-location模式[5],但在基于中位数的划分中有些满足邻近关系R的模式会分割到不同的区域,从而导致结果不具备完整性.为了避免这种情况,在分割空间数据时,区与区之间划出距离为距离阈值的一半(d/2)的交叉区域.这样保证了模式实例的不丢失,但中位数两边距离阈值的一半(d/2)的距离内的实例就会出现重复计算的情况,如果中位数的两边实例分布很稠密会浪费很多的时间.为了确保划分的高效性,提出基于中位数的横中轴划分与纵中轴划分两种.
定义1 (横中轴线/纵中轴线)过实例集y坐标的中位数且平行于x轴的线段称为横中轴线;相应的过x轴的中位数且平行于y轴的中轴线称为纵中轴线.
定义2 (左区/右区)把空间数据分成实例数相等的左右两个分块.左边由左边界到横中轴线向右平移d/2(d为邻近关系R的距离阈值)的区域组成,并称之为左区,简记Dl;右边由横中轴线向左平移d/2到右边界的区域组成,并称之为右区,简记Dr.
基于中轴线的划分法:①求出空间数据集x轴坐标的中位数;②求出空间数据集y轴坐标的中位数;③求出左右距纵中轴线均为d/2的区域内的实例数(m);④求出上下距横中轴线均为d/2区域内的实例数(n);⑤如果m大于n,则横中轴划分数据,否则纵中轴划分数据.
纵中轴划分:由纵中轴线把实例空间分为左区与右区的划分称为纵中轴划分,如图1所示.横中轴划分:由横中轴线把实例空间分为上区与下区的划分称为横中轴划分,如图2所示.
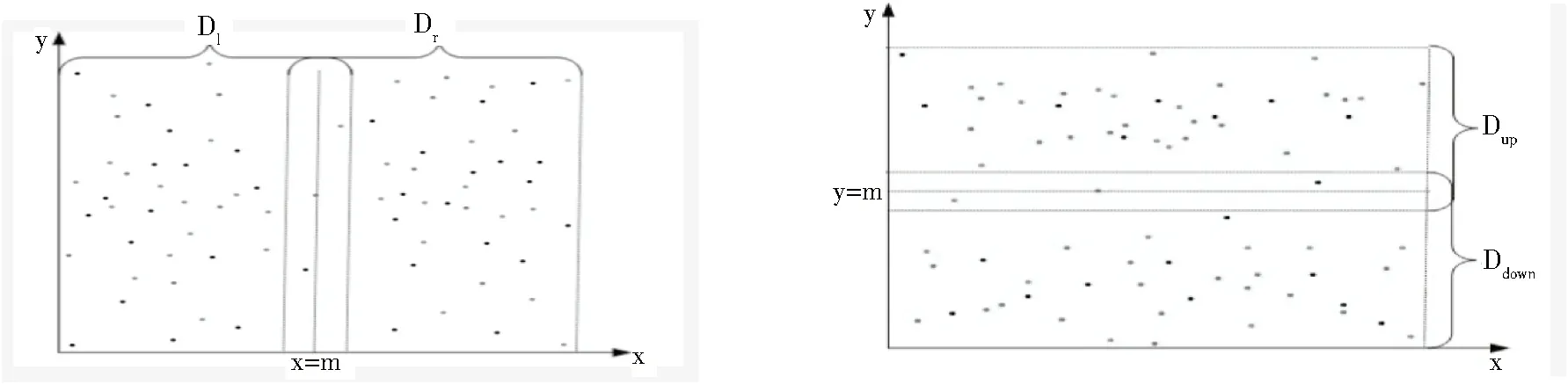
图1 纵中轴划分图 图2 横中轴划分图
基于以上分析,数据分区算法设计如下:
算法1:数据划分(div_domain)算法
输入:
空间特征集合:featureSet[n];空间实例集合:exampleSet[m].
输出:Dl(Dup),Dr(Ddown).
变量:
Ix:实例集x坐标的集合;Iy:实例集y坐标的集合;Xm:实例集x坐标的中位数;Ym:实例集y坐标的中位数;mx_d:x轴方向上的中位数左右d距离内的实例数;my_d:y轴方向上的中位数上下d距离内的实例数;Dl(Dup):左(上)区;Dr(Ddown):右(下)区;dis_threshold:距离阈值.
步骤:
1)Dl(Dup)=Φ;Dr(Ddown)=Φ;
Dx={exampleSet[1].x…exampleSet[m].x};Dy={exampleSet[1].y…exampleSet[m].y};//初始化变量
2)Xm=Gen_median(Dx);Ym=Gen_median(Dy);//求实例在x(y)轴方向上的中位数
mx_d=Count_example(Dx_d);my_d=Count_example(Dy_d);//求x(y)轴方向上距中位数左右各d/2距离内的实例数
3)数据分区
3.1)判断m与n的大小;
3.2)如果m大于n,则纵中轴划分空间,否则横中轴划分空间;
4)输出Dl(Dup),Dr(Ddown).
2 并行co-location模式挖掘算法
2.1 并行计算机处理机互连方式
采用TCP/IP通信协议来实现主机与辅机之间的通信.其中,主机采用服务器端编程方式,而辅机采用客户端编程的方式.
2.1.1 服务器端编程
为了使用TCP/IP来实现各主机间的通信,使用C#编程时,引用了TCP/IP通信接口类“usingSystem.Net.Sockets”.服务器端编程包括以下步骤:定义相关变量;定义监听函数;启动监听程序;接收并处理客户端信息.
2.1.2 客户端编程
在客户端的编程中使用C#编程,同样引用了TCP/IP通信接口“usingSystem.Net.Sockets”,客户端编程包括以下步骤:定义相关变量;建立与服务器的连接;监听并接收来自服务器的信息;向服务器发送信息.
2.2 全连接算法
全连接算法中候选模式及其实例的生成都是通过连接操作而得到的,即该算法在模式及实例的生成上类似于Apriori算法[1].此算法有两个最重要的步骤:候选模式生成和实例的生成.
生成候选模式:通过连接两个前k-2阶相同的k-1阶频繁模式来生成每一个k阶模式,每个生成k阶模式的k-1阶子模式都是频繁模式.
生成实例:设k阶模式c3是由k-1阶模式c1和c2连接得到,则模式c1和c2的表实例按照前k-2项相同进行连接.如果两个实例满足邻近关系R则连接得到模式c3对应的表实例.
算法2:全连接(Join-Base)算法
输入:
空间特征集合:featureSet[n];空间实例集合:exampleSet[m];邻近关系R的距离阈值:d;最小参与度阈值:min_prev;最小置信度阈值:min_cond_prob.
输出:频繁的空间co-location模式集合.
变量:
k:colocation的阶;Ck:k阶候选co-location集;Tk:Ck中的co-location表实例集;Pk:k阶co-location频繁集;T_Ck:Ck中k阶co-location的粗糙表实例集.
步骤:
1)co-locationsizek=1;C1=featureSet[n];P1=featureSet[n];
2)T1=generate_able_instance(C1,xampleSet[n]);
3)if(fmul=TURE)then
4)T_C1=generate_table_instance(C1,multi_event(E));//1阶粗糙表实例
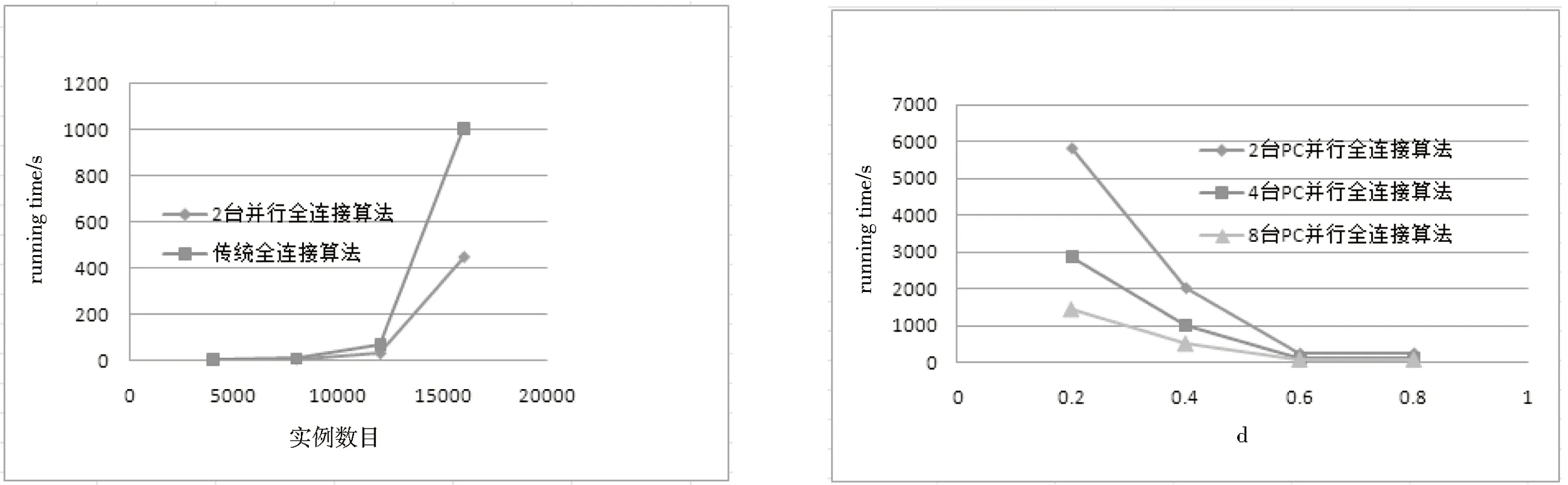
5)InitiallizedatastructureCk,Tk,Pk,Rk,T_Ck,tobeemptyfor1 6)While(notemptyPkandk 7)Ck+1=gen_candidate_colocation(Ck,k);//产生候选k+1阶co-location模式 8)if(fmul=TURE)then 9)Ck+1=multi_resolution_pruning(min_prev,T_Ck,multi_rel(R));//基于多分辨方法剪枝候选k+1阶co-location模式集 10)Tk+1=gen_table_instance(min_prve,Ck+1,Tk,R);//产生候选表实例 11)Pk+1=select_prevalence_co-location(min_prev,Ck+1,Tk+1);//计算候选参与度,产生频繁k+1阶co-location 12)Rk+1=gen_co-location_rule(min_prev,Ck+1,Tk+1);//基于条件概率阈值,产生频繁k+1阶co-location规则 13)k:=k+1;} 14)Return∪(R2,…,Rk+1); 2.3 基于并行计算的全连接算法 下面给出基于并行计算的新算法,该算法称之为PC-join-base算法,算法主要思想是使用局域网内的两台计算机来进行基于并行计算的全连接算法.一台计算机(PC1)求左区Dl(Dup)的表实例,另一台计算机(PC2)求右区Dr(Ddown)的表实例,求出每阶二个区域内的表实例后合并每阶的表实例得到相应阶的表实例,进而得到co-location频繁模式.具体挖掘过程如下: 算法3:PC-join-base算法 输入: 空间特征集合:featureSet[n];空间实例集合:exampleSet[m];最小参与度阈值:min_prev;最小置信度阈值:min_cond_prob 邻近关系R的距离阈值:d. 输出:频繁的空间co-location模式集合 变量: domain_width;domain_height;左(上)区:Dl(Dup);右(下)区:Dr(Ddown). 步骤: 1)在PC1中执行div_domain();//求出左区(上区)Dl(Dup)和右区(下区)Dr(Ddown); 2)由PC1把右区(下区)Dr(Ddown),发送到PC2; 3)并行执行3.1和3.2 3.1) 在PC2中求右区(下区)Dr(Ddown)的一阶表实例; waituntil(完成k+1阶表实例的求解过程); 将右区(下区)Dr(Ddown)的一阶表实例发送给PC1; 3.2) 在PC1中求左区(上区)Dl(Dup),的一阶表实例; 4)在PC1上合并Dl(Dup)和Dr(Ddown)的一阶表实例后得一阶频繁模式; 5)k=1;//k是阶数 do { 5.1) 在PC1上输出k阶频繁模式; 5.2) 向PC2发一个命令,让其继续应用join-base算法求右区(下区)Dr(Ddown)中的k+1阶表实例; 5.3) 并行执行5.3.1和5.3.2 5.3.1) 在PC2中waituntil(完成k+1阶表实例的求解过程) { 将PC2中右区(下区)Dr(Ddown)的k+1阶表实例发送给PC1;} 5.3.2) 在PC1上应用join-base算法求左区(上区)Dl(Dup)中的k+1阶表实例; 5.4) 在PC1上合并5.3.1和5.3.2中求出k+1阶表实例(去除其中冗余的行实例); 5.5) 在PC1上求出k+1阶表实例的参与度,从而生成k+1阶频繁模式; k++; }while(存在k阶的频繁模式) 2.4 剪枝策略 算法3在求解k+1阶表实例的过程中需要合并两台PC上的表实例,在这个过程可以用定理1对其进行剪枝. 定理1 如果k阶co-location模式P的左右两个区参与度之和小于最小参与度阈值,则任意P的超集模式P′是非频繁的. 证明 用算法1对数据进行分区时,左(上)区与右(下)区中间距中轴线左(上)右(下)d/2的区域是重叠的,如果k阶co-location模式P的左区与右区的参与之度之和小于最小参与度阈值,则必有PI(P) 3.1 算法的正确性与可扩展性 定理2 基于并行计算挖掘空间co-location模式挖掘算法是正确的. 证明 (1)证明基于纵中轴线划分的并行计算算法是正确的. 设Ei与Ej为所划分空间内的任意两个实例,Xm为实例集x坐标的中位数,Ei_x为实例i的x坐标值,Ej_x为实例j的x坐标值,d为距离阈值.则在划分中Ei与Ej分布有以下三种情况: a)Ei_x b)Xm-d/2≤Ei_x≤Xm且Xm≤Ej_x≤Xm+d/2; c)Ei_x (1.1) 如果Ei_x (1.2) 如果Xm-d/2≤Ei_x≤Xm且Xm≤Ej_x≤Xm+d/2,则Ei_x∈Dl,Ej_x∈Dl且Ei_x∈Dr,Ej_x∈Dr.此时Ei与Ej均在两台PC中,模式实例也不可能丢失. (1.3)如果Ej_x>Xm+d/2且Ei_x 综上,基于纵中轴线划分的算法是正确的. (2)同理可证基于横中轴线划分的并行算法是正确的. 基于并行计算挖掘空间co-location模式挖掘算法可继续按一分为二的形式扩展.由基于中位线的划分法可知,为了确保负载的均衡应该把实例空间分为实例数目相等的区域.那么可以把实例空间首先一分为二,再在两部分中分别使用基于中轴线的划分方法,依次在把每个部分一分为二.这样,经过n次就可以把实例空间分成2n个分块.可以分别把这2n个分块交给2n台处理机来计算. 3.2 算法的复杂度分析 3.2.1 算法2的时间复杂度分析 定理3 若含有m个特征的集合F中各特征的实例数基本相等,l为各个特征的平均实例数.这时全连接算法从i-1阶生成i阶模式的最坏时间复杂度为P′.其中i≥2. 证明 挖掘1阶模式的时间消耗为mL;生成i阶模式时,由于i-1阶表实例的最大长度为li-1,生成i阶表实例的前i-2阶(列)需比较O((li-1)2)次,对于前i-2阶的每一次连接,最后两列所需连接次数为li,这时i阶的时间消耗最大值约为: 3.2.2 算法3的时间复杂度分析 实验所用的两台PC的配置为Intel(R)Core(TM)i3-2100CPU3.10GHz,4G内存;操作系统为Windows7;开发平台为MicrosoftVisualStudio2008;开发语言为C#.实验所用的数据为三江并流区域老君山地带的真实植被数据.实验分析了距离阈值、参与度阈值和实例数目等对算法的影响,验证了基于并行计算的co-location模式挖掘算法的正确性以及高效性. 4.1 参与度阈值对算法的影响 考察参与度阈值的变化对算法执行时间的影响.特征个数为11,实例个数为65 535.距离阈值为30. 图3中可以看出:基于并行计算的co-location模式挖掘算法优于全连接算法.其他参数相同的情况下,空间co-location模式挖掘的运算量是随参与度阈值的增大而减小的.因此,当参与度阈值比较大的时候,基于并行计算的算法相对于全连接的优势不是特别明显.但参与度阈值比较小的时候连接操作很多算法运算量就很大,基于并行计算的算法明显优于全连接算法. 图3 参与度阈值对算法执行时间的影响 图4 距离阈值对算法执行时间的影响 4.2 距离阈值对算法的影响 考察距离阈值的变化对算法执行时间的影响.特征个数为10,实例总数为8 000,参与度阈值为0.7. 图4中可以看出:当距离阈值比较小的时候,由于计算量小,基于并行计算的co-location模式挖掘算法相对于基于全连接的算法优势不是很明显.但随着距离阈值增大运算量也增大,基于并行计算的算法明显优于全连接算法. 4.3 实例数目对算法的影响 考察实例数目的变化对算法执行时间的影响,距离阈值为30,参与度阈值为0.7.图5中可以看出:当实例数目较小时,基于并行计算的co-location模式挖掘算法的优势不太明显.但随着实例数目的增多,基于并行计算的算法的优势越来越明显. 图5 实例数目对算法执行时间的影响 图6 不同PC数目对算法执行时间的影响 4.4 PC数目对算法的影响 考察PC数目的变化对算法执行时间的影响.特征个数为11,实例个数为65 535,距离阈值为30. 图6中可以看出:随着PC台数的增加算法所用的时间也相应地减少.由于合并实例时花费了一小部分的时间,4台PC并行计算的时间略大于2台PC并行计算所花的时间的一半.同样的,8台PC并行计算的时间略大于4台PC并行计算所花的时间的一半. 将并行计算与空间co-location模式挖掘方法相结合,提出了一种基于并行计算的空间co-location模式挖掘算法.该算法基于中轴线来分割数据,因中轴线的性质确保了负载的均衡.在此基础上,统计x轴与y轴区与区之间重复部分的实例数而后选择实例数少的中轴线来分区使得在实例分布相对稀疏的区域分区,以此确保算法的高效性.实验分析表明,三类真实数据集上基于并行计算的空间co-location模式挖掘算法都优于基于全连接的空间co-location模式挖掘算法.基于并行计算挖掘空间co-location模式挖掘算法可继续按一分为二的形式扩展,为以后研究大规模的空间co-location数据提供了有效且快速的方法. [1]HUANGYAN,SHEKHARS,XIONGHUI.Discoveringco-locationpatternsfromspatialdatasets:ageneralapproach[J].IEEETransactionsonKnowledgeandDataEngineering,2004,16(12):1472-1485. [2] 王丽珍,陈红梅.空间模式控制理论与方法[M].北京:科学出版社,2004. [3]XIONGHUI,SHEKHARS,HUANGYAN,etal.Aframeworkfordiscoveringco-locationpatternsindatasetswithextendedspatialobjects[C].Proceedingsofthe12thAnnualACMInternationalConferenceonDataMining(SDM′04),LakeBuenaVista,USA,2004:1-12. [4]HUANGY,SHEKHARS,XIONGH.Discoveringco-locationpatternsfromspatialdatasets:ageneralapproach[J].IEEETransactionsonKnowledgeandDataEngineering,2004,16(12):1472-1485. [5]YOOJS,SHEKHARS.Apartialjoinapproachforminingco-locationpatterns[C].Proc.ofthe12thannualACMinternationalworkshoponGeographicinformationsystems,WashingtonDC,USA,2004:241-249. [6]HUANGY,ZHANG,LYUP.Canweapplyprojectionbasedfrequentpatternminingparadigmtospatialco-locationmining?[C].Proc.ofthe9thPacific-AsiaConferenceonKnowledgeDiscoveryandDataMining(PAKDD),Hanoi,Vietnam,2005:719-725. [7]YOOJS,SHEKHARS,CELIKM.Ajoin-lessapproachforco-locationpatternmining:asummaryofresults[C].Proc.ofthe5thIEEEInt.Conf.onDataMining(ICDM2005),Houston,USA,2006:813-816. [8]WANGL,BAOY,LUJ,etal.Anewjoin-lessapproachforco-locationpatternmining[C].InThe8thIEEEInternationalConferenceonComputerandInformationTechnology,Sydney,Australia,2008:197-202. [9]WANGLIZHEN,BAOYUZHEN,LUZHONGYU.Efficientdiscoveryofspatialco-locationpatternsusingtheiCPI-tree[J].TheOpenInformationSystemsJournal,2011,3(1):69-80. [10]WANGLIZHEN,ZHOULIHUA,LUJOAN.Anorder-clique-basedapproachforminingmaximalco-locations[J].InformationSciences,2009,179(19):3370-3382. [11]WUPINGPING,WANGLIZHEN,ZHOUYONGHENG.Discoveringco-Locationfromspatialdatasetswithfuzzyattributes[J].JournalofFrontiersofComputerScienceandTechnology,2013,7(4):348-358. [12]SHEKHARS,CHAWLAS.Spatialdatabases:atour[M].UpperSaddleRiver,USA:PrenticeHall,2003. Mining Spatial Co-location Patterns Based on Parallel Computing HE Feng-zhen, JIA Zhi-yang, ZHANG Dan-dan (Tourism and Culture College,Yunnan University,Lijiang 74100,China) This article studies spatial co-location pattern mining on the basis of parallel computing. We proposed a novel co-location pattern mining algorithm based on parallel computing. We did lots of experiments on three data sets. Experiments showed that the novel algorithm based on parallel computing can greatly improve the efficiency of spatial data mining and provide a new method to mine mass spatial data in a fast and effective way. Spatial co-location pattern mining; Data partition; Parallel computing; Parallel algorithms 2014-11-24 国家自然科学基金资助项目(F020508);云南省教育厅科学研究基金重点资助项目(2012Z143C). 和凤珍(1988-),女,云南丽江人,硕士研究生,助教,主要从事空间数据挖掘与分析方面研究. 和凤珍. TP311.13 A 1007-9793(2015)04-0056-073 算法分析与讨论
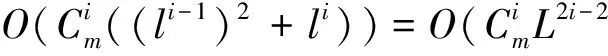
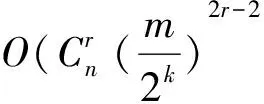
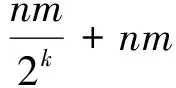
4 实验分析

5 总 结

