基于最小二乘法的项目化实训质量评价模型研究

汪松松

摘要摘要：对教学质量评价模型进行了定性和定量分析。为提高模型精度，在理清学生技能掌握程度与项目化实训教学各影响因素关系的基础上，引进校企合作企业评价因子，利用最小二乘法对项目化实训质量评价体系进行数学建模，以指导实训教学，提高教学质量。通过数据分析得知学生个人素质非常重要，需要在教学中注重综合素质的培养。

关键词关键词：项目化教学；质量评价；最小二乘法

DOIDOI：10.11907/rjdk.1431026

中图分类号：TP301

文献标识码：A文章编号

文章编号：16727800（2015）004004903

0引言

最小二乘法（又称最小平方法）是一种应用广泛的数学优化技术，本文采用最小二乘法对计算机类项目化实训课程进行了数学建模，得出质量评价模型，以此指导项目化实训教学。

高职培养目标主要定位在高技能人才的培养。在新的教学模式下，随着项目化教学的深入，各专业的职业技能课主要在机房、实训室等专业场所进行。与教室教学相比，无论从学生知识接受方式上和实践技能提高上都发生了本质变化。另外，校外实训不同于校内实训，校外实习注重学生在工作场合的适应性，校内实训主要是在专业教师的辅导下，提高专业知识和技能，实行“理实一体化”教学模式，是学生主要知识来源和主要能力训练场所。所以，有必要建立科学的项目化实训教学模型，定量研究实训质量影响因素与实训效果之间的关系。

1教学评价

国内外教育质量评价研究主要集中在评价因素方面，如生源质量、教学计划及实施过程质量、教学过程质量、课堂教学质量、教学辅助过程质量、教学条件质量、教师队伍质量及考试考核质量等。针对国内高职教育特点，我国学者深入研究了职业教育影响因素与教育质量的定性与定量关系，并提出各种先进的教学评价模型，但鲜见对项目化实训教学领域进行研究。

1.1质量评价模型定性研究

时会美、陆善兴、许芳奎等人[15]主要研究了教学质量评价体系建设的重要性、评价体系整体设计、评价因素结构等内容。

实训教学是高职实践教学的重要组成部分，学生实训质量评价体系包括校内实习实训评价和企业顶岗实习评价，对于校内实训质量评价，提出了能力标准的评价模式。高职校内实习实训质量评价指标由职业道德素质、专业能力（专业基本能力和专业综合能力）和创新能力3个方面组成，评价模式包括绝对评价、过程评价、综合评价，评价指标采用直接赋值法，评价分为5个等级：A，B，C，D，E，其中A=1，B=0.8，C=0.6，D=0.4，E=0.2。评价人根据评价表中各项内容对被评价学生作出相应评价，每一级每项指标相乘的成绩总和即为该学生的最终评价分数。

陆善兴设计了实习实训质量指标体系，该体系由实习实训参与者、实习实训内容、实习实训过程、实习实训环境和实习实训效果等8个要素构成，实行定量评价和定性评价、过程性评价与终结性评价、绝对性评价与相对性评价、校外评价与校内评价、自评与他评相结合，并建立了实习实训质量评价指标体系考评表，细化指标，增强可操作性。

许芳奎则主要研究了教师实践能力的重要性，认为教师的实践能力是教师知识、素质、技能等多方面因素的综合反映。基于教师实践能力的教学质量评价，目的在于检查与分析教师在实践教学中是否有针对性地培养了企业所期许的工作能力，以此判断教师是否具备实践教学能力。教师实践能力的教学质量评价主要包括教学设计评价、教学实施评价、教学效果评价，评价原则是目标、激励性、有效性等。

1.2质量评价模型定量研究

在教学质量评价模型研究方面，包含丽、於实、叶勇等人[68]深入研究了教学质量定量评价模型，主要方法有线性回归、偏最小二乘法、多元统计分析、灰色关联和层次分析法、模糊层次分析法、云模型课堂教学质量数据挖掘法等。

包含丽提出的最小二乘法评价模型克服了人为的主观随意性，能够正确反映评价要素与评价目标（教学效果）之间的关系。

为了提高评价精度，学者於实从教学效果、教学内容、教学方法和教学态度4个方面构建评价指标体系，充分考虑多位专家意见，应用层次分析法计算出各参评指标权重，并利用模糊数学挖掘出教学质量等级与参评指标之间的规则知识，建立了教学质量评价一致性判断矩阵。

叶勇认为，教学质量评价是一个多层次、多目标优化问题，系统非线性较强。为提高课堂教学质量评价效果，作者提出了一种基于云模型的课堂教学质量数据挖掘方法。采用支持向量机对课堂教学质量与评价指标间的非线性关系进行逼近，采用遗传算法进行支持向量机参数优化，采用云模型对遗传算法进行改进，提高全局搜索能力，以防止获得局部最优支持向量机参数。

1.3最小二乘法

最小二乘法是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知数据，并使得这些数据与实际数据之间误差的平方和最小。包含丽、杨建军、田垅等人[6，910]对最小二乘法的应用及改进算法进行了研究。最小二乘法在关系函数、数据拟合等领域应用非常广泛，与各种非线性、智能算法相比，具有算法简单、无人为影响等特点。改进的最小二乘法具有运算速度快、系统稳定等特点。把最小二乘法引入项目化实训质量评价具有科学可行性。

2实训质量评价指标体系

建立数学模型的首要任务是各参与因子的量化，评价模型量化精确度决定了模型的可用性。根据美国的教育评价理论，评价标准主要包括适当性（Propriety）、有效性（Utility）、可行性（Feasibility）和精确性（Accuracy）等。高等职业教育与社会生产实际联系紧密，强调培养的毕业生需具有较高的职业素养和职业技能。项目化实训课程主要围绕学生实践因素及效果打分。

基于工学结合校企合作的实训质量评价体系，质量影响因素主要体现在学生、学校、企业三方面。多年的教学与实践经验表明，在程序类课程中，较好的逻辑思维、良好的职业素质是软件开发的必备素质；学校课程组织、师资力量决定实训质量；企业提供的项目适合度及对教学支持度对实训教学亦很重要。

学生基础能力可在课程开始时进行测试，包括逻辑思维能力、意志力、专业基础等，是学生进一步学习的基础要素。学校主要提供理实一体化学习环境，包括具有吸引力的教学材料、知识丰富的师资队伍、科学的课程设置、政策支持、学习网站支持、教师的全过程跟踪管理与指导。在企业顶岗实践过程中，实践项目的覆盖面、合理度、吸引力、过程安排、时间安排、企业人员参与度等因素无不直接决定学生的实践能力。通过对学生实践能力目标评价指标的归纳与分析，得出评价指标体系如图1所示。

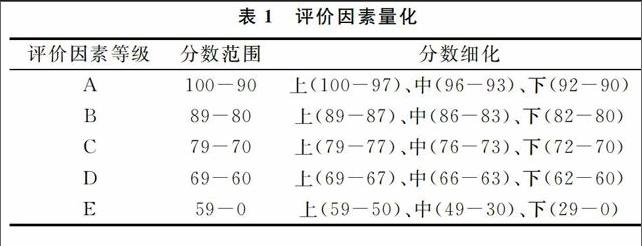
项目化教学评价因素及效果数值的确定是一个不可忽视的问题，为了精确定量课堂练习影响因数的数值，特别是部分很难界定的评价因素，如学生个人素质、基础能力等，可以先以五级制进行定性，再根据投票进行分数细化，如表1所示。3基于最小二乘法的实训质量评价模型

最小二乘法通过最小方差来拟合数据，尤其是用在线性二维数据上。由于项目化实训评价因素比较多，故需要使用线性多维拟合办法。设函数y=S*（x）为综合评分与评价要素关系，基于最小二乘法，找到多维线性函数y，使误差平方和为最小：

4计算机类课程实例分析

采样数据中，通过定性和定量来处理数据，在各分数段选取典型的成绩值，并对影响因子进行评估，获得影响因子数据。考虑到Matlab中Curve Fitting Toolbox（曲线拟合工具箱）只能提供二维数据的拟合和仿真，故采用regress（Y，X）或自行编程进行计算，得到其中意志力达到19.8%。

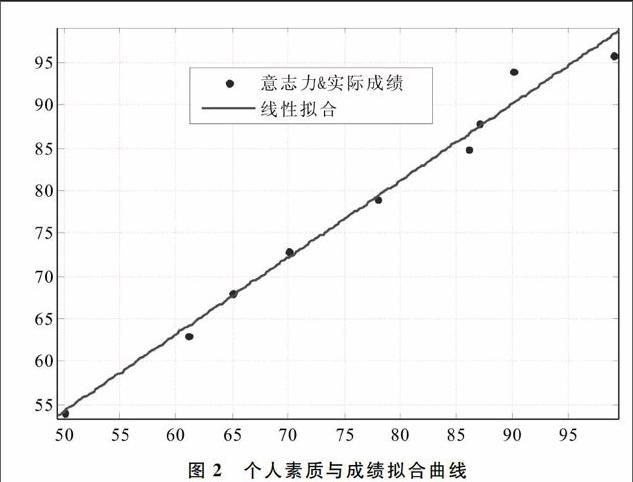
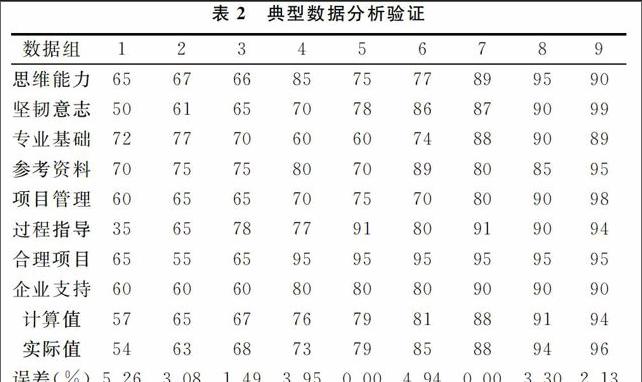
对得到的一组评价因子进行数据验证，分别选取不同分数层次数据进行对比分析，结果如表2所示。结果发现学生个人素质中意志能力是比较重要的一项参数，故单独列出进行线性回归，图形几乎是成正比例的，如图2所示。从这点来看，增强学生的综合素质，特别是在教学中鼓励学生不怕困难、敢于解决问题，并在其中寻找成功的乐趣是非常重要的。

5结语

最小二乘法项目化实训质量评价模型在实践教学指导中具有一定意义，可通过影响因素权值的大小来及时调整侧重点，提高项目化实训质量。最小二乘法的各影响因素之间假设为非相干状态，而事实上各影响因素间具有一定的相干性。考虑到评价综合效果，项目化实训过程可进一步转化为神经网络模型，通过反馈模式及时调整各影响因子的权值。同时，量化标准存在人为差异，但至少要确保量化数据相对准确，以提高模型精度。另外，值得注意的是，以企业需求为主导的高职培养机制应与学生的个人需求相结合，充分调动学生的学习积极性。

参考文献参考文献：

[1]时会美，张殿明. 高职学生实习实训质量评价体系的构建[J].职教论坛，2010 （9）：6769.

[2]陆善兴.高职院校实习实训质量评价指标体系构建[J]. 职业技术教育，2010， 31（2）：5962.

[3]许芳奎.基于实践能力的高职院校教师教学质量评价的探讨[J].教育与职业，2012 （12）：170172.

[4]刘伟.对高职设计艺术专业教学质量评价体系建设的探究[J].职教论坛，2010 （26）：5153.

[5]金佳雷.谈高职院校教学质量监控与保障体系的多元化构建[J].教育与职业， 2012 （24）：3637.

[6]包含丽. 基于最小二乘法的教学质量评价模型研究[J].温州大学学报， 2012，33（4） ：4448.

[7]於实.模糊层次分析法在教学质量评价中的应用研究[J].计算机仿真， 2012，29（6）：369372.

[8]叶勇.基于云模型的课堂教学质量数据挖掘[J].计算机仿真， 2012，29（8）：373376.

[9]杨建军，郑健龙.移动最小二乘法的近似稳定性[J].应用数学学报，2012，35（4）：637648.

[10]田垅，刘宗田.最小二乘法分段直线拟合[J].计算机科学，2012，36（6）：482484.

责任编辑（责任编辑：杜能钢）