三层媒质中的镜像法及其在普通电阻率测井中的应用

仵 杰，曹 婷

(西安石油大学 光电油气测井与检测教育部重点实验室，陕西 西安 710065)

三层媒质中的镜像法及其在普通电阻率测井中的应用

仵 杰，曹 婷

(西安石油大学 光电油气测井与检测教育部重点实验室，陕西 西安 710065)

将二层媒质中的镜像原理推广到三层媒质，建立点电流源位于任意位置时三层媒质中的电位计算解析公式，应用于计算三电极梯度电极系在三层地层中的测井响应。归纳总结测井响应特征与三电极在地层中的位置关系。电位与三层媒质镜像源的关系揭示了测井响应机理。利用COMSOL有限元软件数值计算验证了三层媒质镜像原理计算三电极梯度电极系测井响应的有效性。三层媒质镜像原理可用于获取各种电极系测井在三层导电媒质中的响应计算解析式，为电极系参数设计和响应特征分析提供理论依据。

镜像法；三层导电媒质；梯度电极系；视电阻率

恒定电流场中的点电流源在层状导电媒质中所产生的电位或电场是电法勘探和测井理论研究中的重要内容[1-5]。对于无限大均匀电各向同性导电媒质，点电流源产生的场的解析解与点电荷类似[6]。对于无限大二层导电媒质，可用镜像原理导出点电流源的解析解。对于三层或三层以上的导电媒质，通常使用模式匹配法和积分方程法获得近似解析解[5]。这些方法通常都含有复杂的积分，直接求解会遇到很大困难，有时只能进行近似计算。对于三层媒质，部分学者推广利用二层媒质中的镜像原理建立三层媒质的镜像原理。文献[7]利用镜像法求解了空气-海水-海床三层模型中位于海水中的任意方向静态点电偶极子在同层中产生的电位与电场分布。文献[8]在文献[7]的基础上，提出采用二次等效的方法，求解三层媒质中源位于中间层而场位于其他层媒质时的电场分布。但对源位于其他层时的场分布问题，只给出了推导思路，并未给出完整的表达式。在石油普通电阻率测井中，三层媒质是仪器设计和测井响应特征研究的基础。本文将利用镜像原理研究三层导电地层模型中点电流源在任意层中产生的电位和电场，并用于计算分析梯度电极系在三层地层中的响应特征。

1 三层导电媒质中镜像法的应用

图1为梯度电极系在三层地层中的示意图。电极系由电源电极A和测量电极M、N组成，电极A、M之间的距离大于电极M、N之间距离，电极A到电极M和电极N的中点的距离定义为梯度电极系的电极距，记为L。梯度电极系沿z轴放置，3个电极可以在三层地层中的任意一层。三层模型是构成复杂层状地层的基本模型。计算电极系在不同位置的测井响应是仪器电极系设计和测井响应特征分析的基础。

图1 梯度电极系与3层地层示意图

假设电源电极A的电流强度为I，在无限大均匀电各向同性地层中，可推出梯度电极系的视电阻率计算公式[9]

(1)

(2)

式(2)表明，对于给定电极系，K值是固定不变的。

下面研究三层导电媒质中的镜像法，多层导电媒质可做类似处理。

图1所示的三层地层可视为2个分界面z=0和z=D的叠加。发射电极A(x0,y0,z0)处的点电流源I在导电媒质中形成恒定电流场，在z=0和z=D两个分界面上满足边界条件：电流法向连续，电场切向连续。

当同时考虑2个分界面时，根据镜像原理通过多次镜像建立不同区域的电位[7]。点电流源I通过界面z=0(z=D)产生第一次镜像，第一次产生的镜像源又通过z=D(z=0)产生第二次镜像，第二次产生的镜像源又通过z=0和(z=D)产生第三次镜像，依次类推。下面详细研究怎样用镜像法求解三层导电媒质中点电流源在任意场点(x,y,z)处的电位表达式，根据源在地层中的位置分3种情形。

(1)点源位于中间层。文献[7]已推出，当上层媒质为绝缘媒质σ1=0，点源位于中间层时，同层的场点处产生的场可以用无穷多个镜像源在无限大的中间媒质产生的场的叠加来代替。文献[8]同样设点源位于中间层，先经过一次等效求出场源同层时的场分布，再利用二次等效的方法将三层媒质等效为2层，进而用镜像法求出异层场点的分布。有效地解决了上层为绝缘媒质σ1=0，点源位于中间层，场点位于任意层的场分布问题，但对于上层为导电媒质即σ1≠0的情况，并未给出明确的解。而在实际地层中遇到的多为导电媒质，因此，对σ1≠0时场分布问题的研究十分重要。下文采用文献[7-8]的方法对上层媒质为导电媒质，点源位于中间层，场点位于任意层的场分布问题进行处理。

当上层媒质为导电媒质，点源位于中间层时，点电流源及其所有通过界面镜像的源可根据其位置分为以下4组：

场点位于第1、2、3层媒质的电位分别为

(3)

(4)

(5)

其中：

式(3)—式(5)中：电位Φij的下标i=1、2、3表示点源位于第1、2、3层媒质中，j=1、2、3表示场点位于第1、2、3层媒质中。

(2)点源位于上层。当点源位于上层时，可根据点源距z=0界面的距离分为3种情况：

①点源距z=0的距离小于中间层厚度。点电流源I通过界面z=0产生的第一次镜像位于中间层，第一次产生的镜像源又通过z=D产生第二次镜像，第二次产生的镜像源又通过z=0产生第三次镜像，依次形成一组位置和表达式有规律的镜像源。点源先通过z=D界面镜像，镜像源再通过z=0界面镜像，这样依次往返镜像，也可形成一组位置和表达式有规律的镜像源。

②点源距z=0的距离大于中间层厚度且不成倍数关系。点电流源I通过界面z=0产生第一次镜像位于第三层，第一次产生的镜像源又通过z=D产生第二次镜像，第二次产生的镜像源又通过z=0产生第三次镜像，经过几次镜像后的镜像源又位于中间层，然后再类似于第一种情况在z=0和z=D两个界面上往返镜像，而前几次镜像源的表达式与镜像落入中间层后再通过界面镜像的表达式不一致，需要另作处理；点源先通过z=D镜像，再通过z=0镜像，依次在2个界面的往返镜像所得镜像源的表达式与第一种情况一致。

③点源位于z=0界面上或距z=0的距离与中间层厚度成倍数关系。点源在分界面上，或当点源距z=0的距离与中间层厚度成倍数关系时，会出现镜像源落到分界面的情况，不满足采用镜像法的前提条件，此时可以作如下处理：将位于边界上的点源移至上层紧靠边界的地方，这样对解答不会有影响[10]，又可以将问题归到(1)中；同理，距z=0的距离与中间层厚度成倍数关系的点源可以移至其上方紧靠的一个位置，可将问题归到(2)中。

下面将以点源距z=0界面的距离小于中间层厚度为例进行推导。对于点源距z=0界面的距离大于中间层厚度的情况可做类似处理。

在图1所示的三层模型中，位于上层中的点电流源在各层场点处所产生的场可以等效为图2所示的无穷多个镜像点电流源在场点分别产生的场的叠加。当场点位于上层时，点电流源在场点处产生的场可等效为，点电流源和其通过z=0界面的第一次镜像及通过2个界面的往返镜像中每次由z=D界面得到的镜像作为下次通过z=0界面的源在场点处产生的场的叠加，如图2(a)所示。此时，点电流源及其镜像源根据其位置和表达式可划分为以下4组：

①位于(x0,y0,z0)处，点电流源为I,场点距该组点电流源的距离为R01；

②位于(x0,y0,-z0)处，点电流源为-η1I,场点距该组点电流源的距离为R11；

图2 点源位于上层，场点处于不同媒质时镜像法的应用

则场点处的电位为如图2(a)，所有点电流源在上层场点处产生的电位的和为

(6)

其中：

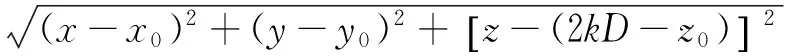
同理，当场点位于中间层和下层时，场点处的电位分别为图2(b)、图2(c)中，所有点电流源产生的电位的和分别为

(7)

其中：

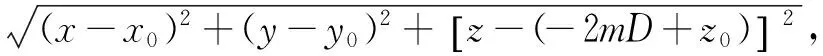
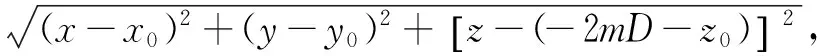
R1k、R2k表达式同前面所示。

(8)

其中：

R1m、R2m表达式同前面所示。

(3)点源位于下层。当点源位于下层，相当于源位于上层时将上层与下层的电导率互换，即可用同样的推导方法得到场点位于任意层的电位表达式。

2 用三层媒质镜像原理计算梯度电极系的测井响应

下面以单极供电底部2.5 m梯度电极系A2.25 M0.5N为例研究三层镜像原理的应用。如图1所示，底部梯度电极系位于任意位置时，通过测量电极的电位可以求出仪器的视电阻率(测井响应)。

根据电源电极A在地层中所处的位置，可分为以下几种情况：

(1)电源电极A位于上围岩，且距z=0界面距离小于高阻层厚度，此时

(9)

(10)

其中：

根据M和N的位置又分为3种情形。

①M、N位于上围岩，ΦM=Φ11(zM,zA),ΦN=Φ11(zN,zA)，

ΔUMN=ΦM-ΦN=Φ11(zM,zA)-Φ11(zN,zA)；

(11)

②M位于上围岩，N位于高阻层，ΦM=Φ12(zM,zA),ΦN=Φ12(zN,zA)，

算法种群的粒子全局最优的个体位置是通过对比粒子寻优过程中的每个粒子的个体极值来确定的,这个全局最优个体位置称为“全局极值”,即所有粒子节点部署节点最优位置。粒子群算法不断通过迭代优化地搜索并更新个体极值和全局极值,最终求得全局的最优位置。

ΔUMN=ΦM-ΦN=Φ11(zM,zA)-Φ12(zN,zA)；

(12)

③M、N位于高阻层，ΦM=Φ12(zM,zA),ΦN=Φ12(zN,zA)，

ΔUMN=ΦM-ΦN=Φ12(zM,zA)-Φ12(zN,zA)。

(13)

(2)电源电极A位于高阻层

(14)

(15)

其中：

根据电极M和N在不同位置分别计算不同电位差。

①M、N位于高阻层，ΦM=Φ22(zM,zA),ΦN=Φ22(zN,zA)，ΔUMN=ΦM-ΦN=Φ22(zM,zA)-Φ22(zN,zA)；

(16)

②M位于高阻层，N位于下围岩，ΦM=Φ22(zM,zA),ΦN=Φ23(zN,zA)，ΔUMN=ΦM-ΦN=Φ22(zM,zA)-Φ23(zN,zA)；

(17)

③M、N位于下围岩，ΦM=Φ23(zM,zA),ΦN=Φ23(zN,zA)，ΔUMN=ΦM-ΦN=Φ23(zM,zA)-Φ23(zN,zA)。

(18)

(3)电源电极A位于下围岩层，且距z=0界面距离小于高阻层厚度，

(19)

其中：

则有：M、N位于下围岩，ΦM=Φ33(zM,zA),ΦN=Φ33(zN,zA)，

ΔUMN=ΦM-ΦN=Φ33(zM,zA)-Φ33(zN,zA)。

(20)

将以上不同情况下求得的各ΔUMN代入式(1)可以计算梯度电极系的视电阻率。取R1=R3=1 Ω·m，R2=5 Ω·m，I=1 A，根据以上推导的公式，计算底部梯度电极系沿z轴正方向上层移动时的视电阻率，如图3(a)所示。为了解释视电阻率曲线，根据上述电位公式绘出了电极系沿z轴正方向移动时测量电极M、N的电位变化曲线，如图3(b)所示。

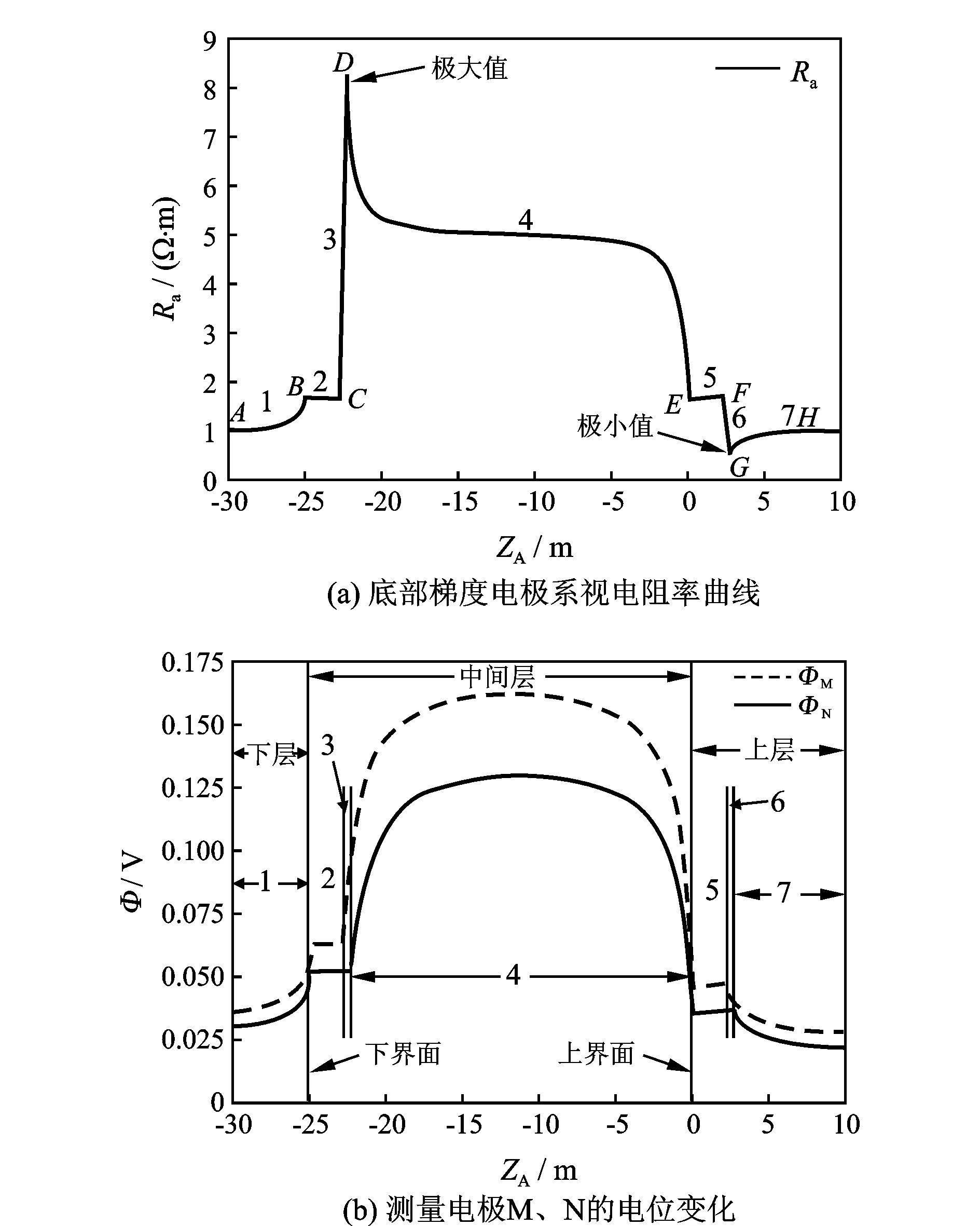
图3 用镜像法求出的解析解

3 数值仿真三层媒质中梯度电极系的测井响应

为验证上述结果的正确性，根据前述各参数，本文采用COMSOL多物理场有限元数值计算软件建立模型对底部梯度电极系的测井响应进行仿真。COMSOL多物理场有限元数值计算软件具有强大的网格剖分、求解器和丰富的后处理功能，且具有高效的计算性能，可提高数值仿真精确性。针对上述地层模型及恒定电流场的特点，在COMSOL中选用合适的物理模块和求解器进行求解，精确地计算梯度电极系中测量电极的电位，进而计算其视电阻率，分析梯度电极系的响应特点。计算结果如图4所示。

由图4可知，视电阻率的极大值出现在下底部，这也就是为什么称为底部梯度电极系的原因。视电阻率的极大值和极小值分别出现在整个电极系刚进入高阻层和整个电极系刚离开高阻层时，可以利用此特征点来划分高阻层厚。

比较图3和图4可知：

图4 数值计算底部梯度电极系视电阻率结果

(1)利用COMSOL软件数值计算的视电阻率变化趋势与解析解及文献[9]中的底部梯度电极系理论曲线一致，说明解析解的正确性与数值求解的可行性。若电极系远离高阻层，视电阻率曲线两端趋近于上下围岩电阻率；若电极系处于高阻层中间部分时，有一段视电阻率近似等于高阻层电阻率；若整个电极系刚进入高阻层和整个电极系刚离开高阻层时，视电阻率达到极大值和极小值。

(2)视电阻率取极大值和极小值时电极系的位置与解析解中的位置相同，据此可以划分高阻层的界面。

4 结 论

(1)研究三层导电媒质中的镜像法，建立了源点位于不同区域时任意区域的镜像源的位置、个数和大小，求解电位场的解析式。解析式揭示了三层导电媒质中点源建立恒定电流场形成电位的机理。

(2)应用三层导电媒质中的镜像原理计算三电极梯度电极系在三层地层中的测井响应，归纳总结出视电阻率与电位变化特征与电极系位置的关系。当三电极梯度电极系穿过三层地层时，测井响应特征与3个电极所处地层相关，电位场解析式与镜像源的关系揭示了梯度电极系的测井响应机理。

(3)用COMSOL多物理场有限元数值计算软件计算了底部梯度电极系的测井响应，验证了基于三层媒质镜像原理的电位推导公式及其大理石 电极梯度电极系测井响应特征的正确性。

(4)三层导电媒质中的镜像法和电位计算公式可用于分析普通电阻率测井中其他类型的电极系在不同导电媒质层中的响应特征， 为电极系参数设计提供理论依据。

[1] 张庚骥.电法测井[M].东营：石油大学出版社,1996:40-70.

[2] 王家映.石油电法勘探[M].北京:石油工业出版社,1921:4-12

[3] SHI Xiao-feng,LI Zheng,WANG Bao-fa,et al.Numerical evaluation of magnetic-dipole field in inclined multilayer dipping media[J].Journal of Beijing University of Aeronautics and Astronautics,2008，27(3):624-637.

[4] Vujevic Slavko,Sarajcev Petar.Potential distribution for a harmonic current point source in horizontally stratified multilayer medium[J].The International Journal for Computation and Mathematics in Electrical and Electronic Engineering,2008，27(3):624-637.

[5] 葛为中.层状介质点源电场正演解析及应用[J].地球物理学报，1994,37(1):534-541. GE Wei-zhong.The forward solution of the electrical field due to a point source in layered media and its applications[J].Chinese Journal of Geophysics,1994,37(1):534-541.

[6] 晁立东，仵杰，王仲奕.工程电磁场基础[M].西安:西北工业大学出版,2002:60.

[7] 陈聪，李定国，龚沈光.浅海中静电偶极子电场分布的镜像法研究[J].武汉理工大学学报：交通科学与工程版,2010,34(4):716-721. CHEN Cong,LI Ding-guo,Gong Shen-guang.Research on the electrical field produced by static electric dipole located in shallow sea with mirror image theory[J].Journal of Wuhan University of Technology：Transportation Science & Engineering,2010,34(4):716-721.

[8] 陈聪，李定国，蒋治国，等.二次等效法求三层媒质中静态电偶极子的场分布[J].物理学报,2012,61(24):1-6. CHEN Cong,LI Ding-guo,JIANG Zhi-guo,et al.Electric field of a static electric dipole in three-layer medium model using secondary equivalent method[J].Acta Physica Sinica,2012,61(24):1-6.

[9] 丁次乾.矿场地球物理[M].东营：石油大学出版社,2008:26-32.

[10] 郭飞.恒定电场边值问题中点源的处理[J].大学物理,1999,18(7):4-7. GUO Fei.The treatment of point source in boundary value problem of static electric field[J].College Physics,1999,18(7):4-7.

责任编辑：王 辉

2014-04-01

陕西省自然科学基础研究计划项目(编号：2013JM5011)；陕西省教育厅省级重点实验室重点科研计划项目(编号：12JS079)

仵杰(1965-)，男，教授，博士，主要从事电磁测井理论、仪器设计、数值模拟和阵列感应测井信号处理方面的研究。E-mail：wujie@xsyu.edu.cn

1673-064X(2015)01-0001-06

TE132

A