UPR100弧焊机器人轨迹规划

郑洁，赵慧，蒋林

(武汉科技大学机械自动化学院，湖北武汉 430081)

0 前言

机器人轨迹规划是在机器人运动学和动力学的基础上，根据机器人要完成的任务设计机器人各关节的运动规律，是机器人进行运动控制的基础［1］。轨迹规划的目标是得到理想的任务空间和运动空间轨迹，使机器人能够快速、准确、平稳的运动。机器人轨迹规划属于机器人底层规划，基本上不涉及人工智能问题［2］。

机器人运动学主要是把机器人相对于固定参考坐标系的运动作为时间的函数进行分析研究，而不考虑引起这些运动的力和力矩［3-4］。机器人运动学分析不仅是动力学分析的基础，而且为机器人的运动控制、离线编程、空间轨迹的规划提供了依据［5］。

本文作者以UPR100弧焊机器人作为研究对象，首先应用D-H参数法建立了焊接机器人的连杆坐标系，推导出正逆运动学公式;然后利用正、逆运动学进行轨迹规划;最后运用SimMechinics建立了UPR100弧焊机器人模型，并对仿真结果进行分析。

1 UPR100弧焊机器人连杆坐标系的建立

UPR100弧焊机器人的实体模型如图1所示，它的机械结构由腰部、大臂、小臂和手腕组成，共有6个关节，各关节均为转动关节，每个关节处都装有交流伺服电机，在机器人控制系统的作用下，驱动各个关节按照预定的空间轨迹运动，实现焊接功能。

图1 UPR100弧焊机器人外形图

机器人运动学分析的常用方法是D-H参数法。首先为UPR100弧焊机器人每个连杆指定一个本地的参考坐标系，建立在基座(连杆O)上的坐标系称为基座标系{O}，建立在连杆i上的坐标系称为坐标系{i}，因此对每个连杆都必须指定一个z轴和x轴，z轴总是与连杆的旋转轴重合，而x轴沿着公法线的方向由连杆i指向连杆i+1，y轴总是垂直于x轴和z轴的。采用D-H参数法建立了机器人连杆坐标系如图2所示，此时机器人悬臂和机械手与基座标系{O}的y0轴平行。

图2 UPR100弧焊机器人连杆坐标系

UPR100弧焊机器人的连杆参数如表1。

表1 UPR100弧焊机器人的连杆参数

表1中，变量θi，ai-1，αi-1，di(i=1，2，3，4，5，6)分别为各轴的转角、连杆的长度、相邻z轴之间的扭转角度以及相邻两轴最短距离。其中a1=155 mm，a2=590 mm，a3=180 mm，d4=606 mm。

2 UPR100弧焊机器人运动学

2．1 UPR100弧焊机器人正运动学

由连杆i相对连杆i-1相对位置的奇次变换矩阵可用i-1Ai来表述:

而机器人末端执行器相对基座标系的转换矩阵为:

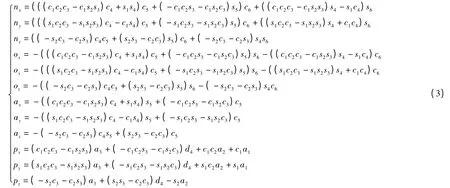
2．2 UPR100弧焊机器人逆运动学

已知末端连杆的位置和方位求得机器人各个关节变量θ1，θ2，θ3，θ4，θ5，θ6的值称为运动学逆解，采用解析法求得各关节角如式(4)所示:

UPR100弧焊机器人的运动学逆解可能有八组解，但由于结构限制，有些解不能实现。在存在多组解的情况下，通过Matlab编程实现了逆运动学求解及最优解的选择，以满足机器人的工作需求。

3 UPR100弧焊机器人轨迹规划

机器人轨迹规划是根据机器人要完成的任务设计机器人各关节的运动规律。它主要分为两种:关节空间轨迹规划和直角坐标空间轨迹规划［6］。由于弧焊机器人的工作轨迹是连续曲线，因此，宜采用直角空间的轨迹规划。

在直角空间内进行规划是指将手部位姿、速度和加速度表示为时间的函数，而相应的关节位移、速度和加速度由手部的信息导出。通常通过运动学逆解得到关节位移，用逆雅克比求得关节速度，用逆雅克比及其导数求得关节加速度［7］。

在直角空间进行轨迹规划的时候必须解决两个问题［8］:

(1)如何给出路径轨迹变化规律;

(2)如何利用关节变量变化规律来实现笛卡尔坐标空间的具体规划。

文中以螺旋线为例进行焊接机器人轨迹规划，设螺旋线的参数方程为:

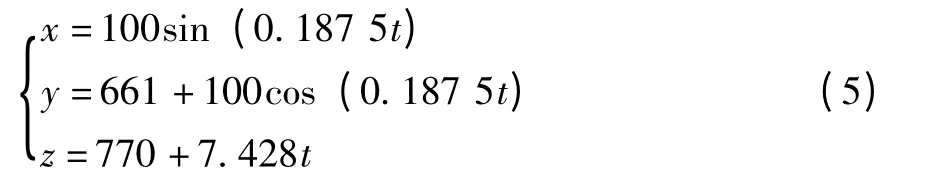
则当t∈［0，10］s时，焊接机器人末端理想轨迹如图3所示。

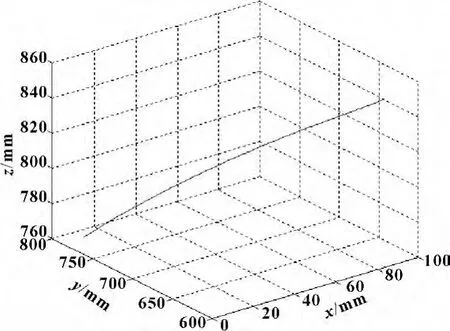
图3 焊接机器人末端理想轨迹

当t=0时，理论轨迹的初始点坐标为(0，761，770)，与机器人末端执行器的初始位置重合。焊接机器人焊接时，为保证焊接质量，焊接速度恒定，采用等时也即等距插补的方法进行轨迹规划。由式(3)可知，末端执行器的位置仅与θ1，θ2，θ3关节角有关，通过逆运动学、曲线拟合得到θ1，θ2，θ3对时间的函数如式(6)所示:

根据式(6)，θ1，θ2，θ3关节角随时间的变化曲线如图4所示。

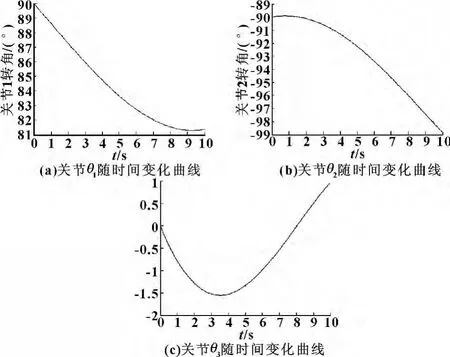
图4 θ1，θ2，θ3关节角随时间变化曲线

4 UPR100弧焊机器人轨迹规划仿真

UPR100弧焊机器人的6个关节均为转动关节，由前面可知UPR100弧焊机器人的初始状态如图2所示。

建模时需在机器人各关节模型上添加关节驱动器，并连上相应的关节传感器，组成机器人运动模型。机器人末端执行器的位置仅与θ1，θ2，θ3关节角有关，所以建模时仅给关节1、2、3添加关节驱动器。Simmechanics模型如图5所示。

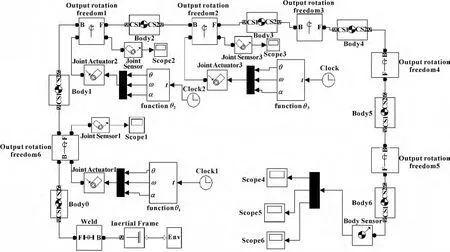
图5 UPR100弧焊机器人SimMechanics模型

轨迹规划开始时，机器人初始姿态如图6所示，末端执行器的初始位置与目标轨迹的初始点重合，由前面求得的各关节的初始角度为θ1=90°，θ2=-90°，θ3=θ4=θ5=θ6=0。

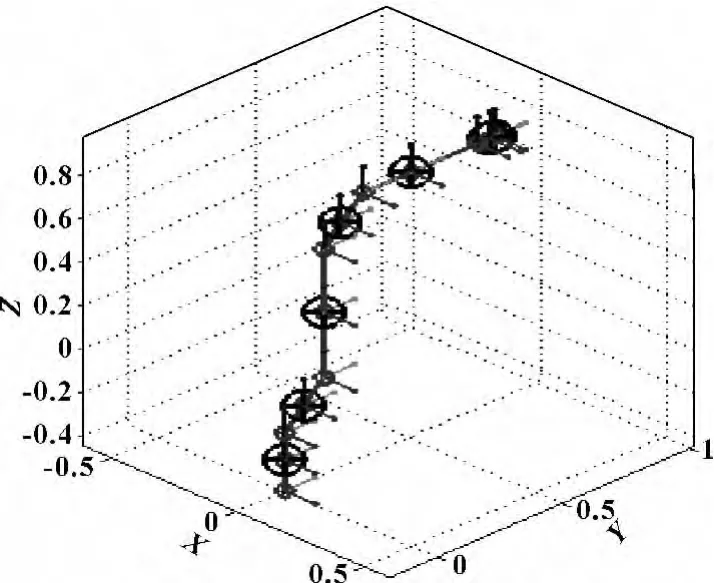
图6 UPR100弧焊机器人初始姿态

添加关节驱动后，轨迹规划结束时焊接机器人如图7所示。

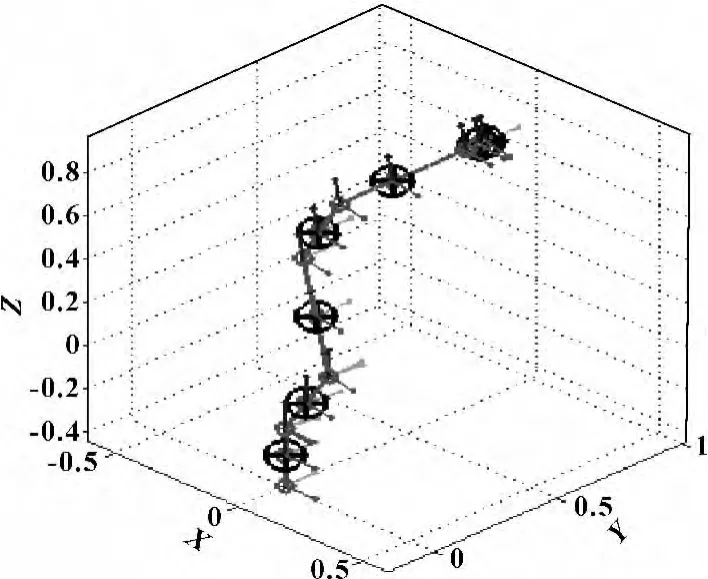
图7 轨迹规划结束时焊接机器人姿态

将机器人末端执行器的运动轨迹导入到工作空间，运用plot3指令进行绘图，结果如图8所示。

图8 UPR100弧焊机器人的末端轨迹

由于运动学正解具有唯一性，机器人的各个关节角度确定后，机器人末端轨迹是确定的。将焊接机器人末端轨迹与理论轨迹进行比较，最大的误差值为理论计算值的0．04%。因此，采用直角坐标空间进行轨迹规划是合理的，同时验证了第2节正逆运动学公式推导的正确性。

5 结论

以UPR100弧焊机器人作为研究对象，讨论了焊接机器人的坐标系建立、正逆运动学公式推导、轨迹规划及SimMechanics建模等问题，结论如下:

(1)采用D-H方法建立了机器人连杆坐标系，应用齐次变换矩阵建立运动学方程，采用Matlab编程实现了正逆运动学求;

(2)基于正逆运动学分析，在直角空间内对焊接机器人进行轨迹规划，为焊接机器人运动控制器设计提供了基础;

(3)通过SimMechinics对UPR100焊接机器人进行建模仿真，并把轨迹规划仿真数据与理论数据进行比较，结果验证了采用直角坐标空间进行轨迹规划的合理性以及正逆运动学公式推导的正确性。为焊接机器人的进一步动力学研究和轨迹跟踪控制器的设计提供了理论基础。

［1］FUMIYA Matsumoto，HIROAKI Yoshimura．Dynamics and Trajectory Planning of a Space Robot with Control of the Base Attitude［J］．IUTAM Symposium on Dynamics Modeling and Interaction Control in Virtual and Real Environments．IUTAM Bookseries，2011，30:35-43．

［2］宋婧．六自由度机器人的运动优化和轨迹规划算法研究［D］．武汉:武汉科技大学，2011．

［3］李庆玲，刘加亮．六自由度工业机器人运动学分析及仿真［J］．机电工程技术，2008，37(11):36-38．

［4］蔡自兴．机器人学［M］．北京:清华大学出版社，2000．

［5］J R，AGUILAR-NÁJERA C R．A Novel Six-degrees-of-freedom Series-parallel Manipulator［J］．Journal of Mechanical Science and Technology，2012，26(6):1901-1909．

［6］TADEJ Bajd，MATJAatjaŽMihelj，JADRAN Lenar C∨iC∨．Trajectory Planning Robotics Intelligent Systems［J］．Control and Automation:Science and Engineering，2010，43:67-75．

［7］LUIS Gracia，JOSEP Tornero．Optimal Trajectory Planning for Wheeled Mobile Robots Based on Kinematics Singularity［J］．Journal of Intelligent and Robotic Systems，2008，53(2):145-168．

［8］许志杰，王念峰，张宪民．六自由度涂胶机器人轨迹规划［C］．中国机构与机器科学应用国际会议(2013 CCAMMS)，2013:194-199．