6-SPS并联机构的运动学仿真与分析
李学明,周毅钧,徐海洋,谢赛南
(安徽理工大学机械工程学院,安徽淮南 232001)
0 前言
并联机器人由于结构新颖,近年在国内外得到广泛关注。6-SPS并联机构是一种典型的并联机构[1-2]。此类并联机构的正解方程是关于位置和姿态参数的高度耦合的非线性方程组,难以进行解析求解[3]。随着虚拟样机技术的发展和广泛应用,将并联机构的求解问题运用虚拟样机软件技术进行求解的方法日益普及。ADAMS是一款机械系统动力学分析软件,具有强大的建模、仿真分析、测量和数据处理能力。将并联机构的求解问题运用ADAMS软件来分析显得更简单和明了[4]。本文作者以6-SPS并联机构为研究对象,对其位置逆解和位置正解进行仿真,并对仿真结果进行了验证。为此类机构位置正解的求解与控制提供参考。
1 6-SPS并联机构虚拟样机的建立及运动学逆解仿真
1.1 6-SPS并联机构虚拟样机的建立
在SolidWorks中建立6-SPS并联机构的模型,其定平台是一个半径为1 000 mm的圆盘,在此底盘半径为850 mm的圆周上均布6个半球孔作为铰接位置。同样,其动平台是一个在半径为550 mm的圆周上均布6个半球孔的半径为700 mm的圆盘。两个平台之间的距离为1 000 mm,并且通过6根驱动杆相连。这里需要注意的一个地方是,确保定平台的中心是在SolidWorks里面的坐标原点,以便导入ADAMS里面之后,其坐标值是确定的。如图1所示。

图1 6-SPS并联机构模型
将建好的模型另存为Parasolid(*.x_t)格式后导入ADAMS中,对导入的模型添加材料属性。然后在6根驱动杆与动平台之间添加6个球副,与定平台之间添加6个球副,还有6根驱动杆之间也要添加6个移动副。
1.2 6-SPS并联机构的运动学逆解仿真
已知动平台的位置和姿态求解驱动杆的长度称为并联机构的逆解。6-SPS并联机构的运动学逆解仿真过程是[5]:在动平台的圆心处添加一个多自由度驱动,定义动平台圆心处的运动,单击Measure选项,测量驱动杆的位移曲线图。通过ADAMS的PostProcessor功能模块显示驱动杆的位移-时间曲线。最后把得到的驱动杆位移-时间曲线在PostProcessor模块中转换成样条曲线,到此完成了6-SPS并联机构运动学逆解的求解过程。将驱动添加在动平台的圆心(0,0,-1 000)处,对所加驱动进行编辑,包括Tra x、Tra y、Tra z方向的运动定义。ADAMS中的求解器模块其实质是一种求解的程序,是用来求解机构运动学和动力学问题的程序,在使用时输入机构的相关参数,就可以得到用户所需的计算结果。此6-SPS并联机构的仿真设置为:Tra x=60sin(0.85t);Tra y=60sin(0.3t);Tra z=70sin(0.2t)。其相关参数的设置为:End time为5 s,Steps为200步,然后对此机构进行运动仿真分析,得到6根驱动杆的长度随时间变化的曲线图。将所得的6幅曲线图综合放在一张图上,如图2所示。从图中可以看出,6根驱动杆在时间为0的时候长度相等,与模型的初始状态条件相吻合。
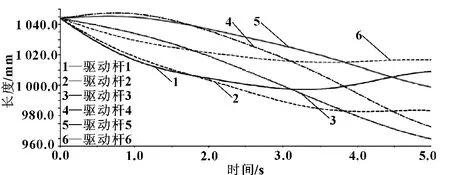
图2 驱动杆长度变化图
2 运动学逆解仿真结果与理论结果的对比
设Ai为动平台上6个铰接点的绝对坐标;Ci为动平台上6个铰接点在以自身圆心为坐标原点的相对坐标;Bi为定平台上6个铰接点的绝对坐标。记为[6-7]:
Ai=(xAiyAizAi)T
Ci=(xCiyCizCi)T
Bi=(xBiyBizBi)T
由于此6-SPS并联机构的虚拟样机模型已经在ADAMS里面建立完成,在后面的计算中若需要什么数值,通过测量可直接获取。已知动平台的姿态变换矩阵为[8]:

式中:α表示动平台绕x轴旋转的角度;
β表示动平台绕y轴旋转的角度;
γ表示动平台绕z轴旋转的角度。
此6-SPS并联机构中,α=0,β=0,γ=0。所以经计算,得:

经推导,可知:
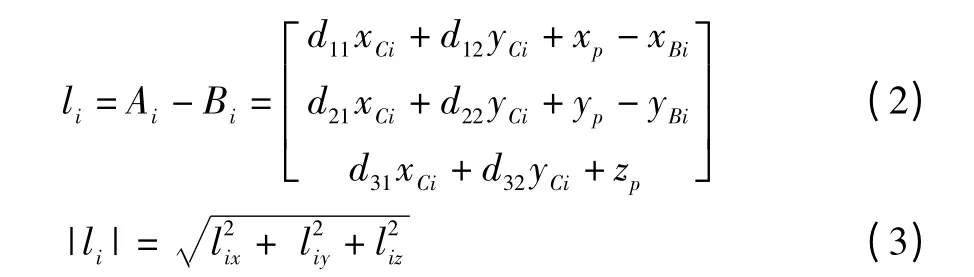
式中:xp=60sin(0.85t)
yp=60sin(0.3t)
zp=70sin(0.2t)-1 000
xCi,yCi,xBi,yBi的值均可在ADAMS中测出。
将所有值代入,可得:

既然l1已经被求解出来了,那么|l1|的值也就是l1对应的矩阵里面的3个元素先各自平方求和再开方。由于计算复杂,运用MATLAB对其进行计算。大体步骤是:将逆解公式输入MATLAB中,并把MATLAB中的求解数据保存成txt格式然后导出MATLAB,接着打开ADAMS的界面,单击菜单栏中的file-import对话框,在File Type的文本框中选择Test Data(*.*),再选择Create Splines单选框,将MATLAB中的数据以样条曲线的形式导入到ADAMS中。点击ADAMS的后处理模块(PostProcessor),将MATLAB中的数据所生成的曲线和ADAMS中所得到的驱动杆位移曲线放在一起进行比较,如图3—8所示。
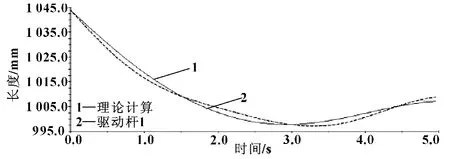
图3 驱动杆1的验证图

图4 驱动杆2的验证图
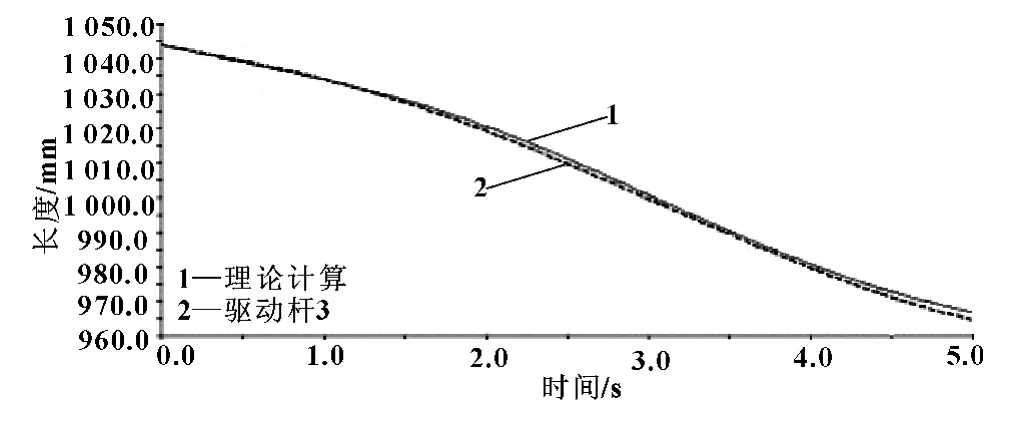
图5 驱动杆3的验证图

图6 驱动杆4的验证图
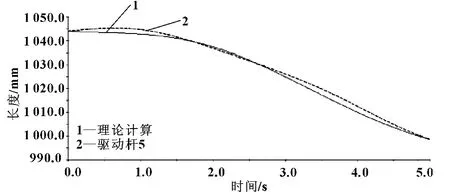
图7 驱动杆5的验证图

图8 驱动杆6的验证图
从图中可以看出,运用MATLAB计算出来的理论计算曲线与ADAMS的仿真曲线基本重合,验证了仿真位置逆解的正确性。
3 运动学正解的仿真与验证
6-SPS并联机构的正解仿真是根据已知6根驱动杆的位移状况来求解动平台的运动轨迹。首先将6根驱动杆的位移曲线在后处理模块中导出,点击菜单栏中的File-Export-Numeric,在Results Data对话框中右击选择Result_Component-Guess-*,把运动仿真所得的曲线以txt的格式保存起来。其中,第一列的值为各仿真点的时间,第二列的值为仿真点的伸长量。然后将txt格式的数据以样条曲线的形式转入ADAMS中,并分别以SPLINE_1、SPLINE_2、SPLINE_3、SPLINE_4、SPLINE_5、SPLINE_6命名,添加完成后可点击Tool-Database Navigator查看。
把动平台质心处的驱动撤销,在驱动杆的移动副上添加6个驱动,以Motion_1~Motion_6来命名,将样条曲线分别添加在6根驱动杆的移动副上,驱动杆的驱动函数类型设置为AKISPL(1st_Indep_Var,2nd_Indep_Var,Spline_Name,Deriv_Order),函数的具体参数设置如下:
AKISPL(time,0,Spline_1,0)
AKISPL(time,0,Spline_2,0)
AKISPL(time,0,Spline_3,0)
AKISPL(time,0,Spline_4,0)
AKISPL(time,0,Spline_5,0)
AKISPL(time,0,Spline_6,0)
最后,对仿真进行参数设置,由于采用的是并联机构逆解的样条曲线,所设置的仿真时间也为5s,仿真步数也设置为200步。测得动平台的仿真曲线,如图9所示。
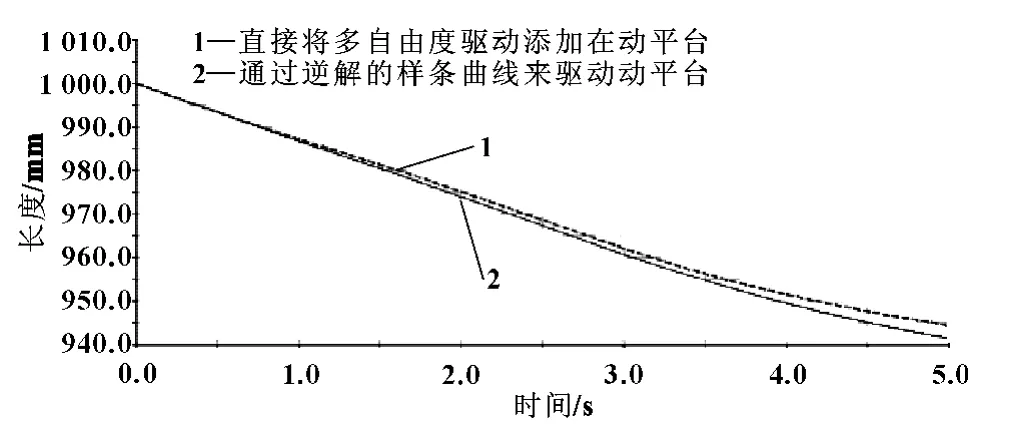
图9 动平台验证图
图中虚线代表的是直接将多自由度驱动添加在动平台上所测得曲线,实线是代表通过逆解的样条曲线来驱动动平台所测得的曲线。观察两条曲线,可以看出两者存在一定的误差,但是曲线的运动趋势以及方向高度吻合,说明利用ADAMS进行并联机构正解的运算是可行的且准确的。
4 结束语
介绍了利用ADAMS软件求解6-SPS并联机构的位置逆解和位置正解的详细过程,在得出了并联机构的逆解之后,运用MATLAB软件对并联机构进行了理论求解,与仿真结果进行对比,发现运动仿真结果与理论计算结果相吻合,证明了运用ADAMS对6-SPS并联机构的逆解和正解求解不仅具有较高的正确性,而且还可以提高求解的可视化程度,为6-SPS并联机构的位置求解与姿态控制提供参考。
[1]黄真,孔宪文.6-SPS并联机器人机构运动分析[J].东北重型机械学院学报,1992,16(4):283-287.
[2]FITZNERALD John M.Evaluating the Stewart Platform for Manufacturing[J].Robotics Today,1993,6(1):1-3.
[3]程世利.并联机构若干基本问题的研究[D].南京:南京航空航天大学,2011.
[4]范彩霞,刘宏昭.一种新型2T2R并联机构的运动学分析[J].机械科学与技术,2012,31(8):1253-1256.
[5]唐红品.基于虚拟样机技术的6-SPS并联机器人运动学和动力学的研究及参数优化[D].南京:南京理工大学,2011.
[6]卫进,毛昌明,寇子明.基于并联机构的新型液压支架的研究[J].矿山机械,2005,33(5):18-19.
[7]刘永均,张静,李柏林.基于条件数的3_RRS并联机器人运动性能优化[J].机械设计与研究,2008,24(6):32-34.
[8]张春林.高等机构学[M].2版.北京:北京理工大学出版社,2006.

