基于遗传算法的3-DOF并联机床机构的结构参数优化

张虎，郭志飞，张铮，徐安林

(1.无锡职业技术学院机械技术学院，江苏无锡 214121;2.江苏大学机械工程学院，江苏镇江 212013)

0 前言

并联机床具有结构紧凑、动态特性好、刚度大等优点，其中三自由度并联机床应用最为广泛［1－3］。并联机床机构的设计中，一般以机床的结构对称性、工作空间、灵活度、速度与承载能力等作为评价指标。依据机构学相关理论，机床结构参数(如杆长、机床床身尺寸)直接影响上述指标，因此在选型结束后，需要对机床结构参数的进行优化［4－6］。

要获得较大的工作空间、高灵活度等多个优化目标时，可将这一问题转化成多目标优化问题。遗传算法［7］非常适用于解决复杂非线性和多维空间最优解等问题，在计算科学、模式识别等方面有着广泛应用。

本文作者是在选定3-P-(2U-2S)这一并联机构构型后，以工作空间、运动特性作为评价指标，将机床床身半径R、连杆杆长L作为优化设计参数，应用遗传算法来实现3-P-(2U-2S)机床机构的优化设计。

1 并联机床机构基本特征介绍

并联机床机构结构简图如图1。移动副作为机床的驱动副，通过伺服电机驱动3个滑块沿导轨直线移动，进而带动动平台实现三自由度平动，从而改变激光光头的位置参数，与激光系统配合后，可实现三自由度平动激光加工(激光切割或焊接)。

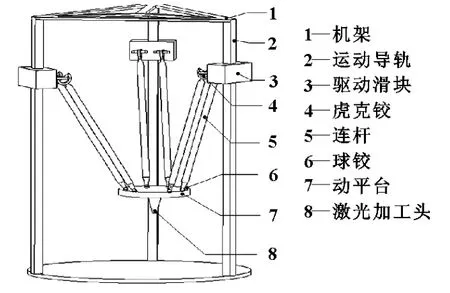
图1 机床结构简图

2 并联机床机构的位置方程

设定机架定平台OPi=R，O'Ai=r杆长为L，机床位置结构简图如图2所示。设定动平台中心O'在静坐标系O－XYZ下的坐标为(x，y，z)，各滑块点Bi在{O}坐标系内的坐标:

［Bi］o=(R cosαi-R sinαiZi)T

图2 机床位置结构简图

根据杆长约束方程可得到机床机构位置反解方程如下:

3 机床机构工作空间求解

并联机床的工作空间求解，通用的方法一般可分为几何解法和数值分析法。

数值分析法是根据约束条件(比如杆长约束、转角约束)，利用位置逆解来搜索边界和工作空间的内部点集的方法。该方法得到的工作空间是空间点的集合，一般是通过计算机计算获得，其优点在于程序化、可以通过改变相关参数，得到不同参数下的工作空间。取表1中的机床参数进行计算。

表1 机床结构参数

利用MATLAB计算得到工作空间和XOY方向投影的最大截面如图3。

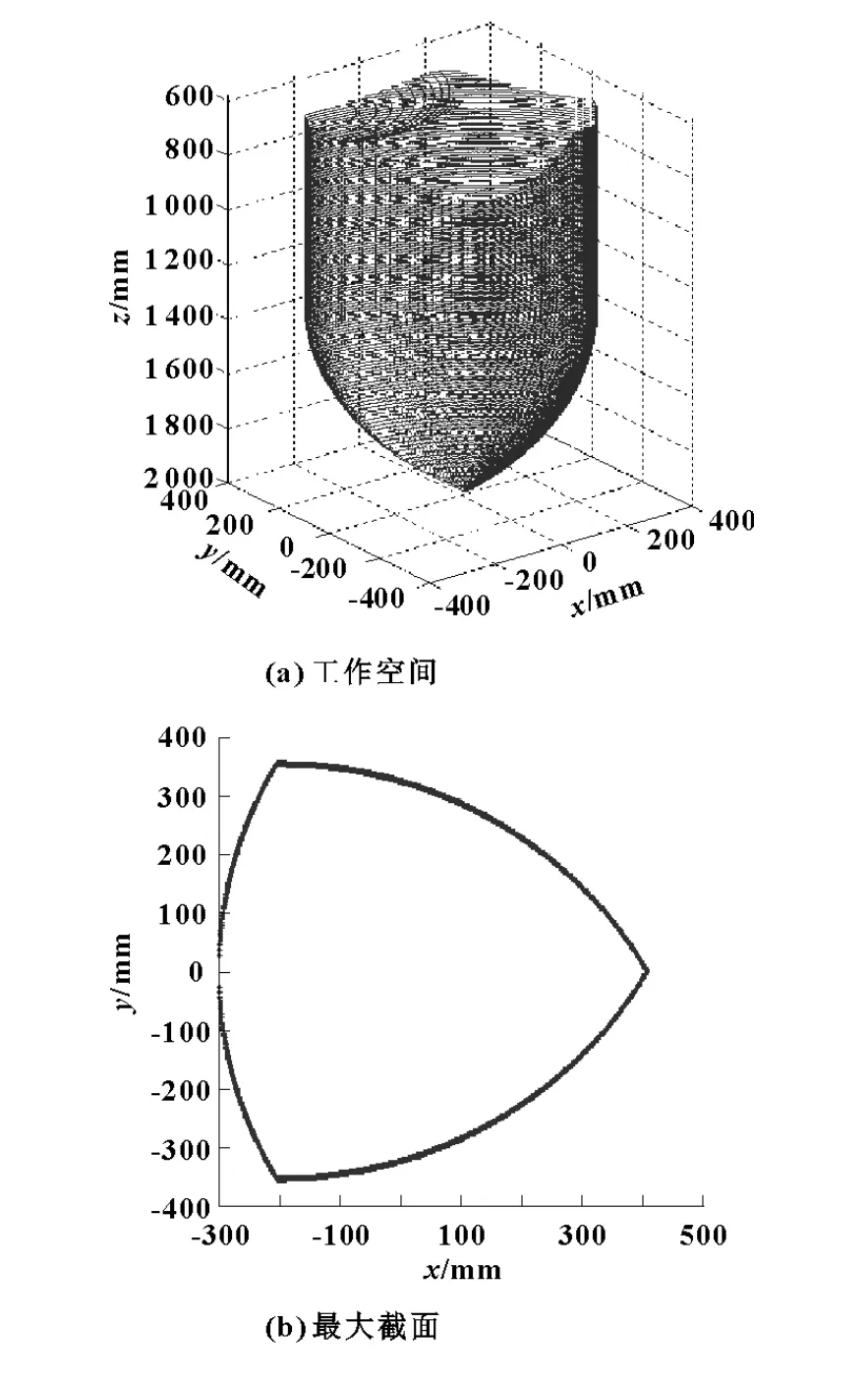
图3 并联机床工作空间与最大截面

同时，工作空间最大截面与机床结构参数的关系分析如下。

根据运动学原理，3个支链末端最大回转工作空间的交集，即为工作空间的最大截面如图4，3个圆的方程如下:

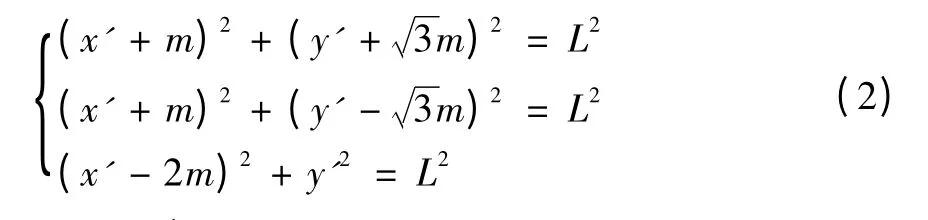
图4 工作空间最大截面

最大截面面积Smax，经计算可得:

导轨长度一定时，Smax与工作空间大小成正相关。

4 机床机构运动学特性求解

由于机床机构具有三平动自由度，输入与输出均为线速度。设定输入输出速度矢量分别为vin，vout，得Jvin=vout，雅克比矩阵J反映了机床滑块输入运动与动平台输出运动的映射关系。

由式(1)可得到雅克比矩阵J如下:

得到:

设定κ(J)=cond(J)=‖J‖·‖J－1‖称为雅克比矩阵条件数，反映了速度传递时的相对误差可能的放大率［8］。

条件数的倒数，η(J)=1/κ(J)，称为线速度传递各向同性(LCⅠ)，其值越大，则各项同性越好，速度传递性能在该点的传递性能越好，η(J)≤1，当η(J)=1，则各向同性处于最佳状态。

应用MATLAB软件求解η(J)=1/κ(J)，得到LCⅠ。图5是在LCⅠ在工作空间XOY面上的分布云图与等高线图。

从图5中可以直观地看出动平台在机床中心附近时，机床的LCⅠ较高，沿中心向外围扩散，即传递性能在机床机构中心最好，沿直径方向逐渐变差。在中心区域300 mm×300 mm(XOY平面)内LCⅠ值较大，同时中心点与边缘点的差值较小、分布均匀，说明机床加工工件时，运动的稳定性好。

另一方面，对于在规定工作空间W下的综合运动学性能，可通过全局条件指标GCⅠ来表示:

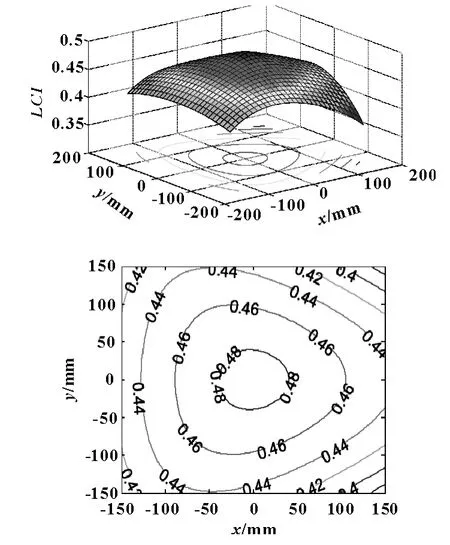
图5 LCⅠ在分布云图与等高线图(R=500，L=700)

5 基于遗传算法的机床机构参数优化

5.1 基本原理

遗传算法［9］基于自然进化规则搜索和计算问题，能够收敛得到全局最优解，基本操作包括选择、交叉和变异。BP神经网络算法有很强的映射能力，常常用于函数逼近、模式识别等。将遗传算法与BP网络算法结合，可以充分发挥神经网络的泛化的映射能力。通过BP网络算法构建目标函数模型，来作为遗传算法的寻优函数。

5.2 具体步骤

设定机床机构参数半径R、杆长L为变量，分别取范围为L∈［700，800］，R∈［500，600］(单位:mm)。

通过求解规定的工作空间(300 mm×300 mm×Z)的全局条件指标GCⅠ值，比较优化机床机构参数。通过求解可以到不同组合L、R得到的离散点(L，R，GCⅠ)，应用BP网络算法构建映射关系构造目标函数，因此GCⅠ作为机床机构运动特性的评价指标;另一方面，取工作空间最大截面Smax可以作为工作空间的评价指标。

将上述两种指标，构建评价函数通过“加权”的方式，来转换成单目标优化问题，通过遗传算法训练，得到一组工作空间与GCⅠ值较好的组合解，从而将多目标优化转换成单目标优化问题［97，104］，其数学模型如下:

其中ω1、ω2是赋给工作空间与GCⅠ的权值，f1、f2是参照满意度函数法［10］构造的对应于工作空间与GCⅠ的子函数，称为评估函数。由于两者均期望为最大值，函数定义的方法如下。

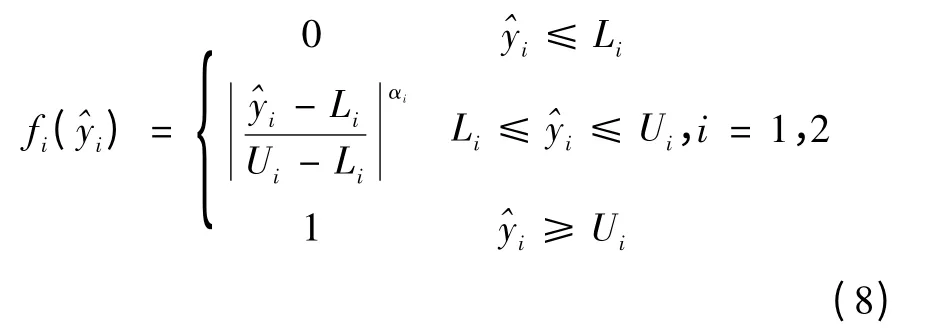
其中，是响应^yi是经GCⅠ或Smax得到的一个任意值，Ui对应最大值，Li对应最小值，αi是常数。这样经过上述数值转换后，工作空间与GCⅠ对应的的评估函数f1、f2的任意数值是fi(^yi)，其大小在一个数量级，从而不会使工作空间与GCⅠ本身数值大小影响优化效果。设权值与参数值ω1=ω2=1，α1=α2=1。

采用MATLAB遗传算法GAOT工具箱，作为求解最优值的求解工具。通过ga()相关语句，进行求优计算。经过100代的进化之后，得到最优值收敛于1.259 7。

5.3 优化结果

图6是GCⅠ与工作空间在遗传算法下的寻优性能跟踪图，图中虚线代表适应度函数的最佳值(Best fitness)和实线代表平均值(Mean fitness)。

最优参数值为:L=796.56;R=570.57

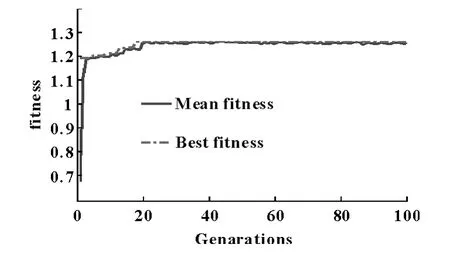
图6 遗传算法下的寻优性能跟踪图

将上述优化的机床机构参数尺寸代入到式(3)，求解得到优化后的工作空间最大截面，如图其面积为4.219 7e+005 mm2，优化后的LCⅠ在工作空间的分布如图8。

分析图3、5与图7、8，说明优化后机床机构在保证工作空间下，运动特性条件指标得到了提高，这样既能使并联机床在工作空间上满足加工要求，又能保证机床机构的运动学性能。综上，文中的机床机构的参数优化基本完成，优化结果令人满意。

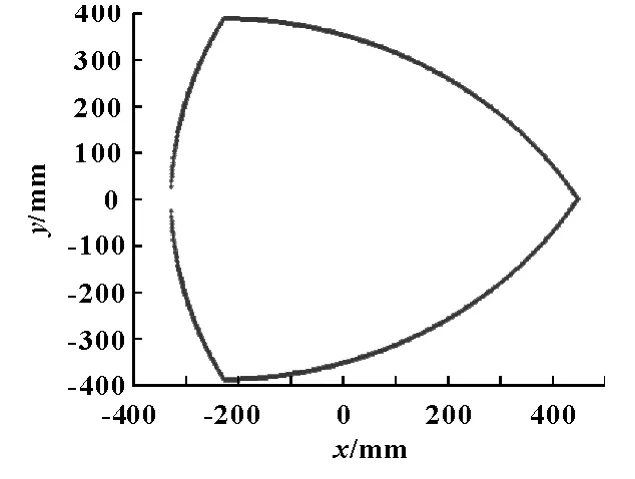
图7 优化后，最大工作空间截面图

图8 LCⅠ在优化后分布云图与等高线图

6 结论

通过计算给出了并联机床机构3-P-(2U-2S)的反解方程，应用边界搜索的方法得到机床机构的工作空间，接着通过雅克比矩阵的求解得到并联机床机构的条件数方程。最后，应用BP网络算法构建映射函数，通过遗传算法对机床机构的结构参数(机床半径R与杆长L)进行了尺寸优化。通过优化，并联机床在工作空间和全局运动条件指标GCⅠ两个综合性能得到了提高。

［1］张曙，HEISEL U．并联运动机床［M］．北京:机械工业出版社，2003．

［2］COMPANY O，PIERROT F．Modelling and Design Issues of a 3-axis Parallel Machine-tool Original［J］．Research ArticleMechanism and Machine Theory，2002，37(11):1325－1345．

［3］HUANGZ，LI QC．On the Type Synthesis of Lower-mobility Parallel Manipulators［C］．Proceedings of workshop on fundamental issues and future research directions for parallel mechanisms and manipulators．Canada:Quebec，2002．

［4］ALTUZARRA Oscar，PINTO C，SANDRU B，et al．Optimal Dimensioning for Parallel Manipulators:Workspace，Dexterity，and Energy［J］．Journal of Mechanical Design，2011(7):133－141．

［5］JAMWAL Prashant Kumar，XIE Shengquan，AW Kean C．Kinematic Design Optimization of a Parallel Ankle Rehabilitation Robot Using Modified Genetic Algorithm［J］．Robotics and Autonomous Systems，2009，57(10):1018－1027．

［6］STOCK Michael，MILLER Karol．Optimal Kinematic Design of Spatial Parallel Manipulators:Application to Linear Delta Robot［J］．ASME J，2003，125:292－301．

［7］高振．空间三自由度并联，混联机构构型、性能与若干应用研究［M］．合肥:中国科学技术大学，2009．

［8］于靖军，刘辛军，丁希仑，等．机器人机构学的数学基础［M］．北京:机械工业出版社，2008．

［9］王小平，曹立明．遗传算法—理论、应用与软件实现［M］．西安:西安交通大学出版社，2002．

［10］蒙哥马利．验设计与分析［M］．傅珏生，等译．北京:人民邮电出版社，2009．