名优茶并联采摘机器人的结构设计与工作空间分析
高凤,陈勇
(南京林业大学机械电子工程学院,江苏南京 210037)
0 前言
随着农村劳动力紧缺,采茶人工荒已经成为制约茶产业可持续发展的瓶颈。每年有30%~40%的春茶不能及时采摘。现有的采茶机基于切割式工作原理,工作效率高,但是对新梢与老叶没有选择性,只能用于大宗茶采摘,不能满足高档名优茶的采摘要求。本文作者创新性地集成主动机器视觉技术和并联机器人技术,研究具备新梢智能识别功能的名优茶采摘机器人。
并联机器人具有刚度大、误差小、速度快及精度高等优点,满足名优茶高速采摘和精准性的要求。采用闭链结构的并联采茶机器人,使名优采茶高效精准自动化采摘成为可能。目前,针对并联机器人的研究主要是运动学及动力学分析[1-2],奇异性分析[3]、优化设计[4]和工作空间分析[5-6]等。并联机器人各单链之间的运动干涉限制了工作空间大小,分析工作空间成为实现机器人设计指标的关键手段。
1 机器人结构设计
基于Delta机器人技术和茶叶采摘技术,设计了适用于机采茶园的名优茶并联采摘机器人,包括静平台、动平台、驱动臂、执行臂和末端执行器五个部分。静平台放置控制系统,减少了机器人转动惯量。动平台安装末端执行器,实现机器人有选择性地高速采摘。驱动臂和执行臂通过控制系统驱动末端执行器运动。每个执行臂由4个完全相同的球铰联接,始终保持平行四边形的运动特性。
图1是机器人的工作示意图。
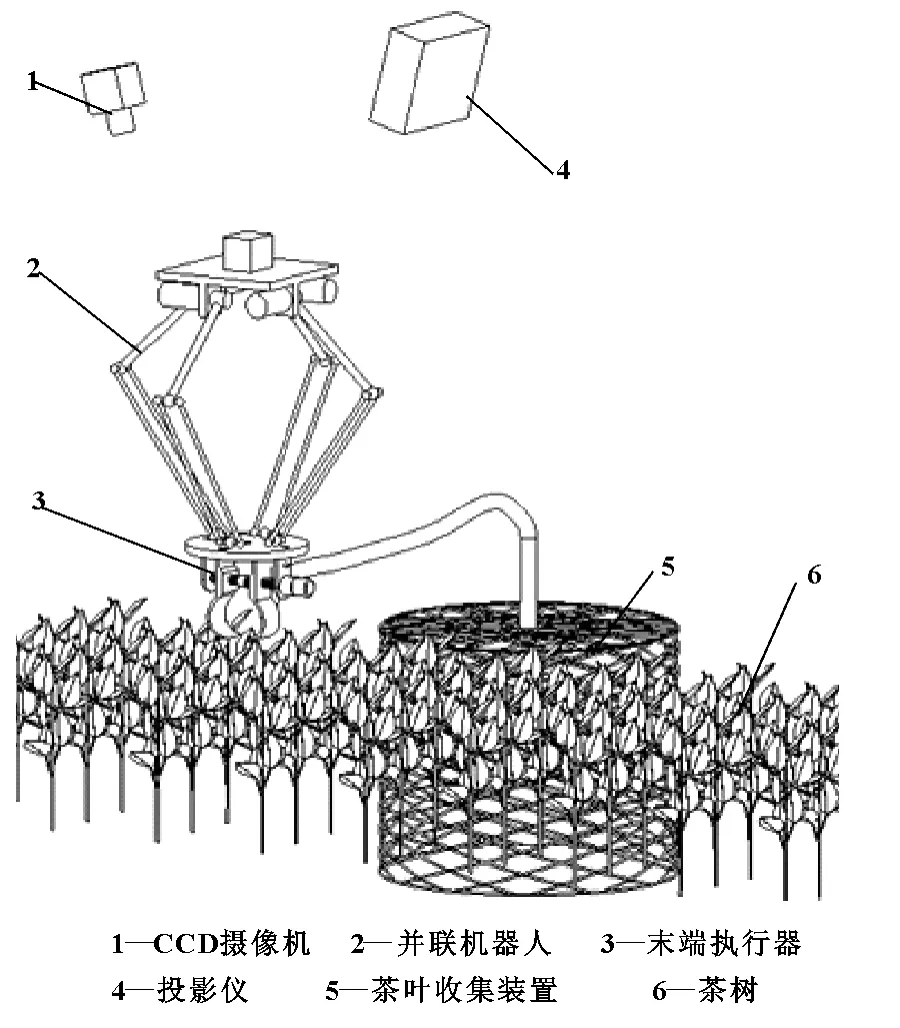
图1 机器人工作示意图
在该机器人采茶系统中,CCD摄像机1和投影仪4根据颜色特征和光栅投影技术实现新梢的识别、定位;控制系统驱动的并联机构2带动末端执行器3运动到新梢的空间位置,完成新梢的有选择性采摘。
1.1 并联机器人设计
由驱动臂和执行臂组成的并联机构,决定了机器人整体尺寸及茶叶采摘工作空间的大小。因此,必需进行名优茶并联采摘机器人尺度综合分析。即在给定机构灵巧度范围30°≤qi≤150°和杆件不发生干涉的前提下,利用GADS建立和求解给定工作空间的Delta机构几何设计变量的最优化问题,求出最优臂长。
对指定工作空间Delta机构的最优尺度综合定义如下[7]:
已知:指定工作空间体积W。
求解:工作空间包含W的Delta机构的几何参数。
假设目标函数F(Ⅰ)具有n个参数,则最优化问题可表示为:
min F(Ⅰ)
s.t.hi(Ⅰ,P)≤0表示所有的点P都在指定的W工作空间内。
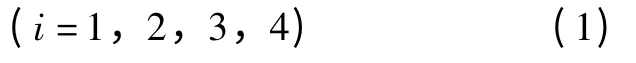
式中:Ⅰ=(x1,x2,…,xn)是未知的参数向量。每一个变量允许的变化范围xj=[xjmin,xjmax],(j=1,2,…,n)。其中最优解用Ⅰ*表示。
通过运动学逆解分析[8],求出问题的约束条件hi(Ⅰ,P),即
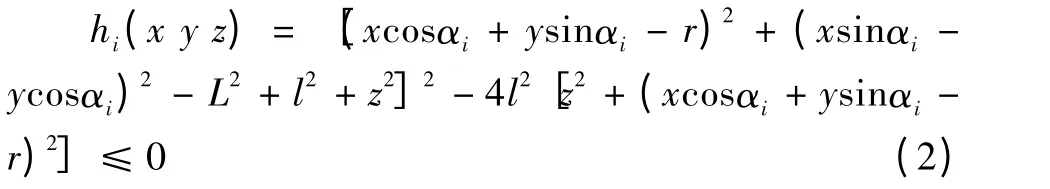
上述不等式(2)描述空间的一个体积,该体积的边界可由式hi(P)=hi(x y z)=0来确定。若用一系列特征点表示指定的工作空间W,当满足约束条件hi(Ⅰ,Pk)≤0(i=1,2,3,4,k=1,…,Npt)时,W包含在机器人的工作空间内。
其中l和L表示驱动臂和执行臂臂长,r表示单链一端点距离静平台中心与另一端点距离动平台中心的距离差,H表示指定工作空间到Delta机器人静平台的距离,角度αi描述四个电机的位置,Pi表示驱动臂在静平台上的安装位置。
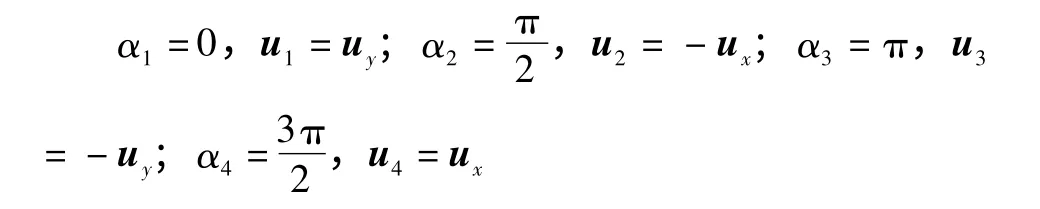
为了用于实验室的初次试验,设定一个较小的工作空间W为300 mm×300 mm×120 mm,如图2所示,其中Npt=8。要求设计的机器人工作空间必须包含W。新梢在竖直方向上的高度差小于100 mm。
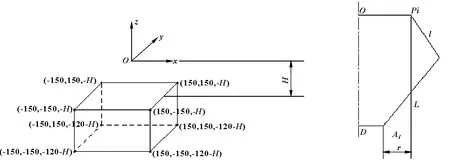
图2 给定的工作空间
将Pk代入式(2)中,未知量为L,l,r,H,可定义相互独立的设计变量为Ⅰ=[l,L,r,H]。计算Pk至曲面hi=0的距离,确定目标函数F(Ⅰ)。其中hi符号取决于Pk点相对于曲面的位置。因此,求解机器人尺度综合等价于寻找一个距离Pk点最近的曲面。
优化问题的约束条件为4个hi(Ⅰ,Pk)≤0(i=1,2,…4)的曲面,因此必须求出函数F(Ⅰ,Pk)=|h1(Ⅰ,Pk)|+|h2(Ⅰ,Pk)|+|h3(Ⅰ,Pk)|+|h4(Ⅰ,Pk)|的最小值,确定问题最优解。该函数可以看作是关于点Pk的权,那么,优化的最终目标是寻找一组最小设计变量Ⅰ*=[l,L,r,H],使得Delta机器人产生的工作空间包含指定的空间W。
1.2 GADS优化
运用GADS求解机器人的最优问题,优化工具箱中的主函数为:
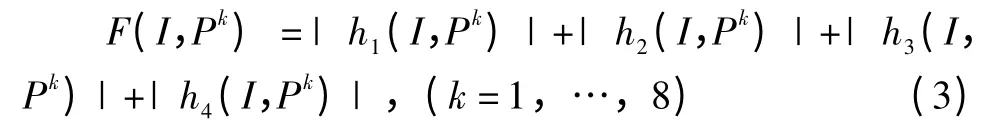
约束函数为:
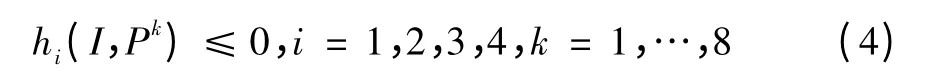
设定参数并运行,得到计算结果:L=273.077,l=220.871,r=40.279,H=244.203。
由于遗传算法初始种群的随机性,每次产生的个体距最佳个体的距离不同。为求解出最优结果,通过多次调试运行,确定最终臂长。调试结果如表1所示。
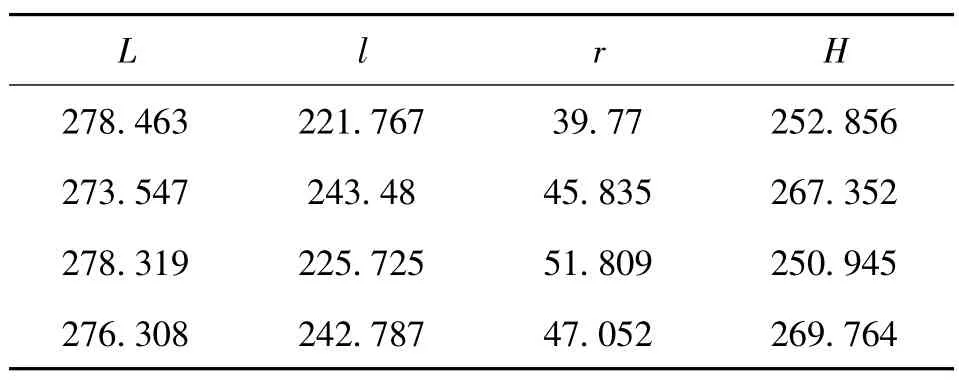
表1 MATLAB优化结果
通过多次优化计算,得出l=230 mm,L=275 mm,其中r=45 mm,H=260 mm。
2 工作空间分析
机器人工作空间是衡量机器人性能的重要指标[9]。根据并联机构的运动特性,机器人工作空间简化为四条完全相同的单链形成的四个包络体的交集。工作空间内的点必须满足以下两个条件[10]:
(1)逆解方程均需有实数解,即判别式Δi≥0,(i=1,2,3,4)。
(2)求解的关节转角qi有两组解,需至少有一组能满足相应的关节约束条件qmin≤qi≤qmax,(i=1,2,3,4)。
2.1 确定工作空间
利用雅克比矩阵计算得到的执行臂位置向量BiAi[8],根据BiAi=L建立约束方程:
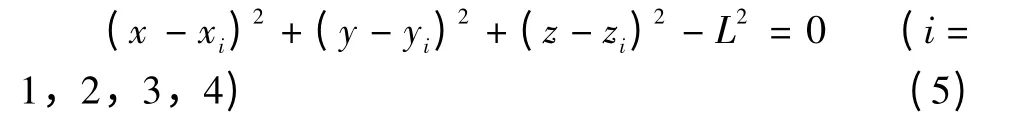
式中
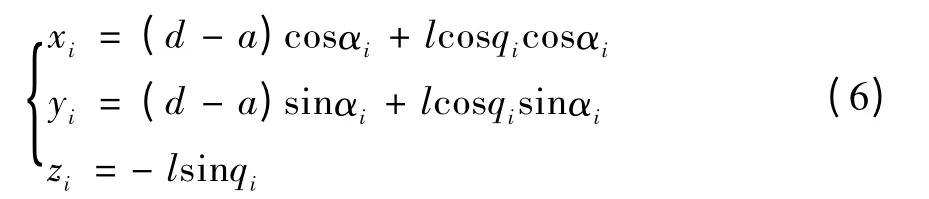
对于每一条单链,式(6)中qi为变量,a、d、l、αi、L为机构常量,所以式(6)表示为空间曲线的参数方程,记为R(qi)=(xi(qi),yi(qi),zi(qi))T。此处R(qi)表示垂直于xOy平面,圆心为Ni=(-(d-a)cosαi,-(d-a)sinαi,0)的圆。当qi在允许范围内变化时,R(qi)表示一段圆弧,记为π:R(qi)。
由式(5)可知,每条单链的工作空间表示为一个球面,球心位于(xi,yi,zi),半径为L。即工作空间为球心沿圆曲线连续移动形成的包络体,轴线过Ni点的一个圆环面。但由于受驱动转角范围的限制,圆曲线π不是一个整圆,按式(6)求出端点的位置坐标。因此,单链子空间为图3所示的一段圆环面,两端面为球心分别在Bi1,Bi2的半球面。
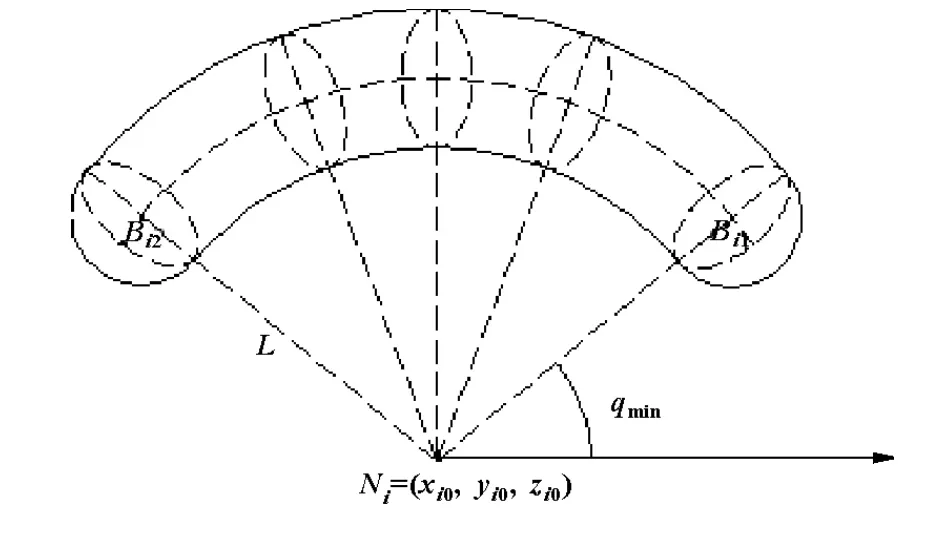
图3 单链工作空间
如果Bi1Bi2≥2l,则子空间内部没有空洞;如果Bi1Bi2≤2l,则子空间两边界球体相交,其交集{P(x,y,z),|P-Bi1|≤l}和{P(x,y,z),|P-Bi2|≤l}为动平台参考点不可到达的子空间区域,子空间内存在空洞,空洞边界为两球的相交部分[11]。根据给定驱动角的转动范围30°≤qi≤150°,通过几何计算得Bi1Bi2=476≥2l,即采茶机器人的工作空间中没有空洞。
2.2 工作空间极值计算
利用一系列平行于xOy的平面,将工作空间分割成厚度为Δz的微分子空间。鉴于并联机构的对称性,工作空间的最低截面z=zmin与最高截面z=zmax必然出现在x=0,y=0的位置。令x=0,y=0,对z轴方向进行一维搜索。
给定迭代初始值z0、z1,确保z1位于工作空间之内,z0位于工作空间之外。为确保z0绝对位于工作空间之外,将z0取得足够小。不断重复以下步骤,直到dz=z1-z0≤ε,ε为迭代精度。
令z=(z0+z1)/2,如果(x=0,y=0,z)为工作空间内的点,即满足机器人工作空间内的点要求的两个条件,取z1=z,否则取z0=z,由于每次迭代dz严格递减,搜索结果逐渐收敛于zmin。同理,求解zmax。
通过上述方法,利用MATLAB计算出zmin≈-503 mm、zmax≈-165 mm。
2.3 工作空间边界搜索
进行机器人工作空间边界搜索时,假设微分子空间为圆柱体。按照机器人工作空间内的点满足的约束条件,依次进行边界搜索。为保证搜索的精确性及完整性,起点z0应从比工作空间最低点zmin更低的位置开始,如图4所示。搜索完成后,再分析沿z轴方向增量为Δz的子空间,直到z=zmax为止。
子空间边界由图5所示的快速极坐标搜索法确定,工作空间内的点用极坐标表示。起始角由θ0开始,极径ρ0从0递增直至ρmax,当机构关节转角参数满足下列约束条件之一时,搜索停止并记录该极径ρ0。
qi1>q1max或qi1<q1min,qi2>q2max或qi2<q2min,qi3>q3max或qi3<q3min(i=1,2,3,4)。
以Δθ为增量,重复上述计算,完成微分子空间边界点的搜索,其体积可用式(7)计算。

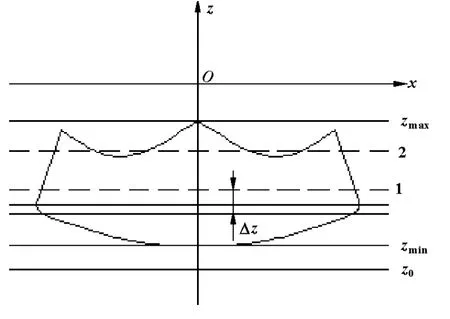
图4 工作空间微分子空间
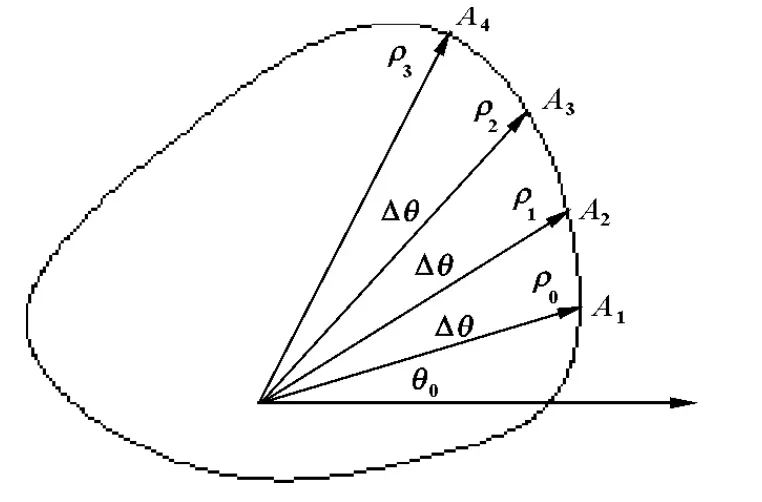
图5 工作空间极坐标搜索图
以Δz为增量,重复上述步骤,所求的机器人工作空间体积V等于各微分子空间的体积之和。
通过上述工作空间的计算,利用MATLAB中plot命令绘制图6所示空间三维图。

图6 名优茶并联采摘机器人工作空间
由图6可看出,名优茶并联采摘机器人的工作空间满足设计要求。以此为依据,制造了图7所示的机器人物理样机模型。

图7 机器人物理样机
3 结束语
完成了名优茶并联采摘机器人的结构设计,建立了机器人物理样机模型。在运动学逆解的基础上,采用GADS优化工具箱,确定了机器人臂长尺寸。结合数值法和几何法,利用快速极坐标搜索法计算出机器人工作空间的边界,并在MATLAB中绘制出三维图,验证了机器人满足设计的需求。
[1]STEFAN S.Inverse Dynamics of the 3-PRR Planar Parallel Robot[J].Robotics and Autonomous Systems,2009,57(5):556-563.
[2]刘宏伟,马质璞.3-RPS并联机构运动学分析及仿真[J].机械设计与制造,2012,50(1):211-213.
[3]HORIN PB,SHOHAM M.A Class of Parallel Robots Practically Free of Parallel Singularities[J].Journal of Mechanical Design,2008,130(5):052303-052311.
[4]王冰,陈久川.平面并联平动机器人尺寸设计研究[J].机床与液压,2007,35(9):37-41.
[5]ALTUZARRA O,AGINAGA J,HERNANDEZ A,et al.Workspace Analysis of Positioning Discontinuities Due to Clearances in Parallel Manipulators[J].Mechanism and Machine Theory,2011,46(5):577-592.
[6]尹小琴,马履中.三平移并联机构3-RRC的工作空间分析[J].中国机械工程,2003,14(18):1531-1533.
[7]LARIBI M A,ROMDHANE L,ZEGHLOUL S.Analysis and Dimensional Synthesis of the DELTA Robot for a Prescribed Workspace[J].Mechanism and Machine Theory,2007,42(7):859-870.
[8]高凤.名优茶并联采摘机器人结构设计与仿真[D].南京:南京林业大学,2013.
[9]KUMAR V.Characterization of Workspaces of Parallel Manipulators[J].Journal of Mechanical Design,1992,114(3):368-375.
[10]许敏.改进的Delta型并联机器人机构运动性能研究[D].沈阳:东北大学,2007.
[11]王霄,韩亚峰,林跃强,等.Delta型并联运动激光切割机床的工作空间分析[J].农业机械学报,2007,38(1):154-157,126.

