真空管道水力特性试验研究

张小莹，李 琳，王梦婷，谭义海

(1.新疆农业大学水利与土木工程学院，新疆 乌鲁木齐 830052;2.新疆新能源新风投资开发有限公司，新疆 乌鲁木齐 830000)

0 引言

目前，虹吸式输水管道已被广泛应用于实际工程中［1-5］。朱红耕等［6-7］运用三维数值模拟的方法，对虹吸管路的水力特性进行模拟分析，创造了虹吸管道研究的新篇章。目前，国内外学者多以短距离虹吸管道(如驼峰式虹吸管道)为研究对象，对虹吸的过程以及虹吸管道水力特性进行了多方面研究，但对长距离虹吸管道的研究较少。李琳［8］、许史［9-10］针对新疆台兰河某地下水库中的长距离虹吸管道进行了水力学模型试验，并发现随着安装高度的增大，管内的汽化现象愈发严重，虹吸管内由单一液相流转变成气液两相流;王梦婷［11］针对非驼峰式的正虹吸管道进行了系列试验研究，并将量纲分析法与数值拟合方法相结合，得出了计算长距离虹吸管道流量的公式。笔者在前期研究的基础上进一步探究了安装高度和上下游水位差与流量减小率的关系，通过对管道内气液两相流流型的研究，利用面积减小率对不同流型时流量的变化规律进行了分析。

1 试验装置及试验方案

1.1 试验装置及仪器

试验由上游进口溢流堰、虹吸管路、下游出口堰组成，试验装置如图1所示。其中，虹吸管路是由有机玻璃制作而成，管径2 cm，管长17.7 m，整个试验中管道相互连接处均为密封状态。在虹吸管道的上、下行管段的上部各安装一个环形掺气电极和压力传感器，下部各安装一个环形掺气电极和电子真空压力表，分别用以测量管道内掺气浓度和压强的大小，在水平管段从上游至下游依次布置5个环形掺气电极，水平管段开头及结尾处各安装一个压力传感器。

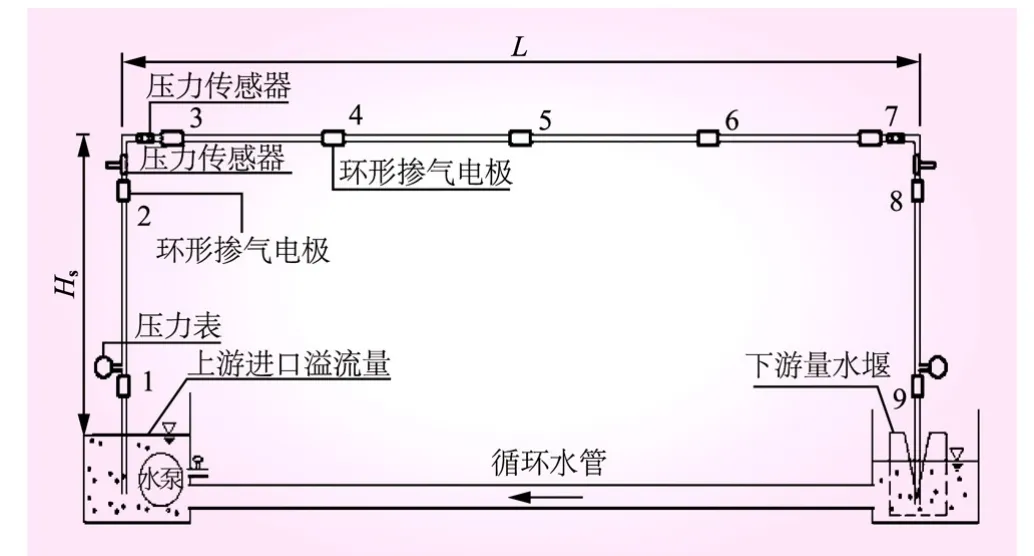
图1 试验装置示意

1.2 试验方案

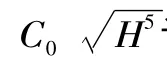
2 试验现象

试验观测了不同安装高度的管内流动状态，如图2所示。在1 m的安装高度下，管内水流为单一的液相流，管路完全被水充满，未观察到有气泡析出(图2a);当安装高度为2、3 m时，虹吸管道内有少量微小气泡析出，并且气泡随水流方向运动(图2b、图2c)，此时虹吸管道内的气泡分散在管道内随水流运动，这种流型为气泡流;当安装高度为4、5 m时，可以清晰地看到气泡的数量增多，并且气泡顺着水流方向运动(图2d、图2e)，个别小气泡集聚成的大气泡在管道顶部向下游运动;当安装高度为6 m时，管道内小气泡集聚成一个个大气泡沿着管道顶部运动(图2f)，此时管道内气泡数量明显减少，气泡间距增大，气泡之间掺混着一些小气泡，这种流型为气团流;当安装高度为7 m时，气团流的现象更为明显(图2g)，比6 m安装高度下气泡增大了1倍左右;当安装高度为8 m时，管段内仍然为气团流，气泡进一步增大，气泡随水流运动中发展为大气囊，当气囊体积增大到贯穿整个管段时，管路发生了断流现象(图2h)。

图2 安装高度为1～8 m工况下的试验现象

3 试验结果及分析

3.1 试验结果

表1为不同水位差下安装高度与流量关系，可看出:在上下游水位差不变的情况下，安装高度与过流量成反比关系;在安装高度一定的情况下，上下游水位差与过流量成正比关系。通过流量减小率研究安装高度对流量的影响程度，流量减小率ΔQ的计算公式为

式中，QL为管道输水流量的理论值，将hs=1 m时所测得的流量值作为管道输水流量的理论值;QS为不同安装高度下所测得的虹吸管的实际输水流量。

从式(1)可知:流量减小率越大，虹吸管道内实测流量值越小。由式(1)计算得到的结果如图3所示，在上、下游水位差不变时，hs越高，ΔQ越大，且ΔQ增加的程度较大;在安装高度一定的情况下，ΔQ随着上下游水位差的增大而减小。由此可知，虹吸管道的安装高度和上下游水位差这两个因素对虹吸管道内输水流量影响较大，而安装高度和上下游水位差不同时，虹吸管道内流态也不一样，管道内由单一液相流变为气液两相流，又可把气液两相流分为气泡流和气团流，且当管道内出现气泡流和气团流时，所测得的流量均小于满管时的流量。故笔者认为由于流型不同，管道内流量变化规律也不相同，因此下文分别对不同流型下管内的流量变化进行分析。

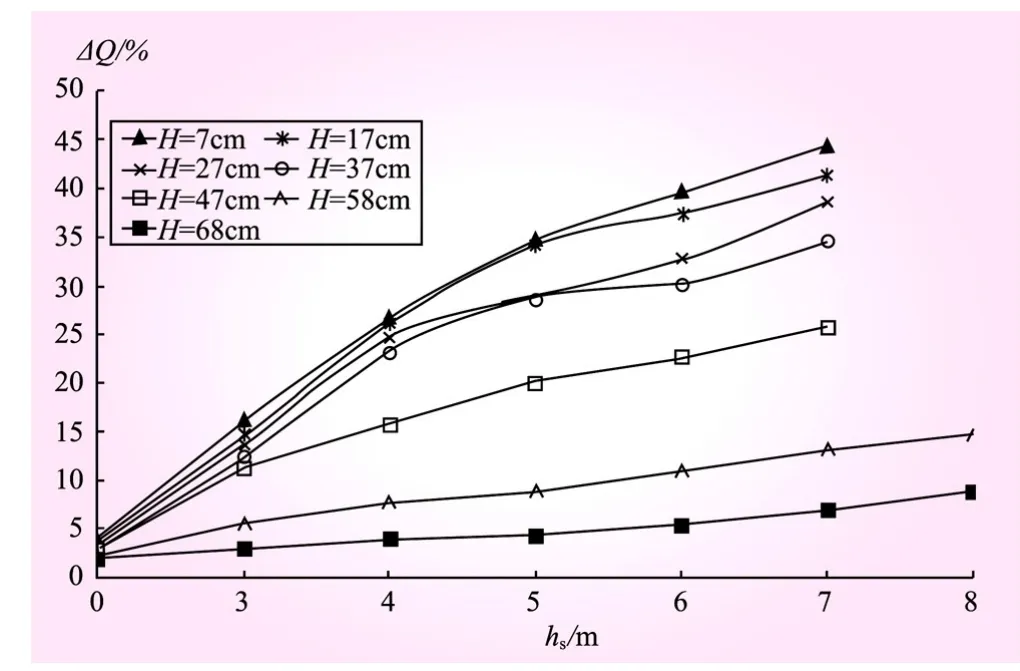
图3 不同安装高度hs与流量减小率ΔQ关系曲线

3.2 气泡流对流量的影响

常规有压管流流量计算公式为

式中，μ0为管道的流量系数;A为管道的过水断面面积。

根据表1可知，H一定情况下，随着hs的增大，虹吸管内的实测流量QS小于满管时的流量QL，流量减小的主要原因是流量系数或过水断面面积减小了。为此，引入面积减小率ΔA，即

式中，AL为虹吸管满管过流时过水断面面积;AS为实测的过水断面面积。

把试验所测数据带入式(3)得到结果见表2，由表2可知，当hs=2 m时，随着H的增大，ΔA逐渐减小，而ΔQ随着ΔA的减小而减小。ΔA与ΔQ的关系见图4a，可知ΔA与ΔQ呈线性关系，直线斜率约为1。即，当管道内流型为气泡流时，过水断面面积对管道流量的大小起决定性作用。

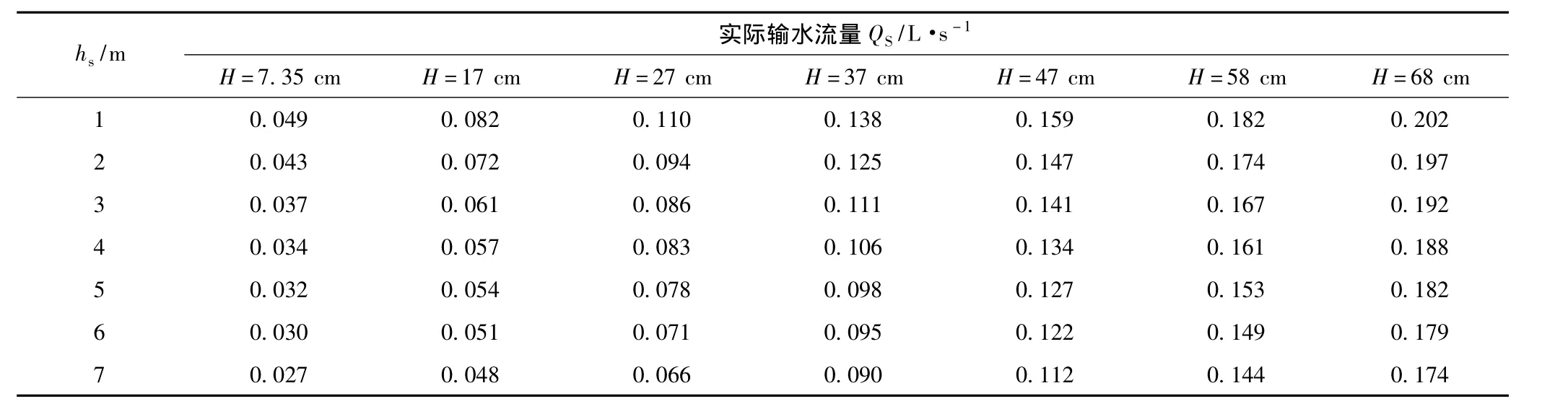
表1 不同水位差下安装高度与输水流量关系实测值

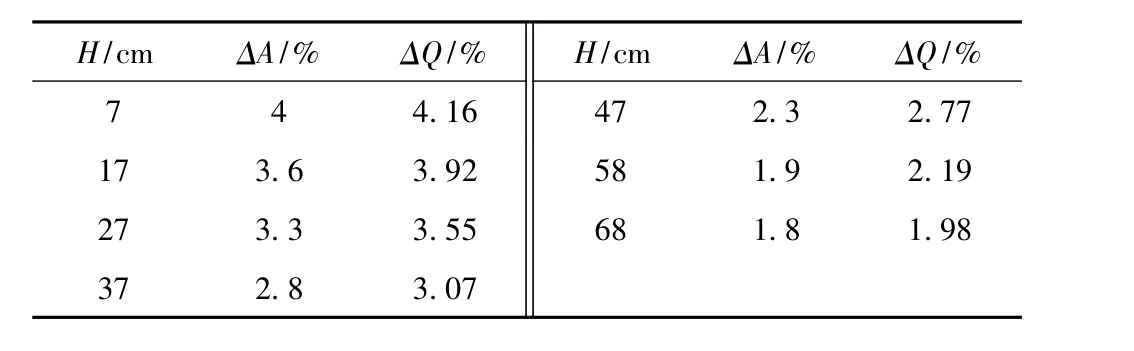
表2 hs=2 m时，不同上下游水位差下ΔA与ΔQ关系

3.3 气团流对流量的影响

当hs从4 m增大到5 m的过程中，虹吸管内为气泡流掺杂气团流，以气泡流为主。当hs从6 m增大到8 m时，真空管道内为气团流。将hs=7 m时不同上下游水位差下ΔA与ΔQ进行比较，如表3所示，可知，随着H的增大，ΔQ逐渐减小，ΔA也逐渐减小，但ΔQ的数值比ΔA大了两倍之余，ΔA与ΔQ的关系见图4b所示。故在以气团流为主的虹吸管道内，ΔA与ΔQ有关，故管道过水断面面积减小是引起流量减小的一个原因，除此之外，流量的减小应该还与其他因素有关。根据式(2)可知，当管道内为气团流时，流量系数的变化也是引起流量减小的主要因素。因此，流量减小还应考虑流量系数的变化，影响管道流量系数因素有很多，如沿程阻力系数、流速及局部阻力系数等，且真空管道水流掺气后对流量系数也会产生一定影响。故在后续试验研究中，应考虑掺气后的气团流中流量系数的变化规律。

图4 ΔA与ΔQ的关系

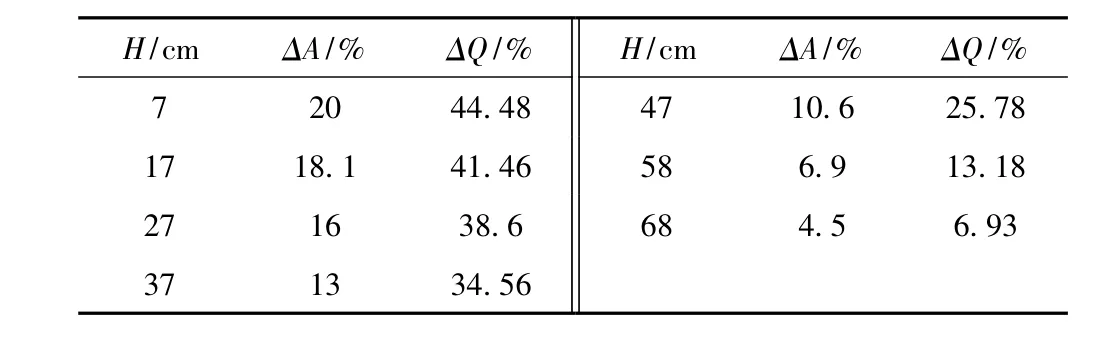
表3 hs=7 m时，不同上下游水位差下ΔQ与ΔA关系

4 结语

通过真空管道进行的系列试验研究，观察了不同工况下的水流流态，分析了不同安装高度及水位差下流量的变化规律，并得到以下结论:

(1)随着安装高度的增加，真空有压管内由单一的液相流变为气液两相流，且随着hs的增大，虹吸管内的气液两相流流型由气泡流→气泡流为主(掺杂气团流)→气团流为主(气泡流很少)→断流。

(2)真空有压管道的过流量随安装高度的增大而减小，随上下游水位差的增大而增大。且流量的变化与管道内的流型有关:当管道内为气泡流时，气泡流的面积减小率与流量减小率几乎相等;当管内为气团流为主时，气团流的面积减小率约占流量减小率的50%。

［1］李云，黄光明.老虎山水电站倒虹吸管伸缩节振动机理分析［J］.水力发电，2004，30(2):66-68.

［2］杨禧.昆明掌鸠河引水供水工程岔河倒虹吸设计［J］.水力发电，2010，36(10):38-41.

［3］张法思，朱建和.虹吸式进水口水电站机组甩负荷飞逸过渡过程分析［J］.水力发电，1990(5):50-52+37.

［4］冯新民.采用虹吸进水方式的小水电站［J］.水力发电，1983(6):45-46.

［5］洪庆松.虹吸管在城市取水工程中的应用［J］.有色冶金设计与研究，2014，35(5):89-91.

［6］朱红耕，袁寿其，施卫东，等.大型泵站虹吸式出水流道水力特性分析［J］.中国农村水利水电，2005(7):71-74.

［7］朱红耕.大型泵站虹吸式出水流道水力特性分析［J］.中国给水排水，2006，22(6):54-57.

［8］李琳，邱秀云，许史，等.长距离虹吸管道输水水力学模型试验研究［J］.南水北调与水利科技，2010，8(3):106-109.

［9］许史，李琳，邱秀云，等.长距离虹吸管输水试验研究初探［J］.中国农村水利水电，2010(3):70-72.

［10］许史.长距离虹吸管输水试验研究［D］.乌鲁木齐:新疆农业大学，2010.

［11］王梦婷，李琳.正虹吸管道水力特性试验研究［J］.水电能源科学，2014，32(12):87-90.