基于可靠度理论的岩质边坡经济风险评价

高 策，陈建康，吴震宇，周正军，王 滔

(四川大学水利水电学院，四川 成都 610065)

0 引言

岩质边坡稳定与边坡破坏模式、所处位置、破坏方量密切相关。在边坡实际开挖中，断层出露、人工扰动等因素对边坡稳定的影响较大。目前，评价边坡稳定主要有2种方法，一种是基于安全系数的评价方法，这种方法虽然有统一的评价标准，但安全系数人为给定，且把不确定荷载、岩土参数等作为确定量考虑，这显然是不符合实际的;另一种是基于可靠度理论的评价方法，该方法把影响边坡稳定的各种因素作为随机变量考虑，以概率论与数理统计为基础，计算边坡的可靠度指标和失效概率。如H.S.B.Duzgun等［1］研究了基于可靠度理论的岩质边坡平面滑动破坏时的设计方法;B.K.Low［2-3］提出了基于Excel的可靠指标计算的新算法;R.Jimenez-Rodriguez等［4］采用不相交的割集模拟岩质边坡平面滑动的体系可靠度问题;张兴、廖国华［5］采用蒙特卡罗方法计算了多滑面边坡的体系可靠度;谭晓慧等［6］以增量切线刚度法为基础，推导了基于修正的Aitken加速法的非线性随机有限元加速迭代公式，并将其应用于边坡稳定的可靠度分析中;吴震宇等［7］采用Ditlevsen窄界限公式估算了岩质边坡各失稳模式组成的串联体系的可靠指标;李典庆等［8］提出了基于n维等效方法的岩质边坡楔体稳定体系可靠度分析方法。

尽管可靠度理论在岩质边坡稳定研究中已取得了一些进展，但由于没有形成以可靠度分析为基础的规范，缺乏统一的评价标准，且计算出来的可靠度和失效概率无法对边坡的失稳风险进行直观的评价。因此，寻找一个可以把风险量化的指标成为风险评价的首要问题。王伟等［9］以经济作为风险评价指标，基于投资最省原则，确定边坡可接受的可靠性指标或破坏概率，从而判定边坡的稳定性;田斌等［10］以经济风险分析为基础，对岩质高边坡加固方案进行分析;曾晟等［11］提出基于可靠度的圆弧滑动边坡经济风险分析模型优化方法。本文在此基础上，以某工程边坡为例，建立了岩质边坡风险损失与支护量之间的关系，基于风险损失最小的原则，确定了该岩质边坡较为合理的支护方案。

1 边坡支护的经济风险分析流程

1.1 支护条件下边坡失效概率的计算

采用非线性有限元计算，通过逐步降低岩土体强度参数寻找潜在的滑移通道，并认为滑移通道上所有单元失效时边坡即失稳。因此，有几条滑移通道就有几种失稳模式。假设有m种失效模式，第n个失效模式下有j个单元，依据Druker-Prager屈服准则构建单元的功能函数，定义第n个失效模式下第i个单元表示为，则功能函数为

由于式(1)中含有不能显式表达的应力项，采用不含交叉项的二次多项式构建单元功能函数的响应面方程为

根据有限元计算和回归分析得出待定参数后，就可以采用蒙特卡洛随机抽样法计算单元的失效概率和相关系数。当破坏通道上的所有单元都失效时，认为边坡破坏失稳。因此，单一模式下失效概率可按并联体系进行计算，采用PNET法［12］近似计算并联体系的失效概率。在评价边坡整体稳定性时，由于存在多种滑移通道，每一条滑移通道失稳，则边坡整体失稳。因此，在求得各失稳模式的失效概率后，计算各失稳模式间的相关系数，最后按Ditlevsen［13］窄界限公式估算各失稳模式组成的串联体系的失效概率。

1.2 风险分析流程

在风险分析中，考虑资金的时间价值时通常可从静态和动态角度考虑。边坡工程开挖过程通常为人为活动，实施周期较短，为简化分析流程，可从静态的角度进行分析。常规的边坡稳定计算仅从保证边坡安全的角度出发，难以量化地评价边坡支护成本及风险损失之间的关系。边坡风险损失可由边坡失稳概率Pf和损失c这2个因素组成的函数表示，即

式中，R为边坡灾害活动的风险损失;Pf为边坡发生灾害活动的概率;c为边坡灾害活动产生的损失后果。

用边坡的经济指标来评价边坡的风险，采用费用值来表示边坡可靠性的影响效应。边坡开挖的总费用Cs可表示为

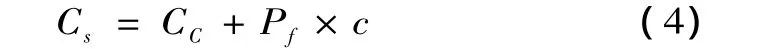
式中，CC为边坡开挖和加固费用。

按照经济风险评价的基本理念，对岩质边坡的失稳风险及其支护效果进行分析和评价:

(1)根据边坡的实际情况，先利用刚体极限平衡法对边坡进行稳定计算，判定目标边坡的稳定性，拟定必要的边坡稳定处理措施(如削坡、锚固等)。

(2)确定处理措施的控制变量。对削坡选取削坡高度、削坡角度作为控制变量;对锚固措施可将锚固数量、锚索吨位等作为控制变量。

(3)根据具体处理措施确定成本Cc，在相应的处理措施下对边坡进行可靠度分析，可以得到相应的Pf。根据最危险滑面的位置可以计算出滑体方量，从而间接得出滑动后造成的风险损失数额c。

(4)将Cc，Pf和c代入公式(4)，计算得到不同处理措施下边坡开挖的总费用Cs，每种处理措施即可算出一个与之对应总成本，由此得到边坡开挖总费用Cs和不同处理措施控制变量之间的关系曲线。若Cs值始终随控制变量的变化而增大，则说明边坡不需要治理或该治理措施效果不佳，不宜采用;若曲线具有极小值的拐点，则该极小值对应的边坡破坏概率为边坡可接受的破坏概率值，由此可得到对应的可靠性指标，此时的处理措施可作为边坡的最优治理措施。岩质边坡支护效果评价流程见图1。

2 工程应用

2.1 工程概况

图1 岩质边坡支护效果评价流程

某料场位于某坝址下游，距坝址约7 km，沿河长约800 m，分布高程1690～2000 m，地形坡度40°～45°，开采坡比 1∶0.4 ～1∶0.3，部分强卸荷岩体采用1∶0.5，每隔30 m设置1条3 m宽马道，分10级开挖。料场地层岩性为前震旦系斑状流纹岩夹少量含绢云母片岩，岩石弱～微风化，岩质致密坚硬。基岩主要发育有4组构造裂隙，L1:N65°E/SE∠80°;L2:N25°～30°E/NW∠70°～75°;L3:EW/S∠80°～85°;L4:N45°～50°W/SW∠50°～60°。料场区域地下水不发育，无需考虑渗流影响。

2.2 边坡处理措施确定

根据地质资料中边坡的地质结构、断层分布情况和构造情况，将断面P10、P11、P12和P14作为控制断面［14］。采用 Morgenstern-Price法，对地震工况下终采边坡进行稳定计算。P10、P11、P12和P14安全系数分别为 0.973、0.985、0.952、0.933和0.991。

料场终采边坡为B类Ⅲ级边坡。根据DL/T 5353—2006《水电水利工程边坡设计规范》，采用边坡设计安全系数的下限值，即偶然状况(地震工况)为1.00。计算结果可知，各控制断面安全系数均不满足要求，该边坡需要支护处理。由于该料场边坡滑移块体大，采用削坡治理方案不经济，故最终采用锚索支护进行处理。

2.3 边坡失稳风险分析

2.3.1 计算模型及参数

基于FLAC3D软件，采用三维等参元对边坡地质模型进行网格划分，裂隙、次级小断层和挤压破碎带采用薄层实体单元模拟。边坡计算模型共划分为97698个单元和102718个节点。模型底部施加固端约束，侧面施加法向约束。边坡开挖前后网格划分见图2。岩体和结构面的屈服和破坏准则采用Druker-Prager准则。料场边坡岩体和结构面力学参数见表1。

图2 料场边坡网格划分

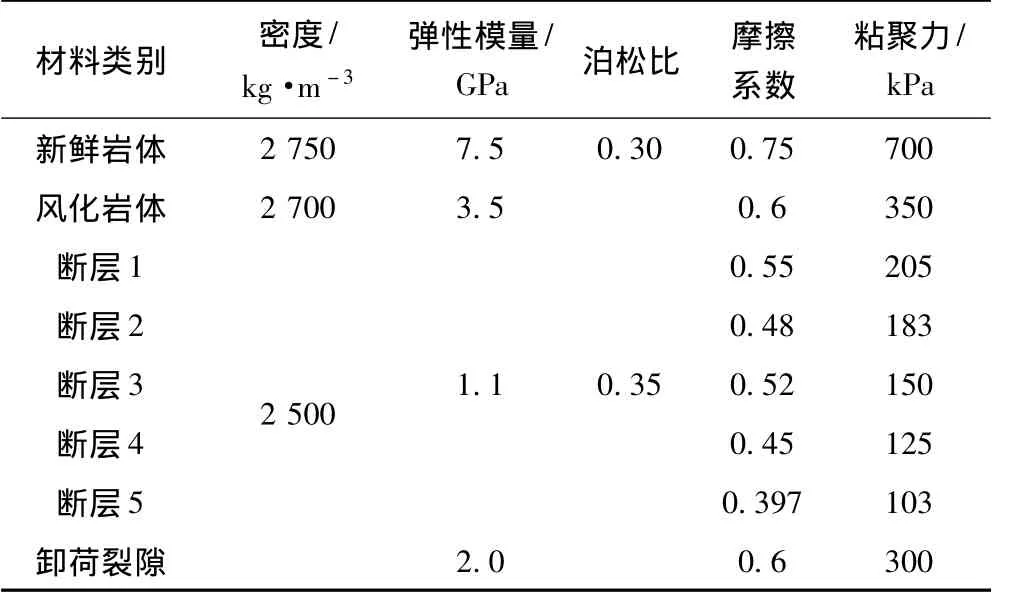
表1 料场边坡岩体和结构面力学参数

2.3.2 支护方案

锚索由锚索单元模拟，预应力锚索的锚固作用通过在锚索两端施加等效锚固力考虑，锚索支护按滞后开挖一级施加。采用开挖一级支护一级的方式，拟定了6种支护方案。方案1:无锚索支护;方案2:锚索数量5根，2、4、5、7、8级马道锚索1根;方案3:锚索数量10根，1～7、9马道布置1根锚索，8级马道2根锚索;方案4:锚索数量15根，1、3、6马道1根锚索，2、4、5、7马道2根锚索，8级马道3根锚索;方案5:锚索数量20根，1～4、7、9马道2根锚索，5、8马道3根锚索;方案6:锚索数量25根，1、9马达2根锚索，2～8马道3根锚索。以上支护方案锚索间隔均为6 m，吨位200 t。

2.3.3 不同支护量下的失稳风险

以岩体及结构面的摩擦系数和粘聚力为随机变量，考虑地震的超越概率，根据式(1)～(7)计算，得到不同支护量下边坡开挖失效概率。不同支护量下边坡失效概率见图3。从图3可知，同一开挖步下，随着锚索的增加，失效概率逐渐降低;相同锚索数量下，随着边坡不断开挖，失效概率逐渐增大。

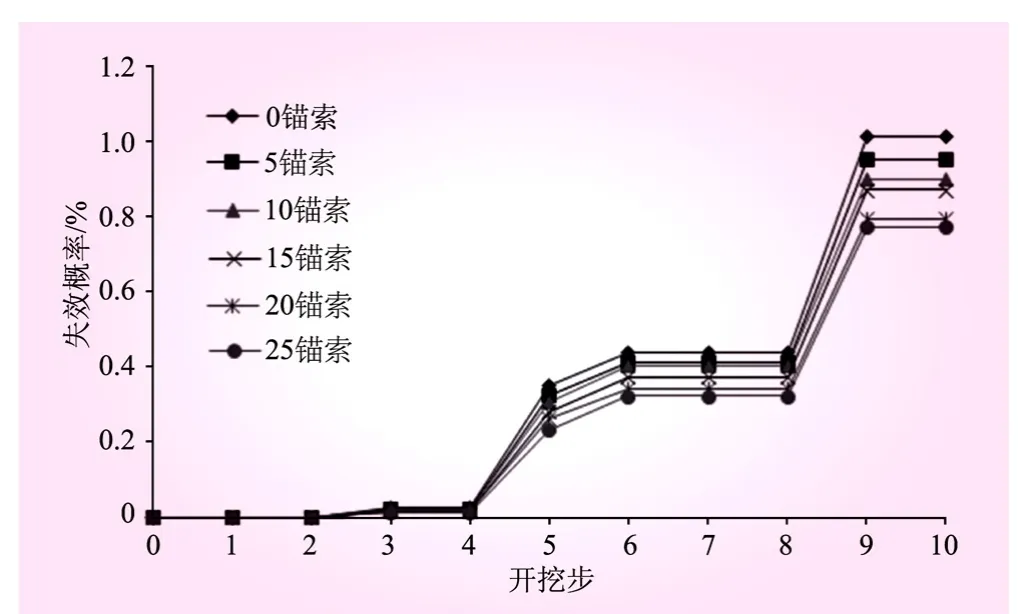
图3 不同支护量、不同开挖步下边坡失效概率

3 边坡支护效果评价

本文计算中，边坡滑移体滑移后的清除整理费为60元/m3，锚索造价为3.8元/m。根据本文给出的风险模型，得出不同支护量下各级开挖的风险损失(见图4)。从图4可知，在不同支护量下，边坡各级开挖的风险分布与边坡的失效概率分布类似。

图4 不同支护量下边坡开挖风险

在天然边坡和开挖1～4级中，边坡的失效块体的体积较大，其体积随边坡的开挖逐渐减小，边坡的风险值也呈现减小的趋势，但边坡的风险值很小接近于0，主要原因为天然边坡和开挖1～4级中边坡的失效概率很低。在第5级边坡开挖中，有缓倾角断层出露，与陡倾角断层形成不稳定的滑移块体，滑移块体的体积相对较小，其失效概率较大。第6级边坡开挖中，有缓倾角断层出露，并与陡倾角断层构成较危险的滑移通道，其失效块体的体积与失效概率均比第5级有所提高，风险值较大。第7、8级边坡开挖中，边坡没有新的断层出露，其风险主要受第6级开挖的滑移通道控制，两级开挖的风险值基本相同。第9级开挖中，新的缓倾角断层出现，与陡倾角断层构成新的较危险的滑移块体，其体积在整个边坡开挖过程中最小，但因其失效概率最大，故风险损失值也最大。完建边坡的风险，主要受第9级开挖后的滑移通道控制，其风险损失值比第9级开挖略有减小。

取完建边坡作为研究对象，将费用成本值作为经济指标衡量支护效益。完建边坡费用总成本与支护量曲线见图5。从图5可以看出，随着支护量的增加，边坡的失效概率减小，风险损失减小，开挖加固费用增加，两者之和总成本先减小后增加，在支护量为10处曲线出现最低点，表明支护方案3为较为合理的支护方案。

图5 不同支护量下完建边坡开挖总费用

4 结论

本文对某工程料场边坡在不同支护条件下进行可靠度计算，应用经济风险评价方法对不同支护方案进行评价，得到以下结论:

(1)结合可靠度计算成果，将计算得出的失效概率量化，以失效后造成的经济损失作为评价指标，得到边坡风险损失随支护量增加而降低，支护量越多，边坡的失效概率越小，即边坡越安全的结论。与计算得到的失效概率规律相同，证明了该方法的可行性。

(2)完建工况下边坡支护的总成本随支护量的增加先减少后增加，出现极小值拐点，说明采用200 t级锚索拟定的支护方案是可行的，找出了边坡失效风险与经济损失的平衡点，并最终确定了较为合理的支护方案。

［1］DUZGUN H S B，YACEMEN M S，KORPUZ C A.A methodology for reliability-based design of rock slopes［J］.Rock Mechanics and Rock Engineering，2003，36(2):95-120.

［2］LOW B K.Reliability analysis of rock slopes involving correlated nonnormals［J］.International Journal of Rock Mechanics and Mining Sciences，2007，44(6):922-935.

［3］LOW B K.Efficient probabilistic algorithm illustrated for a rock slope［J］.Rock Mechanics and Rock Engineering，2008，41(5):715 –734.

［4］JIMENEZ-RODRIGUEZ R，SITAR N，CHACON J.System reliability approach to rock slope stability［J］.International Journal of Rock Mechanics and Mining Sciences，2006，43(6):847-859.

［5］张兴，廖国华.多滑动面边坡的破坏概率［J］.岩土工程学报，1990，12(6):55-62.

［6］谭晓慧.多滑面边坡的可靠性分析［J］.岩石力学与工程学报，2001，20(6):822-825.

［7］吴震宇，陈建康，许唯临，等.岩质边坡稳定的体系可靠度分析及工程应用［J］.四川大学学报:工程科学版，2008，40(2):32-37.

［8］李典庆，周创兵，胡冉.基于n维等效方法的岩质边坡楔体稳定体系可靠度分析［J］.岩石力学与工程学报，2009，28(7):1415-1424.

［9］王伟，杨敏，刘德富.基于经济风险分析的边坡稳定性评价［J］.同济大学学报:自然科学版，2004，32(12):1603-1607.

［10］田斌，张萍，刘德富.岩石高边坡加固方案决策的经济风险分析［J］.工程地质学报，2007，15(Sl):502-506.

［11］曾晟，杨仕教，谭凯旋，等.基于可靠度的圆弧滑动边坡经济风险分析模型优化方法［J］.南华大学学报:自然科学版，2009，23(4):107-110.

［12］吴世伟.结构可靠度分析［M］.北京:人民交通出版社，1990.

［13］DITLEVSEN O.Narrow reliability bounds for structural system［J］.StrutMech，1979，4(1):117-122.

［14］李鹏，何江达，谢红强，等.地震作用下岩质边坡动力响应分析［J］.水力发电，2014，40(2):41-45.