镍矿运输船沉没机理的数值模拟分析

邹友家，沈 淳，奚祥英（上海海事大学 商船学院，上海 0035；武汉理工大学 管理学院，武汉430063）

镍矿运输船沉没机理的数值模拟分析

邹友家1，沈 淳1，奚祥英2
（1上海海事大学 商船学院，上海 200135；2武汉理工大学 管理学院，武汉430063）

近几年来，多条装运红土镍矿的船舶在南中国海倾覆沉没，引起业界的震惊。红土镍矿是一种非常特殊的矿物质，在运输过程中，如果船舶遭遇风浪，或船舶本身长时间的振动，都会导致该矿石的表面液化。液化后的混合液体具有较强粘性，可以形成自由液面。但由于现存的用于计算船舶自由液面的方法不适合于具有较大粘性的液体，因而无法解释运输该种货物船舶倾覆沉没的原因。所以，该文采用数学建模的方法，对运输红土镍矿的船舶进行了模拟计算。得出的结论是当流体的惯性力大于流体的粘性剪力时，粘性流体对船舶的作用力矩随时间的变化总趋势是逐渐增大。当流体产生的横向惯性力远大于流体的剪切阻力时，流体将会挣脱剪切阻力的束缚，迅速滑向船舶的一侧，使船舶的横稳性迅速消失，最终导致船舶很快倾覆沉没。

红土镍矿；粘性液体；液化；粘性剪力崩溃；倾覆沉没

0 引 言

随着我国经济的高速发展，国内对镍矿的需求急剧增加，不可避免地导致了镍矿运输船的迅速增加。但是，自从2010年以来，相继有多条载重吨在5万左右的镍矿运输船在南中国海附近翻沉，造成了重大的人员伤亡与财产损失，引起了国际航运界的高度关注。

研究表明，这些事故与船舶所承载的货物的特殊属性有关。含有高氧化铁的粘土类土质的镍矿（俗称红土镍矿）所含水分达到30%～40%，这种镍矿物质液化后形成的流体具有较大的粘性[1]。传统的船舶稳性理论认为，粘性流体对船舶的稳性具有正面影响，亦即当船舶向一舷发生倾斜时，粘性流体可以产生阻力，阻止船舶继续向该侧倾斜。因而，所有有关船舶稳性理论的教科书都只研究非粘性流体对船舶稳性产生的影响，即船舶的自由液面理论。但是，随着多条镍矿运输船的翻沉，出现了船舶的自由液面理论无法解释的现象。因此，有必要通过对船舶翻沉的过程建立数学模型，动态数值模拟镍矿运输船的沉没，从而可能找到粘性液货的粘性系数与船舶的横摇周期、振幅等变量之间的关系。通过对镍矿运输船舶的翻沉过程进行数值模拟，也许可以找到镍矿运输船沉没的真正原因。越来越多的研究表明，粘性流体可能并不总是对船舶的稳性具有正面影响。

1 数值模拟研究

通过对海难事故船舶的调查了解得知，这些船舶有些共同点：出事船舶都是满载红土镍矿，船上所有导航设备、主机副机及舵设备在当时都处于良好状态，出事海域当时都有6～8级的横风及2～3 m左右的横浪，但倾覆沉没的船舶状况有好有坏，总的说来，大部分船况较好，有的船甚至是刚下水不到一年的新船，这就基本上可以排除是由于船舶纵向强度不够造成船舶瞬间断裂的可能性。

根据船舶沉没之前的最后通讯记录及幸存者事后回忆，船舶在沉没之前都向一侧发生了倾斜，随即倾覆沉入海底。由此可以推断，船舶的稳性消失可能是造成船舶遇难的主要原因。那么，散装矿石船的重心通常都是非常低的，其稳性为什么会一下子消失呢？

1.1 自由液面理论

红土镍矿粉是一种被水分凝聚着的矿粉。当含水量超过35.7%时，遇到船舶摇摆和振动都会发生水份析出矿体表面的现象，称作矿粉的“液化流动”（Liquefaction）。初始产生矿粉液化现象的含水量，被称作流动水分点FMP（Flow Moisture Point）。液化析出的水分会聚集在红土镍矿的表面，形成自由液面，从而对船舶的初稳性高度GM值产生负面影响。国内有研究人员利用自由液面对稳性影响的计算公式对稳性损失进行了计算。货物表面自由液面对稳性影响的计算公式为：LB（3×）γ×2/12×D。式中：货舱长为L，宽为B，排水量为D，液体密度为γ。以一条排水量为21 000 t，5个货舱的散货船为例来进行稳性损失的计算，稳性变化值为：ΔGMi=-0.38 m。

研究人员假定船舶开航时GM为0．4 m，那么船舶在风浪中航行，红土镍矿粉游离出水份，导致稳性损失达0.38 m，可能会出现初稳性高度为负值，在外力的作用下可能会导致船舶向一侧倾斜，以致倾覆[2]。

但是，以上的分析方法值得商榷。一般说来，运输散装镍矿石的船舶，其货物堆装高度都在大舱深度的一半以下，保守地估算，初稳性高度值一般都会大于1 m，正常情况下是1.5-2.5 m，有的甚至更大[3]。因此，由于自由液面的存在而使船舶的初稳性高度损失0.38 m时，不太可能使船舶的稳性高度变为零或负值。那么，船舶倾覆沉没又该如何解释呢？

图1 红土镍矿在液化前与液化后的对比Fig.1 Lateritic nickel ore before and after liquefaction

1.2 数值模拟的建模

通过大量的调查研究，我们发现红土镍矿是一种非常特殊的货物。当其水份含量超过35.7%时（还需进一步测试数据的可靠性），如果船舶长时间振动或在风浪的作用下就会发生液化现象，货物的表面就会析出“一层水”。由于红土镍矿是一种有较强粘性的物质，析出的水份不会通过货物流到舱底，而是附着在货物的表面。而且，析出的水份不完全是水，而是一种水与腐泥土的红色混合流体，如图1。根据各矿区产出的矿石成分及化学组成不同，混合液体的粘度有很大的不同。

目前，计算自由液面对稳性的影响是有条件的，即液体的粘度可以忽略不计。当液体的粘度不能忽略的时候，现存的计算自由液面对稳性高度的影响的公式就不再适用。这也许可以解释为什么上述算法不能解释船舶稳性消失的原因。

当船舶装载粘性液货在风浪中航行时，粘性液货必然产生晃荡现象。大幅晃荡时，自由液面的运动具有强烈的非线性。图2所示为外力作用下三维货舱坐标系统。

二维不可压缩带自由表面的粘性流体运动，其控制方程分别由连续方程[4]

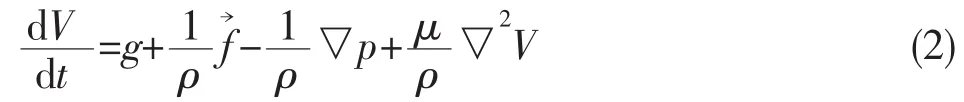
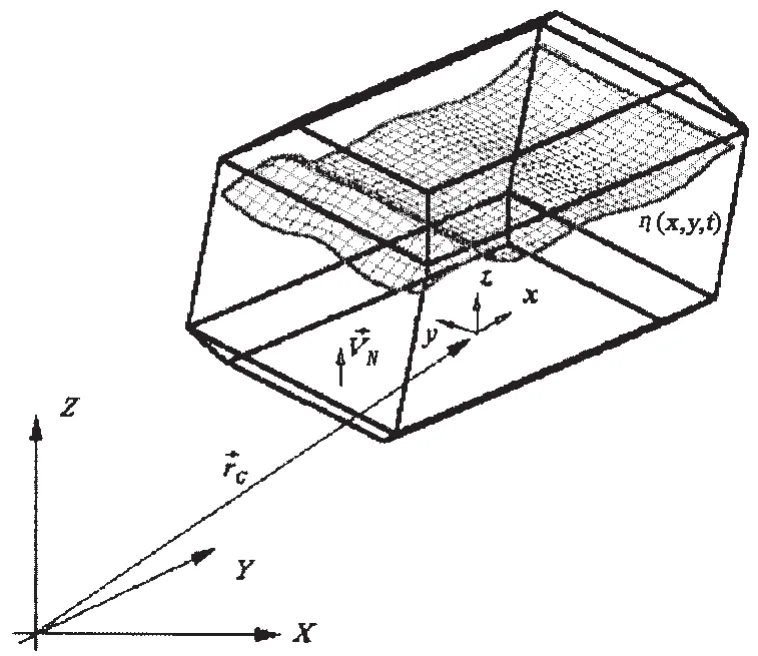
图2 外力作用下3维货舱坐标系统Fig.2 Coordinate systems for a three-dimensional tank under forced excitation

式中：a为质点o相对于固定坐标系的平均加速度，ω为船舶横摇的角速度，rG为从o点出发的矢径。

尽管当今有多种方法处理边界问题，但本文主要采用数值方法解决流体在舱内运动产生的晃荡。由于流体在舱内的晃荡表现为强烈的非线性，特别是接近共振区时。这些非线性包括破碎波、飞溅、喷射流以及冲击波等。若要将这些因素全部考虑进去是很困难的，而且，有些因素对本研究没有重大的意义。因而，流体的自由液面边界可以认为是一个单值函数。运动自由液面边界条件可以写成[5]：

式中：η为自由液面高度，u为速度矢量。

1.3 数值方法

由于有些局部的流体不具有普遍意义，因而我们可以使用一种快速有效的数值方法来模拟流体的运动[6]。国外学者Kim利用由Hirt提供的SOLA方法对不带斜面的三维容器（四角均为直角）成功进行了模拟。而我们则利用同样的方法来处理带有斜面（靠近舱底的一段侧面舱壁）的三维容器。具体的方法如下：

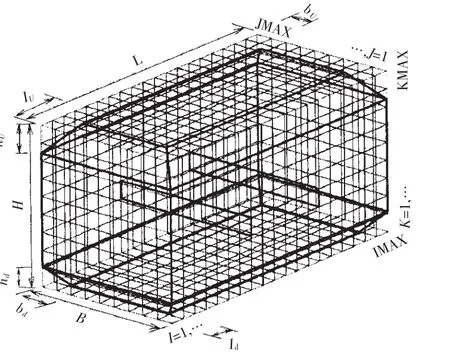
图3 棱型容器笛卡尔网格Fig.3 Cartesian grids for a prismatic tank with internal members

首先，将容器的体积离散为三维网格（I，J，K），采用笛卡尔交错网格，速度分量定义在网格的边界，而压力则在网格的中心，如图3。在SOLA方法中，瞬时压力和速度的计算采用迭代法。迭代法的第一步是计算伪速度[5]：

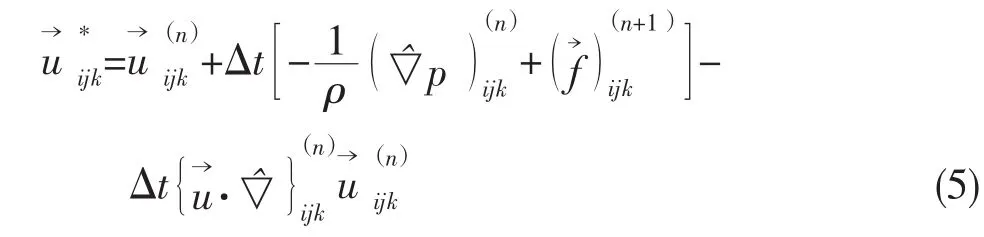
式中：Δt是时间分量，＾表示离散梯度，下标i，j，k表示在x，y，z方向的网格指数，上标n表示第n步。将（5）式代入连续性方程，我们就可以计算出压力改正值：

式中：Δ（x，y，）

z为在x，y，z方向的空间分量，因此，实际速度可以写成：

利用（6）式以及（7）式进行的压力与速度改正应该在每一个网格中都要做。改正的速度可以代入（6）式进行下一步的压力改正，这种迭代方法要一直运用下去，直到压力改正值在容许的误差范围内。

上式对有限差分中的对流项灵敏度较高。Hirt提出了将二阶中心差分法与一阶逆风差分法结合的方法[7]。采用分量参数α，则可以合成为：

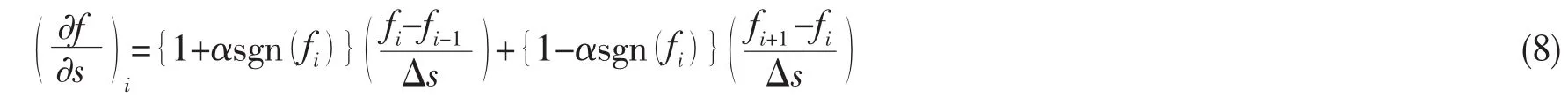
很明显，在一阶逆风差分中，如果参数α增大，例如增加到接近1时，将会造成数值衰减。方程（4）的离散形式可以写成：

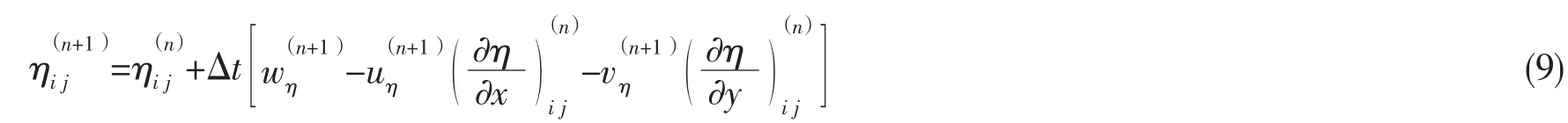
式中：wη，uη，vη为自由液面的速度分量，可以通过内插求得。液面坡度项可以用方程（8）的有限差分形式进行估算。特别要注意的是，为了克服锯齿波对方程稳定性造成的影响，需要使用数值滤波[9]。

由Longuet Higgins以及Cokelet提出的5点式公式对解决水波问题非常有用，对本研究也仍然适用[10]：

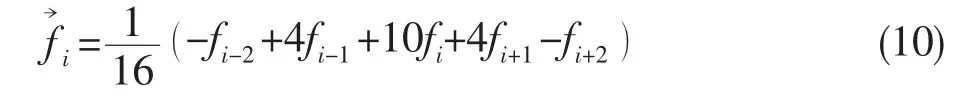
通过运用Miyata et al提出的3维不规则星方法[11]，可以满足方程（2）中自由液面交叉点各点的动态压力。该方法是基于6个相邻点的泰勒压力级数展开式，如图4。

在每一个自由液面网格，其中心压力可以写成：

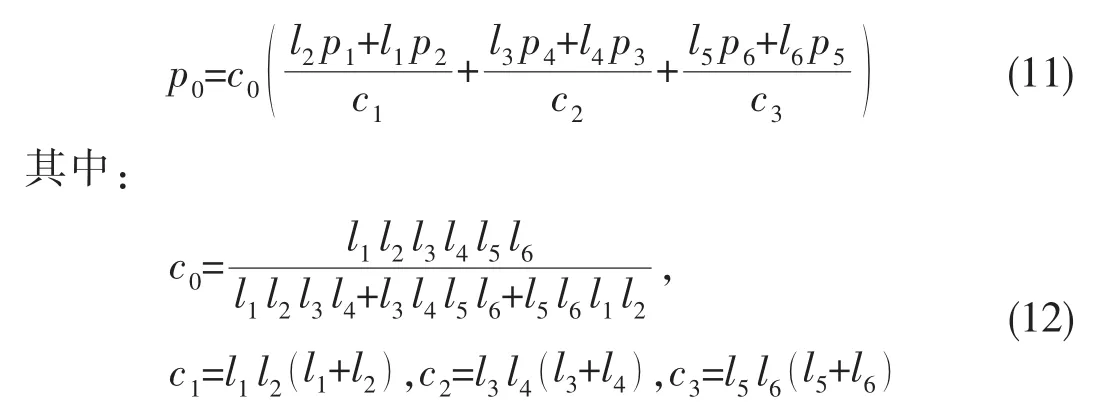
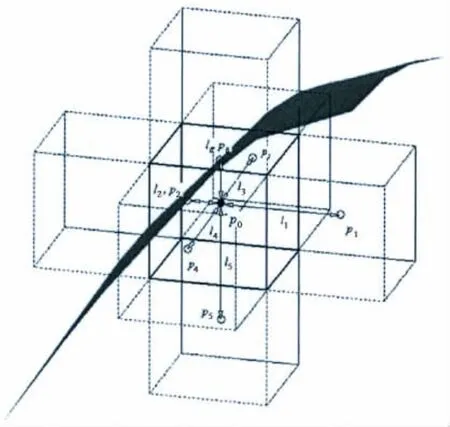
图4 3维不规则星方法的6点示意图Fig.4 Six points for the three-dimensional irregular-star method

式中：li是到第i个相邻点的距离。如果第i个相邻点位于自由液面上，则pi就应该等于大气压力。对于单值自由液面的剖面，可以认为5点中的最大值等于大气压力[10]。

1.4 模拟船舶横摇的影响

假定波浪对船舶产生一个周期性的扰动，其扰动力矩可以表示为[11-14]：

船舶运动的方程为：

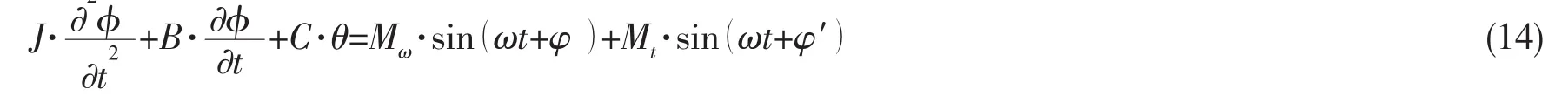
2

式中：J为船舶相对于纵轴的船舶惯性及附加质量惯性，φ是船舶的横摇角，B是阻尼系数，C是复原力矩，Mω是每一种波浪频率引起的扰动力矩，φ是扰动相位，Mt为流体的力矩振幅，φ′是相位滞后角。

2 数值模拟结果与分析

根据以上建立的数学模型，我们可以动态地模拟出粘性液体对舱壁的压强随时间的变化关系曲线图。现在以一条载重吨为5万吨的散货船为例（事故船的载重吨均在5万吨左右），满载红土镍矿，航速12 Kn，吃水11 m，风力6～8级，左舷受风，横浪，浪高2～3 m，横摇角6°，周期10 s。从图5可以看出，在流体粘度很小的情况下，舱壁所受压强呈现准周期变化。

船舶在外力的作用下，一定会产生一个外力矩，这个外力矩由风浪作用在船舶上的力矩与粘性流体作用在船舶上的力矩组成。由图6可以看出，风浪作用在船舶上的力矩呈现准周期性变化。

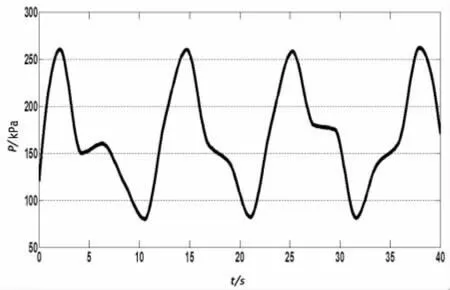
图5 舱壁所受压强与时间的关系Fig.5 Pressure on ship’s wall vs time

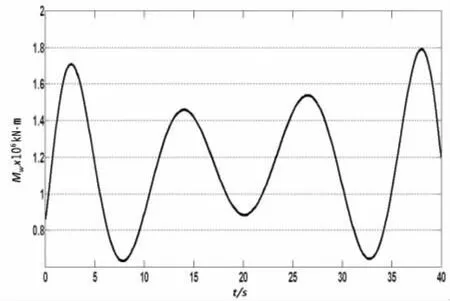
图6 风浪作用在船舶上的力矩与时间的关系Fig.6 Moments of winds and wave acting on ships vs period

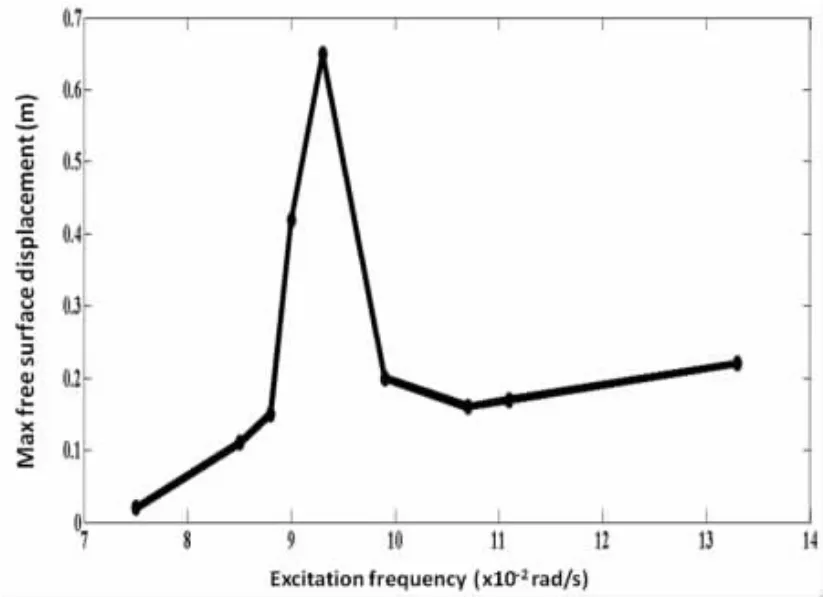
图7 自由液面位移与外激励频率的关系Fig.7 Free surface displacement versus excitation frequency

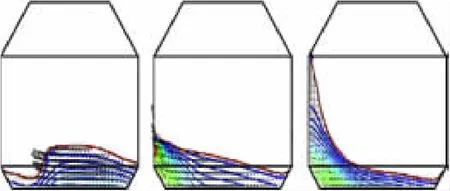
图8 速度矢量与压力场在3个时刻的模拟图：h/B=0.026，s/B=0.1，Te=10 sFig.8 Velocity vector and pressure contour at three time steps:h/B=0.026,s/B=0.1,Te=10 s

模拟实验表明，当激励频率与船舶的固有频率接近或相等时（f=0.093 1 rad/s），自由液面产生的位移（液面离开原来的水平位置）最大。外力（风浪）所做的功主要消耗在使船舶产生横摇运动以及使自由液面势能增加上（其它的消耗暂时忽略不计）[11]，见图7。

由于镍矿的比重大，完全液化后其堆装高度通常只占大舱高度的五分之一左右，因而做低液位模拟更符合实际情况。图8是对液位高度、速度场和压力场的数值模拟。h为液面高度，B为船宽，s为横荡位移，Te为激励周期。

但是，粘性流体（本例为镍矿混合液体）在外力的激励下，其力矩随着时间的变化与风浪对船舶的作用力矩随时间的变化有很大的不同。风浪对船舶的作用力矩随时间的变化具有准周期性。但粘性流体对船舶的作用力矩可以分为2个阶段：当惯性力小于粘性剪力时，粘性流体对船舶的作用力矩也呈准周期变化；当惯性力大于粘性剪力时，粘性流体对船舶的作用力矩随时间的变化总趋势是逐渐增大。增大的幅度与流体的粘度系数、船舶的横摇振幅及风浪周期有关。如图9.当船舶的横摇振幅增加时，流体产生的惯性力就会增加。而当流体产生的横向惯性力大于流体的剪切阻力时，流体将会挣脱剪切阻力的束缚，迅速滑向船舶的一侧。使得粘性流体作用在船舶上的力矩迅速增大，船舶的横稳性可能迅速消失，从而引起船舶的倾覆。

3 结 论

本文利用数学模型方法对载运粘性流体的船舶进行了稳性分析与计算。得出的结论是：当流体的惯性力大于流体的粘性剪力时，粘性流体对船舶的作用力矩随时间的变化总趋势是逐渐增大。当流体产生的横向惯性力远大于流体的剪切阻力时，流体将会挣脱剪切阻力的束缚，迅速滑向船舶的一侧，使船舶的横稳性迅速消失，最终导致船舶很快倾覆沉没。

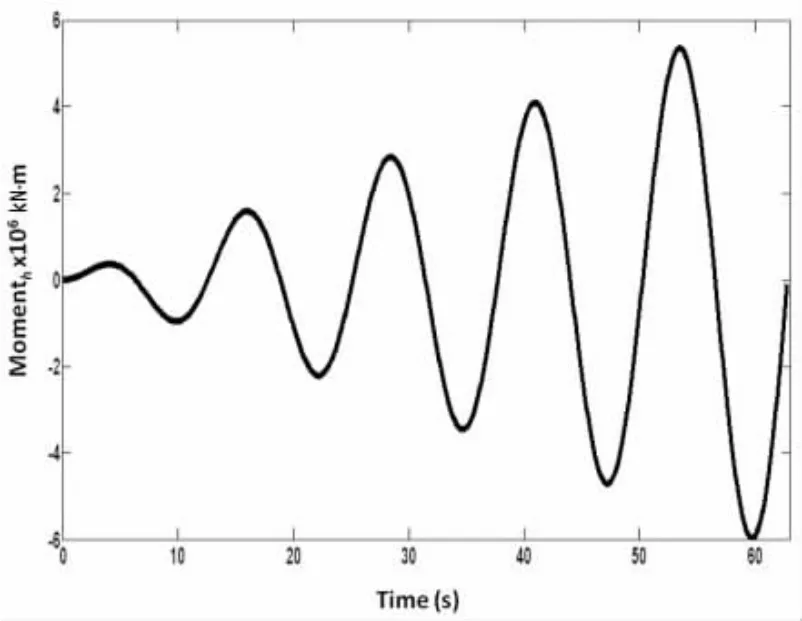
图9 粘性流体作用在船舶上的力矩与时间的关系（当惯性力大于粘性剪力时）Fig.9 Moments of viscous liquid acting on ships vs period(when inertial force is greater than shear stress)

上述结论还需要做进一步的研究，还需要进行更多的实验，以便确定较为准确的船舶横摇振幅，周期与流体粘性系数的关系。另外，风浪对船舶的作用具有非对称性，往往是从船舶的一侧作周期性的打击，而不是两侧交替打击，这样，我们的数学模型还需要进一步修改和完善，以便与实际观测的结果相一致。

[1]崔建辉,王建平.海运红土镍矿的安全运输[J].航海技术,2011,6:30-33. Cui Jianhui,Wang Jianping.Safe transport for lateritic nickel ores[J].Marine Technology,2011,6:30-33.

[2]雷 海.红土镍矿粉的安全运输[J].航海技术,2011,1:27-28. Lei Hai.Safe transport for lateritic nickel ore[J].Marine Technology,2011,1:27-28.

[3]李荣辉,徐邦祯.基于临界横倾角的散装谷物船舶稳性衡准[J].航海技术,2009,6:26-27. Li Ronghui,Xu Bangzhen.Stability norm for grain carriers based on critical heeling angle[J].Marine Technology,2009,6: 26-27.

[4]朱仁庆,方智勇,张照钢,等.Level-set法预报液舱内剧烈晃荡引起的冲击压强[J].船舶力学,2008,12(6):345-451. Zhu Renqing,Fang Zhiyong,Zhang Zhaogang,et al.Level-set method for predicting impact pressure induced by violent sloshing in a tank[J].Journal of Ship Mechanics,2008,12(3):345-451.

[5]Kima Yonghwan,Shin Yungsup,Lee Kwanghyun.Numerical study on slosh-induced impact pressures on three-dimensional prismatic tanks[J].Applied Ocean Research,2004,26:213-226.

[6]贺俊松,陈 震,肖 熙.五体船大倾角稳性研究[J].船舶工程,2007,29(5):12-15. He Junsong,Chen Zhen,Xiao Xi.Study on the stability at large angle of the pentamra[J].Ship Engineering,2007,29(5): 12-15.

[7]Hirt C W,Nicholas B D,Romero N C.SOLA-a numerical solution algorithm for transient fluid flows[R].Los Alamos Scientific Laboratory Report,1975,LA-5852.

[8]鲁 江,马 坤,黄武刚.斜浪长峰不规则波中船舶复原力变化计算[J].中国造船,2010,51(3):11-17. Lu Jiang,Huang Wugang.Calculations on the righting forces of ships in irregular waves with long inclined sea[J].China Shipbuilding,2010,51(3):11-17.

[9]丁仕风,唐文勇,张圣坤.速度突变情况下液化天然气船液舱内晃荡问题的仿真[J].上海交通大学学报,2008,42(6): 920-923. Ding Shifeng,Tang Wenyong,Zhang Shengkun.Simulation of liquid sloshing in the cabin caused by liquefied natural gas ship’S variable speed[J].Journal of Shanghai Jiaotong University,2008,42(6):920-923.

[10]Longuet-Higgins M S,Cokelet E D.The deformation of steep surface waves on water.I.A numerical method of computation[J].Proc R Soc,1976,A350:1-26.

[11]Miyata H,Inui T,Kajitani H.Free surface shockwaves around ships and their effects on ship resistance[J].J Soc Naval Architect Jpn,1980,147:1-9.

[12]雒高龙,任慧龙.超大型LNG船晃荡压力直接计算法[J].造船技术,2010,297(5):7-10. Luo Gaolong,Ren Huilong.Direct calculations of sloshing forces for the super LNG[J].Shipbuilding Technology,2010, 297(5):7-10.

[13]刘新立,严仁军,史 政,等.基于MSC.Dytran的液舱晃荡分析[J].船海工程,2010,39(2):44-47. Liu Xinli,Yan Renjun,Shi Zheng,et al.Sloshing analysis of liquid tanks based on MSC.Dytran[J].Ocean Engineering, 2010,39(2):44-47.

[14]陆志妹,范佘明.船舶液舱晃荡研究进展[J].上海造船,2010,2:14-30. Lu Zhimei,Fan Sheming.Outlooks of sloshing research[J].Shanghai Shipbuilding,2010,2:14-30.

Numerical simulations on the mechanisms of the capsizing of bulk nickel ore carrier

ZOU You-jia1,SHEN Chun1,XI Xiang-ying2
(1 Shanghai Maritime University,Shanghai 200135,China;2 Wuhan University of Technology,Wuhan 430063,China)

A number of bulk nickel ore carriers capsizing in South China Sea have made shipping industry shocked.Clay lateritic nickel ore is characterized by liquefaction on the surface under the influence of waves or long time vibrations during transportation.The blending liquid after liquefied is highly viscous and can generate free surface.However,the existing methods based on the calculation of GM values fail in explaining the capsizing of the carriers during transportation.In this paper,the mathematical modeling is adopted to make a thorough analysis to the mechanisms of capsizing.The results show that the imbalance of the shear force leads to the free movements of the liquid cargoes as the inertial force of the liquid cargoes is greater than that of the shear stress,and thus caused a loss of stability.Finally,the increasing external moments result in the capsizing.

clay lateritic nickel ore;viscous liquid;liquefaction;shear stress;collapse;capsizing

U661.32

A

10.3969/j.issn.1007-7294.2015.08.004

1007-7294（2015）08-0912-07

2015-01-28

邹友家（1964-），男，博士，高级船长，E-mail:marscar@126.com；

沈 淳（1966-），男，副教授；奚祥英（1966-），女，副教授。