基于粒子群优化的多智能体协作进化方法
马子鹏
(西安邮电大学自动化学院,陕西西安710121)
0 前言
传统的多智能体系统的控制方法主要是集中式和由上到下的分层式[1],但这些方法违背了智能体的自适应性和灵活性以及相对独立性的思想,并且有过度依赖主控制器的致命缺陷。因此,分散的自治的多智能体如何利用集体行为相互协作高效地共同完成单个智能体难以完成的复杂任务,是研究设计多智能体系统的核心问题之一。
群智能是人们对自然界的诸如蚂蚁、鸟群觅食等群体性活动进行研究总结规律,得出的智能组合优化算法。现在研究较多的群智能算法有蚁群算法、遗传算法、粒子群算法、免疫算法等。这些群体就像天然的多个智能体,自然而然地人们将群智能优化方法应用到多智能体的协作上。在多智能体系统中,可以在没有全局规划和命令的控制下通过个体间的局部感知、协作以及与环境的相互作用达到全局优化的目的[2]。多智能体系统中个体的简单局部交互来产生复杂的、适应的与目标驱动的群体行为,这个进化的系统能够在一个动态环境中根据改变而改善适应性[3]。本质上,涉及到的问题是环境的整体表示和搜索策略的优化。加拿大的Jiming LIU 在文献[3]用遗传算法实现了多智能体的集体行为。
粒子群优化算法 (Particle Swarm Optimization,PSO)由KENNDY 和EBERHART 等[4]于1995年提出,模拟生物活动和社会心理学行为的全局随机搜索算法,它的原理和机制简单,算法实现容易,具有鲁棒性、分布并行性和全局寻优的能力,是函数最优化方面的高效方法之一。本文作者尝试将该算法应用到无限传感网络多智能体的协作中,给出了用该算法实现多智能体协作的方法和Matlab 仿真的结果。
1 粒子群算法实现多智能体协作
1.1 多智能体系统
多智能体系统通常是由多个自治的、分布式的、异构的智能体所构成的复杂系统。各智能体之间互相通信,彼此协调,并行地求解单个智能体难以解决的复杂问题[5],因此能有效地提高问题求解的能力。一个具有协作进化机制的多智能体结构如图1 所示。
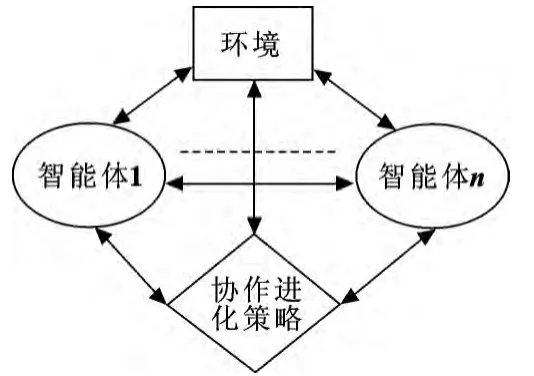
图1 带有进化机制的多智能体系统结构
带有协作进化机制的多智能体系统是一个靠集体行为来完成一个复杂任务的系统,集体行为在执行任务的过程中逐步进化,直至完成任务。在求解问题的过程中,智能体和环境之间通过局部感知连续获得经验,是一个在协作策略的作用下边进化学习边执行求解的过程,单个智能体能够从外界获取环境信息,可以独立自主地思考、行动来影响环境,智能体之间可以相互通信,实现分工协作。
1.2 粒子群算法实现多智能体协作进化
粒子群优化算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法,用于解决优化问题。优化问题的每个解都是搜索空间中的一个粒子,多个粒子构成粒子群。在搜索过程中,每个粒子要维护速度和位置两个向量,位置向量决定被优化的函数的适应值,这个函数被称为适应度函数,每个粒子还有一个速度决定它们飞翔的方向和距离。另外,每个粒子要维护自己的局部历史最优位置,算法要维护整个全局的历史最优位置,然后粒子们就追随着这两个最优粒子在解空间中搜索。由此可见,对于用粒子群算法实现多智能体协作进化的关键涉及到粒子的位置、速度向量和适应度函数在多智能体系统中如何表示和进化。
(1)多智能体粒子的表示方法
在算法中粒子进化时涉及到位置向量和速度向量,位置向量体现了粒子所代表的解在解空间的位置,适应度函数用该向量来评估粒子的优劣,是评估解质量的基础。速度向量表示解向量进化的方向和速率,是单步位置的变化。在基本的函数优化的粒子群算法中,位置是用一个函数的解向量表示,速度是和位置维数相同的向量。对于多智能体协作的粒子来说,一个问题的解由协作智能体的解共同组合而成,那粒子的位置也是由各个智能体的位置组合而成。假设有n 个智能体协作,每个智能体的位置的维数为m,则粒子的位置维数为m×n,结构如图2 所示。
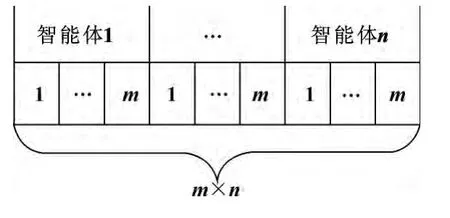
图2 多智能体粒子位置表示
(2)适应度函数的设计
要求该函数能够对粒子位置的优劣作出区分,对粒子的进化应该有好的导向性,从而提高粒子群的进化能力。要结合具体问题优化目标设计适应度函数,一般应满足较优的粒子位置适应度函数的值较大。为了使函数有更好的区分性能可以对适应性函数作一些修订,比如说线形变换、指数变换和乘幂变换等[6]。
(3)粒子群算法流程
当设计好粒子位置和适应度函数后就可以进行粒子群算法的操作,流程如下:
步骤1 初始化每个粒子,包括它们的速度和位置,设置个体最优位置pBest为当前位置,全局最优gBest为群体中最优的个体最优者。
步骤2 计算本代进化中每个粒子位置的适应度函数值。
步骤3 检查粒子当前的适应度函数值,如果比其个体最优值pBest大,则用该值更新pBest,如果该粒子的pBest比全局最优gBest的值大,则用pBest更新gBest。
步骤4 对每个粒子的速度v 和位置x 按下式进行更新:
式中:0 <ω <1 是惯量权重,c1和c2是加速系数,一般取2.0,rand1和rand2是随机产生的[0,1]之间的数值。
步骤5 如果没有达到结束条件,跳转到步骤2继续循环,否则结束。
2 实例仿真
实例用Matlab 对5 个智能体协作进行路径规划,把箱子推到目的地进行仿真。智能体推箱子采用文献[3]提到的人工排斥力模型。智能体分布在箱子的附近产生排斥力使箱子移动,该模型类似胡克定律,在距箱子一定邻域内距离越近产生的推力越大。箱子的移动由多个智能体的排斥力的合力决定,即多个智能体协作完成箱子的移动。该实例的适应度函数由三部分组成,一是全局信息,表示多个智能体合力的大小;二是表示合力的方向和目标方向的夹角,指出了箱子的运动方向多大程度上和目标方向一致;三部分表示的是个体智能体的局部作用,即智能体相对箱子的空间距离和的倒数,指出了智能体和箱子接近的程度;具体定义如下:

其中

式中:α、β、γ 表示每部分的权重,sum(fi)表示多个智能体和合力,θ 表示运动方向和目标方向的夹角,Di表示第i 个智能体和箱子的距离。
箱子的初始位置和目的位置在1 200 ×1 200 二维的范围内进行设置。粒子群算法的粒子个数为50,每个粒子的位置由5 个智能体相对于箱子坐标的空间位置向量构成,是一个10 维的向量,初始值由随机函数产生。图3 和图4 是分别采用遗传算法和粒子群算法实现多智能体协作推箱子的运动轨迹图。可以看到遗传算法在进化的开始阶段的轨迹是振荡的、无序的,随后曲线变得光滑最终到达目的地。相比较而言,粒子群算法在开始阶段振荡较小,这是由于粒子群算法收敛速度快的原因,并且粒子群算法箱子运行的轨迹偏离目标的程度也比遗传算法小得多。到达目标执行的迭代次数遗传算法k =51,粒子群算法是k=42。可见在本实例中,基于粒子群算法得多智能体协作比遗传算法收敛速度快,并且运动的方向与目标方向基本一致。另外,为了考察智能体对新目标的适应性,又进行了目标重置的实验,即当箱子移动到一个目的地后,重新设置一个目的地,让智能体把箱子再推到新目的地。图5 给出了重置目标的箱子运动的轨迹,从图4 可以看出,智能体通过42 次迭代到达第一次目的地,然后重置目的地后,迭代32 次到达了新目的地。这说明,基于粒子群算法的多智能体协作进化能够适应新任务的动态变化。
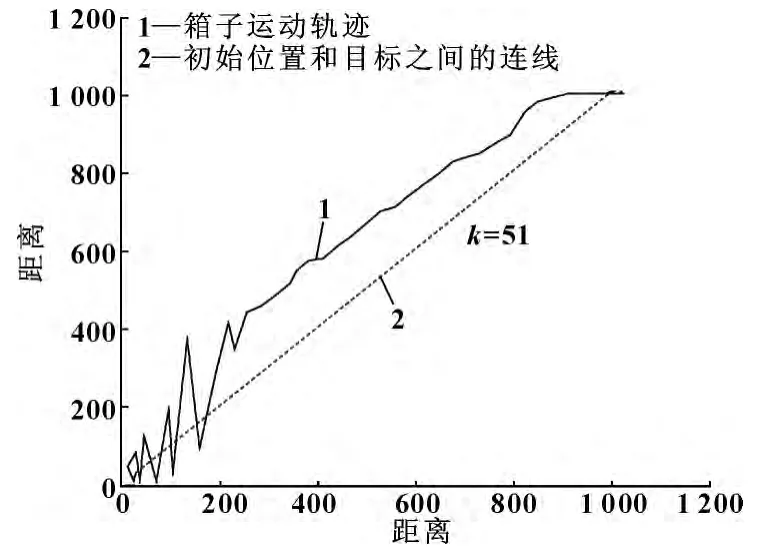
图3 遗传算法箱子的轨迹图

图4 粒子群优化箱子的移动轨迹图
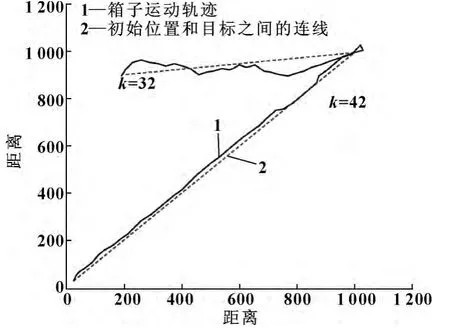
图5 重置目标的箱子运动轨迹
3 结束语
通过研究多智能体协作进化的机制和粒子群算法,提出了基于粒子群算法的多智能体协作进化方法。通过仿真实验,并通过和遗传算法进化比较,结果显示该算法能够有效减少前期搜索的振荡,加快收敛速度,验证了该算法的有效性。并且粒子群算法具有参数少、操作步骤简单的特点,是实现多智能体协作进化行之有效的方法。
[1]王越超,谈大龙.协作机器人学的研究现状与发展[J].机器人,1998,20(1):69-75.
[2]秦海力,耿丽娜,郑志强.群智能算法应用于MAS 系统协作的探讨[J].计算机仿真,2008,25(7):141-144.
[3]LIU Jiming.多智能体模型与实验[M].北京:清华大学出版社,2003.
[4]EBERHART R C,KENNEDY J.A New Optimizer Using Particle Swarm Theory[C].Proc.the Sixth Int.Symp.Micro Machine and Human Science,1995:39-43.
[5]GABER Heba,AMIN Safaa,SALEM Abdel-Badeeh M.A Combined Coordination Technique for Multi-Agent Path Planning[C].10th International Conference on Intelligent Systems Design and Applications,2010:563-568.
[6]张军.计算智能[M].北京:清华大学出版社,2009.
[7]ZHONG Weicai,LIU Jing,XUE Mingzhi,et al.A Multiagent Genetic Algorithm for Global Numerical Optimization[J].IEEE Trans on Systems,Man and Cybernetics,2004,34(2):1128-1141.
[8]BERNDT Jan Ole,HERZOG Otthein.Efficient Multiagent Coordination in Dynamic Environments[C].IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology,2011:188-195.
[9]ZHANG Haopeng,HUI Qing.Multiagent Coordination Optimization:A Control-Theoretic Perspective of Swarm Intelligence Algorithms[C].IEEE Congress on Evolutionary Computation,2013:3339-3346.
[10]王云,王俊,韩伟.基于进化算法的多智能体合作学习[J].山东大学学报,2010,40(6):8-11.
[11]韩伟,韩忠愿.基于黑板模型的的多智能体合作学习[J].计算机工程,2007,33(22):42-44.
[12]LI Xun,MA Hongxu.Particle Swarm Optimization Based Multi-Robot Task Allocation Using Wireless Sensor Network[C].Proceedings of the 2008 IEEE International Conference on Information and Automation,2008:1300-1303.

