3-RPC型并联机器人模糊滑模轨迹跟踪控制研究
刘运鸿,安梓铭,李雅琼,朱大昌
(江西玖发新能源汽车有限公司,江西赣州341000)
0 前言
并联机器人在很多领域都有广泛的应用,也发挥重要作用,如在武器系统、医学上等,但并联机器人机构系统复杂,有非线性、强耦合的特点,导致要对其进行控制就更困难,而且控制精度也不高,这给生产应用带来了很多不便[1-2]。人们对并联机器人控制的研究时间并不长,不透彻。为让其在工业化发展中发挥重要作用,必须加强对并联机器人的控制策略的研究[3-4]。滑模变结构控制在并联机器人中比较广泛,在并联机器人中很难有精确的数学模型,而滑模变结构可以不需要精确的数学模型,只要参数的变化幅值,加上滑模变结构控制对外界的干扰不那么敏感,并且滑模变结构控制不必要做专门解耦来解决内部耦合,其本身的设计过程就可以解耦。这样通过滑模变结构控制就可以很好地对并联机器人实现控制[5-6]。变结构与其他控制方式相结合控制效果会更佳[7-8]。
滑模变结构控制与传统的控制系统相比,控制简单,对数学模型的精确性要求不高,对外部干扰和参数变化有好的鲁棒性和完全的自适应性,并有降阶、解耦、动态性能好等优点[9-10]。机器人是典型的非线性系统,存在各种不可预见的外部干扰,滑模变结构控制能比较有效地应用于机器人控制中[11-12]。
本文作者设计了模糊自适应滑模变结构控制器,在Matlab 仿真软件进行仿真,得出仿真结果,通过结果分析可以证明模糊滑模变结构的控制精度更高,能更有效削弱抖振现象。
1 并联机器人轨迹规划
1.1 并联机器人运动学反解
3-RPC 并联机器人机构如图1 所示,其上(动)平台、下 (定)平台都为三角形,动,定平台由3 个支链连接构成,3 条支链的结构相同,即都为RPC 支链。每条支链中圆柱副轴线平行于定平台的一条边,转动副轴线平行于圆柱副轴线,且移动副轴线垂直相交于圆柱副和转动副轴线。3 条支链绕Z 轴呈120°对称分布。

图1 3-RPC 并联机构
如图1 可知,定平台各点的坐标为:

动平台各点坐标为:

由螺旋理论可得3-RPC 并联机构只做三维平动,所以该机构的欧拉角都为零,即α=β=λ=0;可知,R 的旋转矩阵为:
由机构的几何矢量关系,每组平行杆的矢量式可以表示为由并联机构的几何矢量关系,如图2 所示,每组平行杆的矢量式li可以表示为:
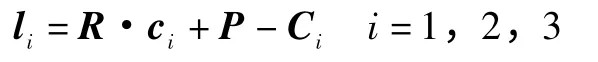
其中:ci是动平台上中点在动坐标系中的矢量,Ci在静坐标系中的矢量,P 为动平台原点在静坐标系中的矢量,R 为动平台姿态的方向余弦矩阵。由上式可得:


图2 机构的几何矢量关系
1.2 轨迹规划
机器人要完成规定的动作,则要对其进行相应的轨迹规划。而并联机器人结构相对复杂,工作空间表达相对困难,并有不确定性,所以对轨迹规划增加了很大的难度。因此,利用并联机器人运动学反解相对简单的特点,对其进行轨迹规划相对简单。所以采用运动反解做驱动位移轨迹跟踪。
2 滑模控制律的设计
设机器人的动态方程为

其中:q∈Rn为转动角度向量,M(q)为n ×n 维正定惯性矩阵,Vm(q)为n ×n 维向心哥氏力矩,G(q)为n×1 维惯性矩阵,τ∈Rn为各个支链的转矩向量,即控制输入。
机器人动力学系统具有如下动力学特性:
(1)惯性矩阵M(q)是对称正定阵且有界;
(2)M(q)-2C(q,q·)是一个斜对称矩阵,即对任意向量x,有:

(3)重力项满足G(q)≤gb,gb为q 的函数。
2.1 传统滑模控制设计
定义跟踪误差为:

定义误差函数为:

其中:λ=diag [λ1,…,λi,…,λn],λi>0。
定义

设计控制律为:

将式(6)代入式(1)得:

假设

2.2 模糊自适应控制律设计
采用模糊系统可以实现对任意连续函数的精确逼近。因此,可以用模糊系统自适应逼近控制的增益对其进行控制研究。运用乘积推理机,单值模糊器和中心平均解模糊器来设计模糊系统,用于表示模糊集的隶属函数设计为:

模糊系统的输出为:

其中

M 为模糊规则数量。
对模糊增益调整的控制律设计为

其中K= [k1,…,ki,…,kn],ki为第i 个模糊系统的输出。
将式(11)代入到式(1)得:


自适应律取为:

3 3-RPC 并联机器人数学模型
3-RPC 并联机器人三支路通道具有相似性,选择一条支路作为研究对象。单条支路的数学模型:

式中:J =L(Ja+Jm+i2J0),B =R(Ja+Jm+i2J0)+L(Bm+i2B0),W = R(Bm+ i2B0)+ KcKb。Kc是电动机转矩常数,J0是可以通过试验或机构分析确定的标称负载转动惯量;B0是可以通过试验或机构分析确定的标称负载阻力系数;Ja是转子的转动惯量;Jm是减速装置驱动边的转动惯量;i 是减速装置的速比;Bm是驱动侧的阻力系数;Kb是电机的反电势常数;L 是电枢的电感;R 是电枢的电阻。
4 系统仿真模型及结果
直流伺服电机以及伺服驱动器参相关参数:额定转矩为0.25 N·m,空载转速4 300 r/min,Kc=0.074 N·M/A,R =1.11 Ω,L =1.1 mH,Ja=3.11×10-5kg·m2,ⅠN=2.95 A,Kb=0.1 V (rad/s),Jm=0.002 7 kg·m2,Bm=0.003 7,i =40。将这些参数代入式(15)得

根据3-RPC 机器人运动要求,设计出模糊自适应增益滑模控制,如图3 中有3 个S-Function 函数,第一个S-Function 函数是该系统运动的期望轨迹,其函数为3-RPC 型并联机器人机构的运动学反解函数。第二个S-Function 函数为所设计的控制器,即模糊自适应增益滑模变结构控制器。第三个S-Function 函数为控制支路的数学模型。文中采用ode45,取系统仿真步长0.001 s。应用计算机通过对并联机器人模糊自适应增益滑模变结构控制仿真,可到得传统滑模变结构控制轨迹跟踪图,如图4,5 所示。

图3 系统仿真模型

图4 传统滑模控制的的轨迹跟踪

图5 模糊自适应增益滑模控制的轨迹跟踪
从图4 分析可知道,传统变结构控制在轨迹跟踪中有较高精度的轨迹跟踪。系统响应速度也比较快,在刚开始运行时控制系统就能立刻跟踪反应,控制运行相对平稳,当运行大约0. 6s时就能达到理想的跟踪效果。从图5 分析可知道,模糊自适应增益滑模控制轨迹跟踪中有更高精度的轨迹跟踪,系统响应速度也很快,在刚开始运行时控制系统就能立刻跟踪反应,控制运行相对平稳,当运行大约0.4 s 时能与期望轨迹相重合,说明达到了理想的跟踪效果。由上述仿真结果表明模糊自适应增益滑模控制要优于传统变结构控制,同时响应速度也更快,响应时间也更短。且都能达到对3-RPC 并联机器人的轨迹跟踪控制要求。
5 结束语
应用计算机Matlab 软件建模,对3-RPC 型并联机器人进行控制仿真分析。其仿真结果表明:传统滑模控制的跟踪精度不高,响应时间相对长,并在控制过程中出现抖振现象;通过比对分析可得出增益模糊控制可以明显消弱控制系统的抖振现象,响应时间明显更快。
[1]常兴,刘安心,房立丰,等.一种三维移动并联机器人机构及其运动学分析[J].机械传动,2012,36(6):25-28.
[2]莫贤.基于螺旋理论的3_PRS 并联机构的运动学建模及仿真[D].扬州:扬州大学.2009.
[3]刘奇帅,杨熙,杜翠国,等.利用遗传算法优化的神经网络求解并联机构位置正解[J].煤矿机械,2013,34(2):11-12.
[4]宗朝.不确定二自由度冗余并联机器人控制方法研究[D].南京:南京理工大学,2013.
[5]刘延斌,韩秀英,赵新华.3-RRRT 并联机器人解耦控制[J].哈尔滨工业大学学报,2009,41(12):247-249.
[6]朱彩红.2-DOF 并联机器人控制研究[D].镇江:江苏大学,2007.
[7]KIM S M,HAN W Y,KINM SJ.Design if a New Adaptive Sliding Mode Observer for Sensorless Induction Motor Drive[J].Electric Power Systems Research,2004,70:16-22.
[8]高国琴,丁琴琴,王威.RBF 神经网络滑模变结构控制在并联机器人中的应用[J].工业仪表与自动化装置,2012,42(2):35-39.
[9]丛爽,王杨,尚伟伟.自适应控制策略在并联机构上的应用[J].制造业自动化,2007,29(7):45-49.
[10]MUNOZ D,SBARBARO D.An Adaptive Sliding-mode Controller for Discrete Nonlinear Systems[J].IEEE Transactions on Industrial Electronics,2000,47(3):574-581.
[11]董超君,高国琴,宁珍珍.并联机器人的智能模糊滑模控制算法[J].机械设计与制造,2008,7(7):150-152.
[12]刘金琨.机器人控制系统的设计与MATLAB 仿真[M].北京:清华大学出版社,2008.

