等待时间受限的HFSP及其拉格朗日松弛算法

丁小丽，朱 军，刘 昶

DING Xiao-li1,2, ZHU Jun1, LIU Chang1

（1.中国科学院沈阳自动化研究所，沈阳 110016；2.中国科学院大学，北京 100049）

0 引言

混合流水车间调度问题（Hybrid Flow-shop Scheduling Problem, HFSP）是由Salvador于1973年首先提出来的。HFSP是一类复杂的组合优化问题，它是标准的flow-shop调度和并行机调度问题的综合，相当普遍地存在于化工、钢铁、制药等流程工业中[1]。

等待时间受限的混合流水车间调度问题广泛存在于钢铁生产，玻璃加工和塑料等行业，它的形成是由于生产过程中的高温连续性，要求工件在相邻两个阶段之间保持一定的温度，例如在钢铁生产过程中的炼钢-连铸-热轧过程中，连铸机对温度有严格的要求，为避免温度降低影响钢水质量，不允许钢水在工序间有过长的等待时间。因此，可将两阶段之间的温度要求转换为对等待时间的要求，从而形成了等待时间受限的混合流水车间调度问题。

目前，关于等待时间受限的HFS调度问题的研究较少。文献[2]研究了具有零缓冲能力和有限等待时间的多处理器HFS问题，以总加权拖期最小为目标，基于离散时间和混合整数线性规划提出了一种精确求解算法。文献[3]研究了以最小化makspan为目标的等待时间受限的HFSP，提出了一种启发式-禁忌算法来求解。文献[4]针对考虑交货期和等待时间受限的HFS调度问题，提出了一种结合回溯和邻域搜索的混合算法来进行求解。文献[5]研究了以最小化生产等待时间为目标的带工件和工位等待时间的混合流水车间调度问题，提出运用差分进化算法来进行求解。文献[6]研究了以最小化各工件的提前/拖期惩罚和为目标的带交货期和释放期的等待时间受限的HFS调度问题，采用约束满足优化算法和指派规则的混合算法来进行求解。

Gupta J N D[7]已经证明即使只有两个阶段且其中只有一个阶段包含多台并行机的HFSP是NP难问题，因此，本文要研究的更为复杂的HFSP也是典型的NP难问题。拉格朗日松弛算法[8,9]是解决生产调度问题的有效方法之一，可用于NP难问题的求解，它通过将复杂约束引入到目标函数，可将原问题分解为多个简单的容易求解的子问题，大大降低了问题的求解难度，可以获得问题的近优解。目前对于等待时间受限的混合流水车间调度问题的求解在算法方面集中于精确求解算法或者智能优化类的近似算法。因此本文创新性的将拉格朗日松弛算法用于等待时间受限的混合流水车间调度问题研究中，拓展了拉格朗日松弛算法的应用范围和混合流水车间[10,11]调度理论。

本文针对等待时间受限的混合流水车间调度问题，首先建立了以最小化加权完成时间为目标的HFSP模型，然后在此基础上设计相关的拉格朗日松弛算法来进行求解，最后通过实验数据验证算法的可行性和有效性。

1 HFSP问题描述及建模

所研究的等待时间受限的HFSP可描述如下： n个工件在流水线上经过相同的s个阶段的加工，每个阶段上有Mj台同构并行机，每个工件可以在阶段j的任意一台机器上进行加工，已知工件i在阶段j的加工时间为pij，同时工件i在相邻阶段j和j+1之间的等待时间不超过一定的时间上限aj。其中，每台机器一次最多加工一个工件，每一个工件在任意时刻最多只能在一台机器上进行加工，且加工过程是连续的，不允许发生中断。调度问题就是确定各个工件在各阶段的加工完成时间Cij，从而使得总加权完成时间达到最小。

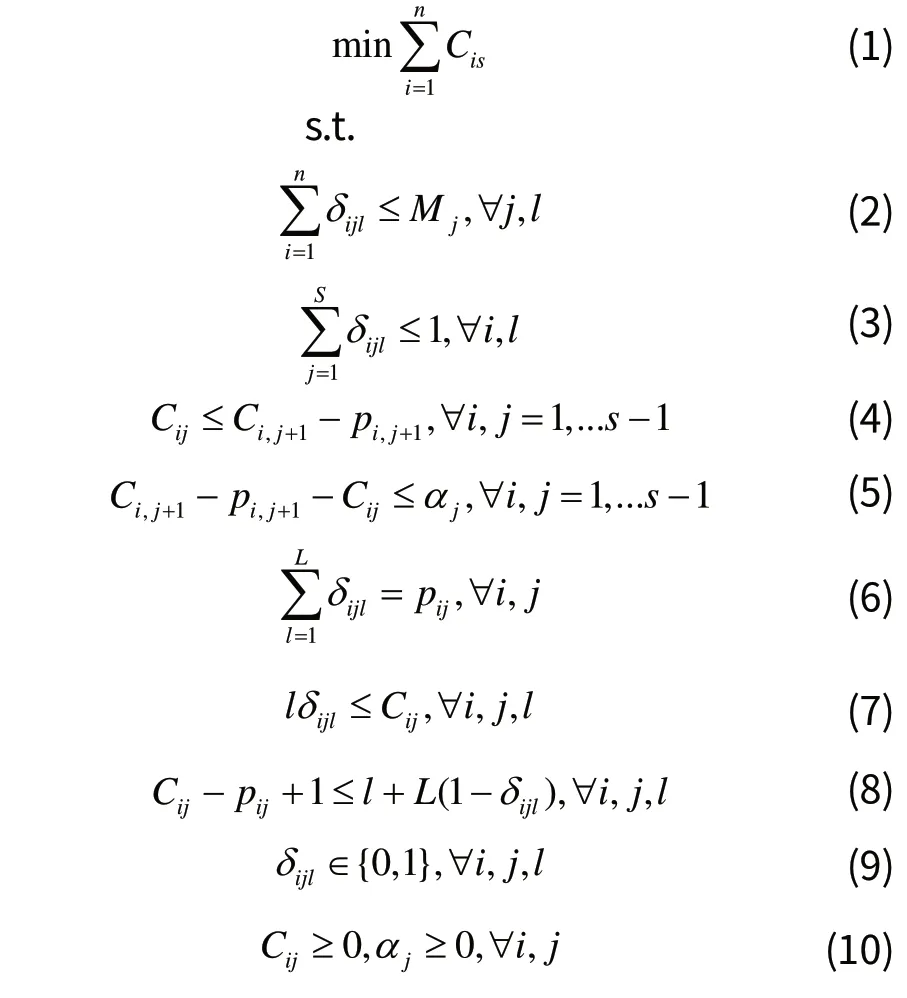
上述模型中目标函数(1)为所有工件的总加权完成时间。约束(2)表示机器容量约束，即同一时刻在同一阶段进行加工的工件数不超过该阶段的机器数；约束(3)表示同一工件在同一时刻最多只能在加工过程中的一个阶段进行加工；约束(4)为工件的时间优先级约束，表示工件只有在完成上一阶段的加工之后才能进入下一阶段的加工；约束(5)表示工件在相邻阶段之间的等待时间不超过一定的上限；约束(6)～(8)表示机器占用约束；约束(9)和约束(10)为相关变量的取值范围定义。

等待时间受限的HFSP调度问题模型就是在满足约束(2)～(10)的条件下将工件安排到各阶段的机器上进行加工，使得所有工件的总加权完成时间达到最小。

2 算法设计

拉格朗日松弛（LR）算法是解决生产调度问题的有效方法之一，可用于NP难问题的求解，它通过将复杂约束引入到目标函数，可将原问题分解为多个简单的容易求解的子问题，大大降低了问题的求解难度，可以获得问题的近优解。整个求解过程如下：首先通过引入一组拉格朗日乘子将复杂约束松弛到目标函数中，形成拉格朗日松弛问题；然后将得到的LR问题分解为一系列简单的子问题进行求解，最后对于松弛问题的解一般需要通过可行化来构造原问题的可行解；重复上述过程直至达到停止准则。可行解的目标函数值提供了一个最优解的上界，而对偶目标函数值为最优解的一个下界，这样拉格朗日松弛算法同时也为衡量解的质量提供了一个标准，解的质量可以通过两者之间的对偶间隙来进行衡量（对偶间隙=[可行解的目标值-对偶目标值]/对偶目标值）。

从上节所建立的模型中可以看出，约束(3)～(5)都耦合了不同的阶段，如果要基于阶段进行分解需要将这三个约束都进行松弛，松弛的约束越多，所得到的对偶目标值就越松，而只有约束(2)耦合了不同的工件，因此，本文所设计的拉格朗日松弛算法采用基于工件进行分解的策略，下面将详细的介绍拉格朗日松弛过程、子问题的求解、乘子的更新以及可行解的构造过程。

2.1 拉格朗日松弛

引入拉格朗日乘子向量 将约束(2)松弛到目标函数(1)中，形成下面的拉格朗日松弛问题：

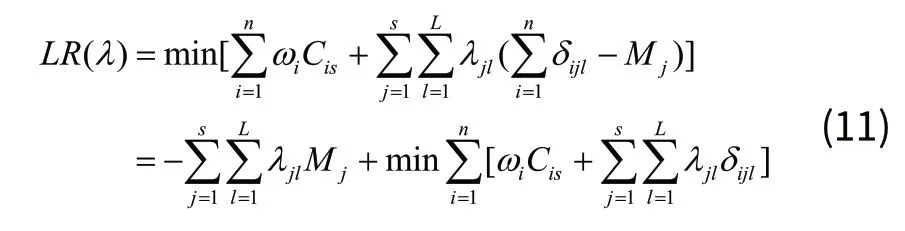
满足约束(3)～(10)和：

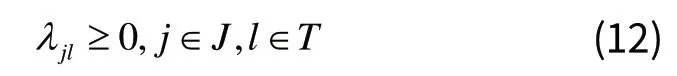
通过不断的逼近对偶问题的上界得到拉格朗日对偶问题：

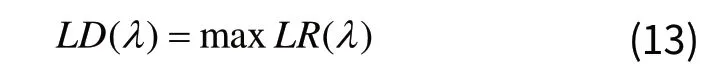
满足约束(3)～(10)和(12)。

当乘子给定时，式(11)中的前半部分是一个常数，将后半部分基于工件进行分解，得到多个工件级子问题，工件i 的工件级子问题可表示为：

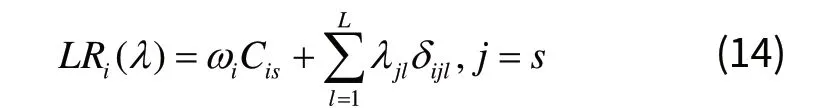
满足约束(3)～(10)和(12)。整理后得到：

因此， ( )LR λ 可归结为：

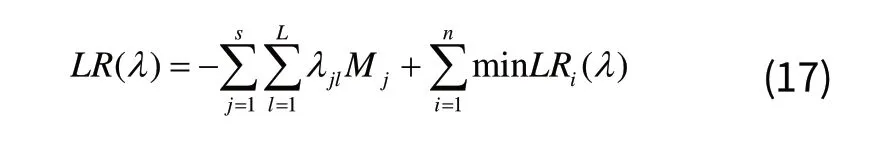
满足式(3)～(10)和(12)。

2.2 子问题的求解

利用反向动态规划来求解工件级子问题。当给定工件i和一组乘子时，利用以下递推公式来计算出工件i在各个阶段的累积函数值：

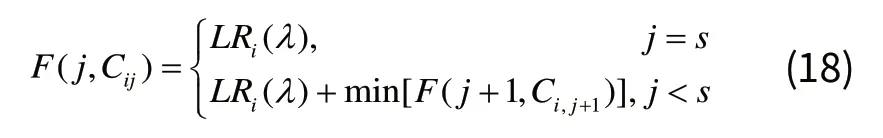
2.3 构造可行解

由于松弛了机器容量约束(2)，得到的松弛问题的解往往是不可行的，需要进行可行化，构造可行解的过程如下：首先根据得到的工件的完成时间计算出工件在各个阶段的开始加工时间表。在每个加工阶段，按照工件在该阶段的开始加工时间的增序进行排列，依次将工件安排在可利用的机器上；然后检查各个工件相邻阶段之间的等待时间是否满足要求，如果某工件在相邻两阶段之间的等待时间超过了给定的时间上限，则将该工件在前一阶段的开始加工时间后移，与后一个工件进行两两交换，直到前后两个阶段之间的等待时间满足要求为止。

2.4 更新拉格朗日乘子

采用次梯度算法来对拉格朗日乘子进行更新。主要步骤如下：

STEP1：迭代次数 1n= 时，初始化拉格朗日乘子及相关参数。

STEP3：更新乘子。根据下列式子更新拉格朗日乘子：

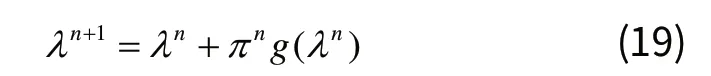
其中nπ 是n次迭代步长，nπ 通过下式计算得到：

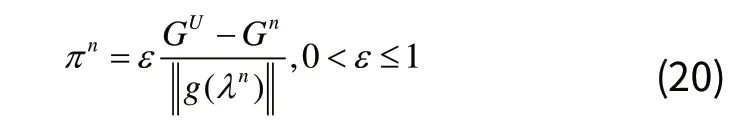
上式中GU是当前得到的最优的可行目标值的上界；Gn是n次迭代的 ( )LR λ 值；ε初始值设为1，Gn上升时保持不变，当Gn在若干次迭代中未发生变化时则取其一半。

STEP4：判断是否满足停止条件。若对偶间隙小于一个很小的数或达到了最大迭代次数，程序停止；否则返回STEP2进行下一次迭代。

图1为拉格朗日松弛算法流程图。

图1 拉格朗日松弛算法流程图

3 仿真结果及分析

为了对所提出的拉格朗日松弛算法进行可行性和有效性的验证，采用MATLAB对上述拉格朗日松弛算法进行编程，并在Intel(R) Core(TM) CPU 3.2GHz的计算机上运行。

分析表1～表3中的数据可以看出：

1）对于同一问题规模（当工件数和阶段数一定时），随着并行机器数的增加，可利用的机器资源增加，运行时间有所减少，对偶间隙也得到了改善；

2）对于同一规模问题，随着相邻阶段之间的等待时间的增大，算法的运行时间相应加长，得到的解质量略有下降（对偶间隙略有增加）。即和对解的质量（对偶间隙）的影响很小，由此说明所设计的拉格朗日松弛算法对于不同的等待时间均能得到较好的近优解。

3）对于不同规模问题而言，时算法的运行时间随之增加。且当由5增加到10时，运行时间有较大幅度的增加。

图2为不同工件数在加工阶段数为5，各个阶段的机器数为4，等待时间为10的情况下对偶间隙随迭代次数变化趋势图，三条曲线分别反应了工件数为10，20和40时的对偶间隙变化，从图中可以看出：

1）所设计的拉格朗日松弛算法在迭代前期有较好的收敛速度，随着迭代次数的增加，收敛速度逐渐减缓并最终趋向于收敛。

2）在加工阶段和机器数量相同时，在同一迭代次数下，规模较大的问题的对偶间隙比规模较小的问题的对偶间隙要相对大一些，即规模较小的问题所得到的解的质量相对好一些。

表1 n=10的仿真结果

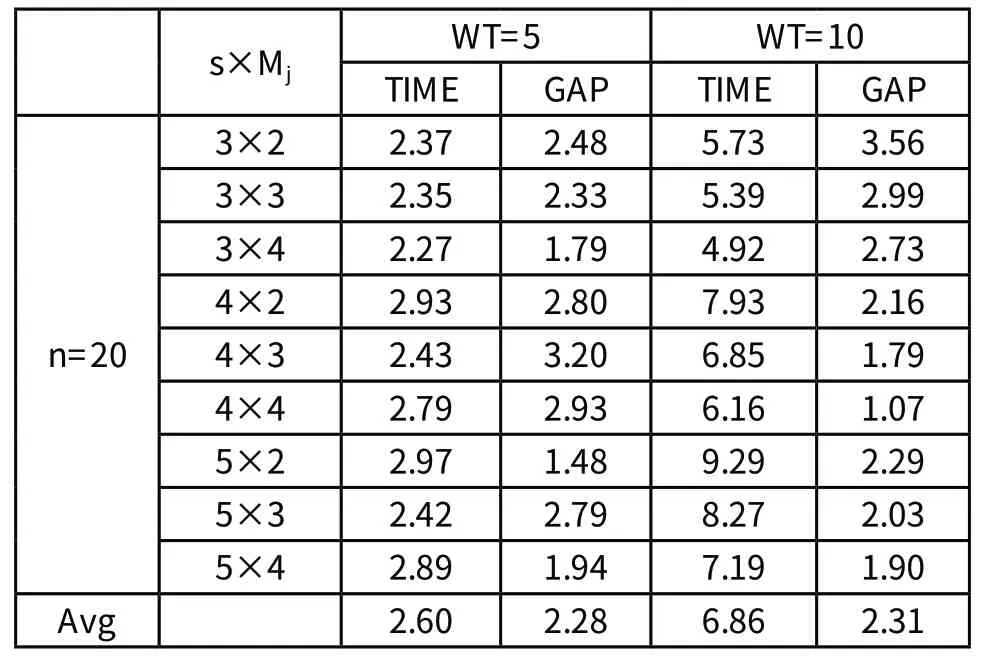
表2 n=20的仿真结果

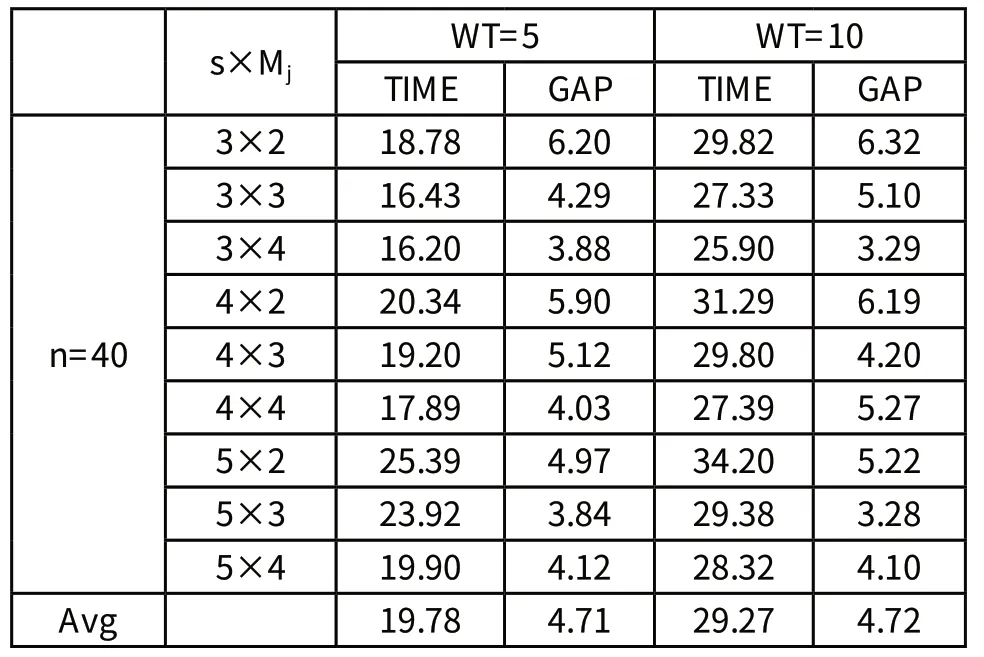
表3 n=40的仿真结果

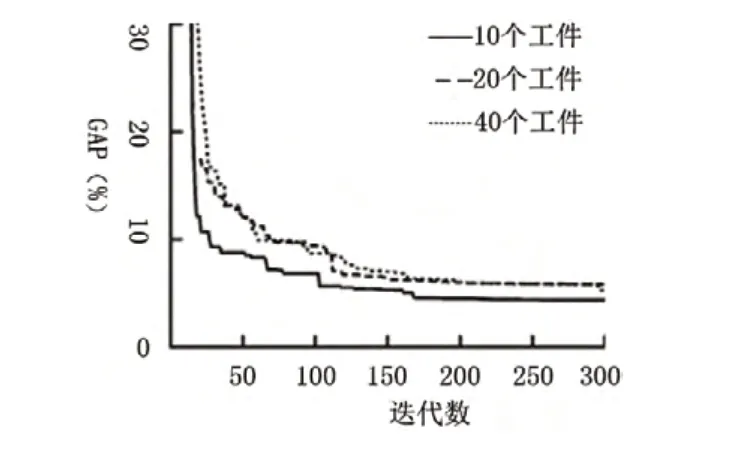
图2 不同工件数时对偶间隙随迭代次数变化趋势

综合上述分析可以看出，本文所设计的拉格朗日松弛算法能够在较短的时间内产生较好的近优解，可以用于等待时间受限的混合流水车间调度问题中。

4 结束语

本文针对由于生产过程中的高温连续性等要求而产生的等待时间受限的混合流水车间问题进行问题建模和算法的研究。首先建立了等待时间受限的混合流水车间调度问题模型，然后在此基础上设计相应的拉格朗日松弛算法来进行求解。该算法通过将机器容量约束松弛到目标函数中，进而将得到的松弛问题分解为一系列易于求解的工件级子问题来进行求解，并利用动态规划算法来求解子问题，然后对得到的松弛问题的解利用一种启发式算法来进行可行化，并通过次梯度算法来不断更新乘子。最后对设计的算法进行仿真验证，测试结果表明所设计的拉格朗日松弛算法能够在较短的时间内产生较好的近优解。

[1] 王凌,周刚,许烨,等.混合流水线调度研究进展[J].化工自动化及仪表,2011,38(1):1-8.

[2] Gicquel C,Hege L,Minoux M, et al. A discrete time exact solution approach for a complex hybrid flow-shop scheduling problem with limited-wait constraints[J].Computers & Operations Research, 2012,39(3):629-636.

[3] Liu S Y, Cui J S, Li Y. Heuristic-Tabu algorithm for hybrid flowshop scheduling with limited waiting time[A].Wuhan:Proceeding of the International Symposium on Computational Intelligence and Design[C].2008:233-237.

[4] 尹兆涛,李铁克.考虑交货期和等待时间受限的HFS调度问题的混合算法[J].工业工程,2009,12(1):79-83.

[5] 王长涛,刘春光,胡平东,等.混合流水车间等待时间优化研究[J]. 沈阳建筑大学学报(自然科学版),2012,28(2):368-374.

[6] 肖拥军,李铁克,尹兆涛.考虑特殊时间约束的混合流水车间调度[J].计算机工程与应用,2010,46(8):205-207,231.

[7] Gupta J N D. Two stage,hybrid flow-shop scheduling problem[J]. Journal of Operational Research Society,1988,39(1):359-364.

[8] 轩华,唐立新.实时无等待HFS调度的一种拉格朗日松弛算法[J]. 控制与决策,2006,21(4):376-380.

[9] 杜书魁.需准备时间的FFS调度的一种拉格朗日松弛算法[J].科学技术与工程,2012,12(6):1272-1277.

[10] 张其亮,陈永生.带有阻塞限制的混合流水车间调度问题的混合粒子群求解算法[J].信息与控制,2013,42(2):252-257.

[11] 屈国强.瓶颈指向的启发式算法求解混合流水车间调度问题[J]. 信息与控制,2012,41(4):514-521,528.