一种多时码雷达信号及其特性分析
谭 龙,姜秋喜,潘继飞
(电子工程学院,合肥 230037)
0 引 言
近年来,随着低截获概率雷达的不断发展,各种低截获技术也得到不断提高,现今主要的低截获技术手段有功率管理、波形设计、雷达组网技术以及环境的利用等[1]。其中对信号波形的设计仍是最具实效的手段之一[2]。
目前已有的波形技术有调频连续波(FMCW)[3]、频移键控(FSK)、相移键控(PSK)[4]、噪声技术[5]等。其中PSK波形因其具有大的带宽,可以获得高距离分辨力的波形,同时还能为雷达提供大信噪比处理增益等优点而在近年来成为活跃的研究主题。多相相移技术在雷达波形的设计上是灵活多样的,常用的PSK技术有巴克码(Barker)序列和弗兰克(Frank)码,以及P1、P2、P3、P4码等,每种编码都能作为有用的LPI连续波相移键控技术进行使用,这是因为凭借其宽带特性,可以迫使截获接收机一开始就必须加大接收带宽,从而降低了截获灵敏度,给侦察截获增加了难度,即提高了雷达信号的低截获性能[1]。
本文着重对PSK技术中一类在国内少有研究的多时码信号进行了探讨,重点分析了该信号的时频域特性,研究了该信号在低截获性能上的优越性。
1 多时码信号基本模型
多相码信号是对步进频率或线性调频波进行近似得到的,通过对基础波形的近似,从而反映出相位步进的变化,其所有给定的相位状态所占用的时间是相同的,为一个常量。而多时码信号对基础波形的量化是建立在用户所选择的相位状态数的基础之上,即每个相位状态占用时间在整个波形的持续时间内是不断变化的[6]。
目前,已经验证得到的有T1(n),T2(n),T3(n),T4(n)4种多时码波形,其中T1(n),T2(n)是由步进频率模型产生的,T3(n),T4(n)是由线性调频波形近似得到的,其中n为基础波形近似的相位状态数。
多时码雷达信号的模型为:

式中:A为信号幅度;f c为基础波形载频;φT(t)为多时序列的折叠相位相对于时间的表达式。
对T1(n),T2(n),T3(n),T4(n)4种码型,其各自的相位时间为:

式中:INT[]为取角函数;k为码序列的段数;j=0,1,2,3,…,k-1,为步进频率波形的段号;n为对应码序列的相位状态数;T为整个编码持续时间;tm为调制周期;ΔF为调制带宽;t为时间[6]。
2 多时码信号的产生机理及时频域分析
4种多时码信号的产生机理都是相似的,只要理解了其中一种,其余3种都能以此为基础推导出来。本文仅对T1(n)码的产生机理及时-频特性进行简单分析。
首先对T1(n)码信号的产生机理进行简单介绍。设其相位状态数为n,故对其进行量化后得到Δφ=2π/n,这里以n=3为例,即步进频率波形的相位增量为120°,一旦超过120°频率稳定一段时间,直到下一个120°界限为止。这里假设整个编码周期长度(编码持续时间)为T=16μs,因为T1(n)是在步进频率的基础上得到的,故将其分成k段,此例中令k=4,即每段持续时间为4μs,则相邻段的步进频率为1/(4μs)=250 Hz。其具体变化过程如图1(a)所示(根据需要可以灵活设置相位状态数n和段数k)。在第1段的4μs内为零频率,相位在零处为常数;在第2个4μs的持续时间内累加了一个完整的周期(360°);在第3个4μs的持续时间内又累加了2个完整的周期(720°);在第4个4μs的持续时间内再累加了另外3个完整的周期(1 080°),最终累加的总相位为2 160°。将步进频率折叠相位量化为0°,120°和240°后如图1(b)所示。

图1 T 1(n)码相移特性
为帮助理解,再对T1(n)码的相位调制公式进行简单推导。这里人为地将信号编码的持续时间16μs分成k=4段,则相位调制的表示式为:
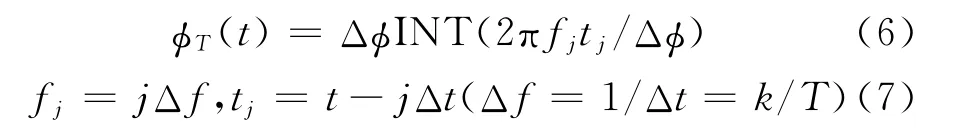
式中:Δφ表示对相位进行量化,其值等于2π/n;2πf jt j为时刻t的瞬时相位;f j,tj分别为第j段的频率和时间。
代入化简得到其未折叠时的表达式为:
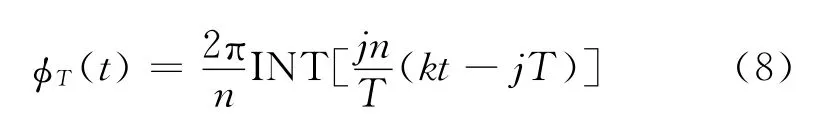
再对其进行取模运算,得到折叠后的表达式为:

为更直观地观察信号步进频的变化情况,用φ′表示前面j-1段相位的累积和,其计算如下:

即前j段的相位表示为:

由上述T1(n)码信号的产生过程及公式推导,为便于观察,将信号频率降到中频进行仿真,设信号的脉宽为16μs,载频为20 MHz,可得信号的时域、 频域特性如图2所示[7-8]。

图2 信号的时频域特性
图2中由信号的频谱看出,信号的带宽得到了展宽。从时域波形观察可知,信号每个相位状态的持续时间不同,所以随着时间的推移,信号相位在什么位置改变也是难以预测的,这就使得该信号波形的复杂性较高。而且,相位状态数n的增加使得信号波形的复杂度也随之进一步提高。
3 多时码信号特性仿真分析
3.1 多时码信号的自相关和模糊函数特性
模糊函数是雷达信号理论中一个重要的概念,是研究和设计雷达信号波形的有效数学工具。其定义为[9]:

将式(1)代入得到多时码信号的模糊函数:

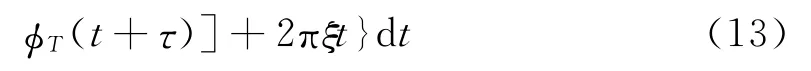
式中:φT(t)有式(2)~式(5)4种形式,这里仍以T1(n)为例。
当ξ=0时,即得到信号的自相关函数。设信号参数的取值同上,T=16μs,f c=20 MHz,k=4,可以得到多时码信号的模糊函数图及自相关图如图3所示,tb为子码周期。
由图3(a)可以看出,当相位状态数为3时,其脉压输出特征出现了预期的图钉型的模糊图,具备了雷达信号的探测功能。但同时由图3(b)也能看出,得到的自相关图多普勒旁瓣较高,峰值旁瓣电平出现在主瓣附近,约为-10 dB,离散旁瓣电平在-20 dB左右,不是非常理想。下一步,通过选择适当的算法和信号处理方式来提高信号的旁瓣特性,将是研究此类信号的关键。
为观察随相位状态数的改变而呈现的差别,将n值增加到6后观察图4。

图3 n=3时的T 1(n)信号的自相关和模糊图
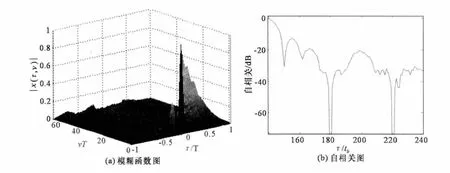
图4 n=6时的T 1(n)信号的自相关和模糊图
由图4(a)可知,随着多时序列相位状态数的增加,其旁瓣性能也可得到相应的改善。具体值如图4(b)所示,最大旁瓣电平约出现在-13 d B处,离散旁瓣电平在-30 d B上下。
3.2 多时码信号的低截获特性
设发射信号(即接收机接受到的信号)的脉冲宽度为τi,经脉冲压缩后的有效宽度τo,则脉冲压缩比D的定义式为D=τi/τo,又因为τo=1/Bo,所以D=τi B o,即压缩比等于信号的时宽带宽积。如果压缩网络是无源的,由能量守恒原理,它本身不消耗能量也不加入能量,则有:

式中:D=τi/τo=Po/Pi;Pi为输入脉冲的峰值功率;Po为输出脉冲的峰值功率。
由公式可知,输出脉冲的峰值功率Po增大了D倍[10]。对于扩频信号,它将信号的频谱进行了展宽,这就势必使各频谱成分的幅度下降,使信号的功率谱密度降低。因此,利用脉冲压缩原理可以降低接收所需的功率,即能用较小的信号发射功率达到预期的目的,这就是扩频信号具有低截获概率的原因。换句话说,大时宽带宽积信号具有低截获特性[11]。
为说明多时码信号在低截获波形设计上的灵活性和优越性,将其与相位编码信号进行比较。一个脉宽为T的宽脉冲分解成N个宽为τ的子脉冲,通过改变每个子脉冲的相位可以增加带宽(因为相位随时间的变化率是频率)。二相编码信号的带宽为B≈1/τ=N/T,信号的脉冲压缩比D或时宽带宽积等于子脉冲的数量N,即D=TB=TN/T=N。所以采用长的二进制序列,就能得到大的时宽带宽积的编码脉冲压缩信号。巴克码是一种特殊的二进制码,只有它能使编码信号自相关函数峰值旁瓣(PSL)的幅度都小于或等于1/N,如图5所示(巴克码信号T=16μs,f c=20 MHz)。

图5 不同长度巴克码信号的归一化自相关图
但目前为止,经过验证的最长巴克码只有13位,因而巴克码的最大脉冲压缩比为13。这对于脉冲压缩雷达的应用来说,是一个相对较低的值,其他实际的二进制编码可以是任意长度,但它们的旁瓣特性又不能尽如人意。对于多相码信号,其码长或脉冲压缩比也满足D=N,虽然通过增加相位状态数可以用来提高信号的时宽带宽积,但这样做的代价会使得系统变得更加复杂,难以实现[12-13]。
对于多时码信号,仍以T1(n)为例,由信号产生机理可知,整个编码持续时间为T,波形被分成k段,相位状态数设为n,则总带宽B为:

观察式(16),信号的时宽带宽积与相位状态数n无关,即只需极少的几个相位状态,通过控制段数k,便可以得到任意时宽带宽积的信号,这就为灵活设计低截获波形提供了方便,如图6所示。

图6 不同k值多时码信号的归一化自相关图
综上所述,为了得到预期的大的时宽带宽积,相位编码信号必须付出相应的代价,而多时码信号则灵活简便,这是传统调制信号所无法比拟的。
4 结束语
本文对多时码信号进行了分析研究,主要对该信号的相位模型和产生过程进行了详细的阐述;同时仿真分析了信号的时频域特征,从时域和频域的角度观察分析了信号的性能;并通过模拟产生信号的自相关图和模糊函数图,进一步说明了该信号的探测性能;最后通过讨论脉冲压缩比D(时宽带宽积)将相位编码信号和多时码信号进行了比较,说明采用这种信号形式,可以灵活设置信号的时宽带宽积,在扩展雷达信号频谱的同时,降低雷达信号的峰值发射功率,改善信号的旁瓣性能,是一类有效的低截获概率雷达信号。
[1]Pace Phillip E.Detecting and Classifying Low Proba-bility of Intercept Radar[M].Boston,America:Artech House Inc,2009.
[2]David Lynch Jr.Introduction to RF Stealth[M].Boston,America:SciTech Publishing Inc,2004.
[3]Fu J S,Ke Y.Anti-jamming aspects of linear FM and phase coded pulse compressions by simulation[A].CIE International Conference of Radar Proceedings[C],1996:605-608.
[4]袁东风.FSK和PSK信号特征研究[D].北京:北京邮电大学,2011.
[5]Guosui L,Hong G,Xiaohua Z,Weimin S.The present and future of random signal radars[J].IEEE Aerospace and Electronic Systems Magazine,1997,12(10):35-40.
[6]Fielding J E.Polytime coding as a means of pulse compression[J].IEEE Transactions on Aerospace and E-lectronic Systems,1999,35(2):716-721.
[7]庞建丽.典型信号傅里叶分析及仿真实现[J].现代电子技术,2011(13):78-80.
[8]黄植功.基于 MATLAB的连续信号频谱分析[J].广西物理,2009(3):53-56.
[9]孙亚东.雷达信号模糊函数理论研究与仿真[D].武汉:武汉理工大学,2007.
[10]张明友,汪学刚.雷达系统[M].第3版.北京:电子工业出版社,2011.
[11]史林,彭燕.一种低截获概率雷达信号及其信号处理[J].现代雷达,2003(6):26-28.
[12]陈浩.二相编码信号特征分析[J].舰船电子对抗,2006(3):22-24.
[13]邓振淼,刘渝.多相码雷达信号调制方式识别[J].数据采集与处理,2008(3):265-269.

