关联规则挖掘在电子对抗目标分析中的应用
李 政,祝 利,韦 伟
(电子工程学院,合肥 230037)
0 引 言
信息化战场上的电子对抗目标之间、电子对抗目标与其它武器系统、作战行动之间往往是相互联系的。掌握这种关联关系,可以更加准确地把握电子对抗目标的活动规律,并对其活动进行预测,为电子对抗作战和其它作战预案的制定提供依据。
对于电子对抗目标的关联分析,目前主要基于先验知识的人工判断。随着电子对抗目标增多及其活动规律日益复杂,上述方法愈加难以实现。如何从海量侦察数据中使用自动化方法对电子对抗目标进行关联分析,成为一个亟待解决的问题。
1 关联规则挖掘
关联规则挖掘是数据挖掘的一个重要领域,是模式挖掘的一种基本形式,其目的是挖掘和搜索数据集中反复出现的联系。关联规则有些是常识、经验性的,而另一些则是启发性的。
随着可分析数据量的增大,关联规则挖掘越来越受到重视。例如在商业领域,从大量交易数据中发现相关联系,可以为产品促销、超市货架规划、顾客购买习惯分析提供决策支持。
1.1 相关概念
1.1.1 关联规则
设I={i1,i2,…,im}为项集,D是数据库事务的集合,其中每个事务T是一个非空项集且T⊆I。设A是一个项集,包含于事务T中。关联规则形如A⇒B,其中A⊂I,B⊂I,A≠∅,B≠∅,并且A∩B≠∅[1]。关联规则表示某一类或几类项目与另一类项目之间存在的单向影响关系。关联规则的典型案例是购物篮模型,例如通过对顾客购物篮内货物的分析,可以发现牛奶和面包等某几种货物总是频繁地一起出现。这个例子中,“购买牛奶的顾客更倾向于买面包”即是一条关联规则,可以表示为:

1.1.2 支持度与置信度
支持度s表示A∪B在事务D中所占的百分比,即s(A⇒B)=P(A∪B)。置信度c表示D包含A的事务的同时包含B的事务的百分比,即c(A⇒B)=P(B|A)。支持度和置信度是对于规则的2种度量,分别表示规则的普适程度和确定程度。最终挖掘的结果与挖掘算法中最小支持度与置信度阈值的取值有很大关系,若取值过高,难以发现关联规则,若取值较低,关联规则的参考价值就会大打折扣,且其数目会过多。在上述“牛奶与面包”的例子中,若关联规则的支持度为5%,置信度为60%,可以表示为:
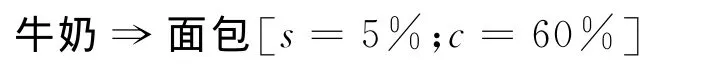
1.1.3 频繁项集
若项集I满足设定的最小支持度阈值,则称I为频繁项集。上述例子中,由于牛奶和面包总是频繁地一起出现在购物篮中,若其满足相应的支持度与置信度条件,则<牛奶,面包>构成了一个频繁项集。根据支持度与置信度的定义,置信度与支持度有如下关系:

式中:s_count()为支持度计数。
根据式(1),A⇒B的支持度与置信度很容易从A、B和A∪B的支持度计数中得出,也就是说一旦确定A、B和A∪B的支持度计数s_count(A)、s_count(B)和s_count(A∪B),就能确定关联规则A⇒B或B⇒A。因此,关联规则的挖掘可以最终归结为确定频繁项集。
1.2 典型算法
关联规则挖掘一般可以分为2个步骤:第一是找出所有的频繁项集,第二是由频繁项集确定关联规则。典型的关联规则挖掘算法基本上按照上述步骤进行挖掘。
1.2.1 Apriori算法
Apriori算法于1994年由Agrawal和R.Srikant提出,是一种多候选产生类布尔型关联规则挖掘算法。由于该算法采用逐层搜索的迭代方法,每次找出一组频繁项集就要对数据进行一次扫描,为了减少计算量,采用“频繁项集的所有非空子集也是频繁项集”这一先验性质压缩扫描空间[2]。
1.2.2 FP-growth算法
由于Apriori算法需要产生大量的候选集以便从中寻找频繁项集,并需要重复多次扫描数据库,影响了算法的效率。针对这些问题,Jiawei Han于2000年提出频繁模式增长(FP-growth)算法。该算法首先将数据集构建成1棵频繁模式树(FP-tree),再基于频繁模式树对频繁项集进行挖掘。该算法仅需对数据集进行2次完整的扫描,且可以明显地压缩所要搜素的数据集的大小,因此得到了广泛应用。1.2.3 序列规则挖掘算法
序列规则是在普通关联规则基础上添加时间信息,对于每一个时间段,都有在该时间段收集到的数据与之对应,即有多少时间段就有多少数据集[3]。在序列规则挖掘中,时间段代替了普通关联规则挖掘中的“购物篮”。典型的序列规则挖掘算法有基于FP-tree的高效数据流频繁项集挖掘算法FPStream和针对滑动时间窗口的FTP-DS频繁项集挖掘算法等[4]。
2 基于关联规则的电子对抗目标关联分析
战场上,电子对抗目标之间、电子对抗目标与武器系统及作战行动之间的关联关系表现为2种模式:
一是电子对抗目标、武器系统、其它作战力量同时活动,体现出协同关系,例如多部雷达同时对同一目标进行探测;
二是电子对抗目标、武器系统、作战力量依次活动,体现出时序关系。例如防空导弹对敌机进行拦截时,预警探测雷达往往先于制导火控雷达工作。
对于这2种模式,分别对其采用静态关联规则挖掘算法和序列规则挖掘算法进行分析。
2.1 静态关联规则挖掘
针对电子对抗目标、武器系统、作战力量同时活动的情况,采用包含时间信息的FP-growth算法对其中的关联规则进行挖掘。挖掘过程主要有以下步骤:
(1)数据处理
常规的FP-growth算法的数据中并没有时间信息,为了体现目标同时出现的情况,将常规算法中的事务T设为时间段,即用时间段代替“购物篮”,将时间段尽量设小,以体现目标出现的同时性。
电子对抗侦察数据中重要的参数是目标的出现和消失时间,对其进行关联规则挖掘时只需关注目标编号和目标活动时间这2个参数。在此将侦察数据整理成表1所示的形式,即每个时间段及在该时间段内出现的目标编号。
表1的时间段设定成1 s。需要注意的是,目标编号处不仅可以是电子对抗目标,也可以是其他武器系统或作战行动。
(2)确定初始频繁项集
对数据集进行完整扫描,对目标Ii出现的次数计数,确定支持度计数不小于最小支持度阈值的目标集合L,并按支持度计数递减排序。这里举例设:


表1 数据格式
(3)构造FP-tree
首先创造树的根节点,记为n。对数据集进行扫描,创建树的分枝。例如t1时间段包含I1、I2、I53项,其在L中的次序是I2、I1、I5。将I2作为根节点的子节点链接到n,I1链接到I2,I5链接到I1。t1时间段包含I2、I4项,其中I2链接到n,I4链接到I2。由于之前已经创建节点I2,因此I4与t1时间段共享节点I2。依此法构造FP-tree(如图1所示),就可将频繁项集挖掘问题转化为FP-tree挖掘问题。

图1 FP-tree
(4)挖掘频繁项集
FP-tree的挖掘过程如下:首先由长度为1的频繁模式(初始后缀模式)开始,构造其条件模式基,然后构造其FP-tree并对其进行递归挖掘。
以上面构建的FP-tree为例,首先考虑I5,I5出现在2个分支中,分别为路径 〈I2,I1,I5:1〉和〈I2,I1,I3,I5:1〉。以I5为后缀,其前缀路径为 〈I2,I1:1〉和〈I2,I1,I3:1〉构成I5的条件模式基。使用上述条件模式基构建 FP-tree,该树仅具有 〈I2:2,I1:2〉1个分支,因为I3的支持度计数不满足最小支持度阈值。因此,该路径包含的频繁模式为依此法对其它目标进行频繁项集挖掘,即可确定所有项集模式。
(5)确定关联规则
挖掘出所有频繁项集后,可以直接由其产生满足最小支持度和置信度的强关联规则:
首先,对于每个频繁项集l产生其所有非空子集m。
其次,对于非空子集m,如果tmin_c,则 产 生 关 联 规 则m⇒(l-m)。 其 中s_count()为支持度计数,tmin_c为最小置信度阈值。
(6)评估关联规则
由于置信度有时不能完全反应A、B相关性的实际强度,尤其是支持度阈值较低或关联规则较长时。因此必须采用其它指标对关联规则进行评估,在这里选用提升度指标:

若提升度小于1,表示A、B是负相关,而提升度大于1则表示A、B正相关。对前面挖掘出的关联规则使用提升度进行评估后,即可得到最终有价值的关联关系。
2.2 序列关联规则挖掘
序列挖掘是对相对次序或时间出现频率高的模式进行发现的方法。上述对于电子对抗目标的静态关联规则挖掘虽然数据集包含时间信息,但在挖掘中没有体现,挖掘的内容是电子对抗目标、武器系统、作战单位同时活动时的关联规则。序列关联规则挖掘在上述方法的基础上加上了时间因素,能够反映电子对抗目标、武器系统、作战单位依次活动时的规律。
序列挖掘采用和关联规则挖掘类似的过滤算法,所需的数据格式与静态关联规则挖掘算法相同,可采用R语言和Statistica等软件进行实现。除支持度、置信度、提升度等指标外,进行关联模式挖掘需要注意的还有最大间隔指标,该指标表示关联规则中2个目标出现时间的最大间隔[5]。该值若设置过大,则难以体现目标的关联性。
3 关联规则挖掘仿真与分析
3.1 基于FP-growth的静态关联规则挖掘的仿真
下面以2 220条模拟侦察数据进行仿真。该批数据中共有A、B、C、D、E5个电子对抗目标,时间以1 s为1段,共计2 220 s,分别以支持度5%、10%、15%、20%,置信度60%进行挖掘,仿真发现支持度为10%时可以获得一定数目有价值的关联规则,剔除关联规则中提升度不大于1的数据,得到关联规则如表2所示。

表2 部分挖掘的关联规则
从表格中可见,目标B、C关联性较强,目标C出现时B出现的频率以及B出现时C出现的支持度都达到了65%以上。另外,目标A、B出现时目标C出现的次数虽然不多,但置信度和提升度最高,可见该规则具有很高的参考价值,在侦察活动中若发现A、B目标同时活动,应重点关注C目标。将目标活动情况进行可视化显示(如图2所示),从中可以发现B、C目标活动规律的关联性十分明显,但是对于其它关联的活动规律难以通过人工判断进行挖掘,而采用FP-growth静态关联规则挖掘算法就能很好地对其进行分析,体现出该方法的有效性。

图2 目标活动规律
3.2 序列关联规则挖掘的仿真
仿真时使用R语言arulesSequences程序包对一批模拟侦察数据进行挖掘,数据集中有A、B、C、D、E、F、G、H共8个电子对抗目标,每个时间段划分为1 min,支持度分别设为5%、10%、15%、20%,置信度为60%,最大时间间隔为10 min,仿真发现支持度为20%时可以获得一定数目有价值的关联规则,如表3所示。

表3 部分挖掘的关联规则
从表中结果可见,目标F在目标A之后10 min之内出现的支持度达到了45%,在侦察中若发现目标A活动,应及时在目标B的频段对其进行控守。序列{B,F}、{A,B}支持度也较高,值得关注。
4 结束语
本文针对电子对抗目标之间、电子对抗目标与武器系统及作战行动之间的2种关联模式,分别采用了包含时间信息的FP-growth静态关联规则挖掘算法和序列关联规则挖掘算法进行挖掘。仿真结果表明,通过上述方法可以揭示电子对抗目标之间、电子对抗目标与武器系统及作战行动之间同时活动和依次活动2种关联关系,能够为电子对抗及其它作战行动提供决策参考,具有一定的实用价值。
[1]Jiawei Han.Data Mining Concept and Techniques[M].北京:机械工业出版社,2012.
[2]Rakesh Agrawal,Ramakrishnan Srikant.Mining sequential patterns[A].Proceedings of The Eleventh International Conference on Data Engineering[C].Washington D C,USA:IEEE Computer Society,1995:3-14.
[3]王星.大数据分析:方法与应用[M].北京:清华大学出版社,2013.
[4]马青霞,李广水,孙梅.频繁模式挖掘进展及典型应用[J].计算机工程与应用,2011,47(15):138-142.
[5]闫明月,侯忠生,高颖.一种面向布尔时间序列的关联规则挖掘算法[J].控制与决策,2012(10):1147-1151.

