刚构桥桥墩计算长度系数的计算方法研究

■黄锦春

（福州市规划设计研究院，福州 350002）

1 引言

在桥梁设计计算中，验算受压高墩的承载力、墩顶位移等均涉及到桥墩计算长度l0。计算长度l0的几何意义是：中心压杆失稳后，挠度曲线上两个反弯点（弯矩为0）的距离；物理意义是：各种支撑条件的中心受压杆，其临界荷载与一两端铰支中心受压杆的临界荷载相等时，两端铰支中心受压杆的长度。实际应用中，引入计算长度系数，它与杆端的支撑情况有关，通过公式l0=1 求解计算长度，其中l 为支点间长度。

关于墩的计算长度系数μ 的取值，《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTGD62-2004）规定：当构件两端固定时，取0.5；当一端固定一端为不移动的铰时，取0.7；当两端均为不移动的铰时，取1.0；当一端固定一端自由时取2。对于桥墩复杂的边界条件，以上四种情况无法概括完全。工程上一般根据经验验算，如果系数取值与实际情况相差太大，将造成不安全或者太保守，国内外规范对相关系数的规定如表1 所示。

表1 对各国规范系数对比

对于刚构桥，桥墩墩顶与梁体固结，桥墩下部不考虑桩基的柔度效应视为固结，由于墩有一定的柔度，且混凝土收缩、温度的影响以及在车辆等活载作用下的制动力会产生水平移动，移动量将影响计算长度，而移动量与墩顶的边界条件有关（如上部梁的刚度、相邻墩的抗推刚度等）。

2 数值分析方法

2.1 压杆稳定理论

在经典的材料力学理论中，压杆稳定临界力的欧拉公式表达为：

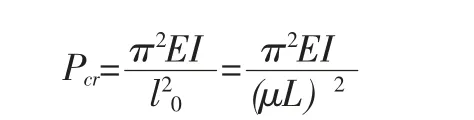
式中：L 为构件的实际长度；μ 为压杆的计算长度系数，对应着不同的边界条件有着不同的取值；EI 为构件的抗弯刚度。

欧拉公式的适用条件为：

（1）等刚度的弹性大柔度直杆；

（2）在小挠度范围内发生屈曲；

（3）屈曲时，轴力大小和方向均不变；

（4）不考虑几何非线性和材料非线性。

2.2 具有弹性支撑的压杆稳定分析

由于固结墩在温度力等作用下会产生位移，所以它并不是完全意义上的固结，考虑上部结构对墩的纵向约束，我们可以用一个横向弹簧约束来模拟它，计算模型简化图如图1 所示。

2.2.1 桥墩抗推刚度

纵向力按刚度集成分配给各个墩，墩自身的抗推刚度按下式计算：

式中：n 为一个桥墩的墩柱数；Ehi为墩柱抗压弹性模量；Ihi为毛截面惯性矩；h 为墩高，系数等为用“m”法计算桩基的有关系数，详见规范（JTG024-2004）附录六。

图1 计算模型简化图

2.2.2 墩顶的集成刚度

墩顶集成刚度计算主要是从整个体系上考虑相邻墩或支座对计算墩的墩顶约束刚度贡献，总体原则是在水平力作用下，上部结构所有的点水平位移相等，旁边墩对3 号墩刚度集成结果如图2 所示。

计算墩墩顶集成刚度为：为K合=K墩+K，K合可通过有限元建模求解，因此K=K合-K墩。

图2 3 号墩刚度集成

2.2.3 墩顶有弹性约束的桥墩计算长度公式推导

在欧拉公式的推导过程中结合能量法，对于满足边界条件的任何一个可能位移状态，求出势能δп，由势能的驻值条件δп=0 可以得到包含特定参数的齐次方程组。为了得到非零解，齐次方程组的系数行列式应为零，由此得到特征荷载值。临界荷载值Pcr是所有特征荷载值的最小值，将Pcr代入欧拉公式，求出墩的计算长度系数。

如图3 所示，x 位置的墩弯矩表达式为：

根据材料力学公式：EIy”=-M，即：

另n2=P/EI,则（2）式通解为：

图3 公式推导简化图

EI、L 都为定值，K 可以同通过上述方法求得：K=K合-K墩，解超越方程可得n 值。再根据欧拉公式可计算μ 值。

当墩顶自由时，K=0，tgnL=∞,nL=π/2，μ=2.

当墩顶固定式，K=∞,tgnL=nL，解得nl=4.49，μ=π/4.49=0.699，约等于0.7。

3 工程算例

福州市马尾大桥北互通连接机场二期左幅匝道桥在位于R=200m 的圆曲线上，有一联3×37m 的预应力混凝土连续箱梁，桥梁断面宽度10m，两边过渡墩与中间墩墩高均为28.5m，中间1 号、2 号桥墩采用墩梁固结方式，桥墩形式采用混凝土板式花瓶墩，桥墩采用C40混凝土，下部结构采用嵌岩桩基础。

通过有限元软件Madis 建立全桥三维杆系模型，如图4 所示,主梁、桥墩采用梁单元模拟，2 号与3 号墩墩梁固结，1、4 号过渡墩竖向约束，纵横向活动，桥墩参数如表2 所示。

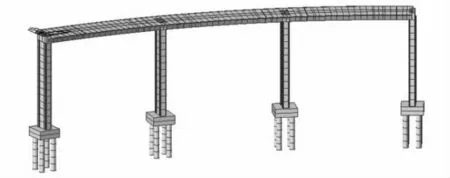
图4 全桥有限元模型

表2 各国规范系数对比

3.1 通过临界力与屈曲分析计算μ 值

通过欧拉公式直接求解，主要步骤如下：

（1）进行稳定分析，求得结构在自重作用下的失稳模态及稳定系数，计算结果如图5 所示。

图5 纵向失稳模态

（2）计算对应的失稳模式及临界荷载，计算结果如图6 所示。

图6 自重作用下墩顶轴力图

（3）根据欧拉公式计算结构的计算长度系数。

有限元模型计算得到，在自重作用下桥墩失稳时墩的轴力为8595kN，对应纵向失稳模态稳定系数λ=72。

计算值与美国规范1.2的数值偏差率2.5%，此方法计算简便，但没有模拟结构对墩顶支撑的影响，致使计算有一定的偏差。

3.2 考虑结构对墩顶刚度影响的方法

该方法考虑弹性支撑的压杆稳定分析，主要思路：

（1）在模型上加载一个水平纵向力，得到所需计算桥墩的水平力、水平位移得到该桥墩的总刚度K合。

（2）计算桥墩的刚度K墩，求出墩顶等代刚度K。

（3）按公式（4）计算μ 值。

在2号墩上加载一个水平力256kN，计算分析后得到2号墩顶的水平力及其位移，计算结果如图7和图8所示。

图7 2 号墩顶分配到的水平力

图8 2 号墩顶位移

2 号墩顶分配到146kN 水平力，对应的墩顶位移为6.14×10-3m，则2 号墩在整体体系中的总刚度：

K合=145.8/6.14×10-3=23749.7kN/m，

计算结果如表3 所示。

表3 计算结果表

将表格中数据代入公式（4），得到：

解得：KL=2.595，μ=π/2.595=1.21。

计算值与美国规范1.2基本一致。

4 结论

梁桥的桥墩的计算长度对桥墩的承载力与稳定性有非常重要的影响，本文从理论分析出发结合有限元程序提出两种相对比如适合工程人员计算桥墩长度系数的方法，经比对得到考虑结构对墩顶刚度影响的方法更加接近结构的实际情况，推荐采用该方法。

[1]牟晓光,曲春生.连续刚构桥墩计算长度系数的确定方法.公路,2013.

[2] 程翔云.高桥墩设计计算中的两个问题.重庆交通学院学报，2000,19(2).

[3]曾照亮.高墩计算长度探讨.中外公路，2008,28(5).

[4]谢钢城,谢新刚.墩顶为弹性支承的桥墩压杆的计算长度.公路,2013(1)

[5]雷博.梁式桥高墩计算长度研究.硕士论文，长安大学.

[6]李军,牟严松.梁桥高墩计算长度的一种计算方法.城市道桥与防洪，2009(6).