单颗磨粒的冲击磨损理论及实验研究*
宋 卫 袁巧玲 戴 勇 钟和冬
(浙江工业大学特种装备制造与先进加工技术教育部、浙江省重点实验室,淅江 杭州 310014)
随着航空航天、汽车等尖端领域的飞速发展,对零部件的加工精度和表面粗糙度的要求越来越高,传统的抛光方法很难满足零件的加工要求。磨粒流加工技术[1]作为新型超精密加工方法的典型代表,集流体力学、表面技术于一体[2-5],由于流体具有较好的仿形特性,能与被加工表面形成“无缝”接触,所以磨粒流广泛应用于现代先进制造业。螺旋式约束磨粒流抛光加工作为磨粒流加工方法的一种,对于长孔或长轴类精密工件的抛光加工具有独特的优势,其加工原理图如图1 所示,磨粒流在压力的驱动下从流道入口处进入封闭流道,在约束模块高速旋转运动的带动下,磨粒流在约束流道内加速达到湍流状态,高速运动的磨粒对工件壁面进行频繁无序的撞击实现对待加工表面的微切削,当装置沿轴向往复运动时就能实现对工件内壁完整抛光的目的。
螺旋式约束磨粒流加工流道内部属于旋转流场,分析旋转流场中磨粒对工件表面的冲击磨损特性为研究磨粒的运动轨迹、材料去除机理提供理论基础。近年来越来越多的学者通过数值模拟方法研究颗粒的冲击行为和磨损特性:Walker C I[6]等针对淤泥泵在工作时,由泥沙所产生的对泵体的磨损特性进行研究,首先对不同叶轮及侧道几何模型下的淤泥泵进行了研究,然后又分析了不同颗粒粒径、颗粒群及泵速对泵体磨损的影响;YabukiA[7]等通过分析圆形颗粒冲击固体表面时的运动特性,得到颗粒冲蚀的临界速度;唐学林等[8]基于数值模拟分析认为颗粒相速度相比于颗粒浓度,对固体表面的磨损具有更大影响;姚启鹏[9]等通过绕流磨损试验系统对水轮机内部的磨损做出了预估。
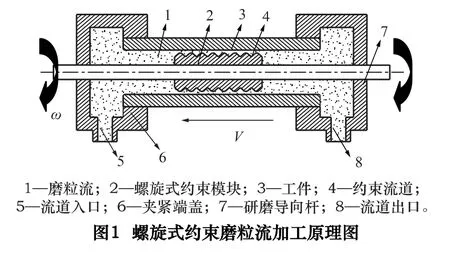
为研究旋转流场中单颗磨粒的磨损特性,本文结合磨损的相关理论,利用ANSYS 前处理器建立了磨粒冲击的3D 有限元模型,模拟单颗磨粒冲击工件表面时材料的变形机理和磨损情况,研究磨粒在不同的冲击速度和冲击角度下对工件表面材料磨损的影响。在实际加工中,流场的旋转速度大小对于磨粒的冲击行为影响较大,本文对旋转速度在颗粒撞击过程中所起的作用进行了理论和实验研究。
1 固体颗粒的冲蚀磨损理论
1.1 Finnie 微切削理论
Finnie.I 1958[10]年首先提出了塑性材料的微切削理论,他认为磨粒如同一把锋利的刀具,当它以一定速度划过靶材表面时,便切除材料使其产生磨损。该模型假定一颗质量为m 的多角形磨粒以速度v,冲角α撞击到靶材表面。研究得出冲蚀磨损量V 随入射角α变化的表达式为:
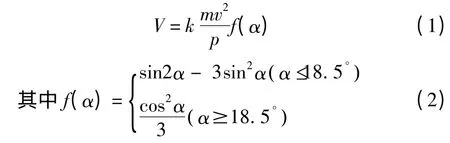
式中:k 为常数;p 为靶材流动应力。该模型很好地解释了多角形磨粒在小冲击角情况下对塑性材料的磨损规律,但对于塑性不典型的一般工程材料、冲击角较大(尤其对于冲击角为α=90°时)、非多角形磨粒(球形磨粒)的冲蚀磨损量误差较大,这与实际情况不相符合。
1.2 变形磨损理论
Bitter[11]将颗粒磨损机理分为两类:切削磨损和变形磨损。当磨粒以较小角度冲击靶面时,即碰撞主要发生在切向时,磨粒将对靶材表面进行刮削,这个过程称为“切削磨损”;而当靶材表面受到较大冲击角的冲击时,它将发生疲劳破坏,在后续颗粒的连续冲击之下将发生材料磨损,这个过程称为“变形磨损”。他认为材料的冲蚀磨损与粒子冲击靶材时的变形有关,并从冲击能量的角度出发,分析得出变形磨损量WD、切削磨损量WC与冲蚀磨粒的质量M、磨粒的速度v、冲击角α、切削磨损系数Q 之间的关系,该模型表达式如下:
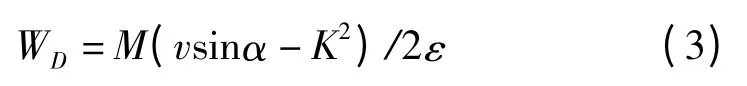
切削磨损量WC的表达式:
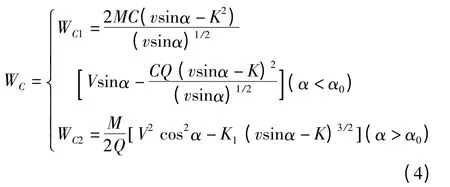
总磨损量可表示为变形磨损量与切削磨损量的和:

式中:α0为WC1=WC2时的磨粒撞击角度;C、K、K1为常数。变形磨损理论对塑性材料的冲蚀磨损现象做了较好的解释,但缺少支持的物理模型。
在实际加工过程中,合理估算材料的磨损量不仅要考虑磨粒大小、密度和形状等因素的影响,而且要考虑流体的速度粘性以及密度等参数对磨损量的影响[12-13]。为使磨损预估能应用于尽可能广泛的情况,美国大学的磨蚀研究中心提出了磨损预估模型,他们的磨损预估半经验公式表达式如式(6)。
磨损率ER 定义为单位壁面面积上的材料磨损质量与单位体积流量的磨料量之比,表达式为
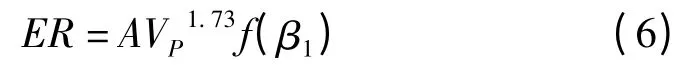
式中:A 为经验系数;Vp为颗粒冲击壁面的速度;β1为颗粒对壁面的冲击速度矢量与壁面切向的夹角;f(β1)为β1的函数,定义为
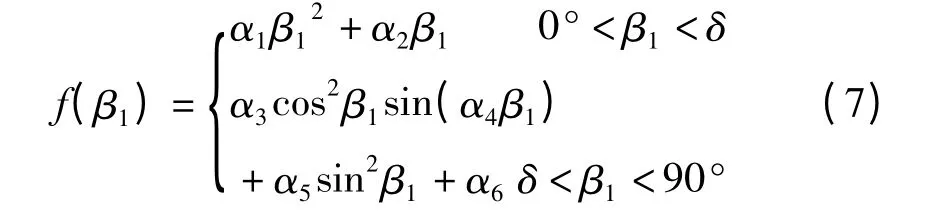
其中,A、δ、α1、α2、α3、α4、α5、α6是各经验系数值。
2 有限元分析
2.1 状态控制方程
在冲击动力学研究中,Gruneisen 状态方程常用来计算材料的冲击波效应。Gruneisen 这一状态方程可由两种方法定义压力体积的关系,从而确定材料是压缩还是扩张。
Gruneisen 方程定义压缩材料的压力P 为
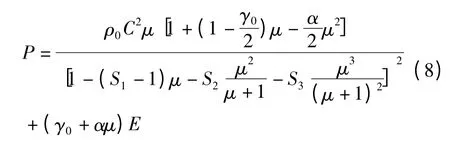
定义膨胀材料的压力P 为
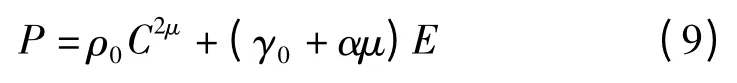
式中:C 是Vs-Vp曲线的截距;E 是初始动能;S1、S2和S3是Vs-Vp曲线的斜率系数;γ0是Gruneisen 常数;ρ是材料的初始密度;ρ0是材料被压缩后的密度;μ=ρ/ρ0-1;a 是γ0的一阶体积修正量。
2.2 有限元模型
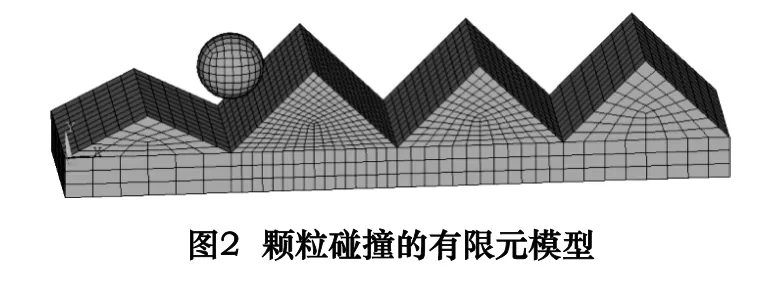
本文通过前处理器采用自顶向上的建模方法建立了完整的3D 颗粒冲击模型,有限元模型如图2 所示。为贴合实际,建立的冲击对象为高低起伏型的碰撞表面,冲击模型选用solid164 单元,solid164 为8 节点三维实体单元,单元的优点是支持大部分LS -DYNA 的材料算法,单元积分的优点是省时,并且支持大变形情况。为使计算出的结果接近实际问题,本文采用映射网格的方法对模型进行网格划分,为提高计算精度,对颗粒预期冲击的区域网格进行了加密处理,建模时将颗粒的形状理想为球形,整个冲击模型的单元总数为5874,其中被冲击工件的单元总数为5010,球形颗粒的单元总数为864,颗粒的半径为400 μm,工件下底板的尺寸为8000 μm ×2000 μm ×600 μm,表面上方建立粗糙不平的三棱柱波浪型表面,单个棱柱的竖直高度为1000 μm,棱柱的底面尺寸为2000 μm ×2000 μm,颗粒位于第二个V 型槽口正上方800 μm 的位置,对球形颗粒施加X,Y 方向的旋转全约束,底面设置Z方向的移动约束条件,工件四周施加非反射边界条件。
2.3 材料模型及参数的选择
材料模型和参数是影响模拟结果真实性最主要的因素,在冲击动力学数值模拟中应用最广泛的本构模型是Johnson-Cook 模型,是目前反映金属材料动态力学性能最成功的本构模型,一般表达式为:
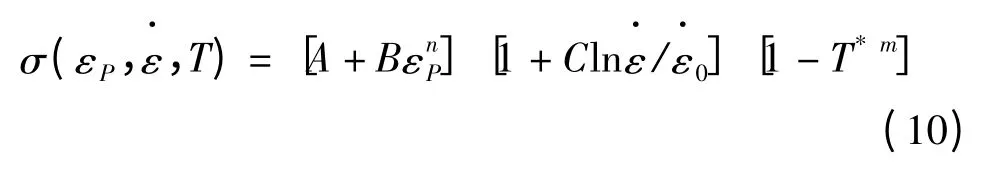
本文工件材料选用铝合金,材料参数值如表1 所示,球形颗粒选用刚性材料,参数如表2 所示。
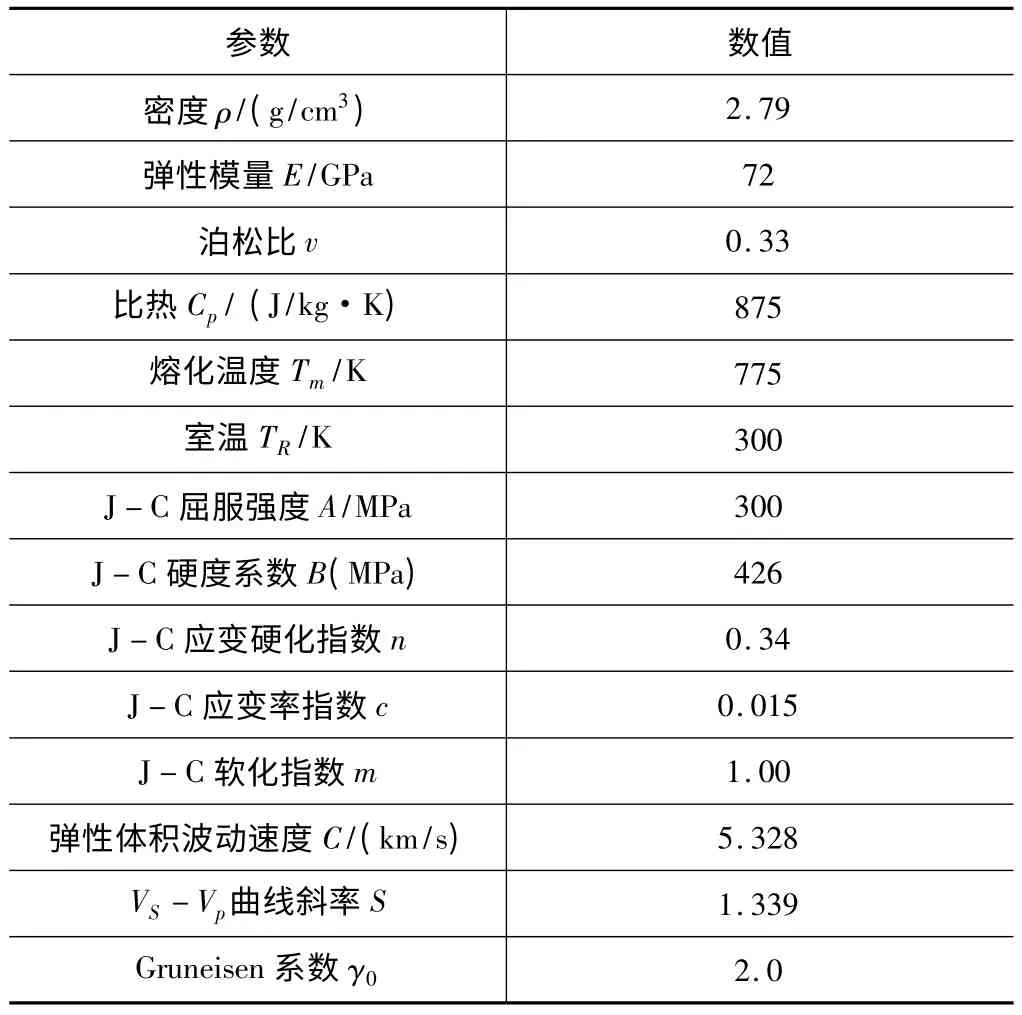
表1 JC 本构方程[14]及Gruneisen 状态方程参数

表2 球形颗粒材料参数
2.4 定义接触、求解时间
颗粒高速冲击工件表面属于侵蚀问题的研究范畴,接触类型选用面面接触和侵蚀接触类型,定义颗粒为目标体,工件为接触体,即完成了颗粒与工件表面的接触定义。求解时间的设置是关系到颗粒最终的冲击仿真效果。为减少计算时间,设定求解时间为2t,其中t 为磨料颗粒从开始降落到接触工件表面所需的时间。
2.5 求解及仿真结果分析
Bitter 的变形磨损理论表明材料的磨损分为变形磨损和切削磨损2 个阶段,并且磨损情况与粒子冲击工件的变形有关,当粒子冲击工件的应力值小于工件的屈服应力时,靶材只发生弹性变形;当粒子冲击工件的应力值大于工件的屈服应力时,工件表面将产生弹性和塑性2 种变形,在粒子连续冲击下形成磨损。本文设定旋转流场的速度为15 m/s,为简化计算,视颗粒随旋转流场一同做旋转运动,颗粒沿旋转方向的分速度为15 m/s,设定球形颗粒的初始冲击速度为30 m/s,求解时间为16 μs。图3 是球形颗粒与工件表面多次冲击的仿真图,初期冲击仿真图显示冲击区域的最大应力值超过了材料的屈服应力,材料已发生较为明显的塑性变形,材料的表面形成了1 个较大的压坑和变形唇,在颗粒与工件表面之间的界面两侧存在很大残余应力和应变,从第5 次冲击开始,撞击区域开始出现小块金属的剥落,随着冲击次数的累积,材料的去除量也有所增加,失效后的材料沿颗粒冲击方向发生较大的塑形变形延伸。仿真图还表明冲蚀磨损是1 个长时间孕育的过程,即颗粒冲击工件表面时只产生弹塑性变形而未出现材料磨损的现象,在颗粒的连续冲击损伤后才逐步产生材料的磨损。本文设定的颗粒冲击方向是沿工件表面的,材料去除以切削磨损占主要磨损形式。

在冲蚀磨损过程中,颗粒所具有的初动能是造成材料冲蚀磨损的动力源泉。图4 是球形颗粒分速度变化的曲线,颗粒的初动能可分为水平分速度、垂直分速度以及流场旋转分速度,对于形状较锋利的颗粒,初速度的水平分量将对材料表面进行切削、犁削。本文中假设为不够锐利的球形颗粒,颗粒在撞击过程中主要是推挤材料表面,使部分材料堆积在运动的前方,并且沟槽的两侧堆积有部分碎屑,水平速度变化曲线表明在4 μs 以后,颗粒开始接触工件表面,在冲击的过程中与工件表面发生能量交换,速度迅速下降,工件表面在颗粒的强烈冲击下发生了弹塑形变形,颗粒在10 μs时脱离被冲击表面,水平分速度趋于平稳。颗粒垂直分速度是造成材料表面应力应变加剧直至部分材料剥落的主要因素,图中竖直分速度的变化趋势较大,在整个碰撞过程中改变了速度方向,主要是因为碰撞表面有一定的倾斜度,颗粒碰撞后的运动方向主要以竖直方向为主。初速度的旋转分速度在撞击过程中无明显变化趋势,其作用主要是控制颗粒的冲击轨迹。
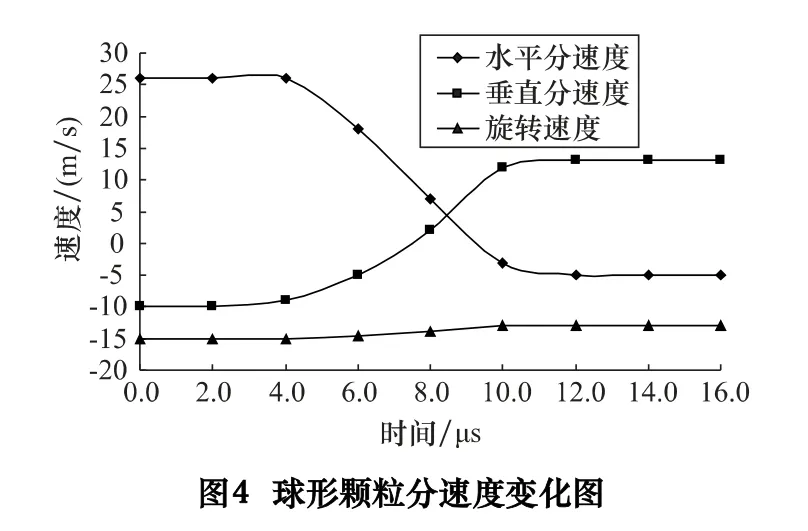
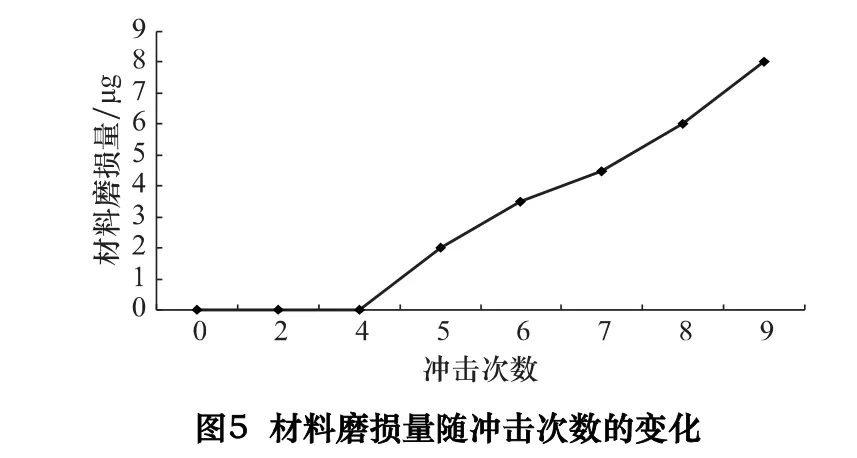
图5 为材料磨损量随颗粒冲击次数的变化图,颗粒在碰撞的初期不会发生材料的磨损,随着碰撞次数的增加材料磨损量也在逐渐增加。
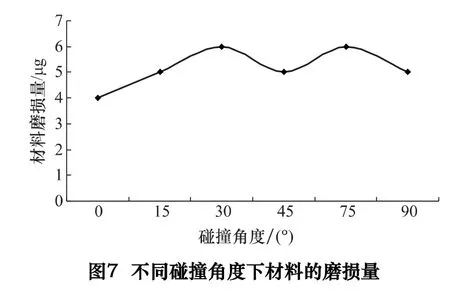
冲击角是颗粒冲击过程中影响材料磨损的重要参数。冲击角一般是指颗粒运动轨迹和工件表面之间的夹角。Finnie 理论认为颗粒以一定的倾斜角冲击时会使塑性材料表面产生更大的磨损,塑性材料破坏的最佳冲击角度在15°~30°之间,而脆性材料的最佳冲击较为90°。由于本文的撞击表面为一斜面,为研究颗粒的碰撞角度对材料磨损量的影响,本文定义冲击角为颗粒运动轨迹与水平面的夹角,设定颗粒的冲击速度为30 m/s,图6 为颗粒连续冲击8 次后的材料磨损情况。为进一步研究入射角对材料磨损量的影响,绘制材料磨损量随颗粒入射角的变化曲线,如图7 所示,从图中的曲线变化趋势可以看出:颗粒在水平和竖直方向冲击工件表面时材料磨损量较低,而在20°~35°以及60°~80°之间材料去除量较高,当颗粒的碰撞角度接近于零时,颗粒只有水平方向的分速度,材料的变形损伤层较薄,此时只有部分材料被切削。当冲击角为45°时材料去除量出现了低谷。主要是因为颗粒与斜面垂直碰撞,对于塑性材料,垂直撞击一般发生弹塑性变形,材料去除量比较少。而本文中的撞击对象为起伏型冲击表面,垂直撞击也会有部分材料发生去除。

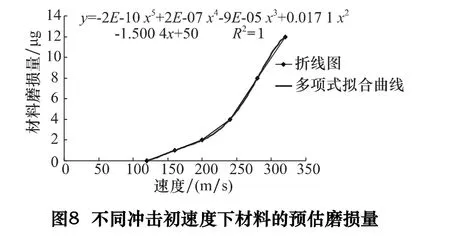
在磨粒的初次冲击下,不同的冲击初速度对材料磨损量的影响也不同,图8 为材料磨损量随冲击初速度的变化图,设定颗粒与工件表面的冲击角度为30°。由图可知当颗粒的初速度小于120 m/s 时,颗粒的初次冲击并未出现材料去除的现象,当颗粒的初速度介于120 m/s 到150 m/s 之间时,材料去除量极小,呈现出线性的关系,主要是因为撞击速度较低时,工件表面发生弹塑性变形但没有达到材料去除的极限值。随着冲击初速度的增大,材料磨损量也有所增加,而且后期增加的速度也逐渐在加快。为进一步描述材料磨损量与颗粒冲击初速度之间的函数关系,本文设材料磨损量W=F(ν),其中F(ν)为冲击初速度ν 的函数,定义F(ν)的表达式为
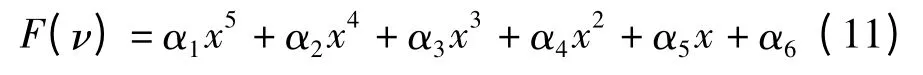
由图8 的拟合曲线可知:相关系数R2=1,曲线有近乎完美的拟合效果,拟合参数α1=-2 ×10-10,α2=2 × 10-7,α3=-9 × 10-5,α4=0.0171,α5=-1.5004,α6=50。
3 实验研究
德国学者的大量实验研究表明[15]:工件的表面质量、平行度等与研磨轨迹的均匀性密切相关,为了获得较好的表面质量和平面度,就需要对研磨轨迹进行研究。本文的仿真分析表明颗粒的旋转分速度的主要作用是控制颗粒的运动轨迹,所以通过改变颗粒旋转分速度的大小和方向,就能实现颗粒对工件表面全方位多角度的冲击,有利于实现研磨轨迹的错综复杂性,提高工件的加工效率和表面质量。本节将对以上理论进行实验研究。
3.1 搭建加工实验平台
螺旋式约束磨粒流加工装置如图9 所示。

3.2 加工试验
本实验选用污水泵参数为:流量为10 m3/h,扬程为15 m,磨粒流是将粒径为37 μm 的白刚玉与水和悬浮剂按照1:3:3 的体积比调配而成,加工工件选用铝合金空心缸筒,设定电动机的转速为1000 r/min。为研究颗粒的冲击轨迹对于工件表面加工质量的影响,设置对比实验,实验一使电动机正转加工40 h,实验二在加工20 h 后改变电动机的转向,对工件继续加工20 h。图10 为利用金相显微镜100 倍镜头观测工件加工后的表面形貌图:实验一,当电动机保持固定转向时,工件表面留有较多的冲击坑和冲击碎片,而且颗粒冲蚀划痕比较明显,呈现规律性,工件表面质量较差;实验二,当改变电动机转向时,工具表面纹理呈无序状,表面只有极少数冲击碎屑,工件表面的加工均匀度有了较大的提升,说明改变颗粒的冲击轨迹有利于实现错综复杂的加工纹理,工件表面的均匀性和加工效率都得到较大提升。

4 结语
(1)当颗粒的冲击速度较小时,冲击表面一般只发生弹塑性变形,随着冲击次数的增加,变形层增厚,材料的去除量逐渐增加,当颗粒的冲击速度较大时,在合适的冲击角度下可对工件表面材料进行切削去除。
(2)在冲击过程中,颗粒水平分速度直接参与材料的切削、耕犁。垂直分速度主要是控制材料变形层的厚度,旋转分速度能改变颗粒的冲击轨迹,实验结果表明改变旋转分速度的大小和方向能有效提高工件的加工效率和表面质量。
(3)在相同的冲击角度下,材料的磨损量随颗粒运动速度的增大而增加,材料磨损量随着颗粒的冲击角度的不同而不同,对于本文中的冲击模型,冲击角度太大或太小都不容易造成大量材料的磨损。
[1]Rhoades L J.Abrasive Flow Machining:a Case Study[J].Journal ofMaterials Processing Technology,1991,28(2):107 -116.
[2]计时鸣,唐波,谭大鹏,等.结构化表面软性磨粒流精密光整加工方法及其磨粒流动力学数值分析[J].机械工程学报,2010,46(15):178 -184.
[3]Ji S M,Xiao F Q,Tan D P.Analytical method for softness abrasive flow field based on discrete phase model[J].Science China:Technological Sciences,2010,53(10):2867 -2877.
[4]汤勇,周德明,杨钢,等.磨粒流光整加工性研究[J].华南理工大学学报,2001,29(9):17 -19.
[5]JiSM,Xiao F Q,Tan D P.Analytical method for soft -ness abrasive flow field based on discrete phase mode[J].Science China:Technological Sciences,2010,53(10):2867 -2877.
[6]Walker C I,Bodkin G C.Empirical wear relationships for centrifugal slurry pumps part1:side-liners[J].Wear,2000,242(1 -2):140 -146.
[7]Yabuki A,Matsumura M.Theoretical equation of the critical impact velocity in solid particles impacterosion[J].Wear,1999,233-235:476-483.
[8]唐学林,唐宏芬,吴玉林,等.水轮机转轮内固液两相紊流场数值模拟及磨蚀预估[J].工程热物理学报,2001,22(1):51 -54.
[9]姚启鹏.平面绕流泥沙磨损试验及水轮机磨损预估[J].水力发电学报,1997(3):69 -78.
[10]Finnie I.On the velocity dependence of the erosion of ductile metals by solid particles at low angles of incidence[J].Wear,1978(48):181 -190.
[11]BITTER J G.A study of erosion phenomena[J].Wear,1963(6):5 -21.
[12]Ahlert K R.Effects of paticle impingement angel and surface wetting on solid particle erosion on ANSI 1018 steel[M.S.Theses].USA:University of tulsa,1994.
[13]Finnie I.Some observation on the erosion of ductile material.wear,1972,19:81 -90.
[14]Johnson G R,Cook W H .A Constitutive Model and Data for Metals Subjected to Large Strains,High Strain Rat es and High Temperatures[C].Hague:Proceeding of 7th Internatio nal Symposium on Ballistics,1983,541 -547.
[15]Uhlmann E,Ardelt T.Influence of kinematics on the face grinding process on lapping machines[J].Annals of the CIRP,1999,48(1):281 -284.

