基于谱峭度和多元经验模式分解的机械故障诊断*
张 兵 于淑静 董绍江
(①连云港职业技术学院机电工程学院,江苏 连云港 222006;②重庆交通大学机电工程学院,重庆 400074)
机械故障诊断的实质就是机械设备运行状态的分类识别问题,故障特征的有效提取是实现准确故障诊断的关键[1-2]。实测振动信号往往受到噪声信号干扰,而早期故障信号中所含故障信息一般较弱,常常被淹没于宽频背景干扰噪声中。为有效提取机械故障特征,首先必须滤除信号背景噪声以强化故障特征相关信号分量。实测机械故障振动信号往往为低频谐波和多个调幅-调频信号分量的组合,具有明显的多载波多调制特性,这些低频谐波和调制分量中蕴含了丰富的机械状态信息,且其往往集中了信号主要能量成分[3-4]。显然,通过保留主要低频谐波和调制分量并滤除其余背景成分,可显著提高原信号信噪比。该策略的关键在于依据信号特点自适应构建带通滤波器组。近年来,谱峭度已被成功应用于背景干扰下信号冲击性特征的检测[5-6],其对非平稳信号分量的敏感性可为自适应带通滤波器组的设计提供参考。目前,经验模式分解(empirical mode decomposition,EMD)[7]因其对信号时间尺度的自适应局部化描述能力被广泛应用于机械故障诊断及特征提取中。然而标准的EMD 方法在实际应用中存在明显缺陷,首先是存在模式混叠问题,也即不同尺度成分出现在同一内蕴模式函数(intrinsic mode functions,IMF)中或者不同IMF 中存在相同尺度成分的冗余信息。其次,EMD 完全数据驱动及无法同时分解多元数据的特性使得两时间序列的分解结果无法实现同尺度特征的匹配,对于统计特征相同的两时间序列,其所得IMF 个数可能存在明显差别,同时EMD 分解的自适应性导致其尺度划分严重依赖于各信号本身而缺乏统一标准,从而很难保证两时间序列的同尺度IMF 特征能够对齐。此外,EMD 对时间序列的逐个分解方式缺乏对同一状态下数据内蕴信息的联合考虑。多元经验模式分解(MEMD)[8]将标准EMD 拓展到多元时间序列处理,它不仅具有与EMD 相同的自适应性及时频局部化分析能力,而且能有效解决EMD 存在的上述缺陷。目前,国内外学者对EMD 在机械故障诊断中的应用作了大量相关研究,但对MEMD 的相关报道极少。最近邻分类器(K -nearest neighbors classifier,KNNC)[9]是一种基于统计学的多分类方法,能直接利用训练样本特征和类标签信息来对测试样本进行分类决策,不仅时效性好,同时具有稳定的模式识别能力。
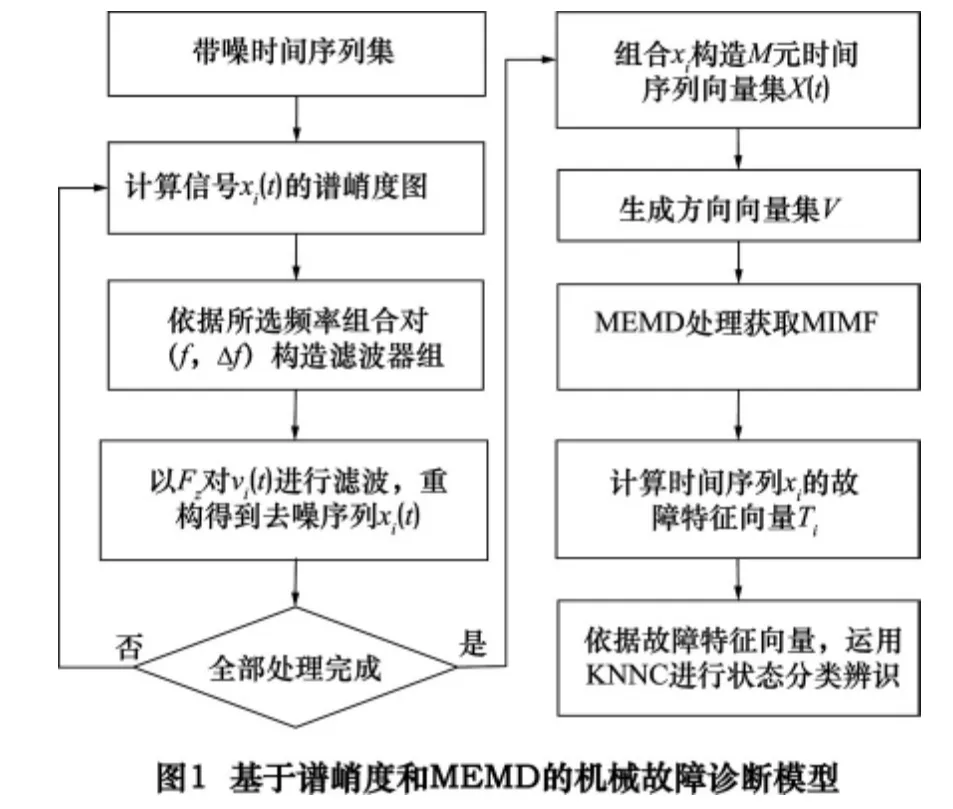
因此,基于谱峭度、MEMD 和KNNC 等技术,本文研究基于谱峭度和多元经验模式分解的机械故障诊断模型。首先借助于谱峭度方法对原始振动信号去噪以提高信噪比,然后利用MEMD 统一处理不同状态下振动数据,从具有统一尺度信息的各状态MIMF 分量中提取故障特征,最后依据特征向量利用KNNC 实现机械状态分类辨识。实验表明该模型可有效提取机械故障特征、具有很高的诊断精度和良好的抗噪性能。
1 基于谱峭度的信号去噪
为获取信号中主要低频谐波和调制分量并滤除其余背景成分,必须构建自适应带通滤波器组。谱峭度为理想滤波器组的输出在频率f 处计算得到的峭度值,由于谱峭度对非平稳信号分量十分敏感,且谱峭度估计与频率及频率分辨率的选择有很大关系,对任何非平稳过程,谱峭度是频率f 及分辨率Δf 的函数,因此,存在一个使谱峭度最大的最佳组合(f,Δf),该最佳组合(f,Δf)即标识了非平稳信号成分所在频谱位置,从而自适应滤波器的中心频率及其带宽可由(f,Δf)完全确定。基于短时傅里叶变换(STFT)定义的信号x(t)的谱峭度p(f)定义为[5]
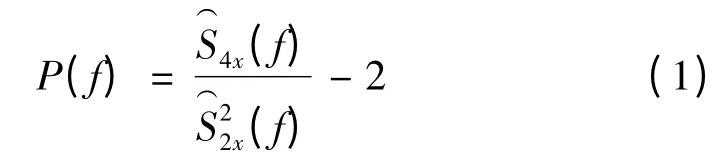
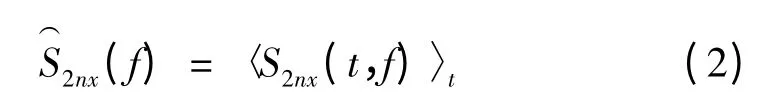
式中:S2nx(t,f)为信号x(t)在时间t 及频率f 位置的2n 阶瞬时矩,〈…〉t为时间平均算子。不同(f,Δf)组合下的谱峭度构成的谱图称为峭度图。为提取出多个频率成分,需要选择峭度图中最大的前Z 个峭度值对应的(f,Δf)作为滤波器参数并构造滤波器组Fz,利用Fz对信号x(t)逐一滤波处理,最后将所得Z 个滤波序列进行重构得到去噪信号序列。
2 基于MEMD 的特征提取
2.1 EMD
EMD 的目的是基于信号的局部特征时间尺度将复杂信号分解为有限个物理意义明确的固有模态函数(IMF)之和。IMF 必须满足两个条件[7]:(1)在整个数据段内,极值点的个数和过零点的个数必须相等或至多相差一;(2)在任何一点,有局部极大值点形成的上包络线与由局部极小值点形成的下包络线的均值为0。原始信号经EMD 处理后可表示为
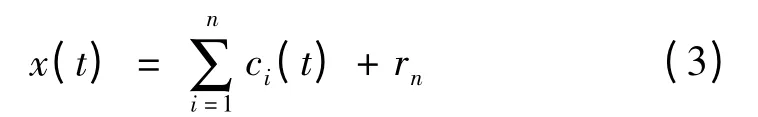
式中:c1(t),c2(t),…,cn(t)分别代表从高频到低频的调幅调频信号分量,rn为表示信号趋势的残余量。
2.2 MEMD
MEMD 旨在获取信号中与IMF 分量相似的多元内蕴模式函数(MIMF)。标准EMD 以信号上下包络的平均作为局部均值,并逐次筛分得到各IMF。与标准EMD 过程类似,MEMD 将N 元时间序列看成N 维向量,通过在N 维空间中沿不同映射方向对向量序列进行投影,然后计算各投影序列的包络,这些包络的平均值将作为多元时间序列的均值向量,其中投影方向向量选自球坐标系统。本文中,基于拟蒙特卡洛的低差异序列被用于生成单位球坐标系统中的方向向量[10]。以向量集X(t)={x1(t),x2(t),…,xM(t)}表示M 元时间序列,表示方向向量集X 中的第k 个向量,则MEMD 算法描述为[8]:
(1)生成合适的方向向量集V。
(2)沿每一个方向向量Vk(k=1,2,…,l)计算向量X(t)的投影Pk(t),其中l 为向量集V 中方向向量数目。
(3)寻找投影集{Pk(t)}中每个投影的极大值点,并记录对应时间刻度。
(6)提取向量序列D(t)=X(t)-C(t),如果D(t)满足MIMF 停止条件,则将D(t)作为一个MIMF分量,并对残余向量r(t)=X(t)-D(t)重复上述筛分过程,否者继续筛分D(t)至其满足MIMF 停止条件。
MEMD 中MIMF 停止条件类似于标准EMD 分解过程,但由于多元信号分解中极值点无法直接准确定义,因此停止条件并不要求极值点个数与过零点个数相等。MEMD 不仅保证了多元信号分解所得MIMF 个数相同,而且对于不同时间序列,代表相同尺度的MIMF 分量位于分解结果的同一位置。
2.3 特征提取
由于机械系统振动信号的频率结构与机械系统结构特征、运行状态密切相关,而MIMF 对应了系统从高频至低频段的不同频率成分,因此振动信号经MEMD分解后各尺度下的MIMF 的能量分布特征可用以反映机械运行状态。
设时间序列xi(t),xi(t)∈X 经MEMD 分解后第j个MIMF 分量为τi,j,则其对应的平均能量Ei,j可表示为
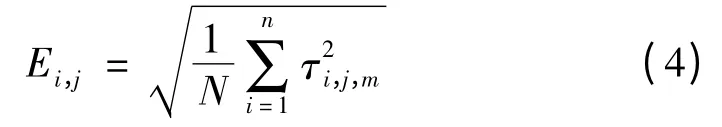
式中:τi,j,m表示τi,j中第m 个离散点的幅值。构造能量分布特征向量
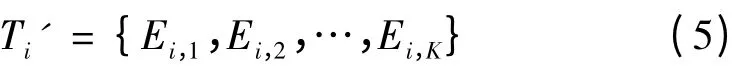
式中:K 为MEMD 所得MIMF 数目。最后,对特征向量Ti' 进行归一化处理,则时间序列xi(t)的故障特征向量Ti为:
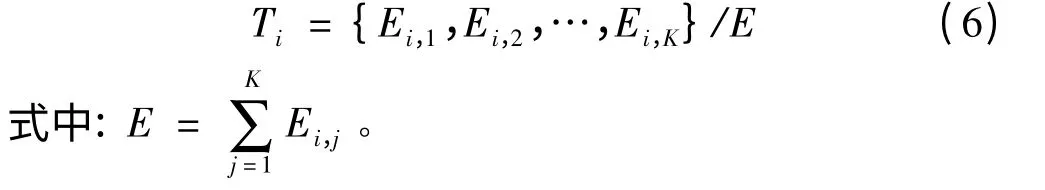
3 机械故障诊断模型
最近邻分类器(KNNC)是从训练样本集L 中搜索与未知样本d 最近的K 个邻域样本,通过判断K 个邻域样本与d 的相似性为邻域类加权,类权值之和最大的类别Ci即为d 的类别C。综合上述分析,所提故障诊断模型结构框图如图1 所示。
4 实例分析
齿轮箱是机械系统中极为重要且应用广泛的传动部件,对其运行状态进行辨识具有重要的现实意义。对采自某MFS-MG 机械故障综合模拟试验台的齿轮箱振动加速度信号进行分析,电动机用以驱动一谐波减速器,试验台主轴与谐波减速器输出端直连,被测齿轮箱与主轴通过皮带传递动力,电器控制装置和电磁制动器分别用以控制转速和加载力。电机转频为34.37 Hz,分别测取正常、缺齿、断齿及磨损四种不同状态下的齿轮箱振动信号各40 组(共160 组数据),信号采样频率为10 kHz,随机抽取四种状态下振动信号数据各20 组作为训练样本,各状态剩余20 组数据作为测试样本。使用每组数据前1024 点进行分析。
图2a 和图2c 分别为齿轮箱正常、断齿故障振动信号时域波形,显然原始振动信号中包含大量背景噪声,齿轮箱运转过程中的周期性冲击基本被淹没而无法辨识(受篇幅限制,本文仅以正常和断齿故障信号进行详细说明)。应用本研究中所述的基于谱峭度的去噪方法对该原信号进行处理(分解层数设置为5,滤波器个数Z=7)。图2b 和图2d 分别为图2a、图2c中信号去噪后时域波形,从中可看出明显的周期性冲击,而这些周期性冲击蕴含了丰富的设备运行状态信息。因此,所提基于谱峭度的去噪方法可有效提高信号信噪比,并强化信号中相关故障特征信息。
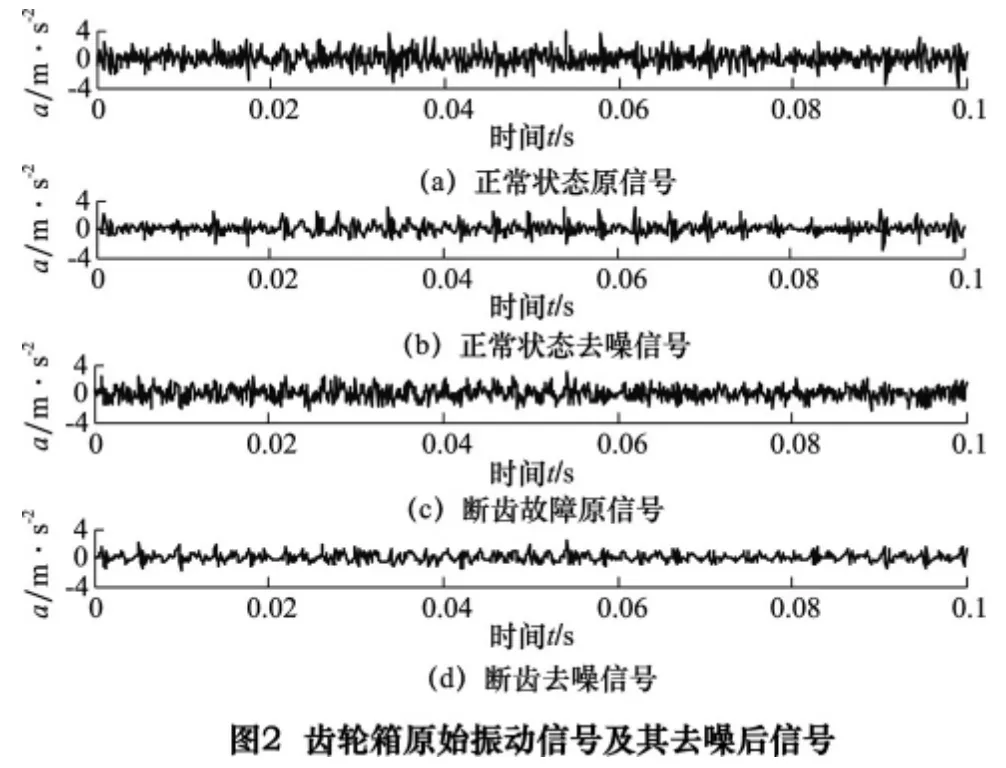
图3 和图4 分别给出了EMD 算法及MEMD 算法对图2 中去噪后信号的分解结果。从图3 可知,正常状态信号与断齿故障信号所得的IMF 分量个数不同(正常状态与断齿状态下有效IMF 个数分别为6 和8),而且对比图3a 和图3b 易知,两时间序列的同尺度特征无法对齐(如图3a 的IMF2 与图3b 中的IMF3、图3a 的IMF5 与图3b 中的IMF7 具有更为接近的尺度)。显然,若直接选取正常状态与断齿故障的前6 个IMF进行特征提取,则必然导致所提特征向量无法准确描述原信号真实能量分布特征。相比之下,图4 中所示MIMF 分解结果不仅保证了不同信号得到相同数量的MIMF,而且不同信号在同一分解层次上占据相似的尺度,且不同信号同尺度下MIMF 的幅值存在明显差异,因此,从MIMF 中所提能量分布特征能反映机械设备不同运行状态,而且为不同状态下特征向量的同尺度比较提供了可能。
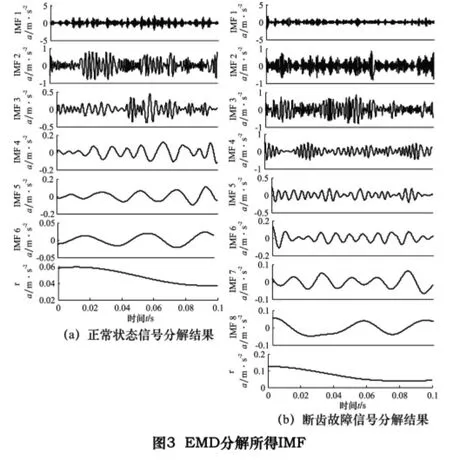
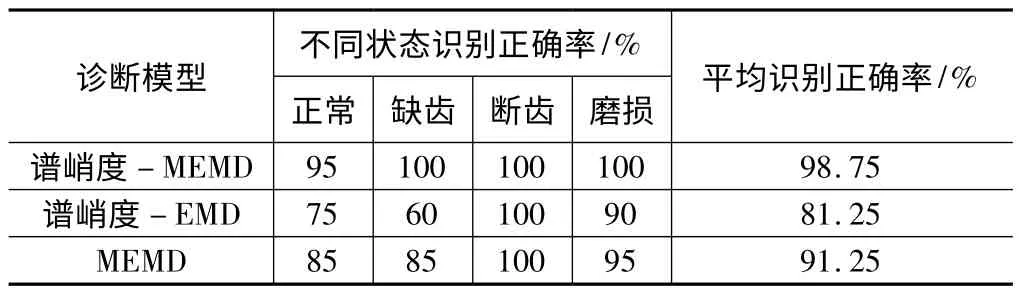
表1 不同诊断模型识别率对比
表1 为将各状态样本能量分布特征作为特征矢量输入KNNC 所得分类决策结果。为了评价所提故障诊断方法中各主要环节对决策结果的影响,实验对比了3 种故障诊断模型,分别记为谱峭度-MEMD,谱峭度-EMD 和MEMD。谱峭度-MEMD 为所提基于谱峭度和MEMD 的故障诊断模型;谱峭度-EMD 为基于谱峭度去噪后,从EMD 所得IMF 分量中提取能量分布特征;MEMD 为直接对原信号进行MEMD 分解并提取能量分布特征。由于不同信号EMD 所得IMF 个数不同,谱峭度-EMD 实验中仅前K' 个IMF 用以特征提取,其中K' 由最少有效IMF 数目决定。从表1知,3 种不同故障诊断模型均能较为准确的识别齿轮箱状态。对比分析易知,基于谱峭度的去噪方法降低了背景噪声对类别辨识的干扰,且MIMF 所得能量分布特征向量较IMF 所得特征向量更利于不同状态信号的同尺度比较,更适用于机械运行状态辨识。
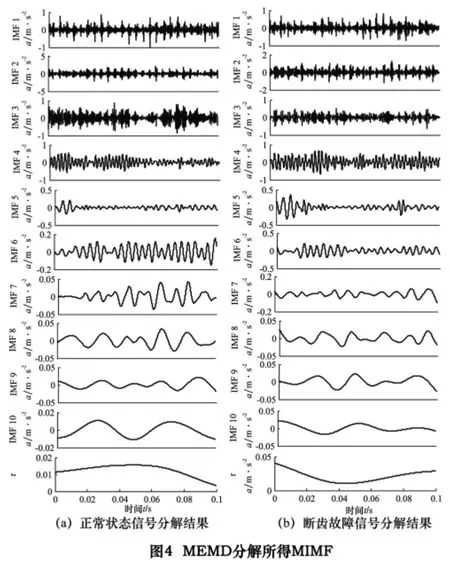
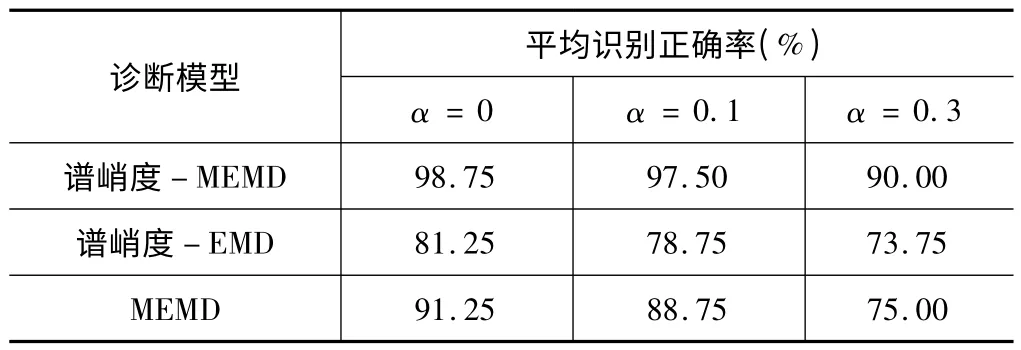
表2 不同诊断模型抗干扰性能对比
实际的机械故障诊断过程中,外界复杂环境干扰带来的背景噪声使得从振动信号提取故障特征更为困难。为检测基于谱峭度和多元经验模式分解的机械故障特征提取对复杂背景噪声下样本状态的辨识能力,在测试样本中人为加入随机噪声干扰,从而测试样本更改为
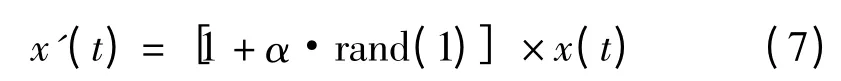
式中:x(t)为原始测试数据;rand(1)为(-1,1)间的随机数,α 为干扰系数。对干扰系数α=0.1,α=0.3时的测试样本应用不同故障诊断模型进行诊断,其诊断结果如表2 所示(为降低随机性的影响,α=0.1,α=0.3 分别运行10 次以其平均值作为结果),从表2可以看出,所提机械故障诊断模型不仅具有故障较高的诊断精度同时具有良好的抗噪性能。
5 结语
本文提出基于谱峭度和MEMD 的机械故障诊断模型。依据谱峭度对非平稳信号分量的敏感性特性自适应地设定带通滤波器组参数,运用构建的带通滤波器组对原信号进行滤波处理以提高原信号信噪比。多元经验模式分解对不同状态振动信号进行统一处理,保证了各信号MIMF 分量的同尺度匹配,提升了不同状态数据能量分布特征向量所含的类别信息。齿轮箱信号分析结果表明,基于谱峭度和MEMD 的机械故障诊断模型能有效辨识齿轮箱运行状态,且具有较高的诊断精度,为机械振动信号的特征提取和故障识别提供了参考。
[1]万鹏,王红军,徐小力.局部切空间排列和支持向量机的故障诊断模型[J].仪器仪表学报,2012,33(12):2789 -2795.
[2]Li Bing,Zhang Peiling,Liu Dongsheng,et al.Feature extraction for rolling element bearing fault diagnosis utilizing generalized S transformand two-dimensional non-negative matrix factorization[J].Journal of Sound and Vibration,2011,330(10):2388 -2399.
[3]张焱,汤宝平,邓蕾.基于小波脊线的多分量信号瞬时参数估计及应用[J].机械工程学报,2014,50(5):17 -24.
[4]张永祥,苏永生,喻祖如,等.基于小波降噪的共振解调技术在齿轮箱故障诊断中的应用[J].机械设计与制造,2006,10:149 -151.
[5]Antoni J.The spectral kurtosis:a useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing,2006,20(2):282 -307.
[6]Xiong Xin,Yang Shixi,Gan Chunbiao,A new procedure for extracting fault feature of multi-frequency signal from rotating machinery[J].Mechanical Systems and Signal Processing,2012,32:306–319.
[7]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C].Proceedings of the Royal Society of London.Series A:Mathematical,Physical and Engineering Sciences,1998:454,903-995.
[8]Zhao Xiaomin,Patel T H,Zuo M J.Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J].Mechanical Systems and Signal Processing,2012,27:712 -728.
[9]宋涛,汤宝平,李锋.基于流形学习和K-最近邻分类器的旋转机械故障诊断方法[J].振动与冲击,2013,32(5):149 -153.
[10]Rehman N,Mandic D P.Multivariate empirical mode decomposition[C]Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Science,2010,466:1291–1302.

