空腔位置及结构对脉冲压力振荡的影响

苏万兴，王宁飞，李要建，陈升泽，李军伟，孙兵兵

(1.中国运载火箭技术研究院研究发展中心，北京 100076；2.北京理工大学 宇航学院，北京 100081)



空腔位置及结构对脉冲压力振荡的影响

苏万兴1,2，王宁飞2，李要建1，陈升泽1，李军伟2，孙兵兵2

(1.中国运载火箭技术研究院研究发展中心，北京 100076；2.北京理工大学 宇航学院，北京 100081)

为了获得不同空腔位置及结构对脉冲压力振荡特性的影响规律，利用Fluent软件并结合UDF(用户自定义函数)，对4种不同空腔模型的发动机开展了数值计算，得到了燃烧室内的流场结构与脉冲压力振荡特性，为发动机装药结构设计及不稳定燃烧抑制提供了理论指导。结果表明，头部空腔能有效衰减脉冲波动压力，有利于提高发动机的工作稳定性；中间位置空腔内容易产生旋涡脱落现象，继而诱发涡声耦合压力振荡，扩张式中间空腔内压力振荡比收敛式中间空腔内的压力振荡严重；末端空腔不仅削弱了喷管阻尼，而且在脉冲条件下易激发旋涡脱落，不利于发动机工作稳定性，在工程设计中，应慎重考虑翼面后置装药结构。

固体火箭发动机；空腔；脉冲压力振荡；不稳定燃烧

0 引言

不稳定燃烧现象是固体火箭发动机研制过程中经常遇到的棘手问题之一，其基本特征是燃烧室压强作周期或近似周期性的变化[1]。众多因素可诱发不稳定燃烧现象，如推进剂压力耦合响应、涡声耦合、分布燃烧等[2-5]。针对不稳定燃烧，国内外开展大量的试验、理论与数值研究工作[2,6-13]。以法国国家航天航空研究中心(ONERA)为首的欧洲国家，针对Ariane5固体助推器P230中出现的压力及推力振荡问题，开展了ASSM项目及POP计划[6,12]，深入研究了涡声耦合对压力振荡的诱发机理。为了解决航天飞机助推发动机 RSRM、Titan IV 助推发动机SRMU中出现的不稳定燃烧问题，美国自1995年开始进行了多学科大学创新研究计划(MURI)[11]，对发动机燃烧室内的基元化学反应、金属燃烧和气体动力学进行了模型和试验研究，全面认识了火箭发动机中推进剂不稳定燃烧的耦合方式以及影响不稳定燃烧发展的因素。美国海军空战中心(Naval Air Warfare Center) 的Blomshield[13]针对多种复合推进剂，利用T型燃烧器进行了大量的试验研究，总结了配方及工作条件对压力耦合响应函数的影响规律。国内北京理工大学王宁飞教授与西北工业大学刘佩进教授在不稳定燃烧领域开展了大量研究工作，在涡声耦合[14-15]、推进剂压力耦合响应[16-17]、非线性不稳定燃烧[18]、不稳定燃烧预示及抑制[19]等领域，取得了一定的进展。

近年来，随着导弹武器技术的发展，大推力、远射程等军事需求的不断提高，众多战术导弹采用了大长径比、翼柱装药结构的固体火箭发动机[20]，此类结构发动机在工作过程中，随着翼面的消失在燃烧室内形成空腔结构；另外，对于分段固体火箭发动机，段与段的连接处会存在狭缝结构[21-23]。不同的空腔位置对发动机工作稳定性的影响不尽相同。Blomshield[2]研究表明，主燃面位于燃烧室末端容易引发压力振荡现象。Gallier等[24]针对P230 缩比试验发动机进行了试验及数值研究。结果表明，末端空腔易于产生不稳定燃烧现象。张峤[25]通过数值计算表明，头部空腔对燃烧室内的压力振荡有一定的抑振作用。然而，在Prevost等[12]对LP9发动机的试验研究中发现，在发动机头部增加空腔，压强振幅反而有增大的趋势，但并未对该现象做出解释。此外，对于中间位置空腔对发动机工作稳定性的影响也缺乏公开报道。因此，在固体火箭发动机装药设计中，空腔结构对发动机工作稳定性的影响还存在一定的争议与不足之处。基于此，本文针对不同空腔位置及不同空腔结构展开数值计算研究，系统探讨空腔对燃烧室内脉冲压力振荡的响应特性的影响规律，为发动机装药结构设计与不稳定燃烧抑制提供理论指导。

1 数值模型与边界条件

1.1 数值计算模型及方法

本文采用了简单的管型发动机，并将其简化为二维轴对称模型，基本模型如图1所示。燃烧室空腔长度为1 m，半径0.1 m，喷喉半径30 mm，喷管收敛段为简单的锥型型面，收敛半角为45°。为了研究空腔位置及结构对流场及脉冲压力振荡特性的影响，在该模型的基础上，分别在发动机的头部、中间位置及末端引入同样大小的空腔。空腔位于中间位置的情况下，分别定义了收敛式和扩张式2种类型的空腔结构，具体结构见下文。需说明一点，在本文定义的扩张式空腔中，扩张角满足产生转角旋涡脱落的条件。为了便于记录燃烧室内的压力变化，在头部设置了虚拟压力监测点，同样如图1所示。

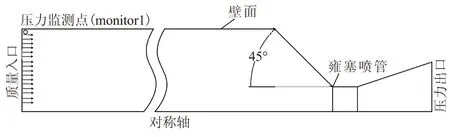
图1 数值计算基本模型Fig.1 Basic numerical model

本研究中，主要关注燃烧室内受到脉冲触发后的压力振荡特性，而不去关心流场细微的流动特性，因而采用了两方程湍流模型。选用了标准k-ε湍流模型，对雷诺平均Navier-Stokes方程进行封闭。在数值计算中，首先对流场开展了稳态迭代，当迭代至5 000步左右流场较好的收敛以后，继而开启非稳态流场计算。时间项采用二阶隐式格式，计算步长为5×10-5s，CFL(Courant-Friedrich-Lewy)数设置为1。在非稳态计算过程中，发动机头部以固定的质量流率向燃烧室内注入气体以维持平衡压力，当监测点压力不再波动时，通过UDF(User Defined Functions)瞬时增大质量流率用以模拟脉冲波，具体方法详见文献[19]。通过分析不同空腔下的流动特性与脉冲压力振荡特性及阻尼特性，来综合反映不同空腔结构对发动机稳定性的影响。

1.2 边界条件

边界条件同样如图1所示，采用了轴向加质的方式，发动机头部为质量入口，将气体工质视为理想气体处理。计算中，不考虑推进剂燃烧化学反应过程，介质温度为3 000 K。出口采用了压力出口条件，在壁面边界上选取无滑移边界条件。在不同的计算模型中，基本边界条件均保持一致。

2 流场特性

2.1 稳态流场特性

首先，针对不同空腔结构开展了稳态流场计算，所得速度流线图如图2所示。

由图2可见，当在燃烧室内引入空腔后，空腔内均会产生明显的回流泡，表明空腔内气流产生了分离，严重时将会产生旋涡脱落现象。空腔位于不同的位置，气体回流现象将对燃烧室内的压力振荡特性产生不同的影响。从声学角度讲，头部空腔和末端空腔均处于声压波腹，是对称位置。然而，末端气流速度大，流场特性复杂；另外，末端空腔使得通气面积增大，导致喉通比下降，这将对喷管阻尼特性产生很大的影响。中间空腔位于一阶声振型速度波腹的位置，此处速度振幅达到最大值，微弱的速度扰动极易被放大，当旋涡脱落源位于速度波腹位置时，容易激发较严重的涡声耦合压力振荡现象[26]。

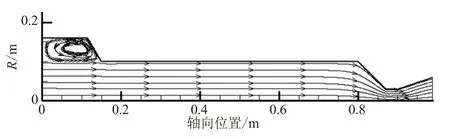
(a) 头部空腔

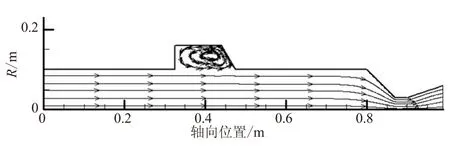
(b) 收敛式中间空腔

(c) 扩张式中间空腔

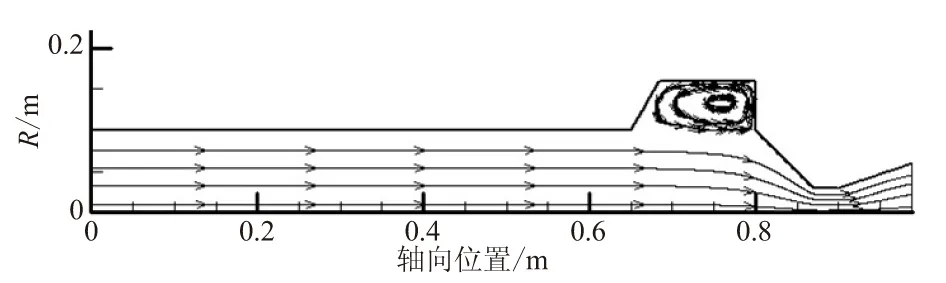
(d) 末端空腔

发动机头端至末端的流动特性不尽相同，在发动机头部，发动机内的流动基本为层流状态；在发动机末端，气流速度增大，发动机内的流动由层流状态逐渐过渡至湍流状态。因此，在发动机不同位置空腔产生的旋涡脱落强度也不尽相同，旋涡脱落引起的压力振荡也有所不同。此外，空腔结构不同，对旋涡的形成、碰撞及反馈也会有一定的影响。下文将详细探讨非稳态条件下，不同空腔位置及结构下的旋涡脱落现象及压力振荡特性。

2.2 非稳态流场特性

空腔内气流产生流动分离现象可直观地通过旋涡脱落来表征，反映旋涡脱落强度的参数为涡量。本节中，主要以涡量图来描述不同位置及不同形状空腔内的非稳态流场特性。非稳态计算过程中，在0～0.1 s之间，发动机头部以固定的质量流率向燃烧室注入气体，在0.1 s时刻，质量流率突然增大，在燃烧室内激发压力振荡，随后质量流率恢复至初始值，脉冲产生的压力振荡逐渐衰减，通过分析脉冲压力振荡幅值来评估空腔对发动机工作稳定性的影响。下文分析中，0～0.1 s为无脉冲流动，0.1 s以后为脉冲后流动。空腔位于发动机头部时，由于空腔位于气流入口附近，该处气流速度较低，尽管空腔内产生了气流分离，存在回流泡，但气流强度不足以形成旋涡脱落现象。

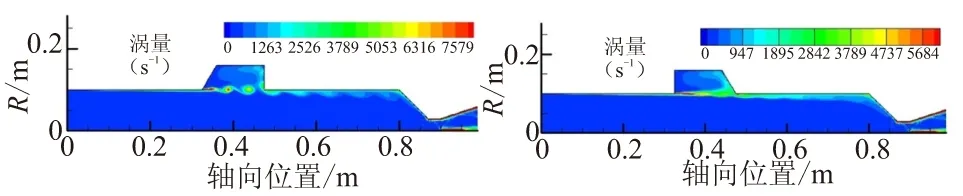
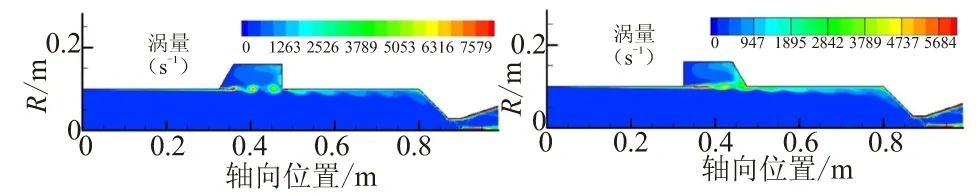
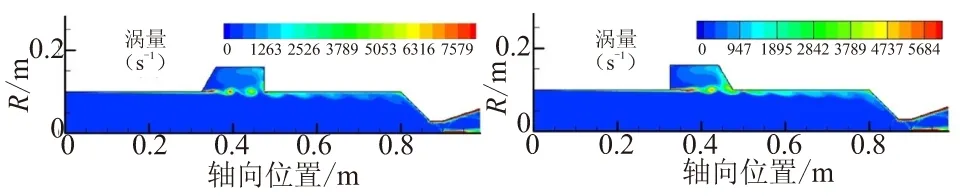
空腔位于燃烧室中间位置时，空腔内产生了较明显的旋涡脱落现象。时间脉冲前(0～0.1 s)空腔内的旋涡运动轨迹如图3所示。图3中，左端为扩张式中间空腔，右端为收敛式中间空腔，图3(a)、(b)、(c)、(d)之间的时间间隔为0.01 s。

(a) t=0.05 s

(b) t=0.06 s

(c) t=0.07 s

(d) t=0.08 s

从图3左端的扩张式中间空腔内的旋涡运动轨迹可看出，气流流经空腔前缘倾角时产生了流动分离，继而形成了旋涡脱落现象，脱落的旋涡随主流向下运动，至空腔后缘处碰撞破碎，部分沿着燃烧室壁面向下游运动，剩余部分沿空腔后缘向上游运动，形成了图2(c)所示的回流泡现象。在图3右端的收敛式空腔内，直至t=0.06 s时，才形成旋涡脱落现象。与扩张式空腔内旋涡运动轨迹比较，收敛式空腔内旋涡核心位于空腔中间位置，而扩张式空腔内旋涡核心位于空腔前缘附近。另外，对比两种空腔内旋涡核心处的涡量可发现，扩张式空腔内旋涡核心涡量可达8 000 s-1，而收敛式空腔内的旋涡核心涡量最大仅为6 000 s-1，表明扩张式中间空腔内的旋涡强度要强于收敛式空腔内的旋涡强度。这是由于收敛式空腔前缘倾角有利于气流分离，容易形成旋涡脱落，而空腔后缘为直角，不仅不利于旋涡的衰减与扩散，而且直角能够加强声能反射。从发动机稳定性角度分析，扩张式中间空腔内的压力振荡程度将会高于收敛式空腔内的压力振荡，不利于发动机的稳定性。

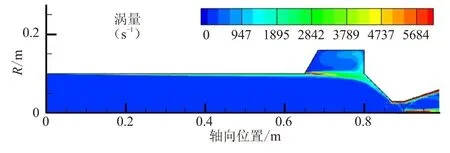
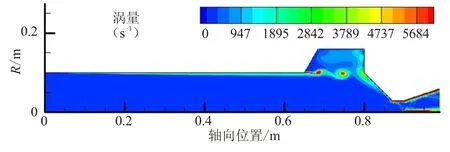
当空腔置于燃烧室末端时，在施加脉冲之前(0.1 s之前)，末端空腔内没有形成旋涡脱落现象，如图4(a)所示。可看出，空腔开口位置处存在明显的气流剪切层，该剪切层从空腔前缘延伸至空腔后缘和喷管收敛段处。剪切层在空腔后缘处碰撞产生气流折转，在空腔内形成了图2(d)所示的回流泡现象。由于末端空腔与喷管连接，收敛段处气流加速，剪切层气流强度容易被加速的主流气体所耗散，不易于形成稳定的旋涡脱落现象。当燃烧室内施加脉冲后(0.1 s后)，入口处气体质量流率瞬时增大，导致剪切层气流强度增大，使其能够克服主流区域的阻力，形成了旋涡脱落现象，如图4(b)所示，旋涡核心处涡量可达6 000 s-1左右。当脉冲结束后，质量流率回复至初始水平，剪切层强度变弱，空腔前缘倾角处不再产生新的旋涡。脉冲后产生的旋涡随主流往下游运动，运动的过程中，旋涡强度逐渐被衰减，图4(c)中，旋涡核心处涡量仅为4 500 s-1左右。旋涡运动至喷管收敛段处碰撞破碎，直至消失。最后，燃烧室内的流场分布与脉冲前保持一致，如图4(d)所示。

(a) t=0.1 s

(b) t=0.12 s

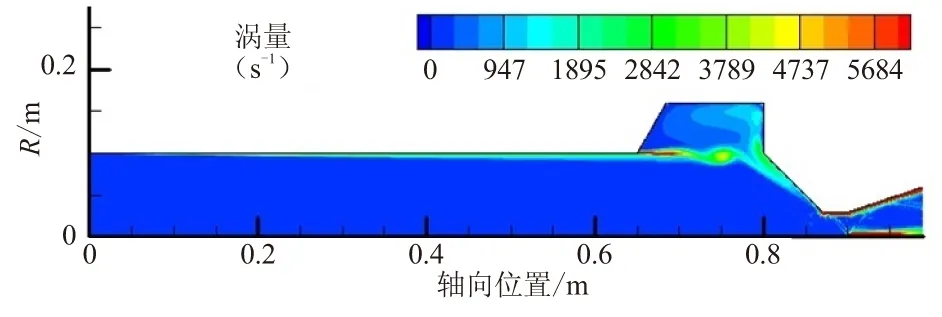
(c) t=0.14 s

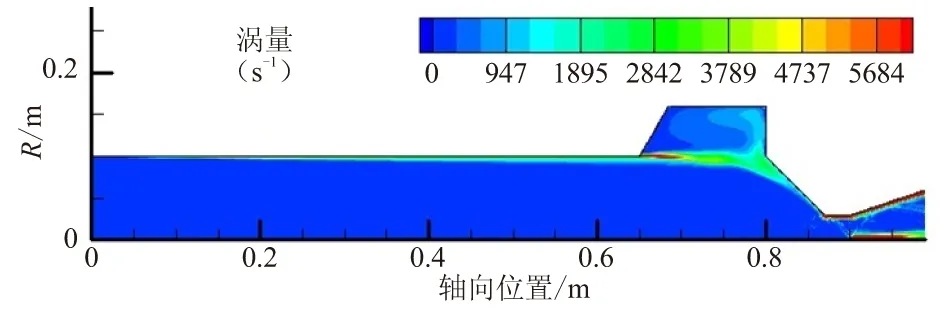
(d) t=0.16 s

综上分析，不同空腔位置与空腔形状对燃烧室内的流场特性影响各不一样，因而对脉冲压力振荡特性也会有不同影响。下一章将集中讨论对压力振荡特性的影响，后续分析中，以头部监测点数据为例。

3 脉冲压力振荡特性

本章将分别计算含有不同空腔位置、不同空腔结构发动机内的脉冲压力振荡特性，并与不含空腔发动机内的脉冲压力振荡特性进行对比分析，总结空腔对发动机工作稳定性的影响。

3.1 头部空腔脉冲压力振荡特性

对含有头部空腔和不含头部空腔的模型进行数值计算。2种模型采用了同样的脉冲强度，脉冲后波动压力衰减过程见图5。图5中，实线代表含有头部空腔模型，虚线代表不含空腔模型。由图5可明显看出，引入头部空腔后，在燃烧室受到同等脉冲的激励的情况下，含头部空腔发动机内的脉冲波动压力幅值明显低于不含空腔的发动机，这就意味着头部空腔起到了一定的抑制压力振荡的作用。如上一章所述，头部空腔内存在回流泡现象，但没有产生旋涡脱落现象。因此，当燃烧室受到脉冲激励后，部分声能将被空腔内的回流现象所耗散，提高了发动机的整体稳定性。

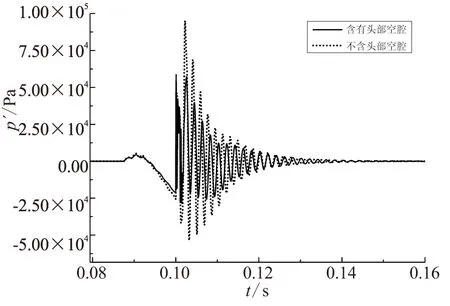
图5 含/不含头部空腔下脉冲压力振荡衰减过程Fig.5 Pulsed pressure oscillations (with/without head cavity)

Prevost等[12]对Ariane助推器的缩比发动机(LP9-No.15)点火试验中发现，在发动机头部增加空腔，压力振幅反而有增大的趋势，但未对该现象进一步解释。作者认为，LP9-No.15发动机的长径比较大，容易诱发表面旋涡脱落，LP9-No.15发动机增加的头部空腔使得发动机总长度进一步增大，使其更易出现表面旋涡脱落现象，因此加入头部空腔后，压力振幅增大是由于表面旋涡脱落强度增大所致。在本研究中，发动机长径比较小，不存在表面旋涡脱落现象；另外，引入空腔也未改变发动机的长度。结果表明，引入头部空腔后，对脉冲压力振荡具有显著的抑振作用，抑振原理与LP9-No.15内的空腔作用不尽相同，对于长径比不大的发动机而言，头部空腔对抑制不稳定燃烧的作用是可观的。

3.2 末端空腔脉冲压力振荡特性

对含有末端空腔和不含空腔模型的计算结果进行对比分析，结果如图6所示。可看出，引入末端空腔后，在受到同等脉冲强度的激励后，含有末端空腔的发动机压力振荡幅值明显高于不含空腔发动机；此外，含有末端空腔发动机内的压力衰减速率要低于不含空腔的发动机。由于发动机末端气流处于湍流状态，此处引入空腔后容易在空腔开口处形成气流剪切层，该剪切层与喷管碰撞将会进一步增强压力振荡。另外，当剪切层强度增大时，还易形成旋涡脱落现象，进而引起涡声耦合压力振荡。在末端引入空腔后，还会造成发动机喉通比J减小，进而导致喷管阻尼下降。因此，从涡声耦合增益及喷管阻尼角度而言，末端空腔均不利于发动机工作稳定性。

对于翼面后置的固体火箭发动机而言，工作至末期，形成末端空腔难以避免，为了尽可能减小末端空腔带来的压力振荡，要尽可能合理设计翼面后置的装药结构，在工作末期时，后翼面燃尽后形成的突扩角尽量避免出现在二阶声速波腹位置[26]，如果恰好在速度波腹位置，旋涡脱落强度将会进一步被激发，继而造成严重的压力振荡现象。

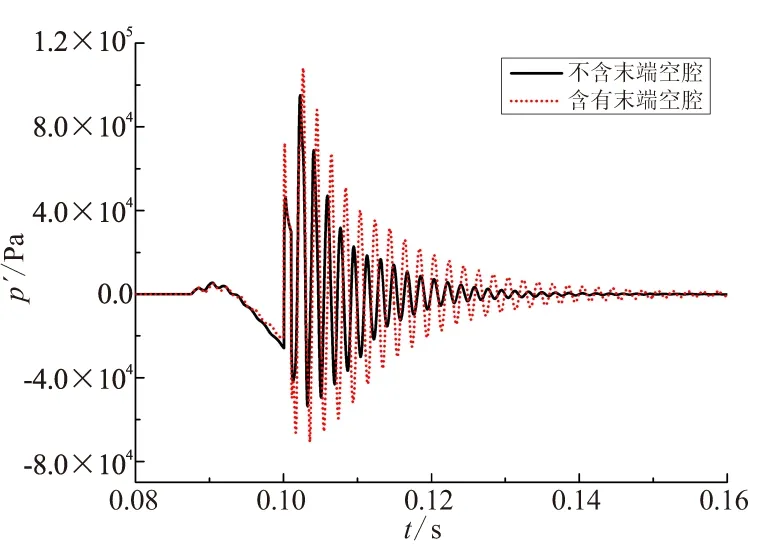
图6 含/不含末端空腔下脉冲压力振荡衰减过程Fig.6 Pulsed pressure oscillations (with/without end cavity)

3.3 中间空腔脉冲压力振荡特性

对含有扩张式中间空腔和不含空腔发动机的计算结果进行对比分析，结果如图7所示。在施加脉冲激励之前(0.1 s之前)，不含空腔的发动机内无压力振荡现象，发动呈稳定的工作状态；然而，在含有扩张式中间空腔的发动机内逐步产生了压力振荡现象，在0.05 s左右形成了稳定的周期性压力振荡，即所谓的极限振幅现象。这是由于在脉冲激励之前，不含空腔的发动机内不存在周期性扰动，而在扩张式中间空腔内存在周期性旋涡脱落现象。在图3(a)中，稳定的周期性旋涡脱落现象出现在t'=0.05 s左右，与图7内形成极限振幅压力振荡的时间对应，表明扩张式中间空腔内的压力振荡是由旋涡脱落引起的。当脉冲激励结束以后，不含空腔发动机内的压力振荡逐渐衰减，最终压力振荡消失。然而，在含有扩张式中间空腔的发动机内，压力振荡衰减至一定程度后，重新以极限振幅形式振荡。这是由于脉冲激励结束后，扩张式中间空腔内依然存在稳定的旋涡脱落现象。因此，极限振幅压力振荡现象始终存在。上述分析表明，收敛式中间空腔不利于发动机工作稳定性。

另外，对收敛式与扩张式中间空腔下的自激压力振荡进行了研究，2种空腔结构下的脉冲压力振荡衰减过程如图8所示。

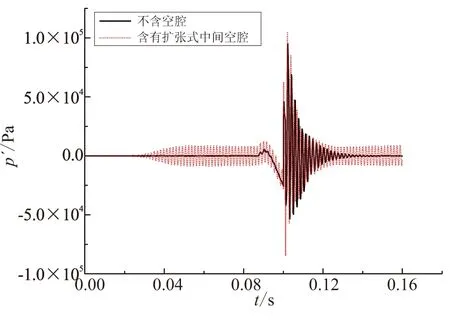
图7 含/不含中间空腔下脉冲压力振荡衰减过程Fig.7 Pulsed pressure oscillations (with/without convergent middle cavity)

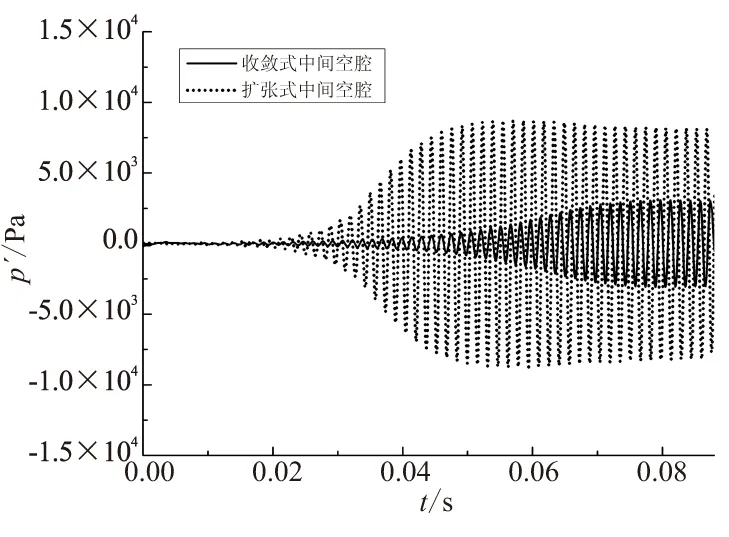
图8 不同中间空腔下脉冲压力振荡衰减过程Fig.8 Pulsed pressure oscillations in different middle cavities

可看出，无论是扩张式中间空腔，还是收敛式中间空腔，空腔内易产生周期性的旋涡脱落现象，因此会激发压力振荡。由非稳态流场特性分析可知，扩张式中间空腔内的旋涡核心涡量强度可达8 000 s-1，而收敛式空腔内旋涡核心涡量强度为6 000 s-1。因此，含扩张式中间空腔发动机内的自激励压力振荡幅值要明显高于收敛式中间空腔发动机内的振幅。此外，对比图3可知，扩张式中间空腔内，在t=0.05 s时，形成了稳定的旋涡脱落现象；而收敛式空腔内，在t=0.07 s时，形成了稳定的旋涡脱落现象。从图8同样可明显看出，该时间滞后，表明扩张式中间空腔更易产生旋涡脱落。

综上分析表明，头部空腔对脉冲压力振荡有一定的衰减作用，有利于提高发动机工作稳定性；扩张式和收敛式中间空腔内易产生周期性旋涡脱落现象，进而导致涡声耦合压力振荡，压力振荡呈极限振幅状态，均不利于发动机工作稳定性，而且扩张式内中间空腔内的极限压力振幅显著高于收敛式中间空腔内的压力振幅；末端气流处于湍流状态，此处引入空腔后，容易在空腔开口处形成气流剪切层，该剪切层与喷管碰撞将会进一步增强压力振荡；另外，施加脉冲能够加强气流剪切层强度，还容易形成旋涡脱落现象，进而导致脉冲压力振荡幅值进一步增大。因此，末端空腔也不利于发动机的稳定性。

在工程设计中，应尽量避免在发动机中间位置处形成空腔、台阶等结构。同时，也要尽可能避免在发动机末端形成空腔结构。如果翼面后置结构无法避免，需合理设计翼面装药段与圆柱装药段的交接位置，在工作末期时，后翼面燃尽后形成的突扩角避免出现在二阶声速波腹位置，从而尽可能减小旋涡脱落诱发的压力振幅。

4 结论

(1)燃烧室内不同空腔位置对发动机稳定性各不相同，头部空腔能够有效地衰减脉冲波动压力，有利于提高发动机的工作稳定性。

(2)中间位置空腔内易产生旋涡脱落现象，继而诱发涡声耦合压力振荡，扩张式中间空腔内压力振荡比收敛式中间空腔内的压力振荡严重。

(3)末端空腔一方面引起转角旋涡脱落，另一方面减小了喉通比J，导致喷管阻尼急剧减小，不利于发动机工作稳定性，在工程设计中，应慎重考虑翼面后置装药结构。

[1] 孙维申. 固体火箭发动机不稳定燃烧[M]. 北京: 北京工业学院出版社, 1987.

[2] Blomshield F S. Lessons learned in solid rocket combustion instability[R]. AIAA 2007-5803.

[3] 王宁飞, 张峤, 李军伟, 等. 固体火箭发动机不稳定燃烧研究进展[J]. 航空动力学报, 2011, 26(6): 1405-1414.

[4] 刘佩进, 金秉宁, 李强. 战术导弹固体发动机燃烧不稳定研究概述[J]. 固体火箭技术, 2012, 35(4): 446-449.

[5] 王宁飞, 苏万兴, 李军伟, 等. 固体火箭发动机中铝粉燃烧研究概述[J]. 固体火箭技术, 2011, 34(1): 61-66.

[6] Fabignon Y, Dupays J. Instability and pressure oscillations in solid rocket motors[J]. Aerospace Science and Technology, 2003, 7(3): 191-200.

[7] Gallier S, Godfroy F. Aluminum combustion driven instabilities in solid rocket motors[J]. Journal of Propulsion and Power, 2009, 25(2): 509-521.

[8] Sabnis J S. Numerical simulation of distributed combustion in solid rocket motors with metalized propellant[J]. Journal of Propulsion and Power, 2003, 19(1): 48-55.

[9] Golafshani M, Farshchi M, Ghassemi H. Effects of grain geometry on pulse-triggered combustion instability in rocket motors[J]. Journal of Propulsion and Power, 2002, 18(1): 123-130.

[10] Javed A, Chakraborty D. Damping coefficient prediction of solid rocket motor nozzle using computational fluid dynamics[J]. Journal of Propulsion and Power, 2014, 30(1): 19-23.

[11] Blomshield F S. Summary of multi-disciplinary university research initiative in solid propellant combustion instability[R]. AIAA 2000-3172.

[12] Prevost M, Godon J C, Innegraeve O. Thrust oscillations in reduced scale solid rocket motors, part I: experimental investigations[R]. AIAA 2005-4003.

[13] Blomshield F S. Pressure-coupled response of solid propellants[J]. International Journal of Energetic Materials and Chemical Propulsion, 2011, 10(2): 85-105.

[14] 张峤, 李军伟, 王伟臣, 等. 固体火箭发动机涡声耦合特性数值研究[J]. 推进技术, 2011, 32(3): 348-354.

[15] 陈晓龙, 何国强, 刘佩进, 等. 潜入式喷管对燃烧室中压力振荡的影响[J]. 固体火箭技术, 2010, 33(3): 252-255.

[16] 刘佩进, 齐宗满, 金秉宁, 等. 两种含铝复合推进剂压强耦合响应的实验对比[J]. 固体火箭技术, 2013, 36(1): 83-88.

[17] Su Wan-xing, Wang Ning-fei, Li Jun-wei, et al. Improved method of measuring pressure coupled response for composite solid propellants[J]. Journal of Sound and Vibration, 2014, 333(8): 2226-2240.

[18] 刘佩进, 魏少娟, 杨尚荣. 固体火箭发动机非线性燃烧不稳定分析方法[J]. 固体火箭技术, 2013, 36(3): 302-309.

[19] 苏万兴. 大长径比固体火箭发动机不稳定燃烧预示及抑制方法研究[D]. 北京：北京理工大学, 2015.

[20] 胡大宁, 何国强, 刘佩进, 等. 翼柱型药柱固体火箭发动机不稳定燃烧研究[J]. 固体火箭技术, 2010, 33(5): 502-506.

[21] 王健儒, 何国强, 李强, 等. 分段式固体火箭发动机内部流动不稳定性数值分析[J]. 推进技术, 2013, 34(1): 93-98.

[22] 刘佩进, 杨尚荣. 分段固体火箭发动机中声涡耦合现象的实验研究现状[J]. 固体火箭技术, 2013, 35(6): 726-731.

[23] 王建儒, 何国强, 许团委, 等. 燃烧室对接狭缝设计参数对压强振荡的影响研究[J]. 固体火箭技术, 2012, 35(4): 474-478.

[24] Gallier S, Prevost M, Hijlkema J. Effects of cavity on thrust oscillations in subscale solid rocket motors[R]. AIAA 2009-5253.

[25] 张峤, 李军伟, 苏万兴, 等. 头部空腔对固体火箭发动机压强振荡抑制作用的数值研究[J]. 固体火箭技术, 2012, 35(1): 34-41.

[26] 苏万兴, 李军伟, 张峤, 等. 涡脱位置及温度对涡声效应压力振荡影响研究[J]. 推进技术, 2013, 34(2): 248-253.

(编辑：崔贤彬)

《硼的点火和燃烧》

作 者：周俊虎、刘建忠、张彦威、汪 洋

书 号：978-7-03-040293-6

出版日期：2015年9月

开 本：16开

字 数：416000

定 价：158.00元

内容简介：硼的点火和燃烧相关研究是固体推进技术的关键科学问题。本书系统地介绍了硼颗粒及含硼燃料的物理化学特性、点火燃烧特性及其促进方法，点火和燃烧理论模型、微尺度下点火燃烧特性。涉及多种不同的实验技术、测试技术、数值计算技术和化学建模方法，涵盖了含硼燃料在固体火箭冲压发动机推进系统和固体微型推进器两种不同技术背景下的应用。既论述了原理性的基础科学研究，又讨论了实际应用中的工艺和工程问题。

本书内容丰富，实用性强。可供从事硼颗粒、含硼燃料及固体推进技术研究相关工作的工程技术人员、科研人员阅读使用，也可作为高等院校相关专业师生的教学、参考用书。

本书在中国科学院科学出版基金资助下，由科学出版社出版。

Effects of cavity position and structure on pulsed pressure oscillations

SU Wan-xing1,2, WANG Ning-fei2, LI Yao-jian1,CHEN Sheng-ze1,LI Jun-wei2, SUN Bing-bing2

(1.Research & Development Center, China Academy of Launch Vehicle Technology, Beijing 100076, China;2.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

In order to research the effects of cavity position and structure on pulsed pressure oscillations, four kinds of rocket motor models with different cavities were numerically studied via Fluent along with UDF(User Defined Functions). The flow structures and pulsed pressure oscillation characteristics were obtained, which can provide theoretical guidance for the design of grain structure and suppression of combustion instability. The results indicate that head end cavity is contributed to suppressing combustion instability. Middle cavity can easily induce vortex-driven-pressure oscillations, and the convergent middle cavity is better than divergent middle cavity in terms of the motor stability. After end cavity is harmful to motor stability because the end cavity can reduce the nozzle damping and induce vortex shedding under the pulsed condition. Therefore, the finocyl-end grain structure should be carefully considered in engineering design.

solid rocket motor；cavity；pulsed pressure oscillation；combustion instability

2015-02-11；

：2015-03-26。

苏万兴(1987—)，男，博士，研究方向为固体火箭发动机不稳定燃烧。E-mail:suwx_bit@163.com

V435

A

1006-2793(2015)06-0811-07

10.7673/j.issn.1006-2793.2015.06.011