行列式在解析几何中的应用

王紫萍

（贵州财经大学数学与统计学院，贵州 贵阳550025）

行列式是为表达n元线性方程组的一般解而引入的，有了行列式线性方程组的解就可通过简化的形式表示出来。本文就是根据行列式的这一特点，把行列式应用于几个解析几何问题的求解中，使这些问题的解可以用有规律的行列式表示出来。

在解析几何中，如果已知三角形三个顶点的坐标，求该三角形的面积；已知圆上三个点的坐标，求该圆的圆心；已知一个四面体的四个顶点坐标，求该四面体的体积；已知球上四个点的坐标，求该圆心的坐标，这几个问题用解析几何方法来求解是比较复杂的，下面通过行列式得到这这四个问题有规律的求解公式，这样上面的问题就转化为行列式的计算了。

公式一：已知三角形的三个顶点A(x1,y1)、B(x2,y2)、C(x3,y3)，则 三 角 形ABC的 面 积的绝对值.

证明：(如图1)把三角形ABC看成空间中在平面XOY面上的三角形

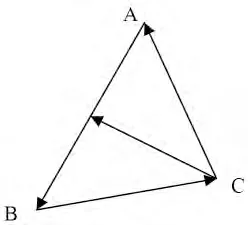
图1

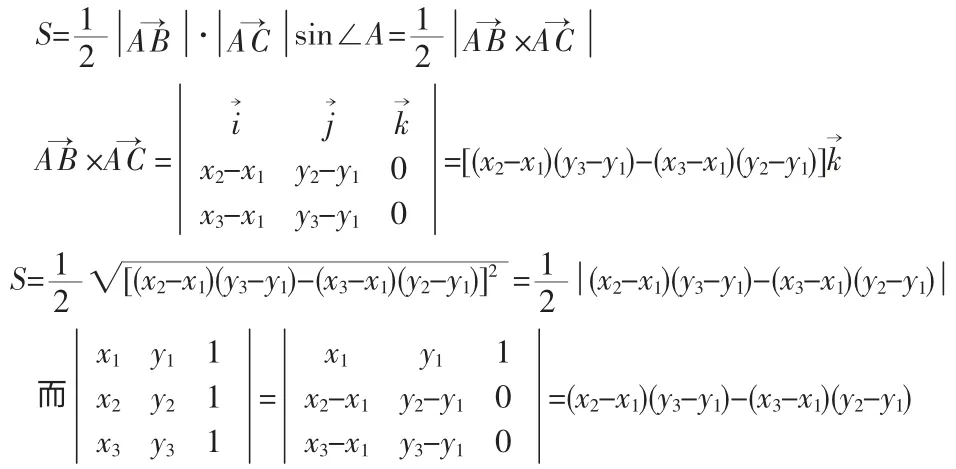
公式二：已知四面体四个顶点A(x1,y1,z1)、B(x2,y2,z2)、C(x3,y3,z3)、D(x4,y4,z4)则该四面体的体积为：的绝对值

证明：由向量混合积的定义及立体几何中四面体与相应的平行六面体的体积的关系，见[1]的绝对值

而

故公式二得证。

公式三：已知平面圆上三点A(x1,y1)、B(x2,y2)、C(x3,y3)，则圆心坐标为：

证明：由圆的方程(x-a)2+(y-b)2=R2可知在一般方程2ax+2by+c=x2+y2中(a,b)为圆心坐标，把已知三点坐标代入一般方程：

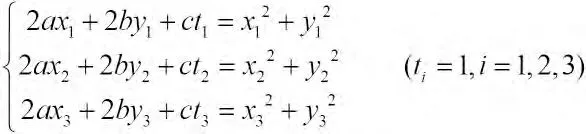
由Gramer法则解上面的方程组得圆心的横坐标公式如上,同理得圆心的纵坐标公式。

公式四：已知球上不共面四点A(x1,y1,z1)、B(x2,y2,z2)、C(x3,y3,z3)、D(x4,y4,z4)，其球心O(x y z)可按下列公式求得

证明：由球面方程(x-a)2+(y-b)2+(z-c)2=R2可知在

一般方程中2ax+2by+2cz+g=x2+y2+z2(a,b,c)为球心坐标把四点坐标代入一般方程：

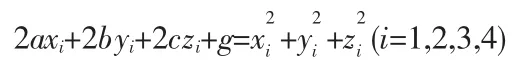
用Gramer法则解该线性方程组类似公式三的处理即可求得球心坐标公式如上。

以上四个公式中行列式的坐标排列均是有规律的，这样有了点的坐标后由这些点组成图形的三角形的面积、四面体的体积、圆的圆心和球的球心就可方便地代入以上公式中进行求解了。

［1］居余马,等.线性代数[M].2版.北京：清华大学出版社,2002.

［2］同济大学数学教研室,主编.高等数学[M].4版.北京：高等教育出版社,2002.