算法设计和分析的教学探索
王修君,高 艳,郑 啸
(安徽工业大学 计算机科学与技术学院,安徽 马鞍山 243002)
算法设计和分析的教学探索
王修君,高 艳,郑 啸
(安徽工业大学 计算机科学与技术学院,安徽 马鞍山 243002)
算法设计和分析是计算机专业的一门核心基础课程。以经典快速排序算法平均比较次数的两种分析方法作为切入点,多角度分析经典问题有助于学生深刻理解算法本质;对经典问题采用不同的分析手段而得到同样的答案这个过程,有助于学生体会分析手段多样性和算法分析之美。
算法分析;快速排序算法;平均比较次数分析
算法设计与分析课程是计算机专业核心课程之一。现有的算法设计与分析课程的教学过程往往过于强调经典算法:即让学生懂得某些经典算法的每一步骤细节和大概采用了什么样的算法设计策略等,最终目的是让学生可以用某种编程语言实现经典算法。
考虑到学习是一个由简单到复杂,再从复杂到简单的过程,而理解一个算法的本质特征只有通过对算法的细致分析才可以达到;[1]同时考虑到在选择算法解决实际问题时,最为重要的是所选算法的性能,[2-3]而掌握算法的性能知识不能靠死记硬背。因此多角度的算法性能分析在算法课程教学过程中起着相当重要的作用。笔者通过引入一个经典的快速排序算法的性能分析,展现算法性能的多角度分析,以帮助学生体会和理解算法的多行伪码中的本质,掌握算法的特性,体会算法设计与分析中的数学之美。
一、经典快速排序算法的多角度分析
经典的快速排序算法[3-5]如下:
算法输入:n个元素互异的列表S={x1,…,xn}
算法输出:排序后的S
Step 1. 如果S中只有0个或1个元素,则直接返回;否则继续。
Step 2. 随机选择S中的一个元素xt,t∈{1,2,…,n}作为划分元素。
Step 3. 将S中除xc外的其他元素与xc做比较,并划分S-{xc}为如下两个子列表S1,S2;a)S1是S中所有比x1小的元素构成的列表;b)S1是S中所有比x1大的元素构成的列表。
Step 4. 对S1,S2快速排序。
Step 5. 返回列表S1,x1,S2。
针对该经典的快速排序算法,本文将给出两种不同的分析方法来分析平均比较次数。[2,4]。为了表述方便,我们令Cn表示有n个元素的列表进行快速排序算法的平均比较次数。
二、基于递推关系式的快速排序平均比较次数分析
分析快速排序算法的step1,显然针对只含有0个元素和1个元素的列表S不需要排序(本身就是有序的),可得C0=0,C1=0。对于S中含有两个以上元素的情况,分析快速排序算法的step2到step5步,可得如下递归式:
(1)
其中:1/n表示快速排序算法在step2中所选择的数xc是S中第i小的元素的概率(i∈{1,2,…,n})。因为xc为随机选择,所以xc是第 i大元素的概率相等(i∈{1,2,…,n})。
当xc是第i大的元素时,显然S中除去xc外的元素被分成两个子列表S1,S2。由于S1是S中所有比x1小的元素构成的列表,S2是S中所有比x1大的元素构成的列表,所以S1中含有i-1个元素,而S2中含有n-i个元素。此时显然对S的排序问题分解为对两个子列表S1,S2的排序问题。用快速排序对S1,S2排序的代价为Ci-1+Cn-i(快速排序算法中的step4)。 (1)式右边的最后一项n-1表示step(3)中xc与S中剩下的n-1元素的n-1次比较操作(经过n-1次比较操作后,才能得到S1,S2)。由此,得到递归式(1)。下面我们考虑如何找出满足递归式(1)的Cn的闭形式解。
对(1)式两边同乘以n,可得:
(2)
基于(2),我们可以得到:
(3)
将(2)式和(3)式做差,可以得到如下:
Cn/(n+1)-Cn-1/n=4/(n+1)-2/n
(4)
令B=Cn/(n+1),我们可以得到如下递归式:
Bn-Bn-1=4/(n+1)-2/n
(5)
其中B0=0,B1=1。求解出Bn的通项公式也就可以求解出Cn。显然有如下等式:
(Bn-Bn-1)+(Bn-1-Bn-2)+(Bn-2-Bn-3)+…+(B2-B1)+(B1-B0)=Bn
(6)
将(5)代入(6),可得Bn的通项公式如下:
(7)
由(7),可以获得Cn的通项公式为:
(8)
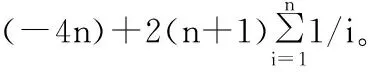
通过上面的基于递归分析方法的讲解,即对(1)~(7)式的每一步讲解,使得学生可以了解经典快速排序算法的伪码中每行代码的意义及其对算法性能影响。
三、基于数学期望的快速排序平均比较次数分析
不失一般性,假设列表S的有序形式为:x1 令随机变量Xx,j=1表示xi、xj在经典快速排序算法的某次递归中发生了比较,令Xx,j=0表示在经典快速排序算法的整个运行过程中xi和xj没有发生比较。显然,n个元素的快速排序算法的平均比较次数Cn可以表示如下: (9) 其中:E[·]表示数学期望运算。 令LR表示事件:在算法的某次递归中所选择的划分元素xc满足xc=xi或xc=xj;令M表示事件:在算法的某次递归中所选择的划分元素xc满足xi 下面我们考虑三种情况: 第一种情况:算法的某次递归中被选为划分元素xc 基于以上三种情况,并考虑到数值介于xi和xj之间有(j-i-1)个元素,分别为:Xi+1,…,Xj-1,加上xi和xj后,共有j-i+1个元素,我们有如下等式: (10) 综合(8)式和(9)式,并基于数学期望的线性,可得: (11) 根据(11)式中的对称性,上式可进一步化简为: Cn=2[1/n+2/(n-1)+…+(n-2)/3+(n-1)/2] (12) 通过基于数学期望的分析方法讲解,即通过(9)~(10)式的每一步分析讲解并与 (1)~(7)对照,学生可以深入了解经典快速排序算法中比较操作的特性及其与算法平均性能的数学关系。两种不同的分析方法对照和相同的分析结果可以进一步加深的学生对经典快速排序算法的伪码本质的了解,深刻体会分析方法的多样性与算法分析之美。 两种分析方法得到同样的结果:(12)式等价于(8)式。基于递推关系的分析方法,类似数学分析中的微分方程,利用的是经典快速排序算法中的递归机制,从小规模问题的解,去发现通向的解。基于数学期望的分析方法,直接求解有n个元素的快速排序算法的平均比较次数。该分析方法将数序期望的线性性和排序问题比较次数和的线性性结合,直接分析任意两个数进行比较操作的概率,以此获得单个期望的值,并求解最终的期望和。通过两种方法的讲解,显然可以给学生更多更深刻的启示,可以帮助学生更加深入地了解经典的快速排序算法。进一步,在学生了解和掌握这两种技术后,也可以很好地了解和分析其他快速排序的算法,如多路快速排序算法(即选择多个划分元素),体会算法分析之美,可以达到很好的教学效果。 [1]Ronald L.Graham, Oren Patashnik, Donald E.Knuth.具体数学[M].张凡,张明尧,译.北京:人民邮电出版社,2013. [2]Robert Sedgewick, Philippe Flajolet.算法分析导论[M].冯舜玺,李学武,裴伟东,等,译.北京:机械工业出版社, 2006. [3]Rajeev Motwani, Parbhakar Raghavan.随机算法[M].孙广中,等,译.北京:高等教育出版社, 2008. [4]Michael Mitzenmacher, Eli Upfal.概率与计算[M].史道济,等,译.北京:机械工业出版社,2007. [5]Thomas H.Cormen, Charles E.Leiserson, Ronald L.Rivest, Clifford Stein.算法导论[M].潘金贵,等,译.北京:机械工业出版社, 2006. (责任编辑 汪继友) Teaching Exploration of Algorithm Design and Analysis WANG Xiu-jun, GAO Yan, ZHENG Xiao (School of Computer Science and Technology, Anhui University of Technology, Ma’anshan 243002, Anhui, China) Algorithm design and analysis is the core course of computer science major. Taking the two analytical ways of average comparison times analysis and classical quick sort as breakthrough point and analyze from various perspectives are good for students to understand the algorithm better. The process of solving classic problems with different analytical methods and getting the same results is of great benefit for them to feel the variety of analytical skills and the beauty of algorithm analysis. algorithm analysis, quick sort, average comparison times analysis 2015-07-04 国家自然科学基金资助项目(61402008);安徽省自然科学基金资助项目(1408085QF128) 王修君(1983-),男,安徽枞阳人,安徽工业大学计算机科学与技术学院讲师,博士。 G642 A 1671-9247(2015)06-0085-02
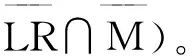
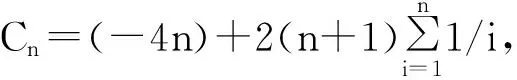
四、两种分析方法的教学意义

