薄壁加筋圆柱壳后屈曲分析方法研究

李庆亚,谭福颖,乔 玲,董萼良,费庆国

(1．东南大学 工程力学系, 南京 210096；2.江苏省工程力学分析重点实验室, 南京 210096)



薄壁加筋圆柱壳后屈曲分析方法研究

李庆亚1,2,谭福颖1,2,乔 玲1,2,董萼良1,2,费庆国1,2

(1．东南大学 工程力学系, 南京 210096；2.江苏省工程力学分析重点实验室, 南京 210096)

基于有限元采用非线性显式动力学分析方法，开展了轴压作用下薄壁加筋圆柱壳结构的后屈曲行为研究，比较了加筋圆柱壳结构筋条截面高宽比、蒙皮厚度、加筋疏密程度等结构几何参数对显式非线性算法计算屈曲临界载荷与隐式非线性算法计算结果的差异。研究结果表明，结构筋条质量与蒙皮质量之比大于0.4时，显式计算结果与隐式计算结果趋于一致，当筋条质量与蒙皮质量之比小于0.4时，显式算法计算结果与隐式算法计算结果会产生波动性差异。显式非线性分析能快速高效分析筋条质量与蒙皮质量之比大于0.4的薄壁加筋圆柱壳结构后屈曲行为。

加筋圆柱壳；后屈曲；显式动力学分析

0 引言

薄壁圆柱壳是工程中常用的壳体结构，在工业领域有着广泛的用途，这类薄壁结构的静强度失效很大一部分是由于其丧失稳定所引起的，受载时在未达到强度破坏前就发生失稳破坏[1-2]。为提高薄壁结构的承载力，在设计中通常增设筋条，薄壁加筋壳结构在飞行器设计中得到了广泛应用[3-5]。例如，运载火箭的主承力筒结构，加筋不仅可增加结构的整体刚度，发挥筋条和蒙皮的双重作用，而且还能提高结构的稳定性[6]，加筋壳结构的屈曲临界载荷远远超过同等质量的光滑壳体的临界载荷[7]。正交网格加筋圆柱壳是一种常见的加筋壳结构，其失稳过程一般表现为先局部失稳，随后整体失稳，结构丧失承载力。结构设计中，一般将结构整体失稳临界载荷作为设计载荷[8]，要预估一个薄壁加筋圆柱壳结构的整体失稳承载力就需要

解决结构的屈曲和后屈曲问题。在薄壁加筋结构屈曲后的破坏问题中，材料非线性和几何非线性交织在一起，要得到整体失稳承载力解析解十分困难，甚至不可能，对于这种结构，一般可通过3种途径获得：有限元法，半经验法以及工程算法。其中，半经验法需要通过大量试验研究找出规律，总结出简便的经验公式，但试验成本昂贵，且周期较长；工程算法存在一定局限性，对于大开口等非均匀性结构适应性较差。因此，在求解这类同时考虑几何非线性及材料非线性的后屈曲问题时，有限元法成了不可替代的分析手段[9]。

此类结构的后屈曲承载力计算方法一直是有限元分析的难点。非线性隐式分析方法，如基于Newton-Raphon迭代的弧长法[10-13]，该方法能够追踪整个结构的平衡路径，即能够跨越屈曲分叉点或极限强度点，较为准确有效的追踪整个失稳过程中的实际载荷、位移关系，而获得结构失稳前后的全部信息，可用于缺陷敏感型结构，但当结构出现局部屈曲后，计算步长将变得很小，导致计算时间激增甚至出现计算不收敛[15]；隐式动力学分析方法，若为获得高精度解，网格细化将大大增加计算成本，同时对于存在接触等非线性问题，也可能无法保证收敛；非线性显式后屈曲[14-16]分析可相对较快的得到结构的极限承载力，且计算所得失稳波形与试验失稳波形一致[16]，同时该方法稳健，不存在收敛问题，但计算可能受模型复杂程度，单元尺寸，加载速度等因素影响，屈曲临界载荷需通过试算获取[17]。目前，对于此类加筋柱壳结构，由于显式算法稳健，不存在收敛问题，可较快地获得结构后屈曲临界承载力。因此，更适于结构后屈曲分析。

本文基于有限元，利用非线性显式算法分析加筋圆柱壳结构后屈曲行为。分析了加筋圆柱壳进行有限元稳定计算屈曲临界载荷的影响因素，系统研究了结构几何参数改变，即结构筋条质量与蒙皮质量之比改变，非线性显式算法分析加筋圆柱壳结构临界屈曲载荷与隐式算法计算结果的差异，并给出了显式非线性算法分析的合理范围。

1 非线性显式后屈曲分析方法

1.1 显式时间积分

对于一个显式动力学分析，运动方程可表示为

Mü+I-P=0

(1)

式中M为质量矩阵；I为粘性效应项；P为外部激励作用；ü为节点加速度。

在任意时刻t，上述方程可视为考虑了惯性力项Mü，粘性效应项I，外载荷项P作用下的动力平衡方程。当惯性力足够小，可忽略时，公式即退化为静力学平衡方程。

在当前增量步开始时，计算加速度为

üt=(M)-1·(P-I)t

(2)

显式算法采用一个对角或者集中的质量矩阵，任何节点的加速度是完全取决于节点质量和作用在节点上的合力，求解加速度不必同时求解联立方程，使得节点计算的成本非常低。

对加速度在时间上进行积分采用中心差分方法，在计算速度的变化时，假定加速度为常数。应用这个速度的变化值加上前一个增量步中点的速度来确定当前增量步中点的速度：

(3)

速度对时间的积分，并加上在增量步开始时的位移，以确定增量步结束时的位移：

(4)

这样，在增量步开始时，提供了满足动力学平衡条件的加速度。得到了加速度，在时间上“显式地”前推速度和位移。所谓“显式”是指在增量步结束时的状态仅依赖于该增量步开始时的位移、速度和加速度。为了使该方法产生精确的结果，时间增量必须相当小，在增量步中加速度几乎为常数。由于时间增量步必须很小，一个典型的分析需要成千上万个增量步。因为不必同时求解联立方程组，所以每一个增量步的计算成本很低。大部分的计算成本消耗在单元的计算上，以此确定作用在节点上的单元内力。单元的计算包括确定单元应变和应用材料本构关系确定单元应力，从而进一步地计算内力。

1.2 显式算法收敛性

显式动力学分析运动方程中，粘性效应项：

(5)

(6)

节点位移泰勒展开：

(7)

(8)

由式(7)和式(8)可得：

(9)

(10)

将式(9)和式(10)代入动力学控制方程式(6)得：

(11)

由式(11)可看出，ut+Δt仅由ut和ut-Δt决定。因此，运动方程可直接求解，无需迭代，不存在收敛性问题。

2 算例研究

本文以薄壁加筋壳结构为0～90°正交加筋结构为研究对象，如图1所示。其几何尺寸如下：壳体直径D为1 000 mm，高度L为1 000 mm，共12根环向筋，79根纵向筋，筋条高度h为18 mm，筋条宽度tw为1.8 mm，蒙皮厚度ts为1.3 mm。整个结构均采用铝合金材料，材料弹性模量为6.8×104MPa，泊松比为0.33，材料密度为2.7×10-6kg/mm3。边界条件为一端固支，另一端仅有轴向位移。

2.1 加筋圆柱壳结构建模

正交加筋圆柱壳若采用实体建模分析，并获得满意的分析精度，则模型的求解自由度将急剧增加，变成海量计算，对计算机硬件要求较高[18]。为准确模拟结构屈曲失稳行为，必须根据结构的主要失效行为或模式进行模型简化，以达到准确模拟的目标[19]。非线性屈曲分析得到的承载力为整体结构发生屈曲时的临界力，当结构发生局部失稳后，整体结构还有继续承载的能力，直到发生整体失稳以及材料发生塑性变形为止[20]。传统的结构简化，即圆筒壳采用壳(Shell)单元模拟，筋条采用梁(Beam)单元模拟，壳体和筋条之间采用约束绑定在一起，这种建模可准确有效的模拟结构的线性刚度，但却忽略了筋条的局部截面平动和转动，不能准确模拟结构的后屈曲行为[19]。由于正交加筋圆柱壳通常使用较薄的蒙皮和筋条，结构上体现为板壳特性[18]。因此，若筋条也采用壳(shell)单元建模，蒙皮和筋条就构成壳-壳(shell-shell)模型，如图2所示。模型中蒙皮和筋条之间融合成一个整体，无需采用约束绑定在一起，只需在不同区域赋予不同厚度和属性。采用此方法建模，可准确模拟结构的失稳过程。

2.2 非线性显式后屈曲分析

模型下端面固支，上端面节点刚性耦合至中心参考点，并约束除轴向位移外的其余自由度，在参考点上施加轴向位移载荷，加载总位移为20 mm，采用显式非线性分析模拟准静态加载。本文采用四节点壳单元对模型进行离散，该单元为四节点减缩积分单元，计算精度高，时间短。

表1讨论了显式分析给定模型对单元尺寸的依赖性，图3给出了给定模型不同单元尺寸下显式分析得到的结构轴向位移-载荷曲线及计算CPU耗时。不同单元尺寸下计算所得临界载荷存在一定差别，后屈曲路径也各不相同。结果表明，显式算法计算结构临界载荷对单元尺寸有一定的依赖。

图1 正交加筋模型整体图Fig.1 Diagram of stiffened cylindrical shell

图2 壳-壳模型局部图Fig.2 Diagram of shell-shell model

表2讨论了显式分析给定模型对加载时间的依赖性，图4给出了显式分析给定模型不同加载时间对临界载荷的影响，以消除显式分析模拟准静态加载的动态效应，同时给出了不同加载时间下的计算CPU耗时。不同加载时间对计算临界载荷影响较小，增大加载时间，后屈曲路径趋于一致。结果表明，显式算法计算结构临界载荷对加载时间依赖性不强。

表1 单元尺寸依赖性计算结果Table1 Result of dependence of element size

表2 加载时间依赖性计算结果Table2 Result of dependence of loading time

图3 不同单元尺寸下轴向位移-载荷曲线Fig.3 Load-displacement curves with varying element sizes

图4 不同加载时间下轴向位移-载荷曲线Fig.4 Load-displacement curves with varying loading time

综合计算成本和计算精确度，模型计算选择单元尺寸为30 mm，加载时间为200 ms。图5给出了显式算法下给定模型计算应力云图，结构主要在靠近加载段发生屈曲变形。图6给出了与其相同单元尺寸下隐式弧长算法计算轴向位移-载荷曲线。显式算法与其相同单元尺寸下隐式弧长算法计算所得屈曲临界载荷分别为2 121.76、2 108.88 kN，表明显式算法计算结果的可靠性。

图5 显式分析下结构应力云图Fig.5 Structure stress nephogram under explicit analysis

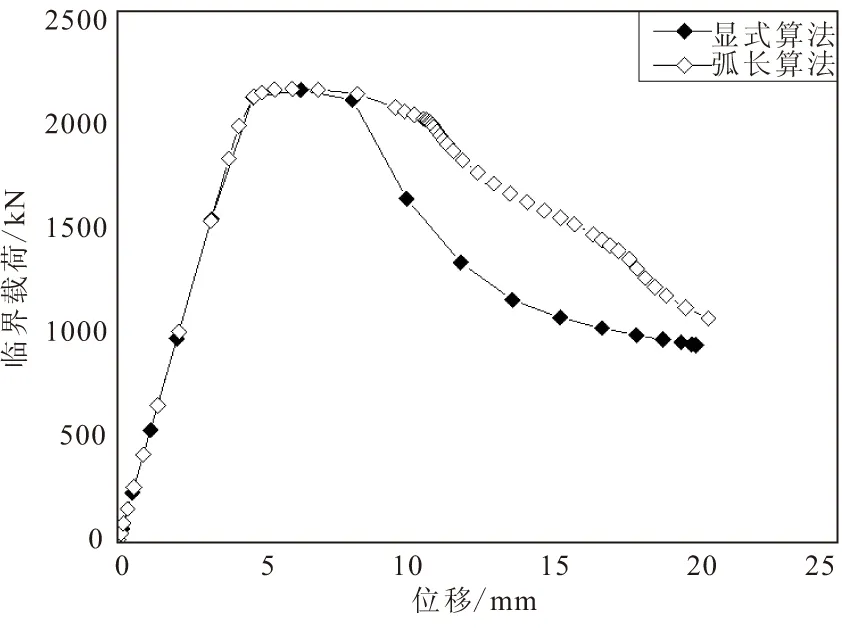
图6 显式算法与隐式弧长算法轴向位移-载荷曲线Fig.6 Load-displacement curves under explicit analysis and arc-length method

3 方法对比

本文研究了等体积加筋柱壳结构，改变其中某一几何参数，如筋条截面高宽比、蒙皮厚度或加筋疏密度等，即改变结构筋条与蒙皮质量之比，采用非线性显式算法，通过调试单元尺寸计算结构的屈曲临界载荷，考虑计算成本，选择合适单元尺寸，并与相同单元尺寸下隐式非线性算法计算结果进行比较。

3.1 筋条截面高宽比

为研究筋条截面高宽比改变后显式算法计算结构屈曲临界载荷与隐式算法计算结果的差异，在结构等体积下，保持筋条数和蒙皮厚度不变，改变筋条截面高宽比，采用显示算法分析得到不同高宽比下临界载荷，并与采用隐式算法计算所得结果进行比较。图7给出了不同筋条截面高宽比两种算法的计算结果及差异。图7中，字母L表示结构失稳模态为局部失稳；G表示结构失稳模态为整体失稳。

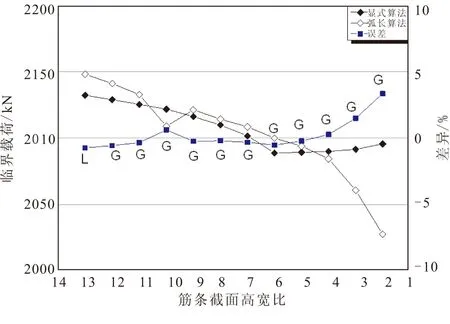
图7 不同截面高宽比两种算法计算结果及差异Fig.7 Results and difference between two methods with varying section ratio

由图7分析可知，随着筋条截面高宽比的下降，结构失稳模态由局部失稳转为整体失稳过程中，显式算法计算所得屈曲临界载荷与隐式算法计算所得结果相差不大，只有高宽比降至最低时，其计算结果与隐式计算结果相差稍显增大，但不超过5%，且产生差异最大处与屈曲模态转变处不一致。

改变筋条截面高宽比，结构筋条质量与蒙皮质量之比不变，比值为0.916，显式算法计算所得临界载荷与隐式算法计算结果差异很小。

3.2 蒙皮厚度

为研究蒙皮厚度改变后显式算法计算结构屈曲临界载荷与隐式算法计算结果的差异，在结构等体积下，固定环筋数为9，纵筋数为60，分别研究两种筋条截面高宽比：高宽比3和高宽比10，蒙皮厚度从1.4 mm增至2.4 mm，即筋条质量与蒙皮质量之比由0.786降至0.042过程中，采用显式算法计算屈曲临界载荷和采用隐式算法计算所得结果进行对比。

图8给出了筋条截面高宽比为10情况下，随着蒙皮厚度增加，结构失稳模态由局部失稳转为整体失稳过程中，显式算法与隐式算法计算屈曲临界载荷及两种算法之间的差异。筋条截面高宽比为10情况下，当蒙皮厚度未达到2.1 mm时，筋条质量与蒙皮质量之比大于0.2，显式算法与隐式算法计算临界载荷相差无异，当蒙皮厚度大于2.1 mm时，筋条质量与蒙皮质量之比小于0.2，显式算法与隐式算法计算临界载荷出现了大于10%的差异，差异呈现先增大、后减小的趋势，且差异的产生处与屈曲模态转变处不一致。

图8 高宽比为10两种算法计算结果及差异Fig.8 Results and difference between two methods when section ratio is 10

图9给出了筋条截面高宽比为3的情况下，随着蒙皮厚度增加，结构屈曲模态始终为整体屈曲过程中，显式算法与隐式算法计算屈曲临界载荷及两种算法之间的差异。当蒙皮厚度未达到1.8 mm时，筋条质量与蒙皮质量之比大于0.4，显式算法与隐式算法计算临界载荷相差无异，当蒙皮厚度大于1.8 mm时，筋条质量与蒙皮质量之比小于0.4，显式算法与隐式算法计算临界载荷差异逐步增大，最大差异超过15%。差异也是呈现先增大后减小的趋势。

综合两种不同筋条截面高宽比结构计算结果，结果表明，改变蒙皮厚度，当筋条质量与蒙皮质量之比大于0.4时，显式算法计算屈曲临界载荷与隐式算法计算结果几乎一致；当筋条质量与蒙皮质量之比小于0.4时，显式算法计算屈曲临界载荷与隐式算法计算结果存在波动性差异，且差异产生并非由于屈曲模态转变而引起的。

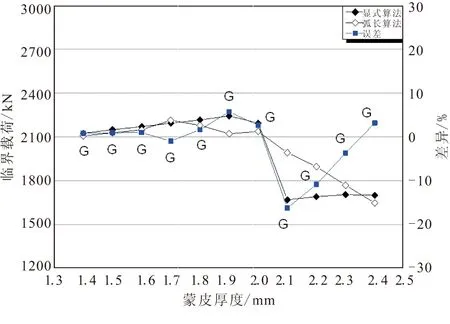
图9 高宽比为3两种算法计算结果及差异Fig.9 Results and difference between two methods when section ratio is 3

3.3 筋条疏密程度

为研究筋条疏密程度改变后显式算法计算结构屈曲临界载荷与隐式算法计算结果的差异，分别研究了结构等体积下减少环向筋条数目，减少纵向筋条数目，以及同时减少环纵向筋条数目这3种情况下，显式算法计算屈曲临界载荷与隐式算法计算结果的比较。

3.3.1 减少环筋数目

环筋数目对结构承载力的贡献较小，当环向筋数目减少，环向筋间距增大，每个筋格纵向筋长度变长，容易出现蒙皮和纵向筋局部失稳的情形。为研究环向筋数目减小对显式算法计算结构屈曲临界载荷与隐式算法计算结果的差异，在结构等体积下，固定纵向筋数为90根，分别研究两种筋条截面高宽比：高宽比3和高宽比10。环筋数由9根递减至2根，即筋条质量与蒙皮质量之比由0.567降至0.373的过程中，显式算法计算临界载荷与隐式算法计算结果的对比。

图10给出了筋条截面高宽比为10，随着环筋数降低，结构屈曲模态始终为局部屈曲过程中，显式算法与隐式算法计算临界载荷及两者之间差异。当环筋数递减至4根时，筋条质量与蒙皮质量之比为0.423，显式算法计算临界载荷与隐式算法计算结果相差无异。当环筋数降至4根以下，即筋条质量与蒙皮质量之比小于0.4时，显式算法计算所得临界载荷与隐式算法计算临界载荷相差较大，最大差异超过了20%，且计算差异的产生处与结构屈曲模态转变处不一致。

图10 高宽比为10两种算法计算结果及差异Fig.10 Results and difference between two methods when section ratio is 10

图11给出了筋条截面高宽比为3，随着环筋数降低，结构屈曲模态由整体屈曲转变为局部屈曲过程中，显式算法与隐式算法计算临界载荷及两者之间差异。当环筋数目递减至3根时，即筋条质量与蒙皮质量之比为0.398，显式算法计算临界载荷与隐式算法计算临界载荷相差无异。当环筋数为2时，筋条质量与蒙皮质量之比为0.373，显式算法计算结果与隐式算法计算结果相差较大，差异超过20%。

图11 高宽比为3两种算法计算结果及差异Fig.11 Results and difference between two methods when section ratio is 3

综合以上两种不同筋条截面高宽比情况，结果表明，减少环筋数，当筋条质量与蒙皮质量之比大于0.4时，显式算法计算屈曲临界载荷与隐式算法计算结果几乎一致；当筋条质量与蒙皮质量之比小于0.4时，显式算法计算屈曲临界载荷与隐式算法计算结果存在一定差异，且差异产生并非由于屈曲模态转变而引起的。

3.3.2 减少纵筋数目

纵筋数目对结构承载力贡献较大，但当纵筋数目减少，筋格环向筋长度变长，也容易出现局部失稳。为研究纵向筋数目减小对显式算法计算结构屈曲临界载荷与隐式算法计算结果的差异，现等体积下，固定环筋数目为9根，分别研究两种筋条截面高宽比：高宽比3和高宽比10。纵筋数由120根以每10根递减至10根，即筋条质量与蒙皮质量之比由1.548降至0.186的过程中，显式算法计算临界载荷与隐式算法计算结果的比较。

图12给出了筋条截面高宽比为10，随着纵筋数降低，结构屈曲模态由整体屈曲转变为局部屈曲过程中，显式算法与隐式算法计算临界载荷及两者之间差异。当纵筋数降至50根时，此时筋条质量与蒙皮质量之比为0.472，显式算法计算临界载荷与隐式算法计算结果相差无异。当纵筋数低于40根时，筋条质量与蒙皮质量小于0.4，显式算法与隐式算法计算结果出现差异，差异呈现先增大、后减小的趋势，差异产生处与屈曲模态转变处不一致。

图12 高宽比为10两种算法计算结果及差异Fig.12 Results and difference between two methods when section ratio is 10

图13给出了筋条截面高宽比为3，随着纵筋数降低，结构屈曲模态由整体屈曲转变为局部屈曲过程中，显式算法与隐式算法计算临界载荷及两者之间差异。纵筋数为50～120根时，筋条质量与蒙皮质量之比大于0.4，显式算法计算精度较高，当纵筋数降至30根时，此时筋条质量与蒙皮质量之比为0.314，显式算法计算结果与隐式算法计算结果存在一定差异，差异超过15%。差异也是随着筋条数降低，呈现出先增加、后降低的趋势，差异产生处与结构屈曲模态转变处一致。

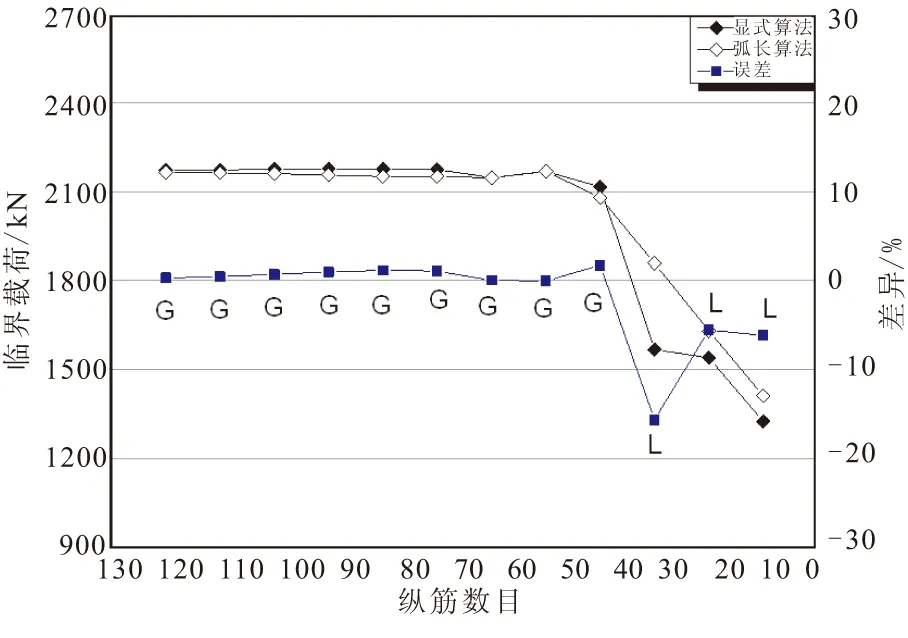
图13 高宽比为3两种算法计算结果及差异Fig.13 Results and difference between two methods when section ratio is 3

综合以上两种筋条截面高宽比情况，结果表明，减少纵筋数，当筋条质量与蒙皮质量之比大于0.4时，显式算法计算临界载荷与隐式算法计算结果几乎一致；当筋条质量与蒙皮质量之比小于0.4时，显式算法计算屈曲临界载荷与隐式算法计算结果存在波动性差异，且差异产生并非由于屈曲模态转变而引起的。

3.3.3 减少环筋和纵筋数目

环纵筋数目同时减少，筋格尺寸增大，容易出现桁框内蒙皮局部失稳。为研究环向和纵向筋数目同时减小对显式算法计算结构屈曲临界载荷与隐式算法计算结果的差异，现等体积下环筋数目由9根递减至2根，纵筋数由90根以8、6、6循环依次递减至12根，即筋条质量与蒙皮质量之比由0.567降至0.081过程中，分别研究了两种筋条截面高宽比：低高宽比3和高高宽比10，显式算法计算结果与隐式算法计算结果的对比。

图14给出了筋条截面高宽比为10，随着环纵筋数同时降低，结构屈曲模态始终为局部屈曲过程中，显式算法与隐式算法计算临界载荷及两者之间差异。当环筋数大于5根，纵筋数大于32根，显式算法计算临界载荷与隐式算法计算结果相差无异；当环筋数降至5根，纵筋数降至32根时，即筋条质量与蒙皮质量之比为0.243，此时显式算法与隐式算法出现很大差异，结果差异近20%。随着环纵筋数目的继续减少，显式算法与隐式算法计算差异呈现先降低后增长的趋势。

图15给出了筋条截面高宽比为3，随着环纵筋数同时降低，结构屈曲模态由整体屈曲转变为局部屈曲过程中，显式算法与隐式算法计算临界载荷及两者之间差异。当环筋数大于7根，纵筋数大于46根，显式算法计算临界载荷与隐式算法计算结果相差无异，此时筋条质量与蒙皮质量之比为0.386，显式算法计算结果与隐式算法计算结果相差近3%。随着筋条数的逐步减少，差异呈现先增大后减少再增大的趋势，最大差异接近20%，且差异产生处与屈曲模态转变处一致。

图14 高宽比为10两种算法计算结果及差异Fig.14 Results and difference between two methods when section ratio is 10

图15 高宽比为3两种算法计算结果及差异Fig.15 Results and difference between two methods when section ratio is 3

综合以上两种筋条截面高宽比情况，结果表明，同时减少环纵筋数，当筋条质量与蒙皮质量之比大于0.4时，显式算法计算临界载荷与隐式算法计算结果几乎一致；当筋条质量与蒙皮质量之比小于0.4时，显式算法计算屈曲临界载荷与隐式算法计算结果存在波动性差异，且差异产生并非由于屈曲模态转变而引起的。

4 结论

基于非线性显式算法，以正交加筋圆柱壳结构为例，采用壳-壳单元对加筋圆柱结构简化建模，分析加筋柱壳结构后屈曲行为。针对加筋柱壳失稳极限承载力，研究了针对给定正交加筋壳结构，显式非线性算法对单元尺寸以及加载时间的依赖性。计算结果表明：对于给定结构，显式非线性算法对单元尺寸有一定的依赖性，对加载时间依赖性不强。比较了模型结构几何参数，如筋条截面高宽比、蒙皮厚度、筋条疏密程度等改变对计算其临界载荷与隐式算法计算结果差异的影响。计算结果表明，对于筋条质量与蒙皮质量之比大于0.4的结构，显式非线性算法计算所得临界载荷与隐式非线性算法计算临界载荷趋于一致；对于筋条质量与蒙皮质量之比小于0.4的结构，显式非线性算法与隐式非线性算法计算结果存在一个波动性的差异，且波动性差异并非由于结构屈曲失稳模态转变而产生。显式非线性算法能够快速高效求解筋条质量与蒙皮质量之比大于0.4的加筋圆柱壳结构后屈曲临界载荷。

[1] 谭福颖,乔玲,等.基于广义梁理论的薄壁加筋圆柱壳稳定性分析[J].东南大学学报,2013,43(5):1062-1067.

[2] 龙连春,赵斌,陈兴华.薄壁加筋圆柱壳稳定性分析及优化[J].北京工业大学学报,2012,38(7):997-1003.

[3] 梁东平,徐元铭,彭兴林.复合材料格栅加筋板布局优化设计[J].固体火箭技术,2008,31(5):527-531.

[4] 辛星.复合材料网格圆柱结构减重设计优化[J].固体火箭技术,2013,36(2):243-246.

[5] 何景轩,何国强,任明法.复合材料格栅结构屈曲特性分析[J].固体火箭技术,2008,31(4):389-392.

[6] 龙连春,李洋,赵斌.加筋圆柱壳屈曲与后屈曲分析[A].力学与工程应用,2012,145-147.

[7] 龙连春,陈兴华,等.矩形加筋圆柱壳轴压屈曲承载力优化[J].中国农业大学学报,2009,14(4):124-130.

[8] 王斌,王博,等.基于显式有限元算法的网格加筋圆柱壳后屈曲承载能力优化[Z].中国力学大会2011暨钱学森诞辰100周年纪念大会.哈尔滨,2011.

[9] 朱志红.薄壁加筋壳结构稳定性分析[D].电子科技大学,2010.

[10] Hellweg H B,Crisfiela M A.A new arc-length method for handling sharp snap-back[J].Computers and Structures,1998,66(5):704-709.

[11] 熊晓枫.薄壁结构非线性有限元数值计算及其稳定性分析研究[D].西北工业大学,2006.

[12] 周凌远,李乔,等.改进弧长法求解屈曲问题[J].西南交通大学学报,2011,46(6):922-925.

[13] 史旭东.板壳非线性有限元稳定性分析[D].南京航空航天大学,2005.

[14] 郝鹏,王博,李刚,等.基于缺陷敏感性分析的加筋圆柱壳结构设计[J].应用力学学报,2013,30(3):344-349.

[15] 郝鹏,王博,李刚,等.基于代理模型和等效刚度模型的加筋柱壳混合优化设计[J].计算力学学报,2012,29(4):481-486.

[16] Takaya Kobayashi,Yasuko Mihara,Fumio Fujii.Path-tracing analysis for post-buckling process of elastic cylindrical shells under axial compression[J].Thin-Walled Structures,2012,61:180-187.

[17] Huang C,Zhang X,Wang B,et al.Optimization of an axially compressed ring and stringer stiffened cylinder structure with explicit FEM method[C]// 6th China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems.Kyoto,2010.

[18] 余成斌.格栅加筋回转壳稳定性能分析及优化[D].南昌航空大学.2013.

[19] 张国凡,段世慧,吴存利.基于有限元的加筋板结构后屈曲分析方法研究[J].强度与环境,2013,40(2):43-50.

[20] 李洋.薄壁加筋结构屈曲分析及优化设计[D].北京工业大学,2013.

(编辑：薛永利)

Comparative study on post-buckling analysis method of thin-walled stiffened cylindrical shell

LI Qing-ya1,2,TAN Fu-ying1,2,QIAO Ling1,2DONG E-liang1,2,FEI Qing-guo1,2

(1.Department of Engineering Mechanics,Southeast University, Nanjing 210096,China)(2.Jiangsu Key Laboratory of Engineering Mechanics,Nanjing 210096,China)

The post-buckling behavior of thin-walled stiffened cylindrical shell structures under axial compression was studied based on FEA by nonlinear explicit dynamic method,and the critical buckling load was compared with nonlinear implicit method when changing the structural geometric parameters,such as cylindrical shell ribs sectional aspect ratio,skin thickness,and the degree of density.The results show that: the mass ratio of the ribs and the skin is greater than 0.4,the calculation results between the explicit and implicit methods are consistent.When the mass ratio of the ribs and the skin is less than 0.4,the calculation results between the explicit and implicit methods present a volatility differences.Explicit nonlinear analysis is a fast and efficient analysis method for the post-buckling behavior of thin-walled stiffened cylindrical shell structures when the mass ratio of the ribs and the skin is greater than 0.4.

stiffened cylindrical shell;post-buckling;explicit dynamic method

2014-04-17；

：2014-06-29。

国家自然科学基金(10902024；11202051)；教育部博士学科点基金(2013009212 0039)；教育部新世纪优秀人才支持计划(NCET-11-0086)。

李庆亚(1990—)，男，硕士生，研究方向为运载火箭主承力筒后屈曲。E-mail：kingyalee@163.com

董萼良。E-mail：eldong@seu.edu.cn

V414

A

1006-2793(2015)04-0541-08

10.7673/j.issn.1006-2793.2015.04.018