金属颗粒燃烧过程表面曳力变化的数值研究

贺 征, 刘丛林，李 卓，顾 璇，郜 冶

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)



金属颗粒燃烧过程表面曳力变化的数值研究

贺 征, 刘丛林，李 卓，顾 璇，郜 冶

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)

为了考察固体火箭发动机内金属颗粒在生长过程中所产生的非球颗粒受力问题，采用数值模拟方法，在通过和文献及实验数据对比验证确定最佳计算模型的基础上，对初始半径为100 μm的铝颗粒处于不同相变燃烧阶段时所受到的曳力进行对比分析。结果表明，在多相流场中，非球颗粒表面可能存在两处压力为零的点，曳力系数普遍大于其当量直径颗粒的计算结果，当颗粒外形严重偏离球体时，经验公式计算所得的曳力系数有失精准，需进行相应修正。

金属颗粒；非球颗粒；燃烧；当量直径；曳力系数

0 引言

含金属颗粒的气固多相流是一种十分典型的多相流动。其中，分散相颗粒的动力学特性是工程应用中不可忽视的重要问题。当金属颗粒在流场中发生相变燃烧时，部分凝相将回落到颗粒表面，令其转变为不规则的非球体[1-2]，导致动力学特性发生一系列改变，进而影响整个多相流场的流动特性。而经典的颗粒受力理论是以规则球形为基础进行推导的，在实际应用中，不可避免地会产生一定偏差[3]。采用数值模拟方法，针对固体火箭发动机内，金属颗粒在生长过程中，因形状变化而引起受力改变的现象进行研究，对工程应用有一定参考作用。

早期的研究集中于球形液滴，并已经形成了成熟的经验关系式[4-5]。相对而言，对于非球形颗粒的研究开展的较少，Komar[6]、Loth[7]开展了圆柱体的阻力系数计算，并推导其阻力系数的变化。Sabine[8]等研究了若干颗粒结合时的阻力系数。Youngho and Changhoon[9]模拟计算了变形颗粒的的阻力和升力，发现其数值与颗粒的形变有直接关系。

目前，对于非球形不规则颗粒的数值计算，大多采用近似球形的处理方法[10]。这种近似过程的实现主要通过2个途径进行——引入等效直径或引入球形度。其中，前者应用的较为广泛，最常用的等效直径是等体积直径dv[11]。引入dv后，认为非球颗粒与其等效直径相同的球形颗粒受力相同，文中对这2种计算结果进行了对比分析。

1 物理模型

铝颗粒初始进入发动机时，其表面将迅速被氧化物所包裹，颗粒形状已经发生变化[12]，颗粒表面积以及同来流方向相垂直的横截面面积与球形颗粒不再相同，受力状态发生一定改变。

Merrill[13]研究了铝颗粒在固体火箭发动机环境中的燃烧过程，对Al2O3的生成过程做了仔细的推导和计算。相比于传统的R2定律，Merrill所得结果更加符合实际情况。以Merrill的研究结果为基础，对初始半径为100 μm的铝颗粒在热燃气流中处于不同相变燃烧阶段时的受力问题进行了分析，计算工况列于表1中。

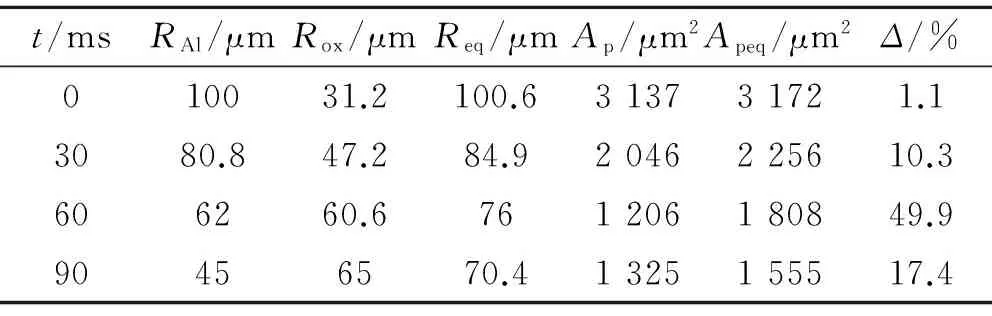
表1 计算工况汇总Table1 Summary of computation cases

其中，t表示颗粒进入发动机燃烧室中的时间，RAl、Rox分别表示颗粒中铝的半径和与其相连的球形氧化物半径，Req为其相应的等体积半径，Ap、Apeq分别代表真实颗粒与等体积颗粒垂直于来流方向的横截面面积。统计表明，随颗粒燃烧状态的改变，等体积颗粒的横截面面积偏离真实颗粒的水平(Δ%)较大，最大相差49.9%，即便在颗粒初始进入流场时，也有1.1%的差别。

利用Fluent软件，对流场中颗粒的受力状态进行分析。颗粒半径r取为100 μm，为准确计算颗粒附近流场的流动状态，同时兼顾计算网格的数量，计算区域中，取平行于来流方向的长l为30r，即3 mm，垂直于来流方向的宽d为20r，即2 mm。颗粒置于流场中，靠近来流方向，中心与入口边界相距l1为10r，即1 mm。采用非正交网格进行划分，颗粒的近壁面处做加密处理，最小网格尺寸为5 μm，最大为100 μm，总网格数约为22万，如图1所示。

2 控制方程

假设来流是稳态的，其物理性质在运动过程中不发生变化，计算的控制方程为

▽·U=0

(1)

▽·(ρUU)=-▽p+μ▽2U

(2)

为简化模拟条件，不考虑气固两相间的传热，取空气为介质，密度为1.225kg/m3，粘性系数为1.789×10-5kg/(m·s)，流场入口速度取发动机燃烧室环境下的均值，为20m/s，流场出口为自由边界。

颗粒曳力系数Cd由颗粒所受到的阻力FD来定义[14]:

(3)

颗粒所受的阻力FD由2部分组成：颗粒表面压强梯度所产生的压力阻力，以及流体粘性所产生的粘性阻力。因此，颗粒的曳力系数也分为2部分——压力曳力系数和粘性曳力系数。

随颗粒相变燃烧的进行，尺寸不断改变，颗粒雷诺数Rep随之发生变化，以当量直径计，对应于t=0、30、60、90 ms时，Rep分别为274.0、116.2、10.4、9.6。

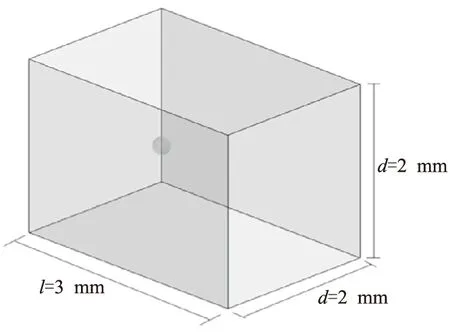
(a)三维计算模型

(b)模型网格分布

3 计算结果与分析

3.1 模型验证

为验证各种湍流模型对计算结果的影响，首先对颗粒在1≤Rep≤1 000范围内的受力问题进行计算，以寻求最佳计算模型。采用的湍流模型包括realizablek-ε模型、RNGk-ε模型、standardk-ε模型和Spalart-Allmadas模型。

验证工作共包括32种工况，颗粒雷诺数Rep分别取为1、10、30、50、100、300、500及1 000，流场工质均为空气。文献[15]与[16]分别对Rep在18.7～87.3以及10～809.7范围内的颗粒曳力系数做了实验，文献[17]采用直接模型方法对Rep在10～300范围内的颗粒曳力系数进行了计算，以上结果均可作为参考。对于Rep=1和1 000的工况，尚无实验可询，取标准阻力曲线值相对比。

图2直观地反映了各模型的计算结果与标准阻力曲线和文献实验值的对比。当颗粒雷诺数Rep<100时，除Spalart-Allmadas模型外，其余3种模型均能很好地与标准阻力曲线相符。其中，realizablek-ε模型下各种情况的计算值与标准阻力曲线值的均方差为3.63，RNGk-ε模型的均方差为3.77、标准k-ε模型为4.05，而Spalart-Allmadas模型的均方差则高达14.28。当颗粒雷诺数Rep较高(>100)时，4种模型的计算值与标准曲线相比，差别都很大，但可较好符合文献[2-3]的实验结果。为兼顾较大范围内的计算，选择Realizablek-ε模型进行颗粒受力分析的数值模拟更为适宜。

图2 不同湍流模型的计算结果与文献结果的对比Fig.2 Computed results of different models vsreference results

3.2 颗粒周围流场压力与速度分布对比分析

在多相流场中，颗粒会随着流动发生位置偏转，为分析真实颗粒与球形当量径颗粒的差别，取典型状态——颗粒在垂直来流方向投影面最大时进行计算。不同时刻下，真实颗粒与当量直径颗粒流场附近的压力与速度分布如图3、图4所示。在迎风方向上，颗粒表面附近的气流速度由流场入口沿颗粒中心轴线方向迅速降低，在颗粒表面处出现驻点，同时当地压力达到最高值。颗粒背风面处也存在着一个速度为零的区域，同时当地压力降到最低值。流场中颗粒背风域形成长长的流动尾迹表明，迎风面的气流速度衰减梯度明显大于背风面的速度增长梯度。

观察颗粒表面的气流变化可发现，气流由驻点的零速度向滞止点的零速度转变过程是气流速度沿颗粒表面先增加，至颗粒与来流相垂直的轴线中心处，速度达到最大值，且此值大于流场的平均速度；之后，因颗粒背风面存在涡流区，气流速度逐渐降低，至颗粒平行于来流的轴线中心处，再次降为0。在所计算的4种雷诺数下，颗粒迎风面与背风面的压差达550 Pa左右，颗粒表面处的最大速度值比流场平均速度高10%。随着颗粒在流场中相变燃烧的进行，当颗粒尺寸减小时，颗粒背风域所形成的流动尾迹随之变短，同时颗粒附近的压力变化区(以-50～50 Pa计)半径减小。

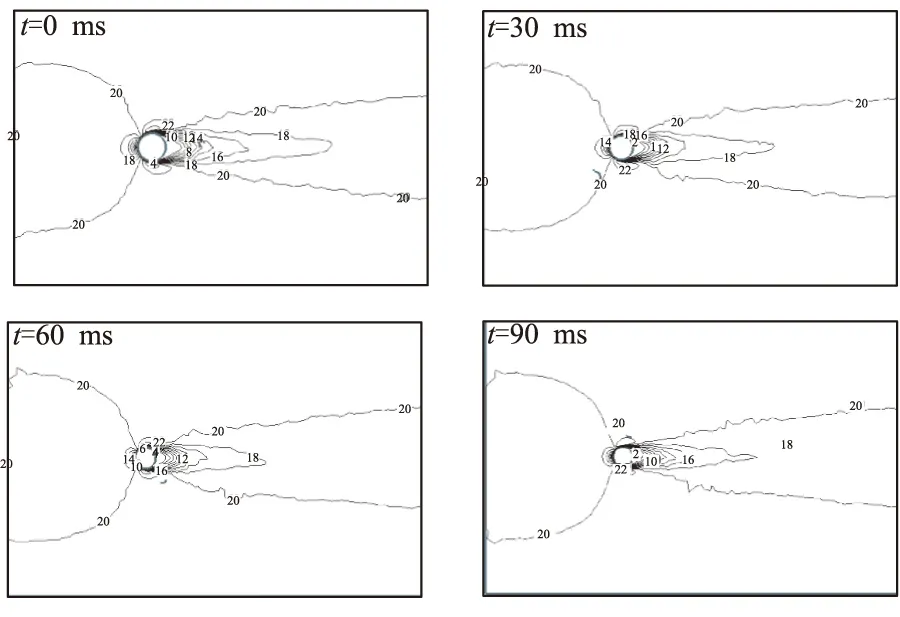
(a)当量直径颗粒

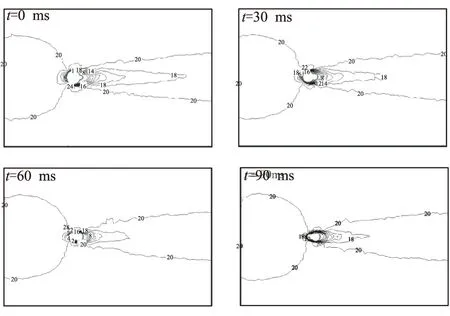
(b)真实颗粒

对比图3、图4中当量直径颗粒流场与真实颗粒流场流动情况可知，当t=0 ms，颗粒刚刚开始燃烧时，真实颗粒轴向长度大于当量直径下的颗粒，颗粒背风域所形成的流动尾迹较长。但此后，因当量直径下颗粒背风域所引起的涡流较强，气流需要较长的路径来恢复原来的速度。所以，其余3种工况下，真实颗粒背风域所形成的流动尾迹相对较短。因为颗粒在相变过程中呈现出不规则的几何形体，真实颗粒表面附近的压力分布出现较大波动，尤其在t=60 ms和t=90 ms时，颗粒外形明显分成两个区域。因此，在颗粒的表面处存在两处压力为0的点，这与当量直径下颗粒表面处的压力分布有很大区别。

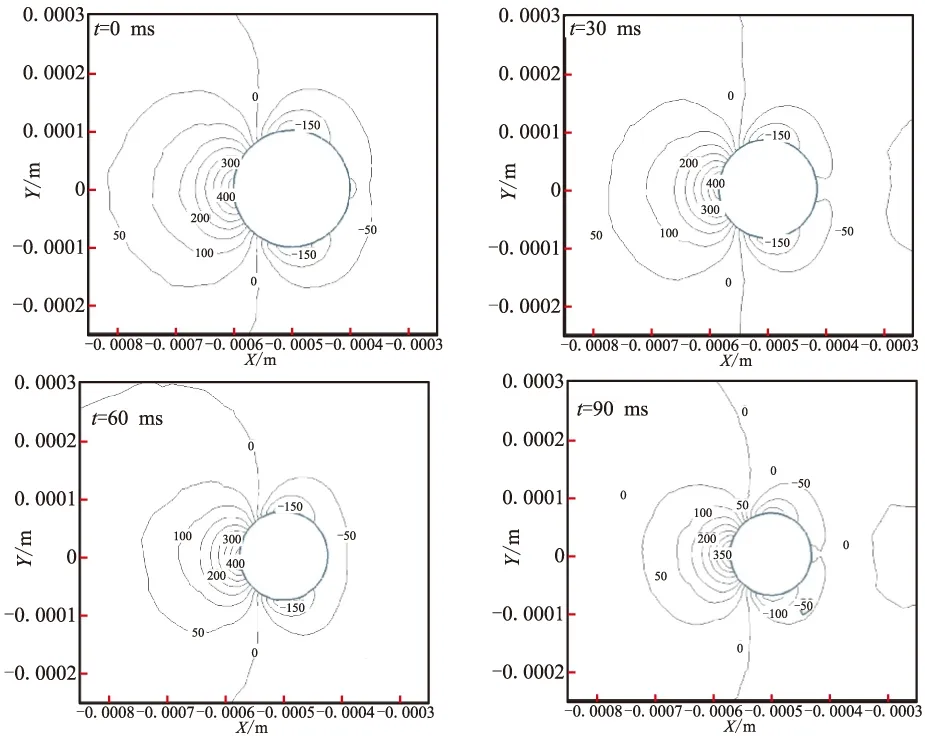
(a)当量直径颗粒

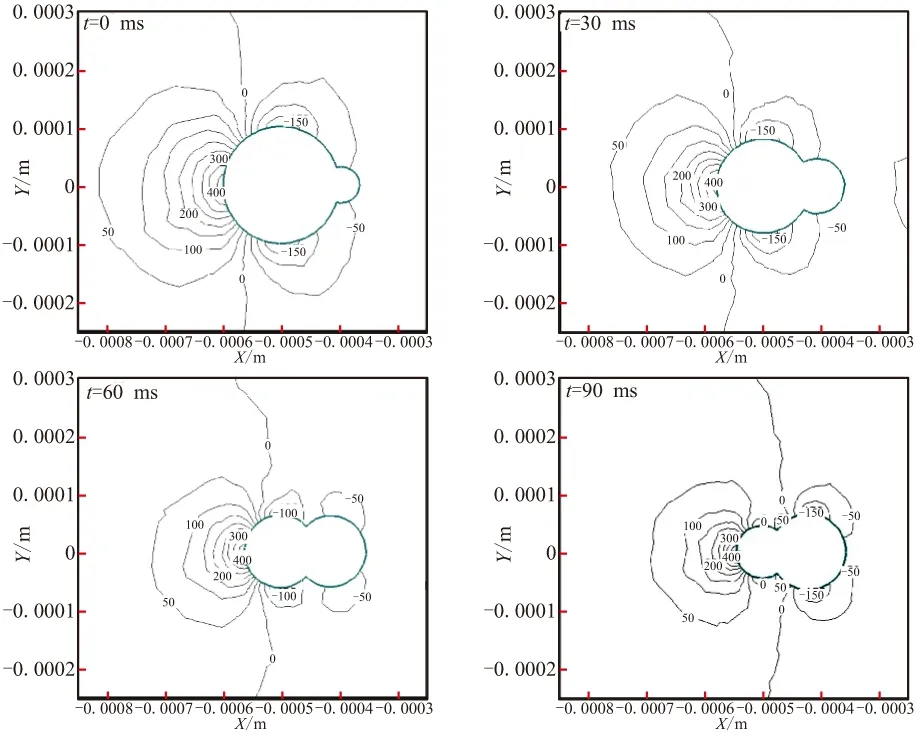
(b)真实颗粒

3.3 颗粒曳力对比分析

图5反映了铝颗粒在燃烧过程中其曳力系数的变化规律，以Cd表示；同时，也计算了当量直径下颗粒曳力系数变化，以Cdeq表示。由理论分析知，随着燃烧的进行，颗粒直径越来越小，将导致颗粒雷诺数不断降低，由此也会使得曳力系数不断升高。应用当量直径计算所得的结果也符合这一规律，但以真实颗粒计算时，二者却存在一定差别，整体而言，真实颗粒的曳力系数普遍大于当量直径下的颗粒。图5(a)表明，随颗粒相变燃烧的进行，真实颗粒表面的压力曳力系数发生很大变化，且无规律可循。因为颗粒的形状在燃烧过程中不断发生不规则的改变，所以其表面压力分布状况也表现出很大的波动。图5(b)表明，真实颗粒表面的粘性曳力系数一直大于当量直径下的颗粒，尤其当燃烧进行了60 ms后，以当量直径计算所得到的粘性曳力系数仅为真实颗粒的68.9%，当颗粒终止燃烧时，前者仍比后者高18%。图5(c)为颗粒的总曳力系数对比，其变化趋势与图5(b)相似。

从所计算的4种工况而言，以当量直径计算所得的压力曳力系数略高于真实颗粒，而粘性曳力系数则低于真实颗粒。所以，总曳力系数的偏差并不明显。但在颗粒燃烧进行到60 ms时，因外形已严重偏离球体，颗粒表面压力曳力系数与粘性曳力系数均大于当量直径下的计算值，其总曳力系数与经验公式计算所得的结果大不相同。此时，标准阻力曲线已不再适用，需对其进行相应的修正。

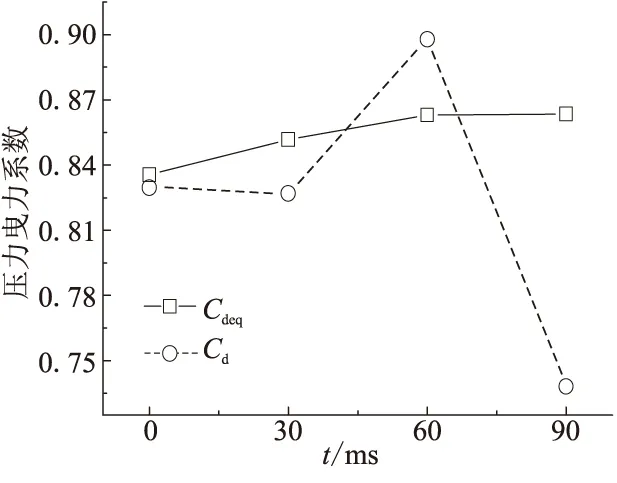
(a)压力曳力系数对比

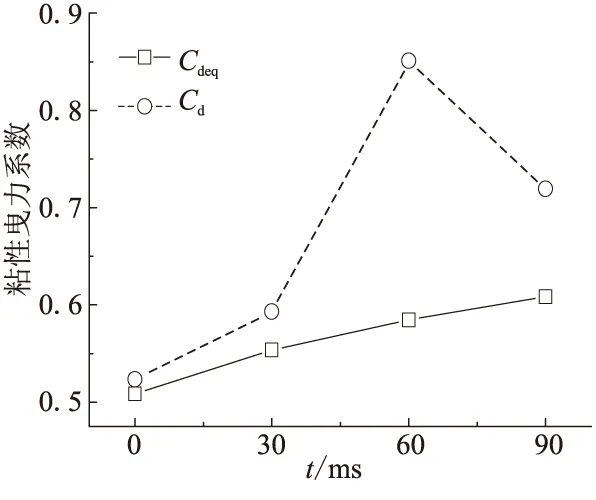
(b)粘性曳力系数对比

(c)总曳力系数对比

4 结论

因为金属颗粒在相变过程中呈现出不规则的几何形体，真实颗粒表面附近的压力分布与周围流场速度分布同球形颗粒有较大区别，其曳力系数亦有较大的变化。

(1)随着颗粒在流场中相变燃烧的进行，当颗粒尺寸减小时，颗粒背风域所形成的流动尾迹随之变短；同时，颗粒附近的压力变化区半径减小。

(2)在真实非球体颗粒的表面处，可能存在两处压力为0的点。颗粒直径的减小将导致其雷诺数降低，曳力系数不断升高。整体而言，真实颗粒的曳力系数普遍大于其当量直径颗粒。其中，压力曳力系数变化很大，但无规律可循。

(3)粘性曳力系数普遍大于当量直径下的颗粒，当燃烧进行60 ms后，其值为以当量直径计算所得结果的1.46倍。当颗粒终止燃烧时，前者仍比后者高出18%。

(4)当颗粒外形严重偏离球体时，经验公式计算所得的阻力系数有失精准。此时，标准阻力曲线已不再适用，可考虑对当量直径的计算结果进行系数修正。

[1] 方丁酉.两相流体力学[D].长沙:国防科技大学出版社，1988:55-58.

[2] Olsen S E,Beckstead M W.Burn time measurements of single aluminum particles in steam and CO2mixtures[J].Journal of Propulsion and Power,1996,12(4):662-671.

[3] 林建中.超常颗粒多相流体动力学——圆柱状颗粒两相流[M].北京:科学出版社,2008:85-86.

[4] Khan A R,Richardson J F.The resistance to motion of a solid sphere in a fluid[J].Chem.Eng.Commun,1987,62:135-150.

[5] Hartman M,Yates J G.Free-fall of solid particles through fluids[J].Collet.Czechoslov.Chem.Commun,1993,58(5):961-982.

[6] Komar P D.Settling velocities of circular cylinders at low Reynolds number[J].J.Geol.,1980,48:327-328.

[7] Loth E.Drag of non-spherical solid particles of regular and irregular shape[J].Powder Technology,2008,182:342-353.

[8] Sabine Tran-cng,Michael Gay,efastathios E Michaelides.Drag coefficients of irregular shaped particles[J].Powder Technology,2004,139:21-32.

[9] Youngho Suh,Changhoon Lee.A numerical method for the calculation of drag and lift of a deformable droplet in shear flow[J].Journal of Computational Physics,2013,241:35-57.

[10] Lu Hui-lin,Liu Wen-tie,Zhao Guang-bo.Computational modeling of dense gas particle flow in a pipe:kinetic theory approach of granular flow[J].Journal of Chemical Industry and Engineering (China),2005,5(1):31-38.

[11] Gan Lin,Xu Mao-sheng,zhu Bing-chen.Heat transfer parameters of packed bed with ring pellet[J].Journal of Chemical Industry and Engineering (China),2000,5(6):778-783.

[12] Robert Geisler.A global view of the use of aluminum fuel in solid rocket motors[R].AIAA 2002-3748.

[13] Merrill K King.Aluminum combustion in a solid rocket motor environment[J].Proceedings of The Combustion Institute,2009,32(2):2107-2114.

[14] Ounis H,Ahmadi G,McLaughlin J B.Brownian diffusion of submicrometer particles in the viscous sublayer[J].Journal of Colloid and Interface Science,1991,143(1):266-277.

[15] Unnikrisham A,Chhabra R P.An experimental study of motion of cylinders in Newtonian fluids:wall effects and drag coefficient[J].Can.J.Chem.Eng.,1991,9(9):729-735.

[16] Warnica W D,Renksizbulut M,Strong A B.Drag coefficients of spherical liquid droplets,Part 2:Turbulent gaseous fields[J].Experiments in Fluids.,1995,18:265-276.

[17] By Prosenjit Bagchi,Balachandar S.Inertial and viscous forces on a rigid sphere in straining flows at moderate Reynolds numbers[J].J.Fluid Mech.,2003,481:105-148.

(编辑：崔贤彬)

Numerical study on the change of surface drag force during metal particle combustion

HE Zheng，LIU Cong-lin，LI Zhuo，GU Xuan，GAO Ye
(College of Aerospace and Civil Engineering, Heilongjiang, Harbin 150001, China)

To study the force acted on the non-spherical particle which is produced by burning metal particle in solid ramjet motor,numerical simulation was employed to compare and analyze the drag of aluminum particle whose initial radius is 100 μm in variable phases of the burning process. Before that,the best computational model was determined and validated by comparing with the reference and experimental data.The results show that,in multiphase flow there are two points where the pressure is zero at the non-spherical particle's surface.Compared to the equivalent diameter particle, the real particle's drag coefficient is generally bigger.If the particle is not close to the spherical any more, the drag coefficient computed by the empirical formula is of great roughness,and the formula should be consequentially amended.

metal particle;non-spherical particle;combustion;equivalent diameter;drag coefficient

2014-07-04；

：2014-08-24。

国家自然科学基金(11372079)；中央高校基本科研业务费专项基金(HEUCF130203)。

贺征(1978—)，男，博士/副教授，研究方向为发动机内燃烧与多相流动。E-mail:hezheng1978@163.com

刘丛林(1981—)，女，博士。E-mail:383523445@qq.com

V435

A

1006-2793(2015)04-0492-05

10.7673/j.issn.1006-2793.2015.04.008