高超声速飞行器操纵性/控制律一体化设计方法

尉建利，王 聪，葛颖琛，闫 杰

(西北工业大学 航天学院，西安 710072)



高超声速飞行器操纵性/控制律一体化设计方法

尉建利，王 聪，葛颖琛，闫 杰

(西北工业大学 航天学院，西安 710072)

高超声速飞行器主要飞行阶段包括助推分离段、巡航段和下降段，在分离段操纵面的任务是快速抑制分离扰动，而巡航段主要用于高精度姿态控制。针对分离段和巡航段对舵面操纵性要求差别较大的特点，本文探讨从满足控制要求的角度对操纵面尺寸进行优化设计的方法，即操纵性/控制律一体化设计。采用最优控制方法对飞行器自动驾驶仪增益进行优化，并基于多目标遗传算法的并行子空间优化方法，得到了高超声速飞行器最优舵面外形尺寸和相应的控制律。仿真结果表明，最优舵面在分离段能够快速抑制分离扰动对飞行器姿态的影响，并将飞行器姿态迅速调整到发动机点火窗口；在巡航段能够快速抑制阵风干扰对飞行器姿态的影响，稳定飞行器姿态，为高超声速飞行器操纵性设计提供了依据。

高超声速飞行器；操纵性; 控制律;一体化设计

0 引言

高超声速飞行器是指飞行速度在5倍声速以上，在大气层或跨大气层实现高速远程飞行的飞行器，其典型特征是使用超燃冲压发动机。超燃冲压发动机对点火和工作条件的要求相当苛刻，由于其需要在较高的马赫数和一定的动压条件下才能点燃，因此目前的高超声速巡航飞行器均使用助推器。高超声速飞行器由于要抑制分离扰动，并使飞行器快速达到冲压发动机工作要求的姿态，通常使用有较高操纵效率的全动舵面；而在巡航段，飞行器控制的首要目的是保证超燃冲压发动机工作所需的最优姿态条件，大约是平衡攻角±2°，侧滑角±2°，否则发动机将熄火，且飞行器姿态越接近设计值，燃料燃烧越充分，发动机工作性能越好，因此在巡航段需要进行高精度姿态控制。由于这两个阶段对操纵性的需求差别较大，这就需要找到最优操纵性的设计方法，使其能对飞行器各阶段的控制效果达到最优，为此本文提出了高超声速飞行器操纵性/控制律一体化设计的方法。

操纵性/控制律一体化设计方法在常规飞行器设计中已进行了部分研究，目前主要有2种方法进行解决：一是采用多学科设计优化(MDO)的方法[1]，主要有并行子空间(CSSO)，协同优化(CO)，单学科可行法(IDF)，多学科可行法(MDF)，两级系统集成综合(BLISS)等方法；二是考虑飞行器飞行条件和各种约束条件的工程方法。Kevin M Ryan[2]利用鲁棒多目标遗传优化方法对飞行器设计优化，研究了操纵性在飞行器设计中的影响，并与多目标优化方法和聚类方法进行比较分析。张勇[3]提出了一套面向控制的一体化设计方案，以飞行器控制性能为优化目标，对气动、推进、结构控制等参数进行一体化综合优选来设计高超声速飞行器，论文中对气动的考虑主要在飞行器的构型和外形参数，而对操纵性与控制的优化设计未涉及。张登峰[4]采用响应面方法对无尾无人机操纵面的气动效益和控制进行建模，采用多目标遗传算法得到优化解集，利用模糊决策技术选取最终解。Sadraey M[5]采用系统工程方法，估计无人机在临界飞行条件下的操纵力需求，并分析了操稳特性，从而对无人机操纵面进行设计。Ruben E Perez[6]采用改进协同优化方法，在飞行器概念性设计过程中对动力和控制系统一体化设计，并对各子学科进行分析和建模。Catherine Bahm和Ethan Baumann[7]分析了X-43A飞行器的导航制导与控制方法以及其飞行试验的结果，重点分析了飞行器在分离过程中采用攻角自动驾驶仪的控制逻辑，以及在巡航段和下降段的姿态驾驶仪和过载驾驶仪之间的切换方法，并利用Monte Carlo方法对整个飞行器的飞行过程作仿真分析。Davidson J,Lallman F[8]介绍了美国Hyper-X计划试飞成功的X-43A飞行器整个飞行过程，并给出任务飞行器在超燃冲压发动机试验阶段和下降段的控制律框图，分析该控制回路的控制性能和鲁棒特性。目前关于高超声速飞行器操纵性/控制一体化设计的文献未见报道。

本文提出了以控制性能最优为目标的高超声速飞行器操纵性/控制律一体化设计优化方法，论文采用并行子空间的优化方法，通过建立基于径向基神经网络的气动学科和控制学科的响应面模型，来近似状态变量与设计变量之间的关系，在满足子空间和系统级约束的前提下，逐步迭代至收敛，并得到最优的舵面参数及其与之匹配的控制系统。

1 优化设计方法

多学科设计优化方法是一种针对复杂系统进行设计和优化的策略，它将复杂的大系统分解成多个易于处理的子系统，但各子系统之间存在相互耦合变量。并行子空间方法[9]可用来解决多学科设计中的多目标问题，它的每一次优化均包含系统分析和敏感性分析，并能够在具有强耦合特性的MDO问题中找出系统的Pareto解集。

图1是一个具有2个目标和2个相互耦合系统的MDO问题。其中XA和XB代表2个子系统的设计量，YA和YB代表了2个子系统之间相互耦合的变量，FA和FB分别代表2个子系统的优化目标。在并行子空间方法中，并没有系统级的优化目标函数，而是利用每个子空间中独立的目标函数作为优化目标，在每个循环周期中对2个子空间并行优化直至收敛。

图1 MDO问题示意图Fig.1 MDO problem frame

为克服系统分析十分耗时的缺陷，可采用响应面方法对子系统进行近似，在优化过程中通过响应面模型获取子系统需要的状态变量和耦合变量的信息。式(1)是两目标并行子空间优化问题:

(1)

式中F为目标函数；X为设计向量；Y为耦合向量；C为不等式约束；H为等式约束；RSM表示响应面模型。

本文主要考虑高超声速飞行器舵面几何参数的不同对操纵性和控制律带来的影响，以及气动学科与控制学科间的耦合关系，对操纵性和控制律一体化设计。一方面，气动计算得出的气动力和力矩系数会对控制学科的计算和设计造成影响；另一方面，舵面的偏转指令由控制系统给出，并将引起飞行器气动力和力矩系数的变化。

针对高超声速飞行器操纵性和控制性能之间的相互影响关系，本文分别建立了气动学科和控制学科模型，作为系统优化的2个子空间，并以气动力和力矩系数作为2个子空间之间的耦合变量，对飞行器的操纵性和控制律进行一体化设计。

2 高超声速飞行器气动模型

本文设计的高超声速飞行器气动外形与美国海军研究办公室2002年启动的HyFly计划中的飞行器类似，是一种轴对称飞行器。飞行器包括助推器和任务飞行器两部分，任务飞行器采用锥形头部，圆柱形弹体的结构，肩部安装进气道与超燃冲压发动机相连，弹体尾部安装操纵舵面，如图2所示。高超声速飞行器舵面尺寸如图3所示。共有舵面梢部位置(X2)、根部弦长(C1)、梢部弦长(C2)、梢部到轴线距离(S2)4个因素，每个因素各取4个水平作为正交试验设计的数据，表1为因素水平表。

图2 高超声速任务飞行器Fig.2 Hypersonic vehicle

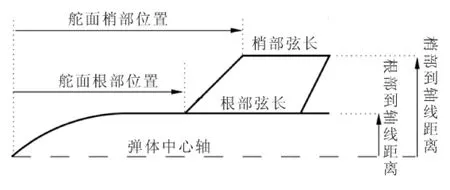
图3 舵面参数示意图Fig.3 Rudder surface parameters

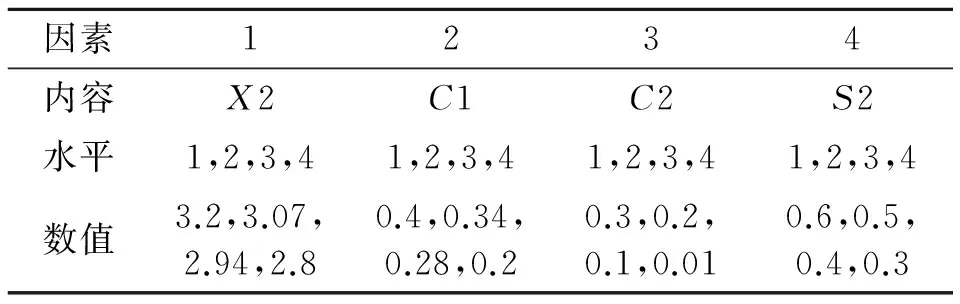
表1 正交试验设计因素水平Table1 Levels of orthogonal test factor m

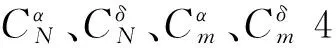
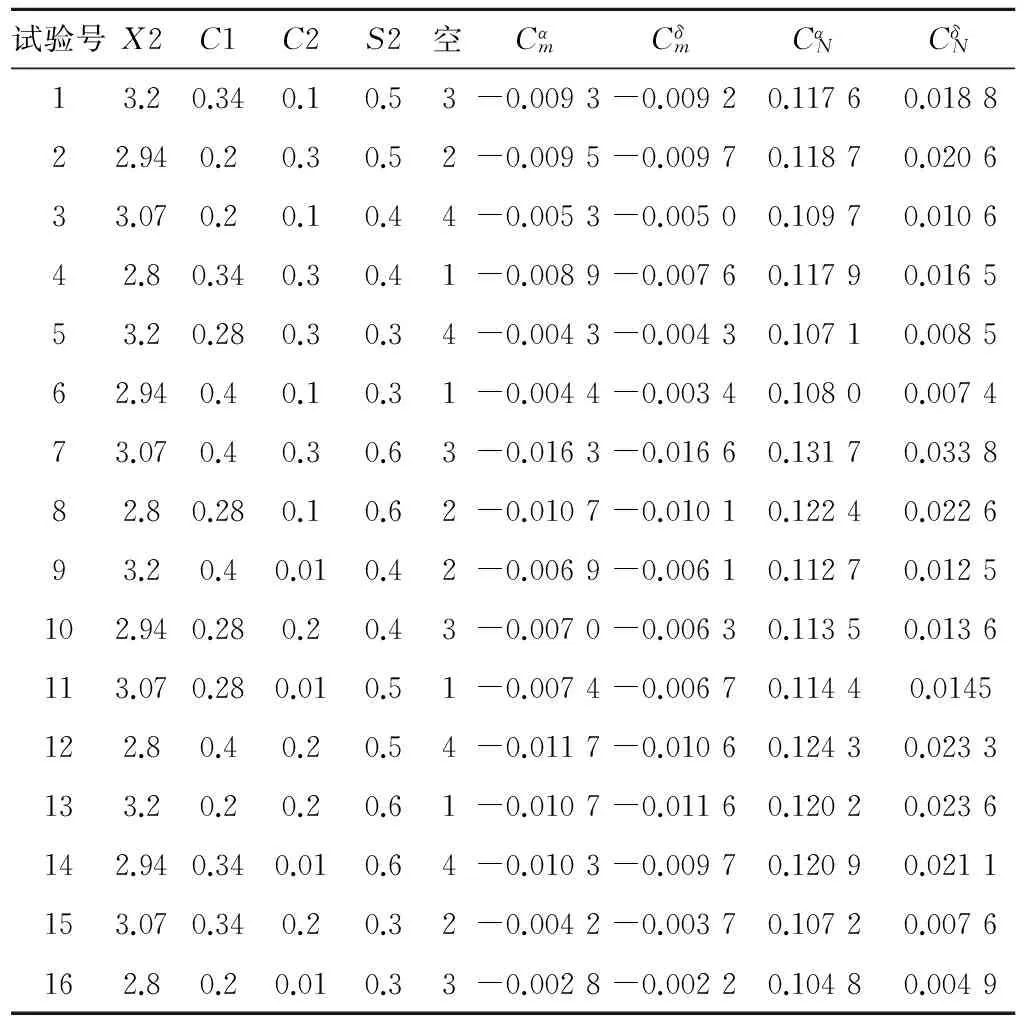
表2 正交试验表Table2 Orthogonal test table

气动学科的响应面模型为气动系数的偏导数与全动舵面几何参数的函数关系，具体数值选取如表2所示，在马赫数一定的前提下，响应面模型可表示为式(2)的形式：

(2)

3 高超声速飞行器控制系统模型

本文的高超声速飞行器是轴对称外形，其纵向和侧向特性相同，因此仅以俯仰通道为例进行控制系统设计。其中分离段要求任务飞行器能够快速克服分离扰动的影响，达到超燃冲压发动机要求的开机窗口；巡航段要求飞行器能够克服飞行环境中的扰动影响，使姿态角和姿态角速度始终保持在发动机的工作条件范围内。在这两个飞行阶段，要求自动驾驶仪能够对高超声速飞行器精确姿态控制，本文采用如图4所示的攻角驾驶仪，并研究了基于LQR的攻角驾驶仪最优控制设计问题[10]。

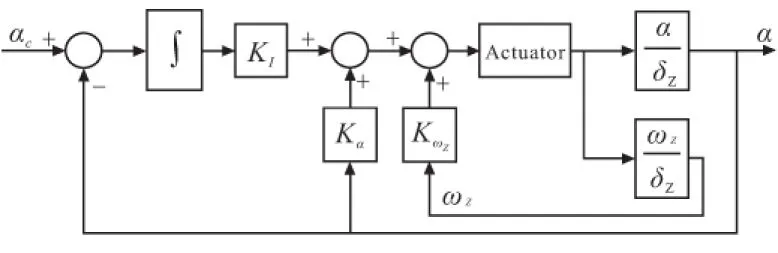
图4 攻角驾驶仪框图Fig.4 Angle of attack autopilot

本文采用LQR方法计算驾驶仪中的增益控制器。飞行器的纵向运动可以用飞行器的短周期运动方程近似描述，纵向运动的小扰动线性化模型如式(3)所示：

(3)

其状态空间描述为

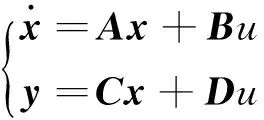
(4)

其中，

图4中的被控对象传递函数如式(5)和式(6)所示:

(5)

(6)

根据LQR最优控制问题中的跟踪调节器问题[11]对本文中采用的纵向自动驾驶仪结构进行设计，最优性能指标定义为攻角跟踪的误差、俯仰角速率以及舵偏角速率的加权平方和的形式，其中，攻角跟踪误差和俯仰角速率为观测量，舵偏角速率为输入量，其惩罚函数为

(7)

其中，

将跟踪问题转化为标准LQR问题，令

x2=C1x1，y2=x2，u2=u1

(8)

则状态方程可转化为

(9)

惩罚函数中对应的加权系数可转化为

(10)

根据标准LQR问题的求解方法，求解式(11)的代数Riccati方程：

(11)

则控制系统的增益为

(12)

最优控制指令为

u2=Kx2=K(y1-D1u1)

(13)

即

(14)

因此该驾驶仪结构的最优控制指令可表示为

(15)

利用正交试验设计方法选取的16个全动舵面设计点，飞行条件均为高度22 km，飞行速度Ma=6，攻角5°。计算16个设计点的静稳定动力系数a24、操纵动力系数a25、法向力动力系数a34和舵面动力系数a35作为响应面模型的输入变量，以最优控制性能指标J和控制系统调节时间ts为目标，采用径向基神经网络方法构建高超声速飞行器控制学科的响应面近似模型，并选择高斯函数作为该网络的径向基函数。则响应面模型如式(16)所示:

(16)

4 优化算法及优化结果

本文优化算法选用多目标遗传算法(MOGA)对系统优化设计[12]。MOGA是一种处理大规模问题时，搜索Pareto最优解的算法。该算法利用GA中适应值函数的概念，配合选择、交叉、变异等算子进化种群，在每一次迭代时，均能进化生成一组新的解，同时引入多目标优化算法中非劣解的概念，并且使用小生境技术来提高种群的多样性。本文优化设计的任务是在满足约束条件下，找到控制性能最优的舵面参数并得到相应的控制系统，即通过优化式(17)所述的问题得到最优解：

minY=[J,ts]

(17)

整个设计优化的流程主要分4步对系统进行寻优：

(1)确定优化问题的数学模型，即将高超声速飞行器的气动学科响应面模型和控制学科响应面模型加入到优化过程中。

(2)求解式(17)，利用MOGA算法对设计变量进行寻优，得到Pareto最优解集。优化过程中采用步骤1中所获得的响应面模型进行计算分析，因为控制学科响应面模型已隐含了控制系统的作用，不需要对每个子代个体设计准确的控制器。

(3)根据优化所得到的Pareto非劣解集，通过CFD软件计算Pareto前沿上不同舵面参数对应的高超声速飞行器在相同飞行条件下的气动数据，分析飞行器的气动数据和操稳特性。再根据LQR最优控制系统设计方法对最优解设计相应的控制系统，并在时域和频域下分析控制系统的性能指标。

minY=[J,ts]

(18)

(4)对所得最优解在分离段和巡航段分别作纵向三自由度的仿真分析，观察该飞行器在相应自动驾驶仪的控制下，对姿态角指令的跟随情况，以及在加入扰动后飞行器姿态角和角速度的响应情况。

根据分离段对高超声速飞行器操纵性要求，优化分离过程中使用的全动舵面，其优化问题为求解式(18)，利用MOGA算法对设计变量进行寻优，设置种群大小为50，最大进化代数为100，停止代数也为100，Pareto最优解个数为15。优化所得的Pareto最优解对应的状态变量如表3所示。

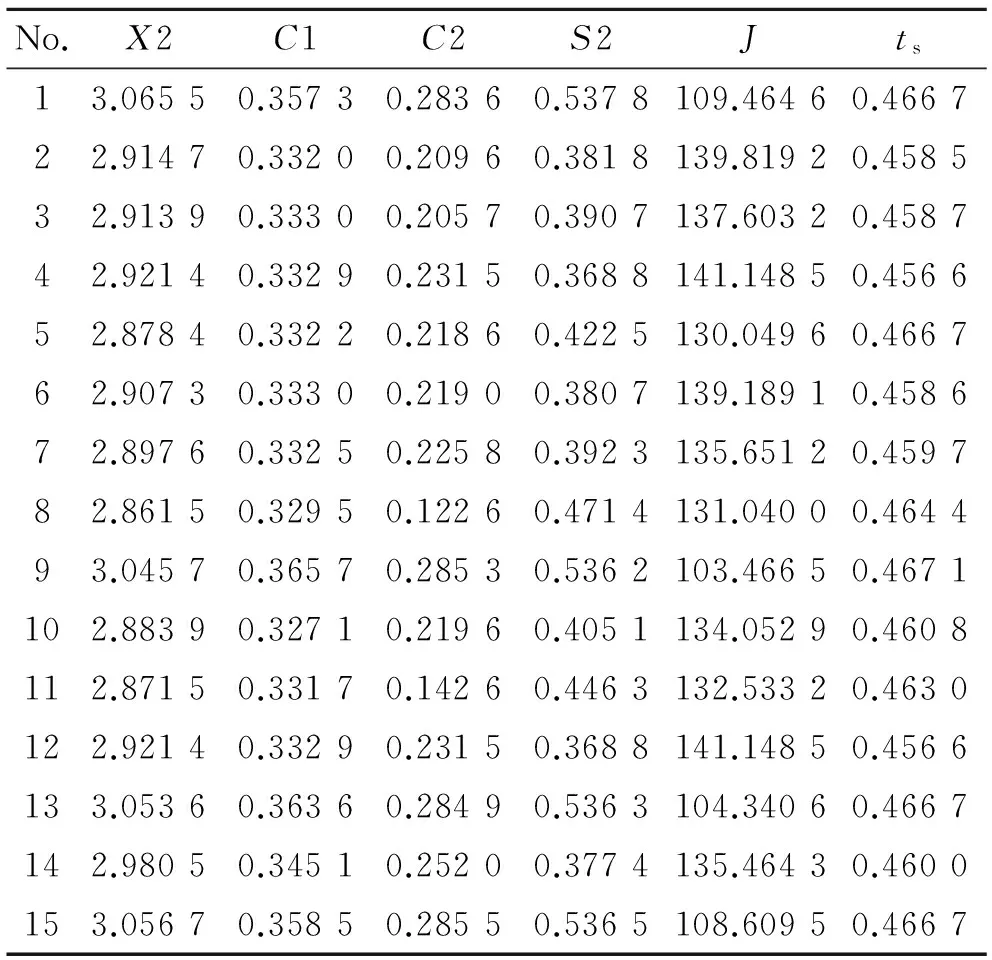
表3 全动舵面Pareto最优解Table3 Pareto optimal solutions for control surface

因为调节时间相差很小，故选择最优性能指标J最小值的对应项为优化所得的系统最优解，即第9组参数。

采用第3节中的LQR最优控制问题求解方法，选取惩罚函数中的加权系数如下：

Q11=5，Q22=0.06，R11=0.001

可计算得到最优舵面下攻角自动驾驶仪各回路的增益，如式(19)所示:

(19)

则自动驾驶仪开环Bode图如图5所示，可知该攻角回路的幅值裕度为13.9dB，相角裕度为70.4°，满足10dB、60°的设计条件。

阶跃响应曲线如图6所示，可知系统调节时间约为0.5s，系统无稳态误差。

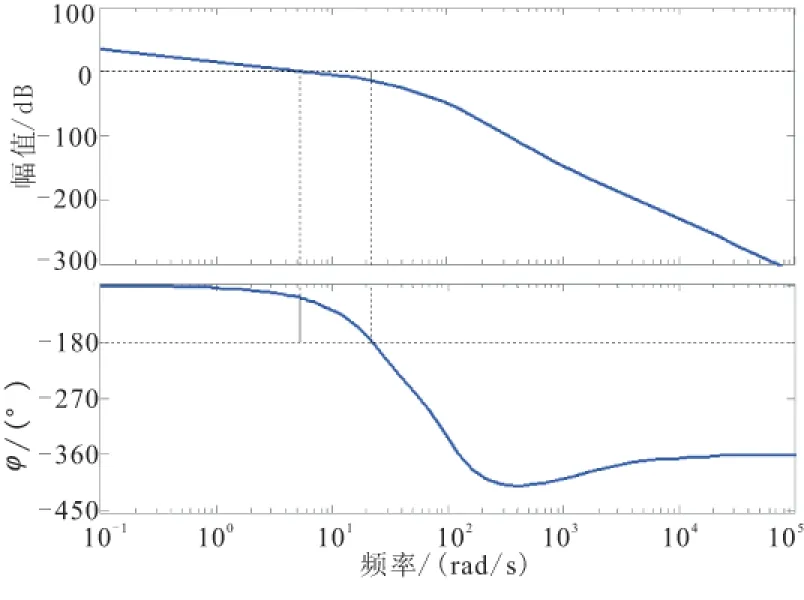
图5 攻角回路Bode图Fig.5 Bode plot for angle of attack loop

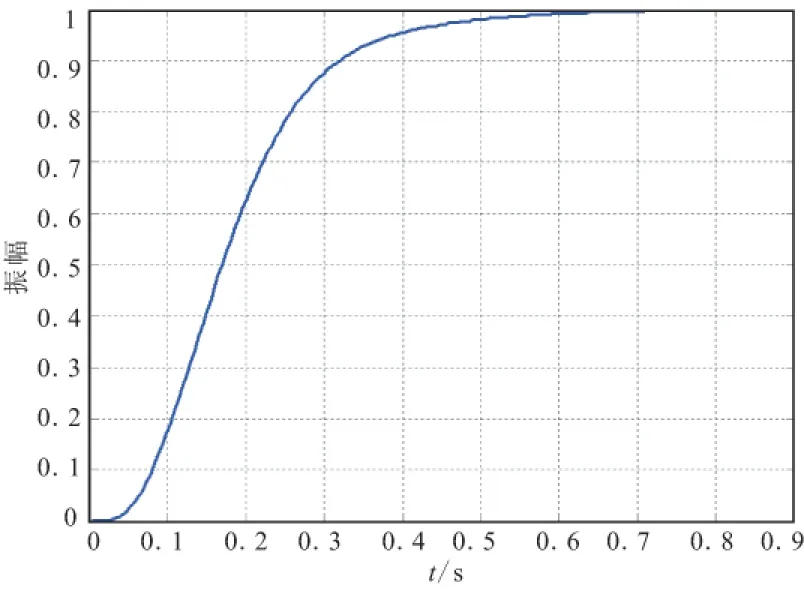
图6 驾驶仪单位阶跃响应曲线Fig.6 Unit step response for autopilot

5 仿真验证

5.1 分离段纵向模型仿真分析

本文讨论的高超声速飞行器的分离高度为22 km，分离时刻速度约为Ma=6，飞行器超燃冲压发动机点火的攻角为4.8°。在分离时刻(2 s)加入分离扰动模型，其中俯仰角速度最大15 (°)/s，攻角最大值为2°。

选取正交试验表2中的16种舵面尺寸及相应的控制器参数的仿真结果与最优舵面条件下飞行器的仿真结果进行对比，飞行器在分离过程中的攻角和舵偏角曲线，分别如图7和图8所示。

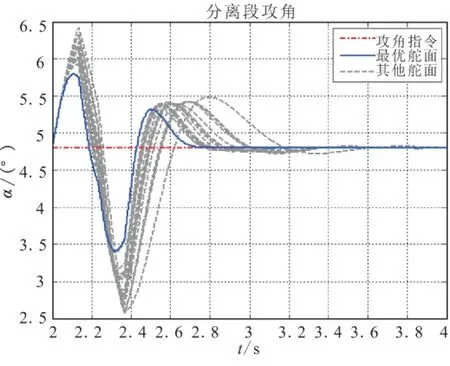
图7 分离段攻角对比Fig.7 Angle of attack in separation part

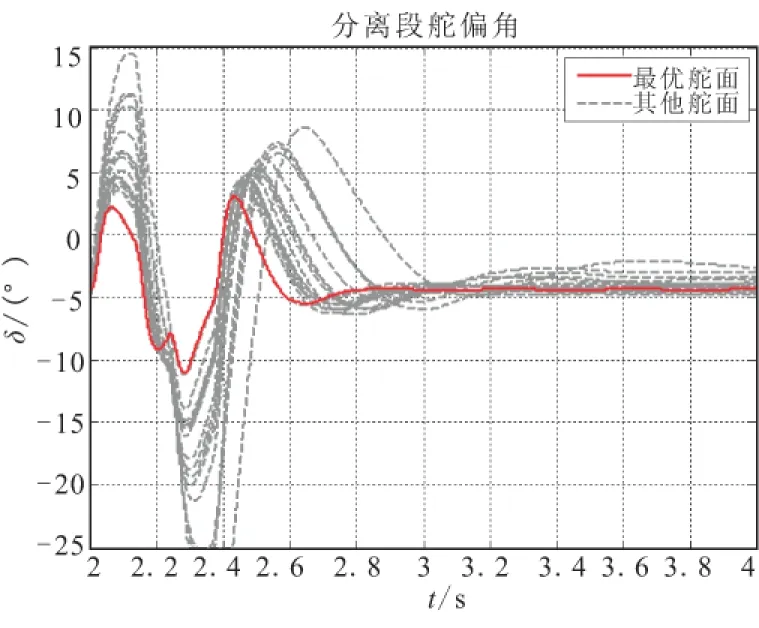
图8 分离段舵偏角对比Fig.8 Deflection in separation part

由图7可知，飞行器为克服分离扰动带来的影响，将姿态从初始分离时刻调整到超燃冲压发动机的开机条件4.8°攻角。首先，在最优舵面条件下，飞行器攻角的最大抖动幅值约为1.5°，调节时间在1 s以内，在姿态调节的最后阶段，最优舵面能很准确的达到攻角指令。其次，从图7中可知，最优舵面的对扰动的抑制能力要优于其他舵面的情况，具有更小的姿态角抖动幅值和更快的姿态调节时间。

由图8可知，在最优舵面条件下，飞行器的舵偏角在+3°～-10°范围内变化，而其它舵面偏转角度较大，会导致飞行器舵面面临的铰链力矩值较大，容易对舵机造成冲击，同时会导致飞行器进入非线性区域。

5.2 巡航段纵向模型仿真分析

飞行器巡航高度约为22 km，巡航马赫数约为Ma=6，巡航段的平衡攻角为4.8°。在巡航段加入阵风扰动模型。飞行器在巡航段受到扰动后，姿态角变化幅值较小，故此时需要考虑舵机死区和间隙带来的影响，认为其值为0.3°。

分2种情况仿真，首先在第10 s加入NASA复合型9 m/s阵风扰动，对比飞行器对大幅值风干扰的抑制能力；其次加入幅值为4 m/s的连续正弦形阵风，对比飞行器对小幅值持续风干扰的抑制能力，仿真结果如图9～图11所示。

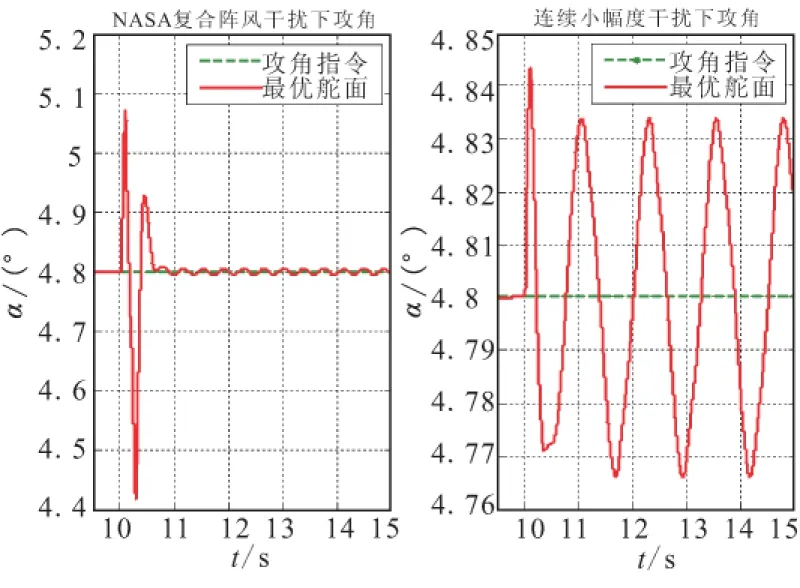
图9 巡航段攻角Fig.9 Angle of attack in cruise part

由图9可知，当在巡航段飞行过程中出现强阵风干扰时，采用最优舵面抑制扰动，其控制快速性约为0.6 s。飞行器攻角变化的幅值为0.3°。阵风过后，最优舵面控制的飞行器由于舵机间隙和死区的影响，姿态会在小幅度范围内抖动。当出现幅值较小的持续扰动时，最优舵面具有很好的扰动抑制能力，飞行器姿态的抖动幅值在0.1°以内。

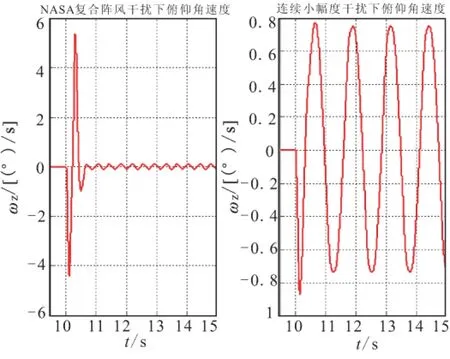
图10 巡航段俯仰角速度Fig.10 pitch rate in cruise part

由图10可知，强阵风干扰下，采用最优舵面的高超声速飞行器，俯仰角速度变化幅值约为3 (°)/s。在小幅度持续干扰条件下，采用最优舵面能够将飞行过程中飞行器姿态的抖动角速度保持约为0.8 (°)/s。

由图11可知，采用最优舵面时，飞行器舵偏角的变化在2.5°范围内。由于间隙的影响，会产生振荡并影响飞行器的姿态出现抖动现象。在小幅度持续干扰下，最优舵面对扰动很敏感，能够迅速的对扰动做出响应。

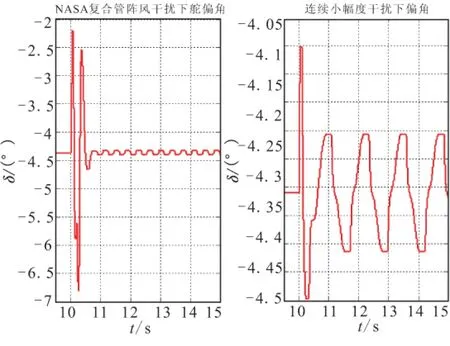
图11 巡航段舵偏角Fig.11 Deflection in cruise part

6 结论

(1)为满足高超声速飞行器在分离段和巡航段操纵性需求差别比较大的要求，本文提出了基于响应面的并行子空间优化策略对高超声速飞行器操纵性/控制律一体化设计方法。

(2)设计了基于LQR控制器改进的攻角驾驶仪，在保证时域、频域具有良好特性的同时，对分离段和巡航段均具有较好的抗干扰能力。

(3)通过仿真验证可知，本文提出的操纵性/控制律一体化设计方法，能够设计出优于其他舵面外形的最优解，有效提升高超声速飞行器在分离段稳定姿态的快速性，且有效抑制巡航段大气扰动的影响，具有较高的控制精度，为高超声速飞行器高精度控制提供了新的思路。

[1] Jaroslaw Sobieszczanski-Sobieski.Multidisciplinary aerospace design optimization:survey of recent developments[C]//34th Aerospace Sciences Meeting and Exhibit,January 1996.

[2] Kevin M Ryan,Mark J Lewis.Comparison of robust optimization methods applied to hypersonic vehicle design[C]//Guidance,Navigation,and Control and Co-located Conferences,19-22 August 2013,Boston,MA,AIAA 2013-4680.

[3] 张勇,陆宇平.高超声速飞行器控制一体化设计[J].航空动力学报,2012,27(12):2724-2732.

[4] 张登峰,高金源.基于MDO技术的飞机操纵面参数/飞行控制律多目标优化设计[J].航空学报,2008,29(6): 1626-1633.

[5] Sadraey M,Colgren R.A systems engineering approach to the design of control surfaces for UAVs[C]//45th AIAA Aerospace Sciences Meeting and Exhibit,8-11 January 2007,Reno,Nevada,AIAA 2007-660.

[6] Ruben E Perez,Hugh H T Liu.Flight dynamics and control multidisciplinary integration in aircraft conceptual design optimization[C]//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference,30 August-1 September 2004,Albany,New York,AIAA 2004-4435.

[7] Catherine Bahm,Ethan Baumann,John Martin.The X-43A Hyper-X Mach 7 flight 2 guidance,navigation,and control overview and flight test results[R].AIAA 2005-3275.

[8] Davidson J,Lallman F,McMinn J D.Flight control laws for NASA's Hyper-X research vehicle[R].AIAA-99-4124.

[9] Huang C H,Galuski J.Multi-objective pareto concurrent subspace optimization for multidisciplinary design[J].AIAA Journal,2007,45(8).

[10] Curtis P Mracek,Brett Ridgely D.Missile longitudinal autopilots:connections between optimal control and classical topologies[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,AIAA 2005-6381.

[11] Curtis P Mracek,Brett Ridgely D.Optimal control solution for dual(tail and canard)controlled missiles[C]// AIAA Guidance,Navigation,and Control Conference and Exhibit,AIAA 2006-6569.

[12] Parashar S,Bloebaum C L.Multi-objective genetic algorithm concurrent subspace optimization(MOGACSSO)for multidisciplinary design[R].AIAA 2006-2047.

(编辑：吕耀辉)

Integrated design method for manipulability and control law of hypersonic vehicle

WEI Jian-li,WANG Cong,GE Ying-chen,YAN Jie

(College of Astronautics,Northwestern Polytechnical University,Xi'an 710072,China)

The main flight phases of a hypersonic vehicle include propulsion-assisted separation phase,cruise phase and descent phase.In the separation phase,the task of control surface is to suppress the separation perturbation of the hypersonic vehicle quickly,but in the cruise phase,the task is to achieve the high-precision control of its attitude.During these two phases,the requirements for the manipulability of the rudder surface are rather different.To satisfy the control requirements,this paper explores the control surface dimension optimization and design method,namely the manipulability and control law integrated design method. It uses the optimal control method to optimize the gains of the autopilot of the hypersonic vehicle and then optimizes the boundary dimensions of its optimal rudder surface and its control law with the parallel subspace optimization method of the multi-objective genetic algorithm. The simulation results show that,during the separation phase,he optimal rudder surface can quickly suppress the influence of separation perturbation on the attitude of the hypersonic vehicle and quickly adjust its attitude to the engine ignition window and that,during the cruise phase,the optimal rudder surface can quickly suppress the influence of gust interference on the attitude and thus stabilize it.This exploration sheds light on a hypersonic vehicle's manipulability design.

hypersonic vehicle;manipulability;control law;integrated design

2015-07-01；

：2015-07-23。

国家自然基金(91216104)。

尉建利(1978—)，男，博士，研究方向为高超声速飞行器控制。E-mail：weijianli@mail.nwpu.edu.cn

V221

A

1006-2793(2015)05-0601-07

10.7673/j.issn.1006-2793.2015.05.001