双向涡数值模拟雷诺应力各向异性研究与分析
党进锋,郜 冶,刘加宁
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
双向涡数值模拟雷诺应力各向异性研究与分析
党进锋,郜 冶,刘加宁
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
以实验数据和理论结果作为参考,探讨基于布茨涅克各向同性假设的RNGk-ε模型、SST模型和各向异性RSM湍流模型在双向涡流数值计算中的适用性,并对不同入射速度下的双向涡流结构进行了比较分析。计算结果表明,基于布茨涅克各向同性假设的RNG模型与SST模型在不同入射速度下均无法得到内部受迫涡、外部自由涡的双向涡流结构,而RSM模型则可以准确得到双向涡流结构。内、外涡分界面处雷诺正应力各向异性特征显著,且随入射速度的提高而增强,最大差值达到了198%,轴线附近流场雷诺正应力各向异性特征相对较弱,但是最大差值依然达到46%,因此基于布茨涅克各向同性假设的湍流模型不适用于涡流冷壁发动机数值模拟研究。
双向涡流;涡流冷壁发动机;雷诺应力;各向异性
0 引言
涡流是自然界中普遍存在的一种流动形式,大到天体星云的运动,小到湍流中的粘性耗散涡,均是不同形式的涡流。由于涡流具有丰富多样的结构形式,近年来被越来越多的应用在流体机械中,如涡流燃烧器、涡流固液组合发动机、涡流分离器等。2002年,美国Orbital科技公司Chiaverini等提出了一种新概念液体火箭发动机形式[1],氧化剂从发动机喷管上方沿切向喷入发动机内形成外部涡流,外部涡流向发动机顶端旋转流动,在发动机顶端改变流动方向,并与顶端喷入的燃料混合形成内部燃烧涡流,燃烧的内部涡流从喷管流出产生推力,该发动机被称为涡流冷壁发动机(Vortex Combustion Cold-Wall Chamber VCCWC)。VCCWC的优点在于氧化剂所形成的外部涡流对于发动机壁面起到了冷却作用,大大降低了发动机内壁热防护层厚度,核心流内氧化剂与燃料旋转燃烧,增加了反应时间从而缩短了反应距离,最终可减小发动机长度,该两方面优点均有助于降低发动机成本,因此美国NASA将VCCWC确定为未来廉价发动机的候选方案[2-3]。由于VCCWC内部涡与外部涡流动方向相反,因此该组合涡称为双向涡流(Bidirectional Vortex)。
从VCCWC中双向涡流问题的提出至今十余年时间里,有限研究工作主要分为两部分,一部分为Chiaverini等所做VCCWC冷流与燃烧实验[4],实验验证了双向涡流的存在并得到内涡旋转燃烧图像。另一部分为Majdalani等开展的双向涡流理论研究,文献[5]中推导得到不可压无粘流双向涡流结构解析式,文献[6]中推导得到不可压粘性核心双向涡流结构解析式,文献[7]得到定常剪切应力核心流模型,文献[8-9]中分别通过Bragg-Hawthorne流函数法和Beltramian流场近似法得到可压缩双向涡流模型。
与之相比,双向涡流CFD研究进展较慢。由于双向涡流三维效应显著,且涉及到VCCWC化学反应数值计算,计算量巨大,因此LES、DNS等方法的数值研究还未开展。Fang在文献[10]中结合Standardk-ε模型和RSM模型数值计算模拟了VCCWC冷流与燃烧过程,从其冷流计算结果来看速度曲线与理论曲线趋势相似,能够得到内、外双向涡流结构。文献[11]中通过数值计算指出外部涡流厚度约占发动机半径的25%~29%,并提出冷却剂喷嘴倾斜一定的角度可增强内部涡流强度、改善推进剂掺混程度提高燃烧效率。文献[12]中数值计算研究了以GH2/GO2为燃料的VCCWC燃烧过程。
文献[13]中通过二维物理模型比较了RNG 模型和RSM模型在VCCWC数值模拟中的准确性,指出RSM模型更适合于强旋流场。本文在文献[13]工作基础上,对VCCWC内流场进行了三维完整物理模型、3种不同湍流模型、3种不同入射速度下的数值计算研究,定量探究RSM模型更适合VCCWC数值计算的内在原因。计算发现双向涡流结构对于湍流模型的选择性非常大,不合适的湍流模型计算所得结果与实验结果差别非常明显,甚至可以说是完全错误的,分析原因认为:双向涡流与普通流动的区别在于,双向涡流在远离壁面的核心流区域内湍流脉动雷诺正应力各向异性特性依然异常显著,而基于布茨涅克各向同性假设(Boussinesq Isotropic Hypothesis)的湍流模型则认为核心流区域各向雷诺正应力均相等[14],这就导致了传统基于布茨涅克各向同性假设的湍流模型无法得到正确结果。
本文以文献[15]中实验数据及文献[5,16]中理论结果作为参考,探讨基于布茨涅克各向同性假设的RNGk-ε模型、SST模型和各向异性RSM湍流模型在双向涡流数值计算中的适用性,并对不同入射速度下的双向涡流结构进行了比较分析,结论可用于指导双向涡流数值模拟湍流模型的选择。
1 物理模型及数值计算方法
图1(a)、(b)分别为双向涡流物理模型示意图及入射喷口分配示意图。物理模型直径d=100 mm,长度L=100 mm,即长径比α=1,模型顶部为平面。入射喷口横截面为5 mm×4 mm矩形,模型底部12个入射喷口周向均匀排列,采用切向速度入口形式。本文中物理模型与文献[10,13]中类似,因此采用与文献[10,13]相同的Outflow出口边界条件,出口直径为30 mm,其余均为无滑移壁面。

(a)VCCWC物理模型 (b)入射喷口分配示意图
物理模型网格示意图如图2所示。计算中,3种湍流模型(RNGk-ε模型、SST模型及RSM模型)均采用SIMPLE算法求解,梯度差分采用G-S节点基格式,压力差分采用二阶格式,其余通量差分均为二阶迎风格式。Majdalani在文献[5]中指出双向涡流在不可压缩与可压缩流动中均存在,因此计算中采用低速不可压缩流形式,流体介质为理想不可压空气,3种入口速度分别为10、15、20 m/s。计算工作在64位服务器上完成,耗时320 h,所使用的CFD软件为ANSYS FLUENT11.0。
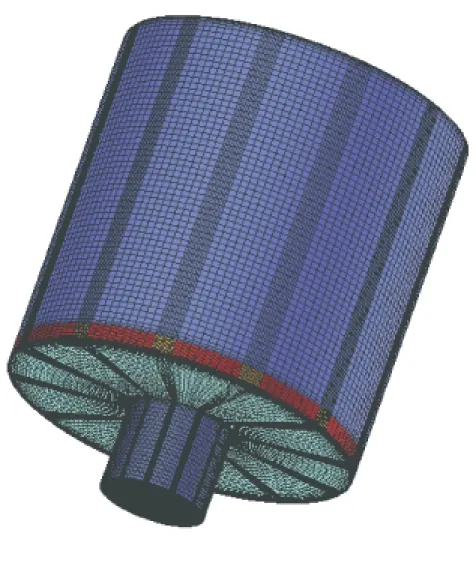
图2 物理模型网格示意图Fig.2 Geometric mesh of physical model
2 计算可信性验证
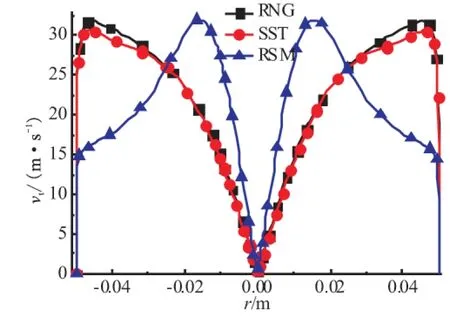
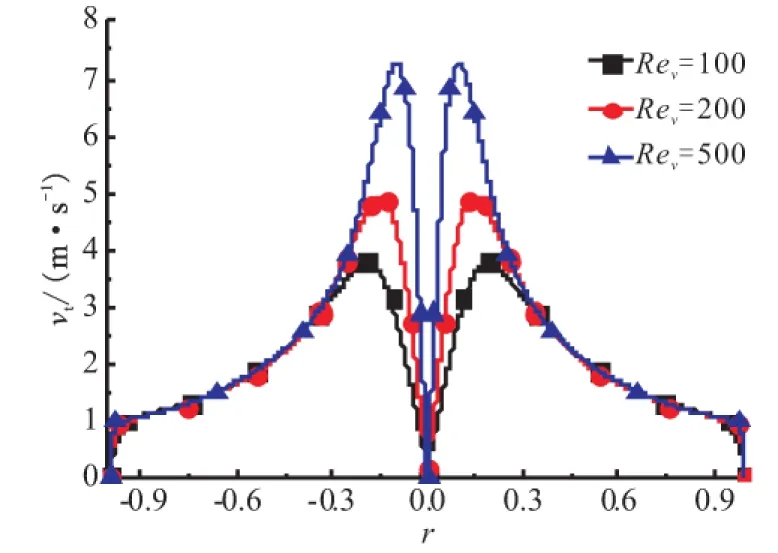
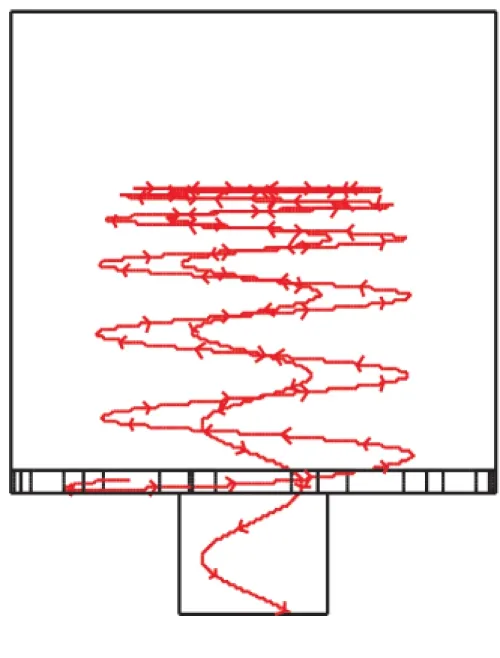
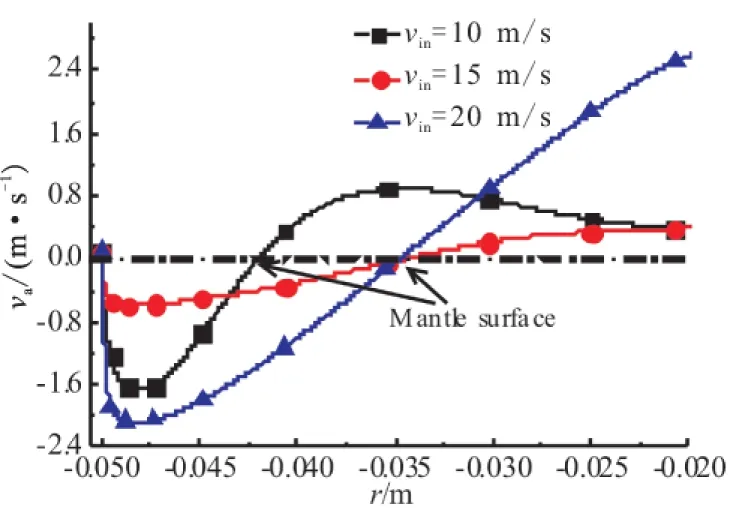
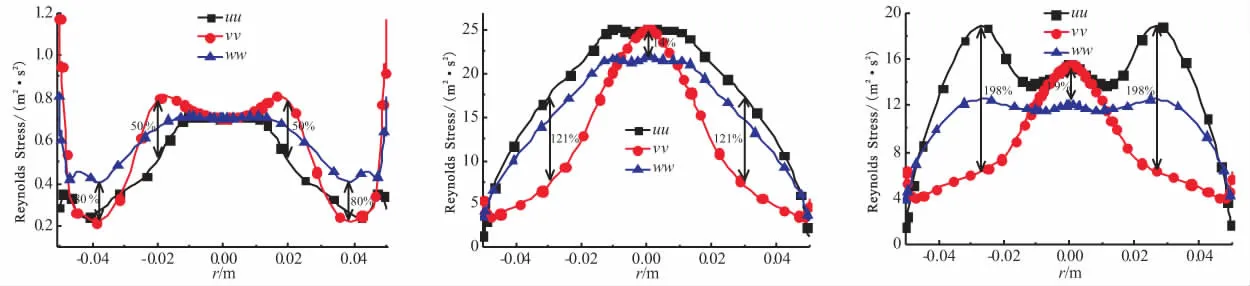
图3为入射速度vin=20 m/s时L=50 mm处无量纲压力差径向分布曲线,3条曲线分别为RNG、SST以及RSM模型计算所得,并与文献[15]中实验数据进行了比较,文献[15]中只给出了0.00 图4所示为本文中RSM模型计算所得速度矢量与Majdalani在文献[5]中所得理论速度矢量比较。 图3 L=50 mm无量纲压力径向分布与文献[15]实验数据Fig.3 Non-dimensional pressure difference distribution inradial direction at L=50 mm and experimentalresults in Reference[15] 可看到在不考虑出口对流场的影响时,CFD结果与理论结果非常一致,Majdalani在文献[5]推导过程中忽略了出口直径对于流场的影响,假设出口直径与内涡半径相等,因此内、外涡流动方向相反,不存在回流区。当出口直径小于内涡半径时就会存在如本文中数值计算中所示的回流区。 综合以上压力与速度矢量图比较可知,本文中RSM计算结果与实验数据及理论结果非常符合,说明本文中所采用物理模型、计算网格、边界条件及数值求解方法具有足够的可信度。 3.1 不同湍流模型速度及双向涡流线分析 图5为不同入射速度下L=50 mm处切向速度vt径向分布曲线(图5(a)~(c)所示)。 vin分别为10、15、20 m/s,以及文献[16]双向涡vt理论曲线图如5(d)所示,理论曲线使用模型半径和入口速度对横、纵轴进行了无量纲化。RSM模型所得速度曲线:vin=10 m/s时vt,max位于r≈±0.045 m处,vin=15 m/s时vt,max向轴线位置处移动位于r≈±0.017 m处,vin=20 m/s时vt,max位于r≈±0.015 m处。同时vt,max随vin的提高而增大,说明内部受迫涡强度随vin提高而增大。RNG模型和SST模型在不同入射速度情况下vt,max始终位于r≈±0.045 m处。 图6所示为vin=20 m/s时RNGk-ε模型、SST模型和RSM模型所得双向涡流结构流线图,在物理模型、入射速度及其他边界条件均相同的情况下,3种湍流模型所得流线图差别非常显著。RNG模型和SST模型也可得到双向旋转流动结构,结合图3、图5曲线可知此时并没有形成内部受迫涡,整个流场均为自由涡,所以双向流动并没有延伸至整个内部流场,旋流长度仅为流场长度的2/3,外部涡流半径也仅为流场半径的2/3。RSM模型所得流线则可以形成完整的双向涡流结构。 从引言中可知,基于双向涡流的VCCWC优点在于外部涡流能够对于发动机起到冷壁作用,所以外部涡流半径应接近于发动机半径,内部涡流高速旋转能够缩短化学反应距离。因此,vt,max应位于内部受迫涡范围内,这均与RSM计算结果相一致。 综合图3中压力曲线、图5中速度曲线及图6流线图可知,SST模型和RNG模型不能得到正确的双向涡流场分布,RSM模型能够准确计算得到双向涡流结构。 (b)vin=15 m/s (c)vin=20 m/s (d)文献[16]理论结果 3.2 RSM模型双向涡结构分析 图7为不同入射速度RSM模型计算所得L=50 mm处轴向速度va径向分布曲线。双向涡流内、外涡轴向速度方向相反,因此va曲线与0.00 m/s速度曲线相交点为内、外涡分界面位置,轴线到该分界面距离即为涡幔半径rm(Mantle Radius)。vin=10m/s时,rm≈0.042 m,vin=15m/s时,rm≈0.035 m,vin=20 m/s时rm与vin=15 m/s时基本相同。 (a)RNG模型 (b)SST模型 (c)RSM模型 图8所示为vin=20 m/s时RSM模型所得不同轴向位置处va分布曲线,轴向位置分别为L=25 mm、L=50 mm和L=75 mm。从图8看到,涡幔半径从顶端到出口处略有变化,但是基本保持在0.035 m左右,这与现有文献结论非常吻合[5,11,17]。 图7 RSM 模型计算所得L=50mm处轴向速度径向分布Fig.7 Axial velocity distribution in radial direction atL=50mm using RSM model 图8 vin=20 m/s时RSM模型计算所得不同位置轴向速度径向分布Fig.8 Axial velocity distribution in radial direction in inlet velocity of vin=20 m/s using RSM model 3.3 雷诺应力各向异性分析 从图3~图6看到,基于布茨涅克各向同性假设的RNG模型与SST模型均无法得到正确的双向涡流结构,而RSM模型则能够准确得到完整的双向涡流结构,压力差分布曲线(图3)与实验数值吻合的非常好,对称面速度矢量分布(图4)与理论结果符合较好。从国内外学者关于双向涡流数值计算文章中可看到,部分文章依然采用基于布茨涅克各向同性假设的湍流模型进行数值计算研究。为了证明基于布茨涅克各向同性假设湍流模型的不足,图9~图11将RSM模型计算所得不同入射速度情况下各轴向位置处雷诺正应力分布曲线进行比较分析。 (a)vin=10 m/s (b)vin=15 m/s (c)vin=20 m/s (a)vin=10 m/s (b)vin=15 m/s (c)vin=20 m/s (a)vin=10 m/s (b)vin=15 m/s (c)vin=20 m/s 比较3.1节与本节雷诺正应力分析可知,RNG模型与SST模型无法得到正确双向涡流的原因在于双向涡流结构中雷诺正应力各向异性特性显著,内、外涡分界面附近雷诺正应力最大差值达到198%,且随内部受迫涡强度增大还会进一步提高,此时布茨涅克各向同性假设已经无法满足双向涡流物理特性,因此RNG模型与SST模型无法得到正确的双向涡流,推论可知基于布茨涅克各向同性假设的其他湍流模型,如Standardk-ε模型,Standardk-ω模型等也不适用于双向涡流数值计算。雷诺应力各向异性决定了湍流脉动的各向异性,化学反应数值计算准确性很大程度上决定于湍流场计算的准确性,因此未来无论进行VCCWC冷流或燃烧数值模拟时均应摒弃基于布茨涅克各向同性假设的湍流模型。 (1)基于布茨涅克各向同性假设的RNG模型与SST模型在入射速度从vin=10 m/s增大到vin=20 m/s时均无法准确得到内部受迫涡、外部自由涡的双向涡流结构,RSM模型能够准确得到与实验与理论结果相符的双向涡流结构。 (2)对于本文中所使用的物理模型尺寸,当入射速度vin=10 m/s时无法形成稳定的内部受迫涡,当vin≥15 m/s时形成稳定的双向涡结构,在一定的速度变化范围内涡幔半径保持在rm=0.035 m左右。随入射速度提高内部受迫涡强度增大,因此最大切向速度vt,max增大,其位置随入射速度提高而靠近轴线位置。 (3)当双向涡流形成时,内、外涡分界面附近雷诺正应力各向异性特征显著,且随入射速度的提高而增强,最大差值达到了198%,轴线附近流场雷诺正应力各向异性特征相对较弱,但是最大差值依然达到46%,因此基于布茨涅克各向同性假设的湍流模型不适用于VCCWC双向涡流数值模拟研究。 [1] Chiaverini,M J,Malecki,M J,Sauer,J A,et al.Vortex combustion chamber development for future liquid rocket engine applications[R].AIAA2002-4149. [2] Turner A E.Aquarius low cost launch main engine study[C]//3rd Responsive Space Conference April 25-28,2005 Los Angeles,CA. [3] Munson S M,Sauer J A,Rocholl J D,et al.Development of a low-cost vortex-cooled thrust chamber using hybrid fabrication techniques[C]//47th AIAA/ASME/SA.E/ASEE Joint Propulsion Conference & Exhibit,31 July-03 August 2011,San Diego,California. [4] Chiaverini M J,Malecki M J,Sauer A,et al.Vortex thrust chamber testing and analysis for O2-H2propulsion applications[R].AIAA 2003-4473. [5] Vyas A B,Majdalani J.The bidirectional vortex.part 1:an exact inviscid solution[R].AIAA2003-5052. [6] Vyas A B,Majdalani J.The bidirectional vortex.Part 2:viscous core corrections[R].AIAA2003-5053. [7] Maicke B A,Majdalani J.A constant shear stress core flow model of the bidirectional vortex[J].Proceedings of the Royal Society,2009,465:915-935. [8] Maicke B A,Majdalani J.On the compressible bidirectional vortex.Part 1:A bragg-hawthorne stream function formulation[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition,09-12 January 2012,Nashville,Tennessee. [9] Maicke B A,Majdalani J.On the compressible bidirectional Vortex.Part 2:A beltramian flowfield approximation[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition,09-12 January 2012,Nashville,Tennessee. [10] Fang D,Majdalani J.Simulation of the cold-wall swirl driven combustion chamber[R].AIAA 2003-5055. [11] 唐飞,李家文,常克宇.涡流冷却推力室中涡流结构的分析与优化[J].推进技术,2010,31(2):165-169. [12] 吴东波,李家文,常克宇.GH2/GO2涡流冷却推力室设计与数值计算[J].火箭推进,2010,36(5):17-22. [13] 孙得川,白荣博,刘上.涡流燃烧发动机燃烧室数值模拟[J].弹箭与制导学报,2011,31(2):111-114. [14] Schmitt F G.About boussinesq's turbulent viscosity hypothesis:historical remarks and a direct evaluation of its validity[J].Comptes,Rendus,Mecanique,2007,9-10,335:617-627. [15] Maicke B A,Majdalani J.Characterization of the Bidirectional vortex using particle image velocimetry[D].PhD.Giovanna Cavazzini (Ed.),ISBN:978-953-51-0625-8,InTech. [16] Majdalani J,Halpenny E K.The bidirectional vortex with sidewall injection[C]//44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit,21-23 July 2008,Hartford,CT. [17] Smith,J L.An analysis of the vortex flow in the cyclone separator[J].Journal of Basic Engineering Transactions of the ASME,1962:609-618. (编辑:吕耀辉) Research and analysis of reynolds stress anisotropic in bidirectional vortex simulation DANG Jin-feng,GAO Ye,LIU Jia-ning (College of Aerospace and Civil Engineering,Harbin Engineering University,Harbin 150001,China) In this paper,simulation results were compared with experimental data and theoretical results.The simulation validity of RNGk-εmodel and SST model based on Boussinesq isotropic hypothesis and RSM model in bidirectional vortex were discussed and bidirectional vortex properties in different inlet velocities were analyzed as well.It is pointed out that the RNG model and SST model could not achieve the bidirectional vortex which frees in outer area and is forced in inner space under any inlet velocity based on Boussinesq isotropic hypothesis,while the RSM model simulation results fit the experiment data and theoretical solutions well.In mantle surface of inner vortex and outer vortex,Reynolds stress anisotropy characteristics is significant and is strengthened with the increase of inlet velocity.The biggest difference between normal stresses inx,y,zdirection can reach up to 198%.In core flow area close to axial,Reynolds stress anisotropy is relatively weak,but the greatest difference can still reach as large as 46%.Therefore,it is believed that turbulent models based on Boussinesq isotropic hypothesis are invalid in VCCWC simulation. bidirectional vortex;vortex combustion cold-wall chamber;reynolds stress;anisotropic 2014-10-30; :2014-12-11。 自然科学基金面上项目(11372079)。 党进锋(1987—),男,博士生,研究方向为发动机内流场数值仿真。E-mail:xiandjf@163.com V430 A 1006-2793(2015)05-0640-06 10.7673/j.issn.1006-2793.2015.05.007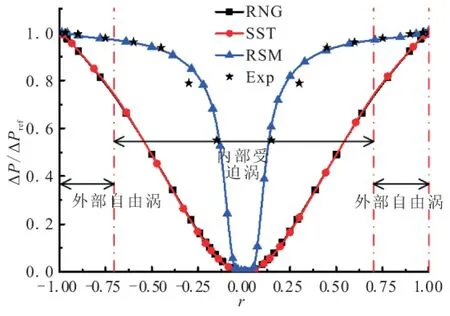
3 计算结果及讨论






4 结论

