基于IAHP－可拓理论的城市道路与高速公路衔接路段评价

李 嵘，刘 艳，刘玉露

（1.武汉铁路职业技术学院 实训中心，湖北 武汉 430205；2.湖北楚天高速公路股份有限公司 工程技术部，湖北 武汉430074；3.湖北省交通运输厅随岳高速公路管理处 第三养护管理站，湖北 武汉430050）

城市道路与高速公路的衔接路段是连接城市的枢纽，是实现城市道路网与高速公路的有机协调衔接。目前，我国高速公路里程成为世界第一。衔接路段的优劣关系到整个交通系统的效率。1950年以后，随着世界城市交通以及高速公路的快速发展，美国、德国以及日本等欧美国家就已经开始对衔接路段的综合效益进行了分析。经过60多年的研究，已经有了规范及成果。21世纪以后，我国开始对衔接路段进行研究。刘进民、王军丽、李谆对衔接道路的评价体系以及路网的优化进行了研究分析。张碧琴，闫向阳，王慧建立了基于AHP的多级模糊综合衔接路段评价方法。王花兰，梁院生建立了衔接路段的多级可拓评价模型并且通过实际案例进行了应用分析。然而，在国内衔接路段的研究，还没有建立其评价指标体系规范，而且由于衔接路段的评价指标影响因素较多，评价结果的有效性和准确性也难以保证。通过上述分析发现，我国现阶段的衔接路段进行评价时还需要结合主观经验。层次分析理论（AHP）适应于衔接路段评价的特点，是近期可行的方法。但是应用AHP时，有时元素之间影响的高低程度很难用一个精确的数来表达（例如:评价指标处于“重要”与“特别重要”之间时），适用区间数来表示结果则更加合理。同时，有时可能由于专家的失误从而造成评估的准确性降低。因此，本文引入基于可拓理论的群决策区间层次分析法（GIAHP）来比较区间数大小的相对优势度排序方法，找出对评价结果影响大的指标，给出其敏感指标的排序，提高高速公路决策结果的合理性。鉴于衔接路段评价指标之间存在着模糊性、多目标性，使用模糊综合评价理论，期望为衔接路段评价提供参考，提高衔接路段评价的有效性。

1 评价指标体系的构建

衔接路段是城市对外交通的主要连接通道，衔接路段的优劣直接影响整个交通系统的效率。高速公路与城市道路衔接路段评价就是合理的分析现役的该路段的等级，以便查找运营管理中存在的问题，从而采取措施来提升人－车－路－环境的综合效益。建立衔接路段的评价指标，本质就是要寻找能全面反映该路段各方面的特征指标。通过对衔接路段的实际分析，参照文献建立如图1所示的评价指标体系。

图1 衔接路段综合评价体系

2 衔接路段综合评价指标分析

2.1 安全影响指标

2.1.1 衔接路段特大事故Sx

特大事故是指一次造成死亡3人以上，或者重伤11人以上，或者死亡1人，同时重伤8人以上，或者死亡2人，同时重伤5人以上，或者财产损失6万元以上的事故。衔接路段的特大事故的多少是路段合理性的重要指标。

2.1.2 衔接路段的死亡强度Dx

Dx反映的是衔接路段车辆行驶的重要安全特征。Dx指标涵义:死亡人数（D）与区域交通基准量（W基）之比。

2.1.3 交通事故多发点率Ux

Ux交通事故多发点率指标涵义:交通事故多发点（U）与衔接路段长度（L）之比。

2.2 交通环境指标

2.2.1 衔接路段绿化率

绿化率是路段可持续的发展的重要特征。它的涵义是实施绿化路段的比率，是指道路红线范围内各种绿带宽度之和占总宽度的百分比。

2.2.2 衔接道路汽车尾气排放达标率p

p定义为衔接道路汽车尾气排放达标里程与总里程之比值。排放达标率算式

2.2.3 衔接道路交通噪声达标率q

q的评价依据是我国的城市交通噪声标准，衔接道路两侧噪音大小的平均值应遵循该标准。算式为3

2.3 运输服务指标

2.3.1 平均行程车速V平

V平是衔接路段服务质量的重要指标。算式为

式中:L为衔接道路的长度（km）；N为衔接道路小时交通量（veh／h）；ti为第i辆车的行驶时间（h）。

2.3.2 衔接道路的拥挤度Y

Y是判断衔接路段使用是否拥挤的重要指标。算式为

式中:qi为衔接道路中第i个路段的交通量（veh／d）；Ci为衔接路段中第i个路段设计交通量（veh／d）；Li为第i个路段里程（krn）。

2.3.3 单位里程平均延误T延误

T延误指标越大，交通越拥堵。算式为

式中:V行程为实际行驶速度（km／h）；V自由为自由流速度（km／h）。

2.3.4 非直线系数k

k是指两节点的实际里程（l）与两点间空间距离（s）的比。算式为

2.3.5 交通负荷度s

s反映链接路段的路网能力和适应情况。算式为

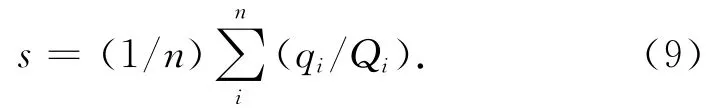
式中:qi为第i路段的实际交通量；Qi为第i路段的设计交通量。

2.3.6 平均饱和度f

f反映路段利用率，指实际分配交通量与设计通行能力的比。算式为

式中:vi衔接道路i的分配交通量，ci衔接道路i的通行能力。

其他的指标由交通规划师、城市规划师、交通工程师等结合实际，进行定量化分析。

3 IAHP－可拓模糊综合理论的评价

3.1 基于区间层析理论初步确定指标权重

3.1.1 构建

与AHP方法相似，构建目标层A，准则层B及指标层C

3.1.2 构造互补

参照文献利用1／10－9／10标度法来构造互补判断矩阵R（xij），即

3.1.3 一致性检验

令

3.1.4 层次排序计算

首先对R（rij）n×n层次单排序

式（14）、（15）计算指标层对于其准则j的权重wji，准则j相对于目标层的权重λj。

然后进行层次总排序，求权重

3.1.5 比较

区间权重wi的比较，通过比较，得到相对优势度矩阵p

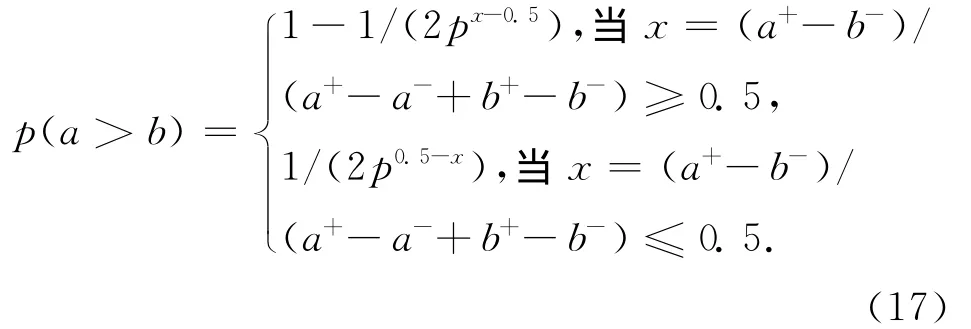
式中:P为区间a与区间b相比较时，a＞b的相对优势度。ρ＞1，一般取2（或者e），此处取2。最后，利用式（12）～（14）得到相对优势度的指标排序。

3.2 基于可拓分析的权重修正

此处引入GIAHP，建立一种基于AHP的群决策模型。设有m位决策者对n个指标使用IAHP得到判断矩阵Aij，然后根据Aij得到权重系数δij。其中，δij表示第i个A通过一致性检验后的第j个决策指标的权重。基于IAHP的可拓理论的多人权重步骤如下

3.2.1 确定经典域物元Roj，节域物元RPj

式中:Roj为第j个指标的经典域物元；RPj为第j个指标的节域物元；aj＝ min（δij），bj＝ max（δij），i＝1，2，3，…，m，j＝1，2，3，…n；

3.2.2 确定待测物元RXj

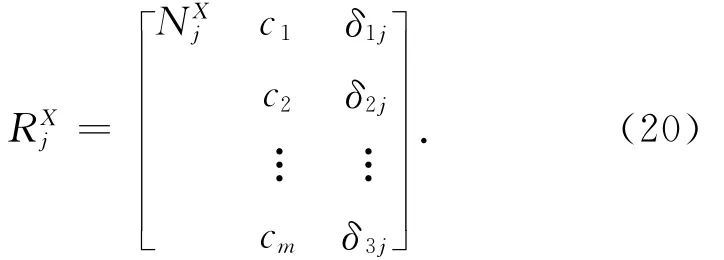
式中:为第j个指标的待测物元；aj＝min（δij），bj＝ max（δij），i＝1，2，3，…，m，j＝1，2，3，…n。

3.2.3 确定关联函数值K（δij）

式中:K（δij）为第i位决策者的第j个指标的关联函数值。

3.2.4 确定关联函数复合物元R0

3.2.5 确定专家的离散系数ki，效度系数φi

3.2.6φi归一化

则修正后的权重为WJ

将所得结果正规化，即得修正后的权重

3.3 模糊评价理论的绿色低碳高速公路综合评价

3.3.1 评价指标的量化

3.3.1.1 定量指标无量纲化

为了能够准确判定指标的等级，需要对指标无量纲化分析。设评价指标xij，其定义域为xij∈［Aij，Bij］，Aij＞0，Bij＞0，Aij＜Bij，yij为无量纲化后的结果。成本型指标和效益型指标的无量纲化函数式为

成本型指标

效益型指标

3.3.1.2 定性指标量化

针对定性指标采用评价等级隶属度的方法来进行确定。本文参照文献将定性评价指标分为5个等级（优、良、中、次、差）。

3.3.2 模糊综合评价

最终模糊综合评价结果向量Y参照文献分为分为5个等级（优、良、中、次、差）作为评价结果。

4 案例分析

4.1 案例描述

荆州市某高速公路于2010年12月完全通车，此段有长江大桥连接湖南省岳阳市。随岳高速公路与岳阳市相连接，并通过荆岳长江大桥与互通式立交相连接。随着岳阳市的发展，岳阳市周边的城市不断发展，通过链接路段的对外交通出行逐渐增加，调查随岳高速与岳阳市的链接路段能否满足日益快速增长的交通需求十分必要。具体所需的评价数据如表1所示。

表1 随岳高速与岳阳市链接路段综合评价指标实测表

4.2 IAHP初步确定权重分析

依据图1建立评估模型。选择4个专家群分别构造区间层次判断矩阵，依据式（11）～（18）求解P。以专家群1为例利用式（18）求P:

利用式（12）～（14）得到相对优势度的指标排序。专家群1权重如下:

4.3 基于可拓分析的权重修正

对其他3个专家群的权重进行集结并进行一致性检验。权重见表2。

表2 不同专家的权重

由式（19）～（23）计算专家的离散系数ki。由式（24）～（25）计算修正后的权重专家权重。结果如表3所示。

表3 修正后的权重专家权重

由式（26）计算修正后的指标权重，结果如表4所示，相应的指标排序如图2所示。

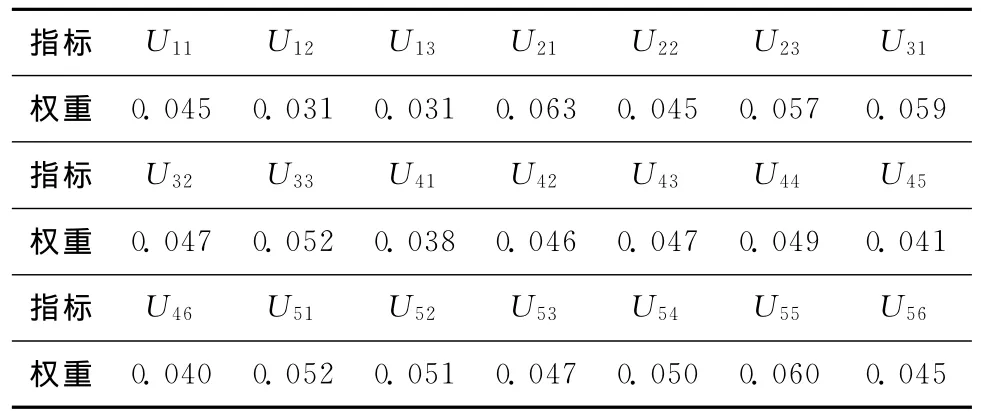
表4 修正后的指标权重

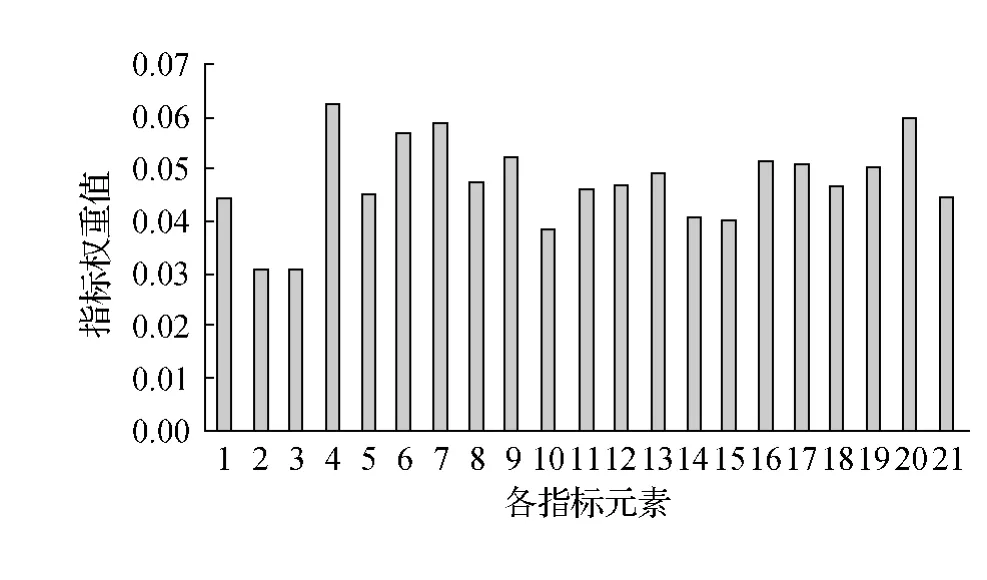
图2 各指标的相对重要度示意图

4.4 模糊综合评价

4.4.1 确定因素集和评语集

根据衔接路段优劣的程度，将其划分为优、良、中、次、差5个级别。衔接路段评价指标的评估级别为U＝｛U1，U2，U3，U4，U5｝＝｛优、良、中、次、差｝。综合评价指标隶属度如表5所示。

表5 链接路段综合评价指标隶属度

4.4.2 建立评价矩阵

对定性指标采取专家打分法获得。定性指标的值如表6所示。

表6 定性指标得分

4.4.3 模糊综合评价

依据式（27）综合评价为:H1＝W21·R1＝（0，0.106，0，0，0）；H2＝W22·R2＝ （0.073，0.054，0.028，0.006，0）；H3＝W23·R3＝ （0，0.047，0.052，0.059，0）；H4＝W24·R4＝ （0，0.125，0.137，0，0）；H5＝W25·R5＝ （0.064，0.107，0.099，0.034，0）。

4.5 结果分析

最终模糊综合评价结果向量Y参照文献可作为评价结果。

依据模糊综合评价最大隶属度原则，随岳高速公路与岳阳市的链接路段的安全影响指标（max＝0.106）为“良好”等级；经济效益指标（max＝0.073）为“优秀”等级；交通环境指标（max＝0.059）为“次级”等级；运输服务指标（max＝0.137）为“中等”等级；交通协调指标（max＝0.107）为“良好”等级。通过1级评价计算以及实际调研分析，该段的高速公路公路刚刚经历了中修工程，一些绿色低碳的设备、设施在不断的完善中，以后的管理会得到改善和突破。通过综合等级分析，衔接路段综合指标（max＝0.440）属于良好等级。随岳高速公路与岳阳市的链接路段的综合评价结果为“较好”。

上述结果说明，随岳高速与岳阳市的链接路段能够满足现阶段的交通发展。

5 结 论

1）针对目前衔接路段评价缺少合理的综合评价指标体系的问题，以GIAHP为基础的指标权重计算方法，客服了决策人员因失误或者偏好等使权重出现偏差的问题，为最终评价提供依据。同时，由于衔接路段的评估具有模糊性和不确定性，建立衔接路段的多级模糊理论评级模型。

2）运用GIAHP多级模糊模型对随岳高速公路与岳阳市的衔接路段的程度进行评价，得出衔接路段的价等级，从计算过程和结果可以看出该方法有效。

但是，由于评价因素多，不确性条件较多，GIAHP多级模糊评估模型中的一些定性因素还不能有效的定量化，这也是以后需要改进的地方。

［1］ ITE Committee.Panning urban arterial and freeway systems［S］.2000.

［2］ 陈培健.城市发展与对外公路交通合理布局的研究［J］.公路交通科技，2000，17（3）:36－39.

［3］ 徐文学，邹志云，余斌，等.高速公路网与城市道路网衔接研究［M］.武汉:湖北科技出版社，2008.

［4］ Coleman S B.Planning urban arterial and freeway systems［J］.ITE Journal，1997，67（8）.

［5］ 刘进民.高速公路与城市道路衔接道路布局规划研究［D］.武汉:华中科技大学，2007.

［6］ 王军丽.高速公路过境模式与城市形态的关系研究［D］.武汉:华中科技大学，2007.

［7］ 李谆.城市道路与高速公路衔接道路网综合评价研究［D］.武汉:华中科技大学，2007.

［8］ 张碧琴，闫向阳，王慧.基于AHP的模糊综合评价方法在高速公路与城市道路间衔接线综合评价中的应用［J］.公路，2013（4）:139－144.

［9］ 王花兰，梁院生.高速公路与城市道路间衔接线综合评价［J］.兰州交通大学学报，2013，32（6）:90－96.

［10］王慧.高速公路与城市道路衔接段研究［D］.西安:长安大学，2012.

［11］吴焱，钱振邦，王建军.高速公路交通安全风险评价与敏感性分析［J］.长安大学学报:自然科学版，2014，34（4）:134－141.

［12］高会生，郭爱玲，于晓东.基于区间层次分析法的网络安全风险评估［J］.电力科学与工程，2009，25（3）:64－67.

［13］刘玉露，胡万欣，蒋晶尧，等.基于多人决策分析的多属性预防性养护决策［J］.交通科学与工程，2014，30（2）:95－100.

［14］刘玉露，胡万欣，胡怡玮.基于多属性群决策层次分析的预防性养护措施决策研究［J］.公路工程，2014，39（5）:342－346.

［15］刘艳，胡怡玮，刘玉露.基于模糊评价法的武汉雨天交通安全分析及对策研究［J］.浙江交通职业技术学院学报，2013，14（1）:21－24.

［16］程巧梦，张广泰，王立晓.基于AHP的城市道路交通安全评价指标体系［J］.交通科技与经济，2014，16（5）:1－4.

［17］曹林，高呈，赵凯，等.AHP权重决策的铁路车站信号楼作业安全等级评价［J］.交通科技与经济，2014，16（2）:44－47.