基于层次分析法的干线公路可变限速研究
姜雪娇,郭唐仪
(南京理工大学 自动化学院,江苏 南京210094)
随着居民生活水平的提高,汽车的保有量大幅度增加,现有的干线公路尽管不断被扩建,但仍无法满足越来越多的车辆需求,如何保障一条通畅、安全、舒适的道路已成为当前研究的重点。为充分挖掘公路的潜在能力,一种主动式的交通管理控制方式——可变限速(VSL,Variable Speed Limit)被提出,它以一种积极的、动态的、自动的方式对速度进行管控,利用计算机及相应的传感器、监控系统等技术实时获取交通信息,基于这些信息对相应公路上的速度进行管理控制,并在缓解交通拥堵、降低事故发生率等方面起到了重要作用。
1 可变限速影响因素及速度设定值的确定
1.1 可变限速影响因素的确定
对于干线公路,影响行车速度值变化的因素较为复杂,不仅有单个因素的单独作用还可能存在多个因素间的相互作用,为了覆盖全部的影响因素,将影响因素的类型分为五大类:道路、交通、车辆、环境和管理,由于车辆主要是指车辆性能方面的内容,对可变限速的影响不大,因此不考虑车辆部分。根据类型再进行细化,得到如图1所示的可变限速影响因素构成图。
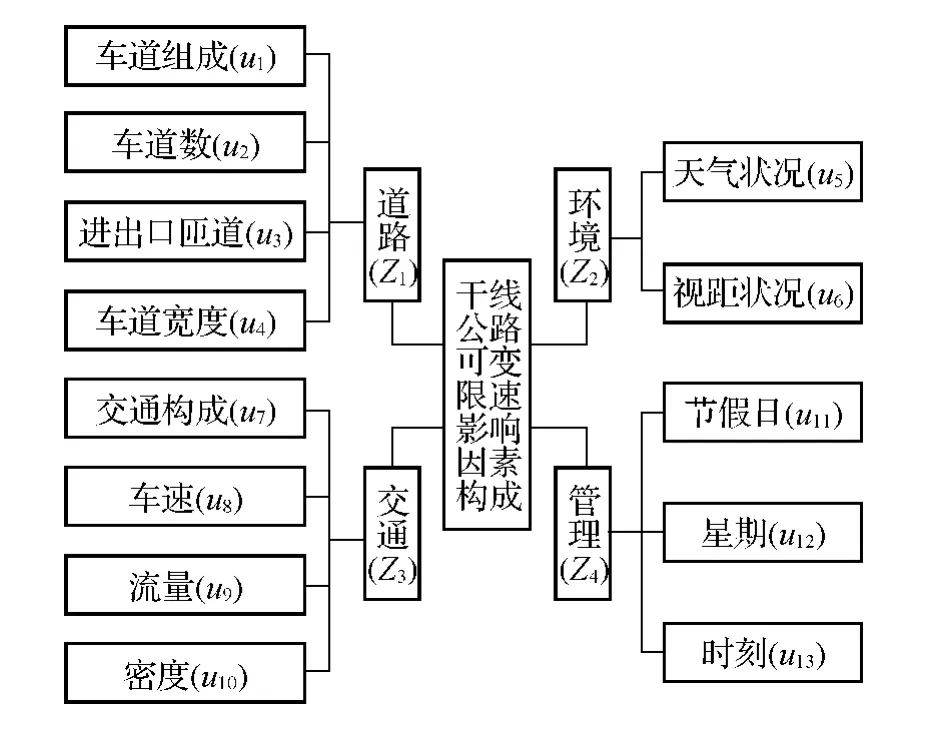
图1 干线公路可变限速影响因素构成
1.2 速度设定值的确定
根据公式V=Vf(1-K/Kj),从密度入手,分析不同密度区间的速度值,即可确定可变限速的限速值。隽志才等根据计算机数据模拟获得的不同交通量下的速度值,得到干线公路上的限速值,取值在30~80km/h,以10km/h作为间隔,可以得到6个限速值,VSL(i)={30,40,50,60,70,80}。
基于理论研究可以得到在单个影响因素u1~u8作用下的小轿车建议速度。其中,车速影响下的建议速度u8为理想状态下的干线公路限速值。根据周蔚吾《道路交通标志标线设置技术手册》中道路限速设置原则,对普通干线公路而言,当分车道或分车型时,最右侧为快车道,设置最高限速为80km/h,最低限速50~60km/h,以此依据确定u1;当车道数减少到2车道时,限速值需调整为60~70km/h,以此依据确定u2;当连接进出口匝道时,入口匝道一般不设置任何限速,出口匝道按照警告限速,设计速度为主线车道速度的80%~50%,即35~65km/h,以此依据确定u3;当路宽变窄,车道数不减少时,可以不考虑限速值的改变,即取理想状态下建议车速为80km/h,以此依据确定u4;当遇能见度较低的恶劣天气或照明条件不利的夜间道路时,按照法规限速,限速值为最低30km/h,以此依据确定u5,u6;当存在混行交通时,按照法规限速,限速值为40~50km/h,以此依据确定u7。
基于实验数据可以得到在单个影响因素u9~u13作用下的小轿车建议速度。如图2所示,当交通量较大、车流密度较高时,驾驶员的心率增长率与速度存在一定的关系,当速度高于50km/h时,心率增长率变化较大,因此大流量、高密度区域的限速值建议取40~50km/h,以此依据确定u9,10;节假日、早晚高峰等特殊时段也存在交通量变大、车流密度变高的现象,当速度处于40~55km/h时,心率变化较稳定,以此依据确定u11,u12,u13。

图2 不同速度下增长率的变化曲线
为降低层次分析法中人的主观性对结果所造成的影响,本文采用三标度法取代九标度法。根据上述分析,确定出单个影响因素下的最优建议车速,并依照速度差度和专家打分情况给出优、良、差三个等级下的建议速度,如表1所示。
2 基于层次分析法的可变限速
层次分析法是一种定性与定量相结合的多目标决策分析方法,利用层次分析法解决可变限速问题,可以将复杂问题简单化,通过分解多目标为若干层次与因素,构建出层次分析法的层次结构图,并将两两指标进行重要程度的比较判断,构建判断矩阵,获得基于不同方案下重要程度的权重值,即可得到方案优劣的排序并确定出最优方案,即所需的限速值。典型的层次结构包括目标层(A)、准则层(C)和方案层(P)三部分,下面为利用层次分析法确定可变限速权重值的步骤:
2.1 明确目标
决策目标是在不同外界交通环境条件下确定不同的限速值。
2.2 建立层次结构
建立层次结构图,确定A、C、P三个层次的内容及相互间联系,如图3所示,在准则层中包括准则C1与子准则C2两部分,子准则C2为准则C1的详细化,在构建判断矩阵时使用子准则部分进行分析。
2.3 建立判断矩阵
在准则层间构建判断矩阵,即因素的重要性次序。对于道路、环境、交通、管理四方面因素而言,交通始终是随道路、环境和管理因素变化而变化的因素。从保障交通安全的角度出发,可变限速的宗旨是解决特殊情况下容易造成交通事故区段的安全问题,因此因素的重要性次序应从影响行车安全程度大小的角度出发,通过整理分析往年交通事故发生原因,根据专家的观点,即可给出因素间的重要性次序:u5>u6>u9(10、11、12、13)>u3>u1>u2(4)>u8>u7。
在基于不同准则下的方案层之间构建判断矩阵,即不同准则下方案层各方案间的重要性次序。判断矩阵的构建可参照表1所示进行,判断矩阵的构建采用三标度法,取值按以下原则选取:重要程度i(行)远高于j(列)取5,i高于j取3,i约等于j取1,i低于j取1/3,i远低于j取1/5。
C2层关于目标层的判断矩阵B1为


P层关于准则层的判断矩阵为Bx(x=2~14),P层对u1元素。判断矩阵为

同理,可以分别针对元素u2~u13建立起P层Vi间的判断矩阵。
2.4 进行层次单排序
对判断矩阵进行正规化得到Wi=Si/∑Si。假设 判 断 矩 阵B= [b11,…,b1n;bi1,…,bin;bn1,…,bnn;];那么S1=b11+…+b1n;Si=bi1+…+bin;归一化处理后,通过对比可得Wi的大小,即可得到关于判断矩阵的各元素影响程度的单排序。
2.5 进行层次总排序
层次总排序是在对判断矩阵B1中得到的各子准则ui的重要程度排序的基础上,以各子准则ui的权重为参考,对在13个关于方案层P的判断矩阵Bx也就是不同准则下限速值的重要程度排序再进行一个总体的排序,获得最后所需的某种交通环境条件下的可变限速值V。
需要注意的是,在实际应用中,构建的不同准则下关于P层的判断矩阵Bx的数量小于等于13,因为不同交通环境条件下考虑的因素是不一样的,在13个影响因素中选取出所需考虑的因素作为构建层次结构的准则层元素,并套用2.5节中的判断矩阵,最后利用计算机程序(如Matlab)辅助完成所需判断矩阵求解,即可得到所需的可变限速值。

图3 可变限速层次结构模型
3 仿真验证
3.1 判断矩阵进行一致性检验
计算判断矩阵求得权重的方法一般有几何平均法、算术平均法、特征向量法和最小二乘法4种方法。由于构建的判断矩阵为正互反矩阵,因此利用特征向量法进行计算是最为广泛的,而利用特征向量求解矩阵的前提条件是正互反矩阵为一致性矩阵。因此,在利用特征向量法求解之前对所构建的判断矩阵进行一致性检验尤为重要。
判断正互反矩阵是否为一致性矩阵有如下定理:即当A的最大特征值λmax=n(矩阵阶数)时,正互反矩阵A为一致性矩阵。而由于一致性矩阵的要求过高,在实际中很难保证建立的判断矩阵完全满足一致性矩阵的要求,因此引入一致性指标(C.I.,Consistency Index)C.I.= (λmax-n)/(n-1)和平均随机一致性指标(R.I.,Rondom Index)R.I.=(λmaxp-n)/(n-1),将计算所得的C.I.与已知的R.I.进行对比得到一致性比率C.R.=C.I./R.I.,当C.R.<0.1时,则认为判断矩阵 A满足一致性,反之则需要对判断矩阵进行修改后重新确定其一致性。其中不同阶数矩阵的随机一致性指标R.I.如表2所示。

表2 不同阶数矩阵的随机一致性指标R.I.
若判断矩阵的阶数较大,那么手动计算最大特征值就显得较为困难,可以借助Matlab中的eig函数和max函数,首先利用eig函数求解出判断矩阵的所有特征值,再利用max函数找到所有特征值中的最大特征值,具体的程序过程会在下面的权重计算中给出。
3.2 利用Matlab进行权重计算
利用Matlab对层次分析法建模,构建ahp函数,完成判断矩阵一致性检验和层次单排序以及总排序,最后直接得到各方案的权重值。构建完函数后,在实际限速值权重计算时,只需根据实际情况选择所需判断矩阵,并将判断矩阵的值依次输入函数中即可。
以南京市某干线公路为例,共三条车道,分车道行驶,限速时段为早高峰,限速路段较为拥挤,车头时距小于1s,天气状况良好。
分析给出的实际情况,提取所需指标,主要包括车道组成u1,交通构成u7,车速u8,时刻u13四因素,并提取四因素所对应判断矩阵B2,B8,B9,B14。在Matlab中利用ahp函数输入变量C即可完成可变限速值的确定,具体求解过程如下所示:
1)在Matlab中建立函数文件“ahp”,将自定义编写的层次分析法函数代码输入到弹出的界面Editor中,保存后回到主界面;
2)从B1中确定u1,u7,u8,u13的判断矩阵,即

3)将B1,B2,B8,B9,B14四个判断矩阵输入主界面并开始运行,其中代码分别包括判断矩阵和所对应的逻辑数组,即两层之间是否存在支配与被支配关系。最后输出权重w1,2,3,4,5,6=0.084 6,0.176 1,0.306 6,0.256 0,0.110 5,0.066 2。最高权重w3对应限速值50km/h,为建议限速值,图4为输出限速值的权重图。

图4 输出限速值权重
如图4所示,得到选取限速值的优先顺序为:V3>V4>V2>V5>V1>V6。调整限速值50km/h与60km/h的权重值相差16.5%,下降幅度较小,因此实际情况下的限速值可以在50~60km/h之间因地制宜灵活选取,如若限速路段为过境公路,限速值可以相对较高选取60km/h;如若限速路段为穿城公路,可选取50km/h为限速值。
4 结束语
层次分析法是一种将多因素层次化、通过比较关联因素进行分析和预测的决策方法,其定量与定性相结合的方法使其产生主观性较强,以及计算繁琐的局限性。为克服此局限性,在Matlab平台上建模,解决了计算繁琐的问题;在对各影响因素的速度值确定和判断矩阵的建立中严格遵循相关的法规、标准及实验数据的规律,用三标度法代替九标度法,将主观性降到了最低。本文所述的模型考虑了多方面影响速度的因素,为干线公路限速设计提供了新思路。
[1] 隽志才,姚宏伟,朱泰英,等.高速公路可变限速系统的社会经济影响评价[J].公路交通科技,2004,21(5):104-108.
[2] 周蔚吾.道路交通标志和标线设置技术手册[M].北京:知识产权出版社,2007.
[3] 梁新荣,刘智勇,徐建闽,等.高速公路多路段的模糊逻辑协调控制[J].华南理工大学学报,2005,33(5):35-40.
[4] 撒元功,徐建闽.基于神经网络预测模型的高速公路递阶控制[J].暨南大学学报,2002,23(5):31-34.
[5] 贺敬凯,徐建闽.基于BP神经网络的入口匝道控制器的设计[J].华南理工大学学报,2002,30(7):24-27.
[6] 郭金玉,张忠彬,孙庆云.层次分析法的研究与应用[J].中国安全科学学报,2008,18(5):148-153.
[7] 邓雪,李家铭,曾浩建,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,42(7):93-99.
[8] 安一凡,梁院生,王花兰.基于组合赋权法的高速公路应急管理能力评价[J].交通科技与经济,2015,17(1):5-9.
[9] 郭东硕,程正敏,彭茜.基于Matlab的层次分析法及其运用浅析[J].信息技术,2010(11):269-270.

