基于VISSIM软件的淮安市翔宇大道交通仿真
张振栋,苏栋辉
(1.上海理工大学 管理学院,上海 200093;2.南京航空航天大学 民航学院,江苏 南京 211106)
1 交通仿真的必要性
随着私人小汽车数量的逐渐增加,城市机动车保有量呈直线上升趋势,产生了各种各样的交通问题。这些交通问题需要交通管理部门实施科学的措施和方案去解决。但大多数改善道路交通方案的实施往往需要对交通基础设施进行大范围的改造,但在改造之前,由于缺乏必要的仿真模拟而无法提前对改造后道路交通的改善状况做出科学评价,导致改造方案缺乏科学性。
近几年来,随着计算机技术的不断发展,利用计算机进行交通仿真已成为解决交通问题的重要途径。基于计算机的交通仿真技术,在交通工程领域实现了大规模的应用。交通仿真技术的优势在于:第一,能够节省大量的人力、物力进行真实的模拟交通状况,尤其适用于对规划中的道路进行模拟;第二,比同类软件有着更广的适用范围;第三,能够多次重复进行试验,从而合理地选择不同的设计方案。
由于国外在交通仿真技术方面的应用已步入商业化阶段,且国内相关技术还不完善,因而目前国内主要使用国外引进的微观仿真软件。这些仿真软件的开发基本上都是根据国外交通的特点而设计的,因此引进到国内后直接应用时,得到的仿真结果往往与国内的实际交通状况差别较大,缺乏科学性,模型的相关参数需要修正。所以说,构建交通仿真模型的关键步骤是模型的参数标定。
2 交通仿真理论
本文所使用的VISSIM软件是由德国PTV公司开发的微观仿真软件系统。VISSIM软件的适用范围十分广泛,它不仅能够模拟城市一般道路和城市快速路的交通流状况以及交叉口信号控制方案的优化,同时还能应用于高速公路,如车辆速度控制、交通诱导、高速公路收费系统以及高速公路进出口匝道的设计。
2.1 交通软件仿真理论
VISSIM软件通过软件内部两个组成部分之间交换检测器数据和信号状态信息,实现交通仿真。VISSIM软件的核心是一个由微观交通仿真模型组成的交通仿真器,它是一个采用了以德国卡尔斯鲁厄大学 Wiedemann教授的“生理-心理驾驶行为模型”为基础的车辆跟踪模型。该模型的基本概念是:当在车流中跟随前车行驶的后车驾驶员认为其与前车间的距离小于驾驶员认定的极限时,后车驾驶员就会采取一定的措施降低车速。并且后车会以一个不超过前车速度的车速跟驰,直到后车驾驶员认为与前车间的距离可以安全行驶时,后车驾驶员才会加快车速,并开始形成一个不断重复、循环的过程。
VISSIM软件实现其功能必须依赖于诸多模块,而各种模块所起的作用也不同。通过各种模块的相互配合协作,才能使交通仿真模型接近现实,模拟出交通状况。发挥基础性作用的模块主要包括了交通量定义模块、车辆定义模块、车速分布模块、车辆跟驰模块、车道变换模块等。
2.2 交通仿真参数标定原则
要想使仿真模型能够精确地描述整个仿真过程,就必须在实际的交通运行状态基础上,调整仿真模型中的相关参数。由于交通网络的运行状况会受交通流特性、交通控制运行参数和驾驶员行为特性等参数影响,因而需要对这类参数进行校正。参数校正的最终目的是使整个仿真过程与真实的交通状况基本一致,从而达到模型输出数据与实际测量结果的差异最小。
由于某些因素的存在,如各地的交通特性不同而影响到交通仿真得到的仿真结果,交通仿真模型的某些参数提供给用户,根据实际交通状况进行选择和调整,以弥补仿真软件在某些方面存在的不足。在实际选择时,需要遵循一些要求:第一,选择易在实际交通状态中测量得到的参数,如果参数不能在实际中调查得到,该参数就缺乏了一定的科学性与精确性;第二,选定的参数能够通过自身的变化快速反应出交通状况的变化,即具有较高的灵敏性。在VISSIM软件中,需要标定的参数主要有车辆期望速度、驾驶员行为以及车辆组成等。
2.3 交通仿真参数标定过程
交通仿真模型参数标定的过程一般分为7个阶段。
第一阶段:对研究目标的定义,交通仿真的目的就是最终仿真模型得到的数据与实际数据接近或相同即可;
第二阶段:确定所需的实际数据;
第三阶段:选择影响因素水平,即确定需要标定的参数,由于某些参数对交通仿真结果有较大的影响,需要把这些参数筛选出来进行标定,使这些参数模拟出与实际相符且更理想的交通状况;
第四阶段:建立仿真结果评价体系;
第五阶段:建立仿真网络;
第六阶段:确定驾驶员的路径行为,为减少实验次数,利用拉丁方格法设计实验,确定需要标定的参数;
第七阶段:评价模型的输出结果,依据仿真结果评价体系,评价仿真得到的结果。如果因某参数而使模型没有得到预期的结果,则应继续对该参数进行标定,直到满足标准为止,结束标定。
3 淮安市翔宇大道交通仿真模型与结果分析
3.1 翔宇大道交通现状
淮安市翔宇大道位于江苏省淮安市清河区与淮安区之间,是市区往返淮安区的主要道路。该道路为一级沥青混凝土路面,双向六车道,与多条市内干道相交。车辆构成主要为小汽车、大客车与货车。其中,翔宇大道与城西北路的十字交叉口是淮安区与淮安市区衔接处的一个车流量较大的交叉口,它是车辆往返淮安市区与淮安区的必经之路。该交叉口附近有千年古镇河下风景区,以及大量居民小区、学校和商业区,使得该交叉口车流量与人流量均较大。而交叉口前路段上的车流量状况对车辆进入交叉口时产生的延误、行程时间、排队时间与车流量等有较大影响(见图1)。
3.2 翔宇大道交通调查与建模
由于交通仿真模型的需要,对翔宇大道多路段进行了交通调查,交叉口交通量调查与车速调查结果如表1、表2所示。
目前,翔宇大道与城西北路交叉口采用四相位信号控制,信号周期长度为130s。具体的信号配时方案如图2所示。仿真参数的选择主要包括车速分布、交通构成、信号参数等。根据交通调查资料与翔宇大道实际道路线形,使用VISSIM软件构建基础交通仿真模型,如图3所示。

图1 仿真路段——淮安市翔宇大道
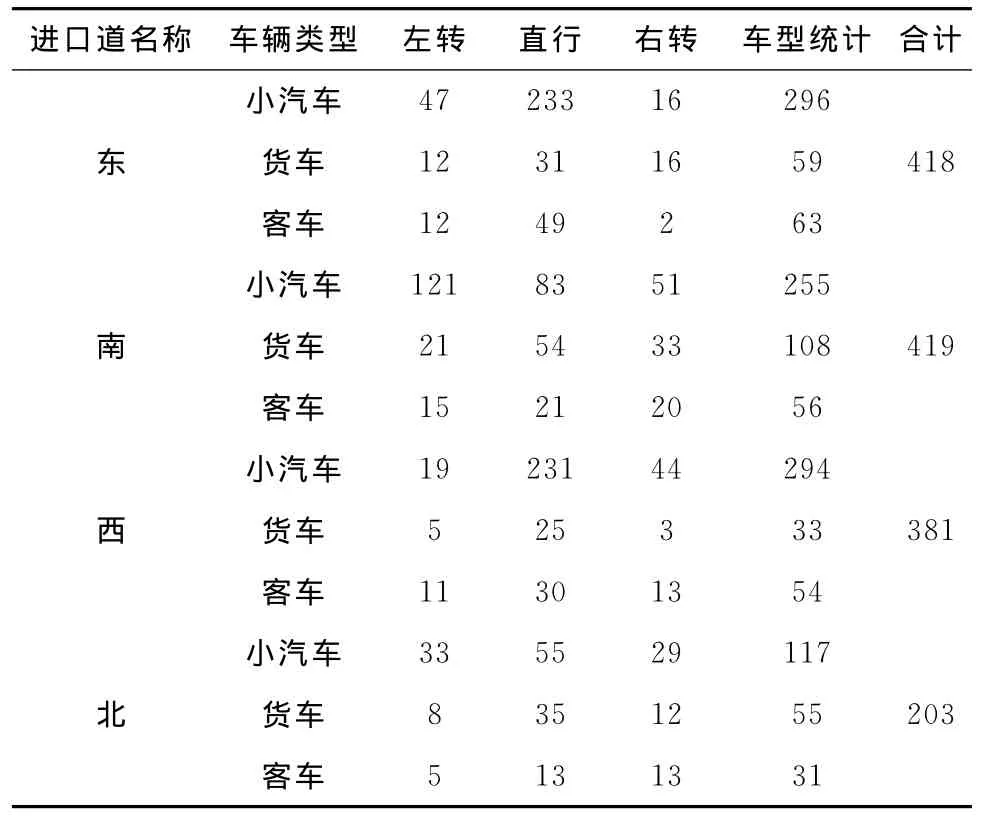
表1 淮安市翔宇大道与城西北路交叉口交通流状况 辆

表2 淮安市翔宇大道车流车速分类统计 km/h

图2 交叉口信号配时

图3 翔宇大道交通仿真路段
3.3 翔宇大道交通仿真模型参数标定
交通仿真模型的参数校正是快速路建模的关键步骤。VISSIM的仿真结果与仿真结果评价指标相接近是此次参数标定的目标,在此次仿真中把路段小汽车与客车速度作为评价指标。
在本次VISSIM仿真中,最小车头时距、等待换道消失时间、紧急停车距离、平均停车距离、车道变换距离以及观察前车辆数是主要的可控参数。首先选择适合用于城市道路的Wiedemann74模型作为汽车跟驰模型。最小车头时距在VISSIM软件中预设的缺省值为0.5m,但在实际调查中最小车头时距大于0.5m。因此,为使其数值符合实际,且有较大浮动范围,将取值范围定为0.5~4.0m。模型中等待换道消失时间的缺省值为60s,但考虑到本次路网的长度以及有交叉口红绿灯信号控制,车辆的实际等待换道消失时间比缺省值长,因而取等待换道消失时间为80s。紧急停车距离的缺省值为5m。平均停车距离在模型中的缺省值为2m。考虑到我国目前司机在停车排队等待时停车位置的随意性较大,无法得到一个较为平均的数值,所以取1~3m的范围。车道变换距离由于与之前的紧急停车距离相联系,而且在实际驾驶过程中司机一般变道所花的时间基本相差无几,因而车辆行驶的距离也基本相同,所以该参数一般采用缺省值为200m,观察前车辆数也取其缺省值为2辆。这样,基本确定了3个需要标定的基本参数:最小车头时距、平均停车距离、观察前方车辆数。
交通仿真模型的标定主要通过运行模型后得到的数据建立函数模型,再找出与实测数据在一定范围内相接近的参数组合。为减少实验的次数,同时保证实验的科学性,采用拉丁格法。根据拉丁方格法,将3个需要标定的参数,即最小车头时距、平均停车距离、观察前方车辆数等三个参数放入一个3×4的拉丁方格中。其中,把平均停车距离和观察前方车辆数作为关键因素,把最小车头时距作为安排因素,共进行4×4=16次试验(见表3)。

表3 随机组合排列表
依次试验每一组参数组合。试验前,还需要在模型的多运行模式窗口选择随机种子数,最后可得到每组参数组合模拟后输出的相关参数。由于路段行程时间以及延误在作为实验结果比较对象时,数据受到测量手段的限制,往往精度不高,导致路段行程时间以及延误作为比较对象缺乏科学性,因而在本次实验无法借鉴。为此,选用小汽车和客车的平均车速作为仿真结果的对比对象。利用最小二乘法,建立以汽车平均车速为因变量,待校正参数为自变量的线性回归方程。本次实验对小汽车车速建立了线性回归方程,公式为

式中:Y为平均行驶车速,X1为最小车头时距,X2为平均停车距离。
通过与调查数据对比,从16组参数组合中选取4组参数,即得到小汽车和大客车的仿真车速与实际车速最为接近的参数组合,然后把各组参数代入方程可得方程估算车速。
以车速误差为2%作为评价标准进行检验,可以发现在模型标定之前,各项输出数据与实际数据的相对误差大小不一,有些误差超过2%,该模型与实际交通状况存在较大的差异,如表4所示。根据建立的回归模型,以回归模型预测结果与实际测量的小汽车与客车行驶速度近似或相等,结合仿真画面的合理性,综合考虑各种检验结果,并将其作为判定标准。模型仿真后最终输出的车速与实际车速基本一致,在小汽车实际车速与仿真车速相对误差中,最大的相对误差仅为1.002%,而客车实际车速与仿真车速相对误差仅为0.341%,均满足2%的要求。其中,第1组、第2组、第3组三组参数组合虽然在小汽车实际车速与仿真车速相对误差上表现较好,但在客车实际车速与仿真车速相对误差,以及小汽车实际车速与估算车速相对误差较大,体现出一定的波动性。而第4组虽然小汽车实际车速与仿真车速相对误差最大,但在其他两个方面的相对误差都较为稳定。最终确定校正值分别为:最小车头时距为4m,平均停车距离为1.5m,即第4组的参数组合最符合要求。
通过再次仿真实验,发现仿真模型最终输出的流量与实际流量相比误差,最大为8.34%,属于可接受的范围(见表5)。这表明该模型满足了模型标定的基本要求,各项输出数据与实际调查数据也基本一致,即初步完成了翔宇大道交通仿真模型的标定,翔宇大道交通仿真模型基本构建完成。

表4 校正参数检验表

表5 流量指标评价结果
4 结束语
本文以淮安市翔宇大道为基础,利用VISSIM软件建立基于翔宇大道的实际交通数据仿真模型,最后,对该模型的参数进行校正。根据测量得到的实际数据,利用拉丁方格法对参数进行标定,最终得到的仿真结果与实际数据差距较小。但试验仅针对城市快速路,而对于城市一般道路上的交通流状态更加复杂,冲突区也更多,要想建立一个与实际混合交通流特性相适应的仿真模型还存在一定的差距,这不仅需要软件开发商对软件后续不断地完善和补充,还需要在接下去的研究中,完善道路交通基础数据的收集和整理工作。总之,将VISSIM类国外交通仿真软件应用于我国具体的交通环境时,必须在符合当地实际交通状况基础上,对交通仿真模型的关键参数进行标定,这样,才能使交通仿真模型符合实际。
[1] 雍安娜,朱海笑,马欣.基于VISSIM仿真的交叉口信号控制优化方法研究[J].交通科技与经济,2015,17(1):73-77.
[2] 邹智军,杨东援.道路交通仿真研究综述[J].交通运输工程学报,2001(2):22-23.
[3] 隽志才.交通系统建模与仿真[M].北京:科学出版社,2011.
[4] 钟邦秀,杨晓光.面向对象微观交通仿真系统的研究与实现[J].系统仿真学报,2002,14(4):418-421.
[5] 孙剑,杨晓光.微观交通仿真模型系统参数校正研究—以VISSIM 的应用为例[J].交通信息与安全,2004,22(3):3-6.
[6] CORSIM User's Manual version1.04[M].Washington,D.C:FHW A ,1998.4.
[7] PTV A G.VISSIM 5.10-03COM Interface Manual.

