混凝土坝裂缝转异诊断方法研究

冯 燕

(江西省抚州市临川区水利局，江西 抚州 344100)

混凝土坝裂缝转异诊断方法研究

冯 燕

(江西省抚州市临川区水利局，江西 抚州 344100)

应用小波理论从裂缝的历史实测数据中提取时效变形，通过对时效变形的分析，判断了裂缝在混凝土坝运行过程中是否发生失稳转异以及失稳转异发生的时间，指出由于裂缝发生了失稳转异，裂缝也就从一种性态过渡到另一种性态，以最后一次转异之后的相对稳定的性态为研究对象，对裂缝的进一步研究具有重要的意义。

裂缝，混凝土坝，转异诊断

1 概述

对于运行多年，经历过各种荷载组合的带缝运行的混凝土坝，其坝体上的裂缝可能因遭受过不利荷载组合等因素而发生过失稳扩展[1-4]。裂缝扩展后，裂缝尖端向结构内部延伸，裂缝长度也发生了变化，因此裂缝的性态也发生了变化，从发生失稳扩展前到失稳扩展后，裂缝从一种性态过渡到另一种性态。如果裂缝监测仍以整个时间序列作为研究对象，那么势必造成研究结果的失真。因此，笔者认为，计算和预测裂缝的临界开度等研究应以裂缝当前的开裂性态为准。

本文首先应用小波理论提取裂缝的时效变形，再通过对裂缝的时效变形进行分析，据此确定裂缝失稳扩展发生的时间。

2 确定最近一次裂缝转异的时间

混凝土坝裂缝开度是一个随时间变化的随机过程，同时是一个长期的发展过程[5,6]，裂缝开度的时间效应特性在一定程度上反映了裂缝开度随时间变化发展的趋势，表征了裂缝失稳转异的特征，因此可以根据裂缝开度的时效变化来研究裂缝的失稳转异。混凝土坝裂缝开度的时效变形主要有三种基本形式：1)裂缝时效变形以不断变小的速率增大并逐渐趋于稳定；2)随运行时间的延长，裂缝时效变形以恒定的速率增大；3)裂缝时效变形以不断增大的速率增大。

运行中的混凝土裂缝，若裂缝开度或裂缝深度随时间变化的趋势为以上第一种基本形式，表明裂缝没有发生失稳转异，即裂缝处于稳定的状态，此时的裂缝对大坝运行安全影响较小；若裂缝开度或裂缝深度随时间变化的趋势为以上第2)，3)种基本形式时，表明裂缝已经发生失稳转异，即裂缝处于非稳定的状态，大坝的工作性态向恶化方向发展，有可能危及大坝的安全。

2.1 裂缝时效变形的小波提取

通过对裂缝的时效变形进行分析，由此而判断裂缝是否发生过失稳转异以及失稳转异发生的时间，在这个过程中，首先必须提取出裂缝的时效变形。以往在确定时效变形时通常采用的方法一般是事先人为选好一定形式的时效因子，将其代入统计模型，在通过用线性最小二乘回归的方法求出回归系数的基础上确定时效分量。该方法不但包含一定的人为因素，而且因子间也会存在较大程度的线性相关，从而导致回归分析的结果变得不准确，分离出的时效变得不可靠。为了提取裂缝的时效变形，利用小波理论来对裂缝实测数据进行分析，进而提取时效变形。

在混凝土坝裂缝开度数据的小波分析中[7]，所采用的小波母函数Ψ(t)是一个平方可积函数，并且满足如下的允许条件：

(1)

将小波母函数Ψ(t)进行伸缩和平移后，就得到小波基函数：

(2)

其中，a为尺度因子；b为位移因子。

对一个信号f(t)的小波变换即为：

(3)

其中，<·，·>为内积。

可将混凝土坝裂缝开度实测数据作为实测信号，用小波变换对裂缝开度的实测数据进行分析。在式(3)所示的连续小波变换中，尺度因子a和位移因子b是连续变化的，但在混凝土坝裂缝开度实测数据小波分析的实际应用当中不可能对尺度因子a和位移因子b的所有取值都进行计算，因此需要对尺度因子和位移因子的取值按照一定方式进行离散小波变换，其离散化处理过程为：

此时Ψa,b(t)变为：

(4)

在混凝土坝裂缝开度实测数据小波分析的实际当中可取a0=2，b0=1，此时，Ψa,b(t)变为：

Ψj,k(t)=2-j/2Ψ(2-jt-k)

(5)

对实测信号f(t)的离散小波变换即为：

(6)

函数Ψj,k(t)=2-j/2Ψ(2-jt-k)在不同尺度j下，随着k的变化，形成了不同的尺度空间{Vj}j∈Z。若子空间Wj+1与尺度空间Vj和Vj+1之间满足如下关系：

Vj=Wj+1⨁Vj+1Wj+1⊥Vj+1

(7)

则Wj+1为Vj的正交补空间，则有：

V0=W1⨁V1=W1⨁W2⨁V2=W1⨁…⨁Wj⨁Vj

(8)

也就是说，空间V0可以用有限个子空间来逼近。

混凝土坝裂缝监测数据是一个实测数字信号，设其在V0上的投影为S，根据V0=W1⨁V1，信号在V1上的投影为其低频部分，记为A1，在W1上的投影为其高频部分，记为D1。根据Vj-1=Wj⨁Vj，信号在Vi上的投影为Aj，为其低频，在Wi上的投影为Dj，为其高频。由此可以将信号逐级分解，如图1所示。

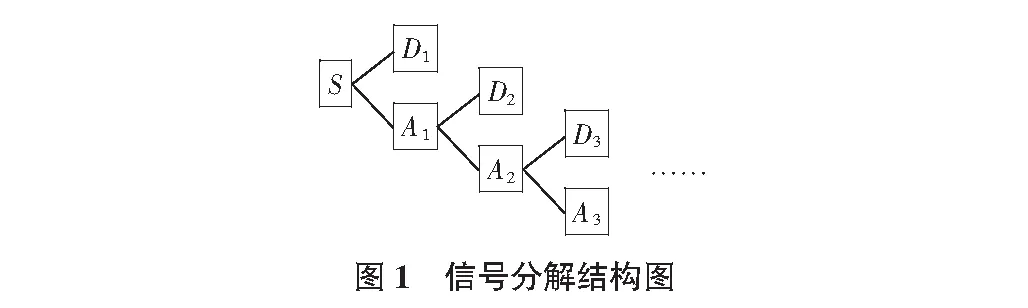
运行期混凝土坝裂缝开度变化的影响因素可以归结为水压、温度和时效三个主要部分，而实际测得的裂缝开度数据中还会夹杂有一定的观测误差。裂缝开度实测值序列可以看成一系列的数字信号，该数字信号由不同频率的信号成分组成。其中，受随机因素或者观测误差影响的部分表现为高频信号，受水位和温度因素影响的部分表现为明显周期性变化规律，亦表现为高频信号，而裂缝时效变形部分则表现为低频率信号，因此，根据三个不同组成部分数字信号频率的表现不同，用小波方法对裂缝开度测值序列进行分解，高频率部分，剩下的低频部分就代表着裂缝测值序列的发展趋势，即为裂缝的时效变形。

2.2 裂缝时效转异点的识别

裂缝开度的时效变化是裂缝系统发展演变的表征，反映了裂缝在各种影响因素作用下的演变情况。对裂缝开度的时效变化进行分析，可以了解裂缝的发展演化规律，分析裂缝的失稳转异情况。

本文根据裂缝开度时效的大小、变化的速率以及加速度等变化特征来分析混凝土坝裂缝的演变规律，判别裂缝的转异情况。混凝土裂缝的时效变形包括裂缝尖端的塑性变形、混凝土自身体积变形以及混凝土徐变等，可以用一阶非线性微分方程表示：

(9)

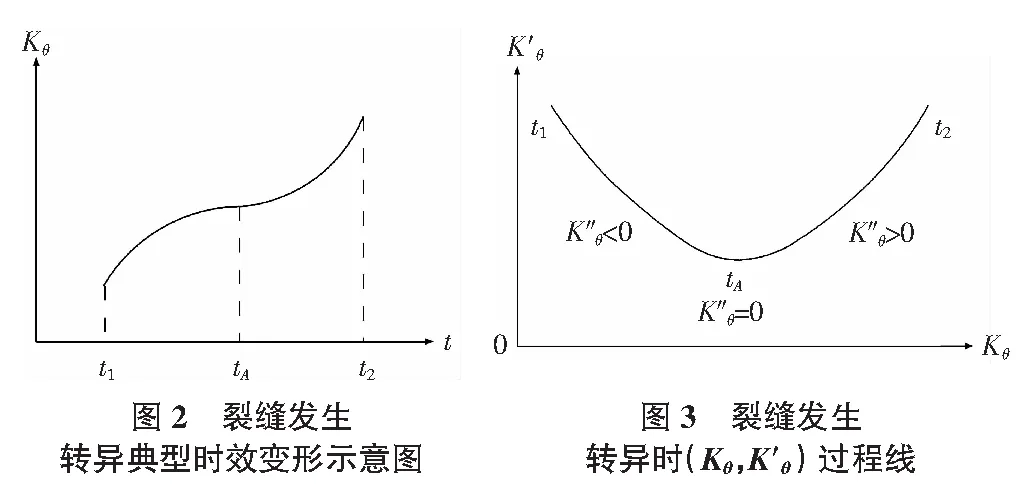
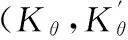
在本文研究过程中，重点考察裂缝时效的变化速率以及加速度来建立判断准则，其时效转异点判断准则为：

(10)

根据以上对裂缝时效进行的分析，可以判断出裂缝在运行过程中是否发生过失稳转异以及失稳转异发生的时间。由于裂缝失稳转异后性态发生变化，因此应根据裂缝最后一次失稳转异时间以后的开度实测数据来拟定裂缝当前状态下的警戒值。下面重点研究裂缝开度警戒值的拟定过程。

3 实例分析

以某混凝土重力拱坝为例，该坝坝顶高程126.3 m，最大坝高76.3 m，自左向右共分为28个坝段。大坝设计洪水位122.2 m，校核洪水位124.6 m，保坝水位127.7 m，正常蓄水位119.0 m，汛期限制水位117.0 m。水库总库容为28.25亿m3，为多年调节水库。主要监测项目有：平面网、高程网、沉陷观测、正倒垂线、扬压力、绕坝渗流、内部仪器、水质分析等九项。其中，垂线、水位、气温、裂缝和接缝、库水温以及混凝土温度观测项目共109个测点已实现自动化观测。

以下游面105 m高程裂缝测点18-Ⅰ 为例，取1979年—2007年约28年的裂缝开度实测值，过程线见图4。

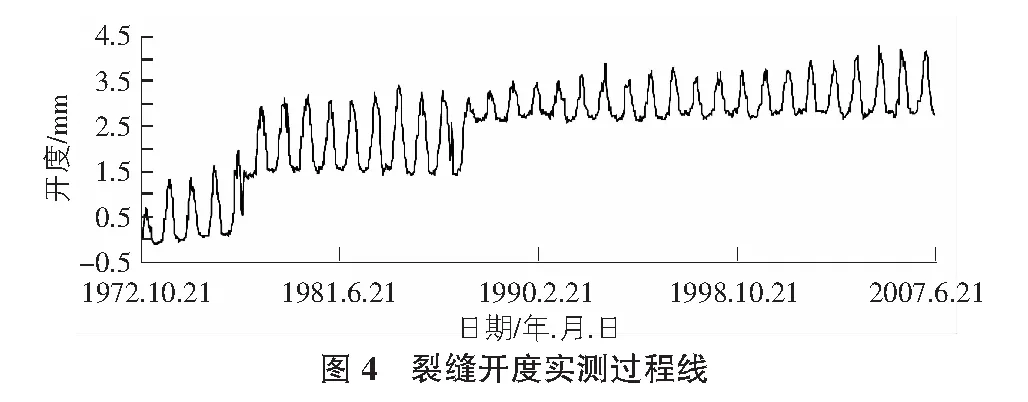
对裂缝开度实测数据进行小波分析，滤去其分解得到的高频部分，剩下的低频部分作为裂缝开度变化的时效，提取出的时效变化过程线如图5所示。

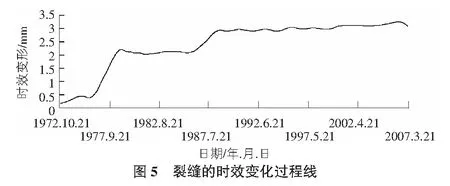
从图4中可以看出该裂缝的开度在1976年—1978年间和1987年分别经历了两个突然性的变化阶段，在小波分析提取出的时效变形过程线上也明显地反映出这两个突然性的变化。

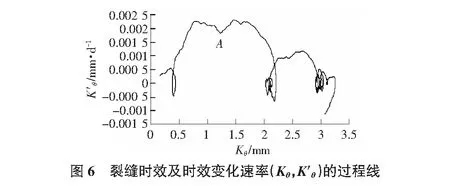
从图6中可以看出，曲线在A点处出现拐点，且在A点附近曲线的变化特征与图3所示的裂缝发生失稳转异的典型变化特征相似，因此可以确定A点即为裂缝的时效失稳转异点，失稳转异的时间发生在1977年4月，从对应的实测资料序列可以看出，1977年4月大坝的裂缝开度突然增大，究其原因，该混凝土坝于1976年7月经历了高温低水位，同年年底—1977年年初又经历了低温低水位，1977年底—1978年初再次经历低温低水位，1978年7月，再次经历高温低水位，同年底至1979年年初第三次经历低温低水位。从以上分析可知，1976年—1979年期间遭遇了两次高温低水位和三次低温低水位的袭击，使得该坝裂缝在1976年底—1977年初发生了不可逆的变化，也就是说裂缝在此阶段发生了转异。

此外，从实测过程线上还可以看出，在1987年裂缝开度也发生了显著的变化，裂缝开度的年最小值有所增大，但是年最大值却改变不太明显，究其原因，该混凝土坝在1987年初对裂缝进行了环氧灌浆，由于裂缝年最大值变化不大，因此，不认为裂缝在此时刻发生了失稳转异。

4 结语

本文重点研究了混凝土坝裂缝转异诊断的方法，以裂缝的时效变形为依据研究裂缝的失稳转异，首先从裂缝的历史实测数据中提取裂缝的时效变形，进而对裂缝的时效变形进行分析，据此判断裂缝在以往的运行过程中是否发生过失稳转异以及失稳转异发生的时间。由于裂缝的转异失稳，裂缝也从一种性态过渡到另一种性态。以最后一次转异之后相对稳定的性态为研究对象，将对裂缝的进一步研究具有重要的意义。

[1] 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社，2006.

[2] 吴中如，沈长松，阮焕祥.水工建筑物安全监控理论及其应用[M].南京:河海大学出版社，1990.

[3] 景 继.混凝土坝裂缝开度预测及警戒值拟定方法研究[D].南京:河海大学，2010.

[4] 张焕敏，涂兴怀.水工混凝土裂缝的成因及控制[J].混凝土，2005(10):73-76.

[5] 朱伯芳.混凝土拱坝运行期裂缝与永久保温[J].水力发电，2006(8):21-24.

[6] 黎展眉.普定碾压混凝土拱坝裂缝成因探讨[J].水力发电学报，2001(1):96-102.

[7] 徐洪钟，吴中如，李雪红，等.基于小波分析的大坝观测数据异常值检测[J].水电能源科学，2002(4):20-21.

The research of concrete dam crack abnormal diagnosis

Feng Yan

(JiangxiFuzhouLinchuanBureauofWaterResources,Fuzhou344100,China)

Based on the wavelet theory, the paper extracts the aging deformation of historical recorded data of concrete cracks and judges whether the concrete cracks turn abnormal and the relevant occurrence time during the operation of concrete dam. It is turned out that, under the function of instability of concrete cracks, the cracks transfer from one state to another. By taking the relatively stable state as the research object after the last abnormal variation would be of certain significance for the future research.

crack， concrete dam， abnormality diagnosis

1009-6825(2015)32-0217-03

2015-08-20

冯 燕(1970- )，女，工程师

TV642

A