Eshelby夹杂理论在岩石力学中的应用探讨★

陈 晓 黄思婷

(1.解放军理工大学国防工程学院爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;2.江苏省南京市长江都市建筑设计院，江苏 南京 210002)

Eshelby夹杂理论在岩石力学中的应用探讨★

陈 晓1黄思婷2

(1.解放军理工大学国防工程学院爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;2.江苏省南京市长江都市建筑设计院，江苏 南京 210002)

根据夹杂理论在复合材料方面的应用及岩石自身特性，初步分析了Eshelby等效夹杂理论在分析岩石宏观弹性模量、岩石流变以及工程实际等方面的应用，并探讨了理论应用过程中孔隙弹性的处理方法，以供参考。

Eshelby等效夹杂，复合材料，岩石流变，孔隙弹性

0 引言

近些年来，岩石力学有了突飞猛进的发展。一方面，随着近些年人类对能源需求越来越高，人们逐渐将注意力转移到更深部储藏的丰富矿产。另一方面，人们也着力对一些重要的稀有资源进行储备和储藏，这就要求人们对深部岩体的力学性能，尤其是对高温高压、含矿物质、孔隙水等因素岩体有一个更深入的了解。在此基础上发展起来的深部开采工程力学就主要针对深部资源开采过程中而引发的与巷道工程及采场工程有关的岩石力学问题等进行研究，这些问题的解决对于防止开采过程中发生重大事故，提高经济效益等具有重要意义[1]。

在岩石力学发展初期，岩石被看作连续介质，弹塑性理论是它的理论基础。随后，针对岩体结构低刚度不连续面的研究，岩石逐渐被看作不连续介质进行研究[2]。目前，随着CT等技术的应用，人们对岩石内部结构有了更为直观的认识，同时，岩石及孔隙流体流固耦合效应的研究得到广泛发展[3,4]。岩石由于其构成的复杂性，目前对岩石细观力学方面的研究尤其是深部岩体力学特性仍在不断深入。工程实践已经表明，单凭经验进行判断往往越来越难以适应日益发展的工程规模和工程复杂性[5]，因此，在成熟经验的基础上，利用细观力学方法在复合材料等方面取得的应用成果，结合构成相对复杂岩石自身特性对力学行为研究有重要意义，本文将对Eshelby等效夹杂理论在岩石力学可应用问题可行性进行探讨。

1 Eshelby等效夹杂理论应用于岩石力学可行性分析

Eshelby等效夹杂理论是研究细观力学的基础方法，Eshelby利用三维弹性问题的Green函数方法，给出了椭球夹杂问题的显式解，并对夹杂周围弹性应力场进行了分析[6,7]。国内外对此开展了广泛的研究，研究成果推动了复合材料力学、含杂质钢材力学等的研究和裂纹位错等问题的分析，具有很好的适应性。

1.1 Eshelby等效夹杂理论在研究岩石宏观弹性模量的应用

梁军，杜善义[8]应用Eshelby等效夹杂理论研究了复合材料的弹塑性问题，并研究了多轴荷载下复合材料弹塑性应力—应变关系问题。韩佳[9]针对Eshelby解的平均场方法高估复合材料弹塑性模量的问题，采用新的确定Eshelby张量的方法，结合Mori-Tanaka方法建立了颗粒增强弹塑性基体复合材料力学特性的评估方法。胡敏等[10]采用Eshelby张量和Mori-Tanaka等效方法，将含卵石砂土，通过替换迭代的方式，研究了求解其宏观等效弹性模量的方法。

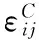
(1)

其中，Sijmn为只与夹杂形状和基体泊松比有关的常数张量，称为Eshelby张量。上述公式建立了外力作用下，基体与“夹杂”弹性关系的基础，此关系对于理想化的岩石单元也是成立的，但针对岩石体内的流体处理为“夹杂单元”或“高压孔隙单元”，需要确定能够定性描述“夹杂单元”内部孔隙弹性模量。这样，就能够建立基于“孔隙弹性模量”的岩石弹性性质与岩石围压、孔隙度、含水率之间的关系方程。

1.2 Eshelby等效夹杂理论在研究岩石流变的应用

岩石的长期强度和稳定性分析是岩石力学未来发展的重要方向[11]。Eshelby等效夹杂理论在研究复合材料流变方面也有广泛的应用，在式(1)的基础上，根据弹性—粘弹性等效原理，得到含夹杂弹性岩样弹性模量即含球形粘弹性材料在象空间的有效弹性模量；基于如下关系[11]：

(2)

1.3 Eshelby等效夹杂理论在加固工程的应用

矿产资源开采过程中易多发事故，而针对破碎岩体注浆加固等工程措施非常必要。而复合材料中针对不同夹杂类型与基体力学特性已经深入微观层次，王治[12]建立了细观力学中压电材料的修正广义Eshelby张量，并建立了夹杂与基体为非完美界面时的三维细观力学框架。这些理论有助于解释岩石基体与孔隙的相互作用中考虑孔隙内浆液流体和岩石基体接触面耦合作用，并在此基础可以结合不同注浆材料对注浆效果的不同，在工程实践中改进破碎岩体注浆实践效果，对于一些重要军事目标和民用经济目标改进防护措施，具有重要的参考意义。

2 基于Eshelby等效夹杂理论岩石孔隙弹性分析

在岩石力学中应用Eshelby等效夹杂理论需要充分考虑岩石自身特性与复合材料力学行为的相同与区别，同时，岩石基体由于其构成复杂，受各类切割面等因素的影响，均值化过程中需要考虑多方面的影响。同时，孔隙的弹性建模不仅要考虑孔隙内流体弹性模量作用，也要考虑周围基体对孔隙弹性的影响[13]。孔隙内流体弹性在变化比较小的情况下流体弹性状态满足以下条件：

(3)

式(3)反映了孔隙内流体压缩性β、孔隙体积V、体积内压强p之间的关系。同时，成熟的模拟孔隙弹性的夹杂模型应充分考虑微观结构上孔隙渗流特性，能够充分反映在外力作用下，岩石孔隙对岩石整体力学行为的影响。

3 结语

本文结合岩石力学的发展过程，针对目前深部复杂环境岩体力学特性理论研究方面存在的问题，提出在成熟经验基础之上，结合岩石自身特性，分析了Eshelby等效夹杂理论在研究岩石宏观等效弹性模量、岩石流变以及加固工程等方面的应用，并针对理论应用就岩石的孔隙弹性描述方法进行了分析，具有较好的实用性。同时，随着人们对材料细观结构研究的不断深入，Eshelby夹杂理论也在不断发展，在实践中的广泛应用又进一步促进了理论的发展。同样，随着在深部岩体工程实践中不断发现的新问题，需要更新的理论对推进实践进行支撑，同时，应充分认清岩体结构的复杂性，在理论应用过程中充分考虑岩石自身特性，确保理论模型的适用性。

[1] 何满潮.深部开采工程岩石力学现状及其展望[A].第八次全国岩石力学与工程学术大会论文集[C].2004.

[2] 陈宗基,傅冰骏.岩石力学的发展方向[J].岩石力学与工程学报,1990(3):175-183.

[3] 蔺丽君.孔隙尺度渗流及其与变形耦合的细观数值模拟研究[D].成都:西南石油大学,2012.

[4] 程 伟.储层微观结构的随机模型及其渗流规律的数值模拟[D].武汉:武汉工业大学,2012.

[5] 刘世安,宋仕兵.试论我国岩石力学的研究现状与发展动向[J].西部探矿工程,2013(2):161-163.

[6] Eshelby,J.D. The determination of the elastic field of an ellipsoidal inclusion and related problems, Proc. Roy. Soc. Lond.A,1957(241):376-396.

[7] Eshelby,J.D. The elastic field outside an ellipsoidal inclusion, Proc. Roy. Soc. Lond.A,1959(252):561-569.

[8] 梁 军,杜善义.弹塑性复合材料力学性能的细观研究[J].固体力学学报,2000,12(4):361-365.

[9] 韩 佳.基于Mori-Tanaka方法的颗粒增强弹塑性基体复合材料力学特性研究[D].重庆：重庆大学,2014.

[10] 胡 敏,徐国元,胡盛斌.基于Eshelby张量和Mori-Tanaka等效方法的砂卵石土等效弹性模量研究[J].2013,34(5):1437-1442.

[11] 吴 俊，杨新华，叶 永.基于Eshelby等效夹杂理论的沥青混合料有效粘弹性质分析[J].工程力学，2012(10)：244-248.

[12] 王 治.水泥基压电复合材料的模拟与优化设计[D].杭州：浙江大学，2014.

[13] 史 謌,杨东全,杨慧珠.岩石的孔隙弹性研究[J].北京大学学报(自然科学版),2000,36(2):214-220.

The application of Eshelby’s theory on rock mechanics discussion★

Chen Xiao1Huang Siting2

(1.StateKeyLaboratoryofExplosiveImpactandDisasterPrevention,InstituteofNationalDefenseEngineering,PLAUniversityofScienceandTechnology,Nanjing210007，China;2.NanjingYangtzeRiverUrbanArchitecturalDesignInstitute,Nanjing210002,China)

This paper combine the use of Eshelby’s theory on composite material and the features of rock mass, analyzing the feasibility of Eshelby’s theory on rock mass’s macroscopic elastic modulus, rock rheology, engineering application， explores the treatment of porous elastic in the theoretic application, so as to provide some reference.

Eshelby’s theory, composite material, rock rheology, pore elasticity

1009-6825(2015)32-0063-03

2015-09-01★：江苏省自然科学基金(项目编号：BK20141067)

陈 晓(1992- )，男，在读硕士； 黄思婷(1991- )，女，助理工程师

TU452

A