基于非合作博弈模型的量子蚁群算法

甘泉，王启明，时合生

基于非合作博弈模型的量子蚁群算法

甘泉，王启明，时合生

针对量子蚁群算法求解组合优化问题时易陷入局部最优和收敛速度慢的问题，提出一种基于非合作博弈模型的量子蚁群算法（quantum ant colony algorithm based on non-cooperative game theory，NGQACA），采用重复博弈模型，在重复博弈中产生一个博弈序列，使得每次博弈都能够产生最大效益，并得到了相应博弈过程的纳什均衡。利用三个典型的标准测试函数对此算法进行实验测试，实验结果表明本文基于非合作博弈模型的量子蚁群算法的收敛精度和稳定性均要优于量子蚁群算法（quantum ant colony algorithm，QACA）和蚁群算法(ant colony algorithm，ACA)。

非合作；博弈论；蚁群算法；位置变异；函数分析

0 引言

博弈论的最大特点是能够为相应的博弈过程找到纳什均衡点，而纳什均衡点也正是策略的最优点[1]。非合作博弈经常用于分析解决这种问题并且纳什均衡解被认为是这种博弈的解[2-3]。即使非合作博弈模型的主要目的是为了最大化所有次级用户的收益，根据所有次级用户采取的均衡解，主用户的收入也同样会被最大化[4-7]。针对量子蚁群算法求解问题的不足，根据博弈论的思想，本文提出一种基于非合作博弈模型的量子蚁群算法，采用重复博弈模型，在重复博弈中产生一个博弈序列，使得每次博弈都能够产生最大效益，并得到了相应博弈过程的纳什均衡。该算法设计扩大解的搜索空间，改善种群信息结构，避免搜索陷入局部最优。并将该算法与目前比较常用的一些算法进行了比较，结果表明该算法具有更好的收敛速度。

1 量子蚁群算法

量子蚁群算法是基于量子计算原理的一种蚁群算法，将量子计算与蚁群算法相结合的量子蚁群算法是一种崭新的优化方法，具有很强的生命力和研究价值[8]。

A.Narayanan&M.Moore在“Quantum-ant algorithm”一文中提出了量子蚁群的概念，并将量子蚁群算法用于求解组合优化问题，取得了较好的效果[9]。M．Dorigo曾给出三种不同模型，分别称之为蚂蚁循环系统（ant-cyclc system）、蚂蚁数量系统（ant-quantity system）、蚂蚁密度系统（ant-density system）[10-15]。它们的差别在于公式的不同，在蚂蚁数量系统模型中如公式（1）：

这3种模型的区别在于后两种模型中利用的是局部信息，而前者利用的是全局信息，经过实验对比，在求解问题时蚂蚁循环系统性能较好，因而本文采用它作为基本模型。算法停止条件可以用固定循环次数或者当解的变化不明显时便停止计算。

基本蚁群算法实现步骤如下：

（1）初始化

（2）迭代过程

根据公式（1）和（2），蚂蚁k选择下一个地点j，将蚂蚁k移动到城市j，把城市j置入禁忌列表tabak；

计算所有蚂蚁求得的回路距离，根据公式（1）、（2）更新路径(i,j)上的信息激素；

（3）输出结果，结束算法。

2 非合作博弈模型

2.1 非合作博弈模型

为不失一般性，本文以求函数的最小值为例，始终成立如公式（3）：

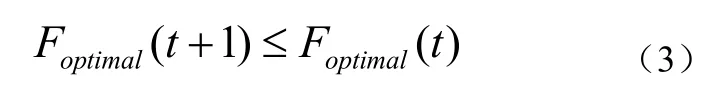
其中t为迭代次数，F为最优值的函数。非合作博弈理论中，参与者只根据他们的可察觉的自我利益（perceived self-interest）来决策。参与者之间的威胁、协议、许诺之类，是无法实施的，即便参与者在博弈中可以相互沟通。除了那些博弈规则确实允许的协议外，参与者无法达成有约束力的协议。对于一个两只蚂蚁博弈模型而言，分别用“0”和“1”代替两个博弈方，当“0”首先进行策略选择时，它会选择使自己的收益尽可能大的策略，然后“1”可根据自身收益来考虑是接受还是拒绝由“1”提出的策略，如果1不受益，1就不接受，如果1受益，1就接受，并且1自动获得下一轮的优先选择权。

2.2 初始种群产生

在NGQACA中，采用编码方案如公式（4）：

qi0为|0＞态位置,qi1为|1＞态位置。

3 位置变异处理

3.1 蚂蚁位置变异处理

本文基于博弈模型的改进算法使用一种通过量子非门设计的变异操作，具体步骤如下：（1）以概率Qm从量子蚂蚁种群中选取若干个个体；（2）对选中的量子蚂蚁个体按概率Pm确定一个或多个变异位；

（3）对选中位量子比特的几率执行量子非门操作。3.2最优位置更新规则

设蚂蚁Pi当前搜索到的最优位置如公式（7）：

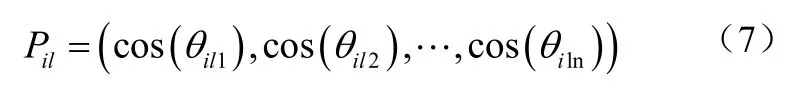
整个种群目前搜索到的最优位置如公式（8）：

位置状态更新规则描述为：

（1）蚂蚁Pi上量子位幅角增量的更新如公式（9）：

（2）蚂蚁上量子位概率幅的更新如公式（10）：

蚂蚁Pi更新后的两个新位置如公式（11）、（12）：

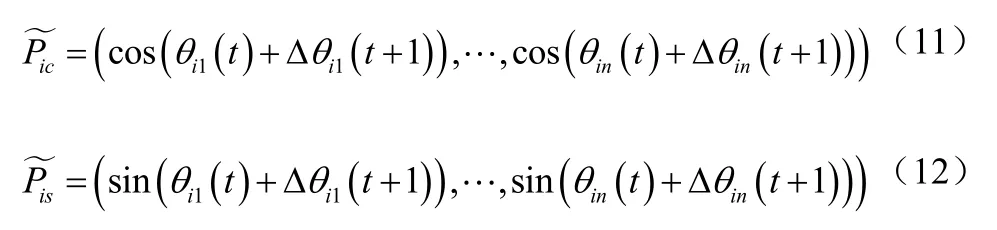
4 仿真实验结果与分析

为验证本文算法的有效性以及可行性，本文利用3个典型的标准测试函数对NGQACA算法寻优性能进行测试。对每个测试函数分别进行测试；测试函数（1）主要测试算法陷入局部最优的问题。实验采用测试函数（2）Rosenbrock函数以及测试函数（3）Bohachevsky函数进行优化，寻找函数极值来测试算法在时间上的优越性[16-18]。

测试函数（1）

测试函数（2）Rosenbrock函数：

首先对测试函数进行测试，将GQACA测试结果与文献[5]中报道的NQACA和基准的ACA的结果进行比较。进化曲线如图1，图2所示：

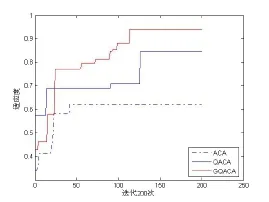
图1 函数f(1)的寻优曲线（迭代200）

图2 函数f(1)的寻优曲线（迭代500）

从图表中列出结果可以看出，本文NGQACA算法的收敛精度和稳定性均要优于QACA算法和ACA算法,并且能较好的避免陷入局部最优。

Rosenbrock函数存在2个极大值点3897.7342和3905.9262，Bohachevsky函数有多个局部极大值，全局极大值为0.24003441。两种算法个体数量均为40，最大迭代次数200，实验次数50，优化结果如表1所示：

表1 三种算法优化结果比较

由此可见GQACA明显优于QACA以及ACA。

5 总结

提出一种新的基于博弈论的量子蚁群算法。采用重复博弈模型，在重复博弈中存在一个博弈序列，每次博弈都能够产生最大效益。并得到了相应博弈过程的纳什均衡。利用典型的标准测试函数对NGQACA算法寻优性能进行测试。实验结果表明本文NGQACA算法的收敛精度和稳定性均要优于QACA算法和ACA算法。

[1]P.Li and S.Li,"Quantum ant colony algorithm for continuous space optimization,"[J].Control Theory and Applications,2008,25(2):237-241.

[2]P.C.Li and H.Y.Wang,"Quantum Ant Colony Optimization Algorithm Based on Bloch Spherical Search,"[J].Neural Network World,2012,22(4):325-341.

[3]袁浩.基于量子蚁群算法的粗糙集属性约简方法[J].计算机工程与科学,2010,32(5):82-84.

[4]P.Li,K.Song,and E.Yang,"Quantum ant colony optimization with application,"2010 Sixth International Conference on Natural Computation[C].(ICNC),2010:2989-2993.

[5]W.Honggang,M.Liang,Z.Huizhen,etal. Quantum-inspired ant algorithm for knapsack problems [J].Journal of Systems Engineering and Electronics,2009,20(5):1012-1016.

[6]许波.彭志平,余建平,等.基于蛙跳思想的量子编码遗传算法[J].中国工程科学,2014,16(3):113-117.

[7]沈鹏.物流配送路径优化问题求解的量子蚁群算法[J].计算机工程与应用,2013,49(21):56-59.

[8]贾瑞玉,李亚龙,管玉勇.求解旅行商问题的混合量子蚁群算法[J].计算机工程与应用,2013,49(22):36-39.

[9]何小锋,马良.求解0-1背包问题的量子蚁群算法[J].计算机工程与应用,2011,47(16):29-31.

[10]Chandra Mohan B,Baskaran R.A survey:Ant Colony Optimization based recent research and implementation on several engineering domain[J].Expert Systems with Applications,2012,39(4):4618-4627.

[11]田有亮,马建峰,彭长根,等.秘密共享体制的博弈论分析[J].电子学报,2011,39(12):2790-2795

[12]曾晓丽,胡伟,曹海,等.基于博弈论的多媒体传感器网络MAC协议[J].计算机工程,2013,39(6):103-106.

[13]刘玉岭,冯登国,吴丽辉,等.基于静态贝叶斯博弈的蠕虫攻防策略绩效评估[J].软件学报,2012,23(3):712-723.

[14]Dorigo.M．Optimization,learning and natural algorithms [D].Ph.D.Thesis,Department of Electronics,Politecnico di Milano,Italy,1992.

[15]Maniezzo V,Dorigo M,Colorni A.．The ant system：optimization by a colony of cooperating agents[J]．IEEE Transactions on Systems，Man，and Cybernetics-Part B.1996,26(1):29-41.

[16]Diosan L,Oltean M..What Else is the Evolution of PSO Telling Us[J].Journal of Artificial Evolution and Applications,2008,8(2):1-12.

Quantum Ant Colony Algorithm Based on Non-cooperative Game Theory

Gan Quan,Wang Qiming,Shi Hesheng
(School of Computer Science and Technology Department,Pingdingshan University,Pingdingshan 467002,China)

Quantum ant colony algorithm is easy to fall into the situation of local optimum and slow convergence rate when solving combinatorial optimization problem.This paper puts forward a quantum ant colony algorithm based on non-cooperative game theory(NGQACA).Adopted in this algorithm,the repeated game model can produce a game sequence to make every game produce maximum benefit,and then it can get the corresponding game process of Nash equilibrium.The there typical test functions are used for testing the performance of NGQACA algorithm optimization.The experimental results show that the convergence precision and stability of NGQACA are better than QACA and ACA algorithm.

Non-cooperative;Game Theory;Ant ColonyAlgorithm;Position Variation FunctionAnalysis

TP393

A

1007-757X(2015)06-0026-03

2015.03.04）

甘 泉（1980-），男，安徽省灵璧县，平顶山学院，计算机科学与技术学院，讲师，硕士，研究方向：算法分析，平顶山，467000

王启明（1980-），男，鲁山人，平顶山学院，计算机科学与技术学院，讲师，硕士，研究方向：软件工程算法，平顶山，467000

时合生（1977-），男，郾城县人，平顶山学院，计算机科学与技术学院，讲师，硕士，研究方向：计算机软件与理论，平顶山，467000