BIM中基于蒙特卡罗模拟的成本估算的研究

赵倩纯，胡伟松，吴百锋

BIM中基于蒙特卡罗模拟的成本估算的研究

赵倩纯，胡伟松，吴百锋

近年来，建筑信息模型（Building Information Model）成为建筑领域的一项重要技术，代表着建筑设计技术的一个方向。基于BIM技术的建筑成本估算是其中的一个重要环节，但由于这种估算难度大，受到的风险因素多，一般的分析方法难以充分地纳入各种影响因素，影响了评估的客观准确性。蒙特卡罗模拟方法是研究这类有众多复杂影响因素的分析过程的强有力工具，但庞大的计算量影响了其应用。基于现代众核处理机体系结构，将蒙特卡罗模拟过程设计为一个大规模数据级并行计算，使得庞大的计算量可通过处理机核的数量的增加而化解，不再成为应用中的障碍。实验结果验证了计算过程理想的并行性和可扩展性。

BIM；成本估算；蒙特卡罗；数据级并行；可扩展性

0 引言

建筑信息模型BIM，是以建筑工程项目的各项信息数据作为基础建立的模型，如设计、施工、运营过程中的相关数据[1-2]。BIM通过数字信息仿真模拟建筑物的真实信息，代表着建筑信息化的发展方向。利用BIM技术，可以实现碰撞检测、能耗分析、成本预测，还可以实现虚拟设计和智能设计等[2]。其中，作为BIM技术的重要组成部分，建筑领域成本估算在节约成本、降低风险等方面具有重要意义。

和一般的产品生产过程不同，建筑项目的实现过程是在复杂的外部环境和条件下进行的，往往受到诸如自然、劳动生产率、施工管理水平、市场等众多不确定的风险因素的影响，而且这些风险因素之间相互联系互相影响。传统的成本分析方法根据各成本构成要素进行简单的求和计算，不能充分考虑各风险因素的影响，人为地忽略掉影响因素带来的不确定性和复杂性，因而难以获得具有可信度的准确成本值。

蒙特卡罗方法是研究复杂系统以及不确定过程的强有力的工具[3]。蒙特卡罗方法是以研究对象的概率特征和随机分布为依据，进行数学建模和随机数采样，通过对样本的多次独立重复的模拟试验，获得问题的近似解。只有模拟试验次数足够多，求得的结果才能十分接近精确值。比如，使用蒙特卡罗方法估算圆周率π的值，放置30000个随机点后，π的估计值与真实值仍然相差0.07%。因此，为了满足计算结果的高精度和高准确度，蒙特卡罗模拟将涉及到庞大的计算量，这对硬件平台的能力提出了很高的要求，使得传统的多处理器系统难以胜任。

从本质上将，蒙特卡罗模拟包含多次独立重复试验，而且每次试验都是相互独立的，彼此之间没有数据依赖关系，具有天生的并行性。拥有成千上万个处理核心的的新型众核处理机的问世，为这类蒙特卡罗模拟应用提供了一种新的解决途径。在本文中，我们设计了面向众核体系结构的蒙特卡罗模拟估算方法，启动众多并行线程，由各处理器核心同时执行，每个线程处理一部分数据。这样每个线程实际上处理的数据量是非常少的，庞大的计算量通过处理机核数的增加得以化解。

1 成本估算模型

1.1 传统计算方法及其局限性

建筑项目的成本的基本计算公式如公式（1）：

其中Q表示工程量，S表示人工费、R表示材料费、F表示设备机械费、M表示管理费、P表示利润、C表示规费、T表示税金。

在实际项目实施过程中，所发生的活动及结果具有一定的不确定性，这类不确定性的影响使得各种要素之间并不是独立的，比如当工程量发生变化时，人工费、材料费、管理费等也有会相应的变化，而传统的估算方法忽略了各成本构成要素彼此之间的关联性。传统的方法是根据设计图纸以及定额或者经验数据，将各成本构成要素进行简单的加和计算，从而计算出一个总的确定的数值作为建筑项目总的成本值，这是一种确定性的计算方法。实际上，工程项目的各成本构成要素具有较大的不确定性，并非是能事先确定的定值，而是服从某种概率分布的随机变量，传统的估算方法显然忽略掉了工程项目成本要素的不确定性。

1.2 成本估算模型介绍

如图1所示：

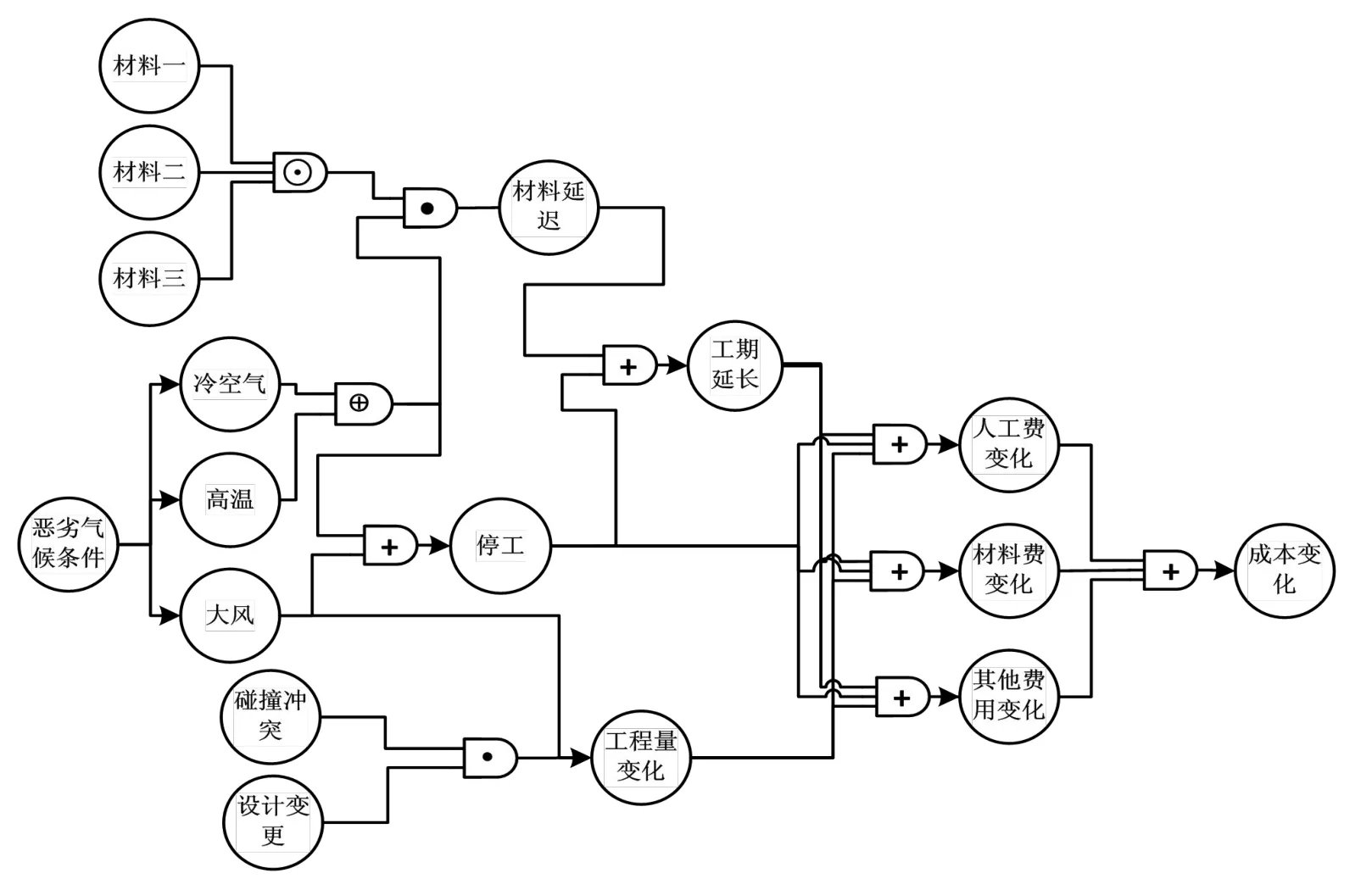
图1 成本模型举例

我们的成本模型以材料选择延迟、恶劣天气、解决碰撞冲突的设计变更这3个事件为例，来分析有关活动对项目成本的影响。图1中各个逻辑关系符号及其表达的含义如表1所示：

表1 逻辑符号与相关含义

从图1的模型中可以看出，建筑项目设计施工过程中往往受到众多活动的影响，这些活动之间还存在着复杂的关联关系。各种活动的作用使得每个构成要素的值并不是固定的，这种影响程度的可变性难以用数字准确地表示。在各种随机因素的共同作用下，各个构成要素的值分布在一个区间内，在此区间内的分布也不一定是均匀的，并且存在着一个近似的、最可能的值。在进行大量的模拟后，它们会呈现出一定的规律性，服从某种统计分布，可以用数学的方法对它们的分布情况加以描述。虽然不可能确切地知道该值，但可以依据工程项目的历史成本资料，考虑时间因素，计算出成本模型中各活动的分布参数，并用蒙特卡罗方法逐步模拟出项目的各构成要素的可能成本区间，进而得出一个比较精确的、近似的成本值。

2 蒙特卡罗模拟

蒙特卡罗（Monte Carlo，MC）方法是一种数值计算方法，应用随机数来进行计算机模拟，在1947年由N·Metropolis命名，并于1949年正式使用[5]。此方法对研究的系统进行随机抽样，通过对样本值的观察统计，求得所研究系统的某些参数，因此也称为随机模拟（Random Simulation）法或随机抽样（Random Sampling）法。

2.1 蒙特卡罗模拟的基本原理

蒙特卡罗模拟方法的基本思想为：当所求问题的解是某个事件的概率或者某个随机变量的数学期望时，通过某种试验的方法，得出该事件发生的频率或者该随机变量，通过求若干个具体观察值的算术平均值而得到问题的解。因此，可以将蒙特卡罗方法一般地理解为用随机试验的方法计算积分。也就是说，将所要计算的积分看作服从某种分布密度函数的随机变量的数学期望。

蒙特卡罗模拟法的基本思路是先构造一个概率空间，并在该概率空间中选取一个随机变量r，设随机变量的分布函数为f（r），其统计量为g（r）。根据随机变量的相应分布特征，产生n个随机数，计算相应的统计函数值，则g（r）的算术平均值可以表示为公式（2）：

若r为离散型随机变量，我们用P（g（ri）表示值g（ri）在g（r1）,g（r2）,…g（rn）这个序列中出现的概率，μi表示g（ri）在这个序列中出现的次数，根据伯努利大数定理，对于任意正数ε＞0，极限表达式成立为公式（3）：

则g（r）的数学期望可表示为公式（4）：

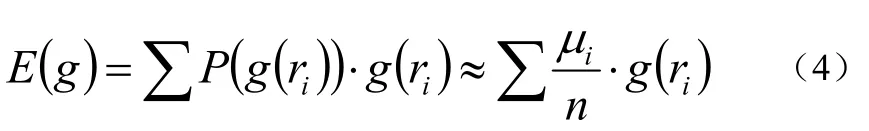
g（r1）,g（r2）,…g（rn）为独立同分布的随机变量序列，根据辛钦大数定理，当n趋向无穷大时，对于任意的ε＞0，可得到公式（6）：

2.2 蒙特卡罗模拟的一般步骤

蒙特卡罗模拟的一般计算过程[6]主要分为以下几个步骤：

（1）建模：为待求解的问题构造一个合适的随机模型或概率模型f(r)，使所求问题的解恰好对应于该模型中随机变量的概率分布或统计特征；

（2）生成随机数：根据模型中的分布特征，使用计算机生成足够长的随机数序列；

（3）模拟求值：计算问题解的估计量，如函数值g(r)；

（4）统计：对模拟试验结果进行统计分析，如累加、求均值等；

（5）达到条件后退出：模拟次数和精度是否达到要求？

3 面向众核体系结构的实现

3.1 GPU和CUDA

众核GPU和多核CPU的执行能力具有很大差异，这是因为这两种处理器采用了完全不同的设计理念[7]。CPU由适合顺序串行处理的几个核心组成，而GPU则由数以千计的更小更高效的核心组成。如NVIDIA Tesla GPU由高度线程化的多核流处理器SM（Streaming Multiprocessor）阵列组成，每个SM又包含多个流处理器SP（Streaming Processor）。这种处理器体系结构非常适合运行大规模数据级并行任务。集成越来越多的处理器核心将成为处理器的发展趋势。

NVDIA推 出CUDA（ComputeUnifiedDevice Architecture）这一可扩展的并行编程模型，通过将海量线程自动调度到相应的处理器核上执行，大幅度提升计算性能[8]。在CUDA中，并行函数kernel在GPU上以SIMT（Single Instruction，Multiple Thread）的方式执行，即kernel中的每条指令被并行线程执行多次，但每次均处理不同的数据[9]。单个线程串行完成分配到该线程上的子任务，每个线程由单个处理器核完成，众多线程并行执行相同任务，达到真正意义上的数据级并行。

3.2 MC的并行程序设计

GPU通过单指令多数据（Single Instruction,Multiple Data，SIMD）指令类型来支持数据级并行。在这种结构中，GPU绘制多条流水线，控制部件向每条流水线分派指令，同样的指令被多个处理器核同时执行。

（1）OPS模型与流水线优化

OPS数据流并行编程模型，采用数据驱动的执行方式，是一种面向众核体系结构的流编程模型，该模型将流处理过程抽象成3类对象：计算处理单元Operator、管道Pipe和数据流Stream，如图2所示：

图2 OPS数据流并行编程模型

OPS模型采用有向图来描述处理过程。图2中的圆节点对应于Operator，表示计算；边对应于Pipe，表示数据依赖，边的方向表示数据流动的方向；流动的数据则对应于Stream。Stream是由一系列数据流组成，为Operator提供可并行处理的对象。

假设一个计算密集型应用按逻辑功能划分主要有A、B、C3个计算任务，根据OPS模型映射成SDF数据流图如图3所示：

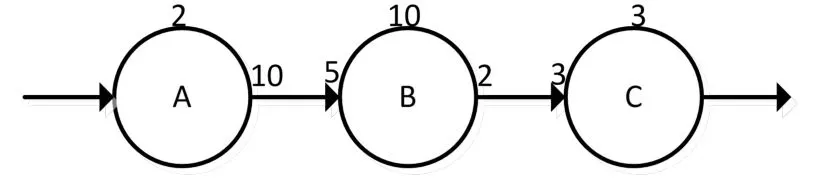
图3 简化的数据流图

图3中Pipe上的数字表示Operator的生产和消费能力。计算任务A每2个单位时间能产生10个单位的数据，B每10个单位时间消耗5个单位的数据并产生2个单位的数据，C每3个单位时间消耗3个单位的数据。显而易见，A、B和C之间的吞吐率没有得到很好地匹配。B成为整个流水线的瓶颈，所以流水线的性能受到极大的限制。

根据各个Operator的数据生产和消费能力，可以通过线性规划的方法确定各阶段计算任务的Operator的数量，然后调整Operator内在的循环迭代次数，最终实现Operator之间的吞吐率匹配，充分发挥流水线的并行性。假设X表示分配给某计算任务的Operator的个数，Y表示每次Operator循环迭代能产生的数据量，Z表示Operator每次循环迭代的数据消耗量，T表示每次循环迭代的耗时。当程序启动后，经过一段时间的初始化，流水线进入满负荷运转阶段，任意时间间隔内各计算任务间的数据产生量和消耗量是相等的，即可计算Operator的个数如公式（8）：

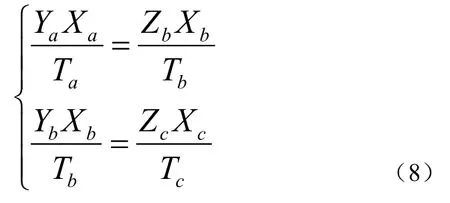
根据图3中的数据，若令Xa=1，求得Xb=10，Xc=2。

（2）MC模拟的多kernel任务执行过程

蒙特卡罗模拟过程按照逻辑功能大致可划分为生成随机数种子、并行随机数序列生成、并行模拟、归并等步骤。一个蒙特卡罗模拟任务的规模可以从模拟的次数N、一次模拟的宽度M、一次模拟的复杂度O这几个维度进行衡量，如图4所示：

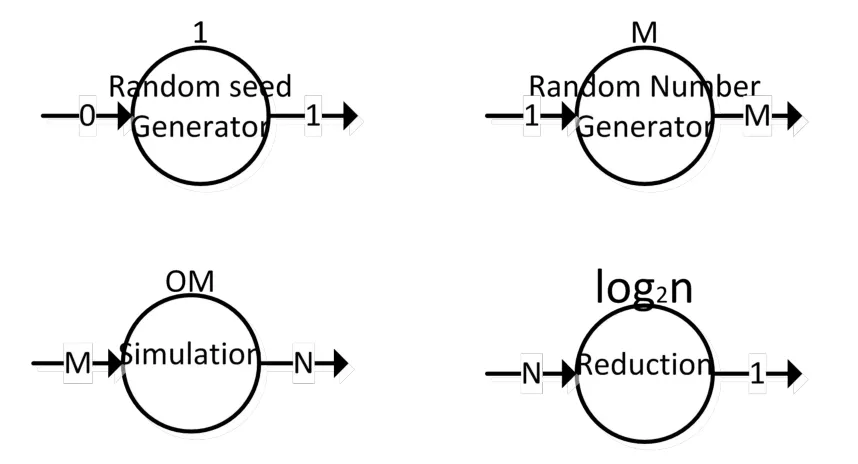
图4 蒙特卡罗模拟的任务分解

kernel内部均采用SIMD的数据级并行方式，从一定程度上提高了程序的运行效率，但是具有数据依赖关系的kernel之间本质上仍然是串行执行的，众核处理器的使用仅仅缩短了单个kernel的计算时间。为了达到更细粒度的数据级并行、以及MC模拟过程中多个功能步骤的任务级并行，大规模的蒙特卡罗模拟适合采用基于OPS数据流编程模型的流水线执行方式，如图5所示：

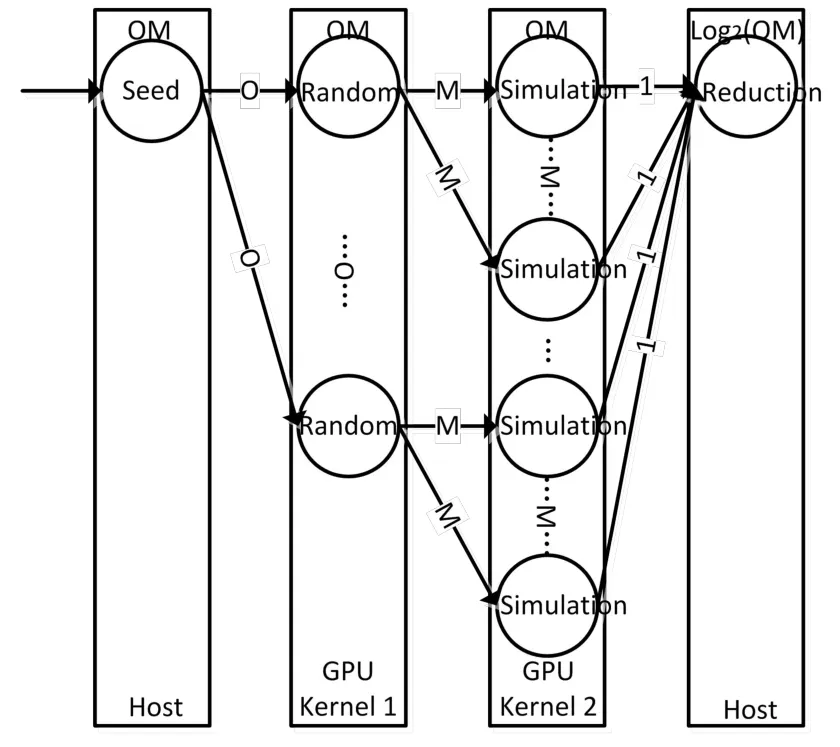
图5 MC基于OPS模型的流水线执行方式

如图5所示，Host端生成O个随机数种子；GPU端针对每个随机数种子启动一个线程，每个线程生成一个长度为M的随机数序列；针对每个随机数序列，在GPU端由M个线程进行模拟计算；模拟结果最终在Host进行统计归约。这种执行方式根据每个Operator的数据生产能力和消费能力，通过线性规划的方法，进一步确定每个功能步骤所需的Operator的个数，实现最小的程序执行时间及最大的数据吞吐率。该方式不仅适用于现代GPU众核处理器，同样也适用于更大规模的多GPU节点架构。GPU可以高效地进行并行计算，得益于其数以千计的处理器核心。SM中最多可同时驻留的线程数目是确定的，如果模拟的宽度M大于最大线程数，这必将影响蒙特卡罗模拟的运行时间[10]。对于这种更大规模的模拟场合，可以利用多个GPU节点的资源进行处理。通过高性能的互联网络可以将多个GPU节点连接起来，各个节点之间协调工作，提供一个单一的、完整的、集中的计算资源，供并行计算任务使用，从而获得较高的加速性能。实验二就证明了这种并行扩展能力。

4 实验

为了试验GPU的并行性能，我们进行了两次对比的模拟试验，实验一比较蒙特卡罗模拟过程在多核和众核两个计算平台上的执行时，GPU（2496个处理器核）相对于CPU的并行加速性能。实验二验证了GPU在多节点之间的并行扩展能力。

4.1 实验环境

试验用到的服务器为DELL PowerEdge R720型号，并配有两个Intel Xeon E5-2603四核CPU，16G内存和两个NVIDIA Tesla K20m GPU，每个GPU含有2496个处理器核。服务器上运行64位CentOS 6.4操作系统，CUDA Toolkit版本为5.5，用于开发的GCC版本为4.4.7。

4.2 实验一

在CPU平台上多次串行代码，并在GPU平台上多次运行并行代码，得到试验数据后处理并汇总于表2，第二列中单GPU执行时间和第三列中CPU执行时间都是多次运行后的结果的平均值。实验一中串行模拟和并行模拟的次数与所需时间的关系，如表2所示：

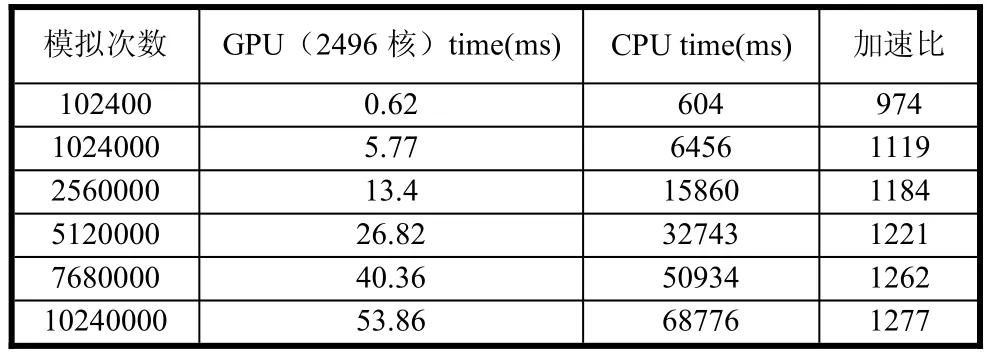
表2 模拟次数与加速比

从上表中的数据可以看出，随着模拟次数的增大，无论是串行模拟还是并行模拟，执行模拟过程所需的时间都在不断增加。相对于CPU串行过程，GPU众核处理器对蒙特卡罗模拟具有更快的执行速度。而且，随着模拟规模的增大，GPU相对CPU的加速比也有相应的增加，从这一点就可以说明GPU在处理大规模并行计算方面有着明显的优势。将单GPU处理相对于CPU的处理加速比以图的形式表达出来，加速比随模拟规模的增大有相应的增加，如图6所示：

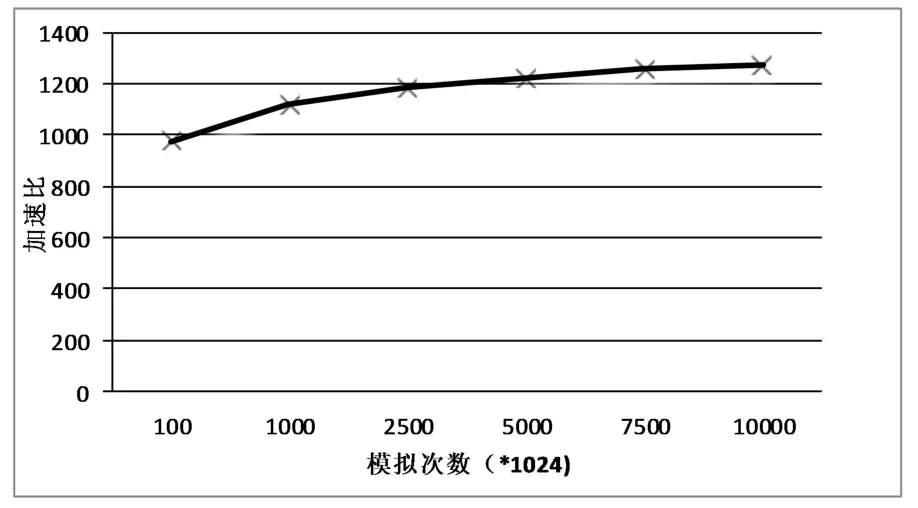
图6 随着模拟次数增加的加速比

4.3 实验二

实验二以单块GPU（2496核）模拟10240000次的执行时间为基准，计算出在其他处理器核数的况下执行10240000次模拟的加速比。加速比随处理器核数的变化如图7所示：

图7 随着处理器核数增加的加速比

在图7中，加速比并没有随着GPU节点数目的增加而成倍增加，而是一种近似线性的比例在逐渐增大。这是由于系统管理的开销、节点间通信开销和处理器核之间的同步开销等带来的副作用。

5 总结

建筑领域的成本估算是BIM技术的主要研究内容。用蒙特卡罗模拟成本估算是一个典型的计算密集型问题，通过对计算任务进行分解和重新设计，将模拟过程转化为多线程、数据并行的方式。随着GPU处理器核数的增大，庞大的数据量不再是影响大规模模拟性能的主要因素。集成越来越多的处理器核心是众核处理机架构的发展方向，这将为大规模数据量的应用提供一个良好的平台。

[1]张建平.建筑业应尽快推行建筑信息模型(BIM)技术.建筑技术[J].2011,42(1):9-13.

[2]孔嵩.建筑信息模型BIM研究.建筑电气[J].2013,4.

[3]Metropolis N,Ulam S.The Monte Carlo method[J]. Journal of the American statistical association,1949,44(247):335-341.

[4]朱鲲,柴跃廷,杨家本.经济系统风险模型及建模方法探讨[J].系统工程理论与实践.2003,11.

[5]肖刚,李天柁.系统可靠性分析中的蒙特卡罗方法[M].科学出版社,2003;

[6]Christian P.Robert, George Casella. Monte CarloStatistical Methods （ Second Edition ） [M]. Springer ,2004:134-146.

[7]David B.Kirk,Wen-mei W.Hwu.Programming Massivel y Parallel Processors[M].北京:清华大学出版社,2009.

[8]John Nickolls, Ian Buck, Michael Garland, KevinSkadron. Scalable Parallel Programming with CUDA[J].GPU Computing Queue Homepage archive Volume 6Issue 2, 2008.

[9]Nvidia.CUDA Programming Guide Version 4.0[OL]: http://www.nvidia.com/object/cuda_home.html,2012;

[10]Alerstam E,Svensson T,Andersson-Engels S,et al. Parallel Computing with Graphics Processing Units for High-speed Monte Carlo Simulation of Photon Migration [J].Journal of Biomedical Optics Letters,2008,13(6): 060504.

Research on Cost Estimation Based on Monte Carlo in BIM

Zhao Qianchun,Hu Weisong,Wu Baifeng
(School of Computer Science,Fudan University,Shanghai 201203,China)

In Recent years,Building Information Model(BIM)has been the key technology of architecture industry,which represents the developing direction of architectural design technology.Cost estimation is one of the important parts of BIM technology.Generally speaking,it is difficult for the common methods to get the exact cost value which is affected by many risk factors.Monte Carlo simulation method is a strong tool for researching the complex process with many influence factors,but the massive data amount has limited its application.Based on the architecture of many-core processors,Monte Carlo process can be designed as a large-scale data-level parallel computing,which makes the massive data amount resolved by increasing processor cores.The experiment results have proved the ideal parallelism and scalability of the process.

BIM;Cost Estimation;Monte Carlo;Data-Level Parallelism;Scalability

TP319

A

1007-757X(2015)06-0001-05

2015.03.09）

鲁班软件大学合作计划项目

赵倩纯（1989-），女，复旦大学，计算机科学技术学院，硕士研究生，研究方向：高性能计算，上海，201203

胡伟松（1989-），男，复旦大学，计算机科学技术学院，硕士研究生，研究方向：高性能计算，上海，201203

吴百锋（1963-），男，复旦大学，计算机科学技术学院，教授，硕士，研究方向：高性能计算，嵌入式系统，上海，201203