无限区间上p-Laplacian方程解的存在性
武 晨
(江苏联合职业技术学院南京分院,江苏南京 210019)
无限区间上p-Laplacian方程解的存在性
武 晨
(江苏联合职业技术学院南京分院,江苏南京 210019)
本文研究无限区间上非线性p-Laplacian方程解的存在性,通过利用Leray-Schauder连续度方法得到解的存在性结果。
Caratheodory函数;p-Laplacian算子;边值问题
1 提出问题
在本文中,我们研究非线性一维p-Laplacian方程
其中,φp(s)=|s|p-2s,p>2.
f:[0,+∞)×R2→R关于L1[0,+∞)是个Caratheodory函数,p(t)∈C[0,+∞)∩C1(0,+∞),且对于所有的t≥0恒有p(t)>0成立,α≥0,β≥0,且不同时为0.

为了方便起见,定义如下记号:
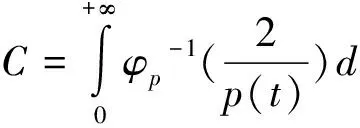
2 一些定理和引理
定理2.1 设X是一个Banach空间,T:X→X是全连续算子,如果存在R>0,对于λ∈(0,1),满足u=λTu,,都有‖u‖≤R成立,则T有一个不动点.
定理2.2[1]设X是[0,+∞)上所有连续有界泛函组成的空间,且S⊂X,则S在X中是列紧的当且仅当下面的条件成立:①S是X中的有界集;②S中的所有泛函在[0,+∞)的任意有限子集内都是等度连续的;③S中的所有泛函都是等度收敛的.

引理2.1 如果g∈L1[0,+∞),则方程p(t)φp(u′(t))′=g(t)对应于边值问题(2),且满足α>0有唯一解:

(3)
引理2.2 如果g∈L1[0,+∞),则方程p(t)φp(u′(t))′=g(t)对应于边值问题(2),且满足α=0有唯一解:

(4)
引理2.3 如果g∈L1[0,+∞),则(3)中的u(t)满足:‖u‖∞≤Aφp-1(‖g‖)1,‖u′‖∞≤Bφp-1(‖g‖)1.
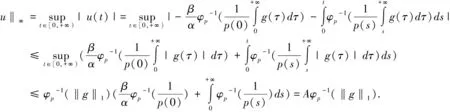


引理2.4 如果g∈L1[0,+∞),则(4)中的u(t)满足:‖u‖∞≤|u(0)|+Cφp-1(‖g‖)1,‖u′‖∞≤Bφp-1(‖g‖)1.
定义算子:

(5)

(6)
引理2.5 算子T1,T2:X→X是全连续算子.
证明 为了证明T1是紧算子,只需要证明T1把X中的任何有界集映成相对紧集.设K⊂X有界,则必存在r>0,使得r=sup{‖u‖:u∈K}.由于f:[0,+∞)×R2→R关于L1[0,+∞)是个Caratheodory函数,从而存在L1可积的函数αr,使得对所有的u∈K和几乎处处的t∈[0,+∞)都有|f(t,u(t),u′(t))|≤αr(t)成立.
从而对任意的u∈K,有

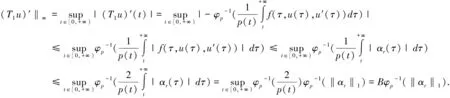
从而,‖T1u‖≤max{A,B}φp-1(‖αr‖1),即T1(K)在X中有界.
对任意L1,L2∈[0,+∞),ε>0,存在δ>0,使得对任何子区间[t1,t2]⊂[L1,L2],满足|t2-t1|<δ,都有
|T1u(t2)-T1u(t1)|=



因此,T1(K)在[0,+∞)上的任意有限子集内是等度连续的.



所以T1(K)是等度收敛的,这样就满足定理2.2的所有条件.从而根据定理2.2可知,T1(K)是列紧的.由Lebesgue控制收敛定理可得,T1是连续的,所以T1:X→X是全连续算子.同理可得T2:X→X也是全连续算子.
3 主要结论
定理3.1 假设是函数f:[0,+∞)×R2→R是L1-Caratheodory函数,如果存在函数α,β,γ:[0,+∞)→[0,+∞),α,β,γ∈L1[0,+∞),使得|f(t,z1,z2)|≤α(t)|z1|+β(t)|z2|+γ(t),a.ein[0,+∞);A‖α‖1+B‖β‖1<1成立,其中A,B由本文第一节给出,则当α>0时,边值问题(1)(2)对任何γ∈L1[0,+∞)至少有一个解.
证明 考虑对于λ∈(0,1),方程
(p(t)φp(u′(t)))′=λf(t,u(t),u′(t)).a.e.in(0,+∞).
(7)
满足边值条件(2),接下来证明所有满足边值问题(2)(7)可能的解都有一个不依赖于λ∈(0,1)的先验估计.根据引理2.3和(7),有
‖(p(t)φp(u′(t)))′‖1=λ‖f(t,u(t),u′(t))‖1≤‖α‖1‖u‖∞+‖β‖1‖u′‖∞+‖γ‖1
≤A‖α‖1φp-1(‖p(t)(φpu′))′‖1)+B‖β‖1φp-1(‖p(t)(φpu′))′‖1)+‖γ‖1




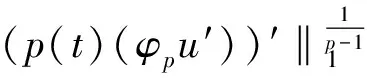



满足边值问题(2)(7)的解在L1[0,+∞)中都有一个不依赖于λ∈(0,1)的先验估计,由引理2.3和以上不等式可知

易知边值问题(1)(2)有解当且仅当算子T1有不动点.T1是全连续的,由上述不等式可知定理2.1的条件成立,可知T1有一个不动点,即是边值问题(1)(2)的解.
类似地,我们可以得到如下定理.
定理3.2 假设f:[0,+∞)×R2→R是L1-Casratheodory函数,如果存在函数α,β,γ:[0,+∞)→[0,+∞),α,β,γ∈L1[0,+∞),使得|f(t,z1,z2)|≤α(t)|z1|+β(t)|z2|+γ(t),a.ein[0,+∞);C‖α‖1+B‖β‖1<1成立,其中B,C由本文第一节给出,则当α=0时,边值问题(1)(2)对任何γ∈L1[0,+∞)至少有一个解.
[1]R.P.Agarwal,D.O.Regan.InfiniteProblemsforDifferential,DifferenceandIntergalEquations[C].KluwerAcademic,2001.
[2]LiuBaofang,ZhangJihui.Theexistenceofpositivesolutionsforsomenonlinearboundaryvalueproblemswithlinearmixedboundaryconditions[J].J.Math.Anal.Appl,2005(309):505-516.
[3]KosmatovN.Secondorderboundaryvalueproblemsonanunboundeddomain[J].NonlinearAnal,2008(68):875-882.
[4]KongLingju.Secondordersingularboundaryvalueproblemswithintegralboundaryconditions[J].NonlinearAnalysis,2010(72):2628-2638.
[5]JiYude,GuoYanping.Theexistenceofcountablymanypositivesolutionsforsomenonlinearnthorderm-pointboundaryvalueproblems[J].J.Comut.Appl.Math,2009(232):187-200.
[6]LiangSihua,ZhangJihui.Theexistenceofcountablemanypositivesolutionsfornonlinearsingularm-pointboundaryvalueproblemsonthehalf-line[J].J.Comput.Appl.Math,2008(222):229-243.
The Existence of Solution forp-LaplacianEquation on an Unbounded Domain
WU Chen
(Branch of Nanjing Jiangsu Union Technical Institute, Nanjing Jiangsu 210019, China)
In this paper, we consider the existence of solution forp-Laplacianboundary value problem on an unbounded domain.By usingLeray-SchauderContinuation Principle, we obtain the existence solution for this boundary value problem.
Caratheodoryfunction;p-Laplacianoperator; boundary value problem
2015-07-12
武 晨(1985- ),男,安徽宿州人,江苏联合职业技术学院南京分院讲师,硕士,从事微分方程研究。
O
A
2095-7602(2015)10-0001-04

