激光信号雨滴衰减特性研究

韦道知， 肖 军， 张东洋， 王 柯

（空军工程大学防空反导学院，陕西 西安710051）

0 引言

激光引信具有波束窄、方向性好、能量集中等特点，具备良好的抗电磁干扰能力，在航空炸弹、火箭、飞航导弹及反坦克导弹上得到了广泛应用。

降雨对激光产生严重的衰减，给激光探测带来一定影响。本文基于夫琅禾费衍射和几何光学散射理论，建立雨滴对532nm 和1 064nm 激光光束的传输衰减模型，以Gamma分布作为雨滴谱分析计算两种波长激光在不同降雨量下的衰减特性，并通过仿真验证了雨滴衰减模型。

1 激光信号降雨衰减特性

激光探测系统在大气中的传输特性为［1］

式中：PR为探测器接收的激光功率；PT为激光器发射功率；τE为发射光学系统的透射率；τR为接收光学系统的透射率；τF为窄带滤光片的透射率；AR为接收机光学系统孔径面积；ρ为目标物的反射率；β为目标反射表面法线与光轴之间的夹角；r为激光束传播距离；α（r）为距离r处的大气衰减系数。

为了评价激光探测系统的传输性能，需考虑复杂大气环境的影响。降雨影响激光能量传输，会导致严重衰减。雨滴对激光能量的衰减包含吸收和散射两部分，波长为λ 的激光束在降雨中的衰减系数可表示为

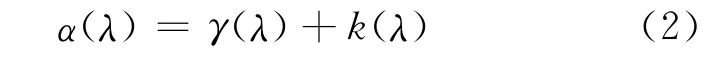
式中：γ（λ）为散射系数；k（λ）为吸收系数。散射系数的计算式为

式中：σs（D）为雨滴微分散射截面；N（D）为雨滴尺寸分布函数。

1.1 雨滴尺寸分布函数

雨滴尺寸分布是指在单位空间体积内，直径在D ～D+Δd的雨滴数目，即单位体积内雨滴大小的分布。雨滴尺寸分布常用M-P分布、对数正态分布和Gamma分布函数来描述。

M-P分布是Marshall和Palmer于1948 年提出的，其形式为

研究发现M-P谱中的参数N0还与降水强度P 有关，不是一个固定的常数。

Gamma分布是在M-P分布中引入一个形状因子μ：

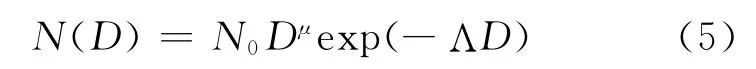
我国从20世纪60年代开始就对雨滴谱进行了观测和研究，对不同地区的降水类型的雨滴谱分布形式做了拟合。研究表明，M-P 分布对于稳定降水的雨滴谱拟合效果较好，对于起伏变化较大的降水，在小滴和大滴段拟合误差较大。相比于M-P分布，Gamma分布对各类雨滴谱的拟合效果都很好，尤其对于小滴段的描述。

根据1992年夏季广州地区雨滴尺寸分布测量数据和广义Gamma分布模型［2］，通过优化计算得到广州地区雨滴尺寸分布的模型：

这一模型与当地实测的雨滴分布有较好的一致性。

1.2 雨滴散射衰减系数

激光光束在降雨介质中传播时，会发生雨滴的吸收和散射。散射是指光线通过不均匀的介质而偏离其原来的传播方向，散开到所有方向的现象［3］，导致原来传播方向上的激光光束能量的衰减。激光束在雨中传播时，往往将雨滴视为球形粒子，可以用米氏散射理论来严格描述球形粒子的光散射过程。米氏理论虽然精确，但计算量大，特别是随着颗粒粒径的增加，求解的复杂叠加项就越多，带来的计算误差就越大，因此米氏理论的数值计算受到粒子尺寸参数的限制，对于雨滴等大粒子的散射计算就不再使用了。

考虑到雨滴直径远大于激光波长，雨滴对激光的散射也就是微粒的尺寸参数α＞1时的散射问题。研究表明，当颗粒的尺寸远大于激光波长λ时，光散射主要集中在前向角度范围内，因此可以用夫琅禾弗衍射理论计算颗粒前向散射［4］。由于衍射光的分布范围窄，84%的衍射光能都集中在θd＝arcsin（1.22π／α）的艾里斑内，在小散射角度范围内，夫琅禾弗衍射可近似代替光散射计算。对于大角度的光散射分布，还需考虑光束在颗粒表面产生的反射和折射的影响，也称之为光束几何散射。

根据巴比涅互补原理，除去中心点外平面不透光圆屏的衍射光强分布与相同大小的圆孔衍射光强分布完全相同。因此在一定区域内，可由圆孔的夫琅禾弗衍射得到圆球颗粒的夫琅禾弗衍射光强。

直径为D 的雨滴在距离r 处的衍射光强为［5］

对式（6）进行积分推导，可得雨滴的夫琅禾弗衍射衰减截面为

式中：I0为入射光强度；尺寸参数α＝πD／λ；θ为衍射光与入射光方向的夹角；J0与J1分别为零阶、一阶贝塞尔函数。

图1为球形颗粒的光束几何散射的示意图，平行光从某一角度入射后，经过球形颗粒的光被部分反射和折射。

图1 光的几何散射

Van DeHulst给出了球形颗粒在平面光入射下经过某一次折返或反射后的两个不同偏振方向的初射光强度分布表达式为

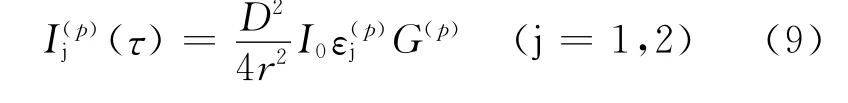
式中：p为第p 条初射光线；τ为入射角余角；I0为入射光强度；D 为颗粒直径；r为颗粒到观察面的距离；εj和G 分别为

式中：r1和r2为菲涅耳反射系数。

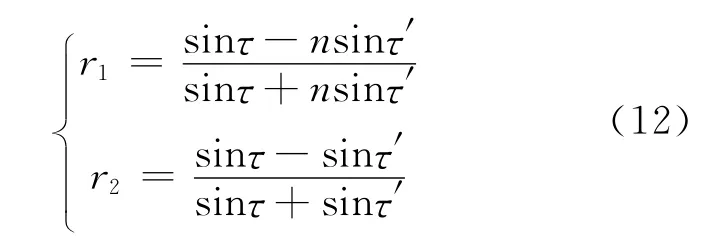
式中：n为水的负折射率实部。

引入无量纲强度函数i（p）j（α，τ）＝α2ε（p）jG（p），它是基于角度τ的一次反射或折射强函数。对于给定散射角度θ下各次折、反射的总强度函数为

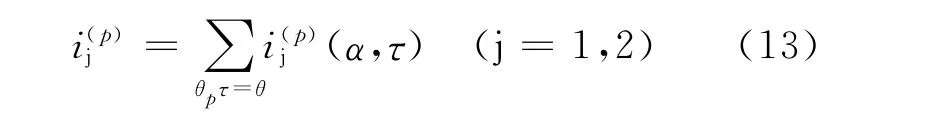
数值计算表明，对于非吸收颗粒，96%以上的几何散射光能由反射和第一次折射产生，而对于吸收颗粒比例更高，且第一次反射的0号线光强度远比透明颗粒情况下的1号光线弱。对于半径小于3mm 的水滴，其反射能量与总能量的比值小于1%［6］。因此，可以将吸收性质颗粒内部经过2次以上反射后的出射光能忽略，而只考虑第一次折射光强。总强度函数可以近似由第一次折射光强度函数表示：

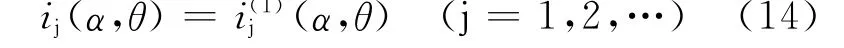
将以上各式联立，对于偏振角为φ 的线偏振激光，粒子散射光强角度分布为

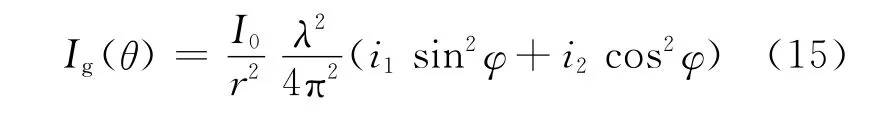
单个球形雨滴的几何散射衰减截面为

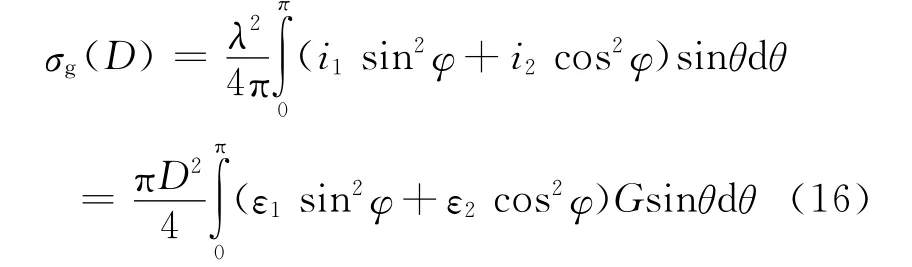
球形雨滴对激光光束的散射衰减截面模型为

由上述分析可知，雨滴的激光散射由夫琅禾弗衍射和几何散射构成。对直径为0.5 mm 和1mm的球形雨滴，计算得到角散射截面分布σs（D，θ）如图2、图3所示。

从图中的数据可以看出，更多的散射光集中到前向较窄的衍射瓣中，在较小的角度范围内，衍射光主要为透射光，当散射角度增大时，几何散射光占主要地位，且随着粒子直径的增大，角散射截面增大。

1.3 降雨衰减的数值计算及分析

图2 雨滴角散射截面（D＝0.5mm）

图3 雨滴角散射截面（D＝1mm）

激光的传输衰减特性与激光波长和气候条件有关。如前所述，激光光束在降雨条件下传播时的衰减率，由吸收和散射两部分组成。吸收随着波长而发生变化，散射影响光束能量的空间分布，使原来传播方向上的激光光束能量发生衰减。

下面分别对532nm 的绿激光和近红外波段的1 064nm 激光进行降雨衰减的分析计算。

水的吸收作用与该波长下水的复折射率虚部有关，当负折射率很小时吸收作用不显著。已知液态水在532 nm 波长下的复折射率虚部为1.32×10-9，水对绿激光光束的吸收近似为零，因此雨滴对532nm 波长的激光只存在散射作用，总衰减只由散射决定。1 064nm 激光下水的复折射率虚部相对较大，存在相应的吸收率，因此雨滴对1 064nm 激光的衰减需要同时考虑散射与吸收。根据计算，得到不同波长激光在不同降雨状况下的散射系数和吸收系数，如表1与表2所示。

由表1和表2可知，波长为532nm 的激光与波长为1 064nm 的激光散射系数几乎相当，但会随着波长的增加有微小增加。随着降雨量的增加，波长为1 064nm 激光的降雨衰减中，吸收损耗高于散射损耗，雨滴对激光束的吸收作用明显，吸收系数也随着降雨强度的增大而增大。

表1 532nm 激光散射吸收系数

表2 1 064nm 激光散射吸收系数

2 仿真验证

传 输 距 离 为100 m 时，波 长 为532nm 和1 064nm的激光光束的透射率随降雨量的变化曲线分别如图4、图5所示。由图可知，两波长的激光透射率都随着降雨量和传输距离的增大而降低。532nm 的激光因为只存在散射衰减，在暴雨中仍有较高的透射率。1 064nm 的激光由于同时存在吸收损耗和散射衰减，暴雨中的透射率近似为零。

图4 激光在不同降雨量时的透射率（传输距离100m）

图5 激光在不同降雨量时的透射率（传输距离200m）

3 结论

对两种波长激光在降雨环境中的透射率进行了模拟计算。计算结果表明：不同波长的激光的吸收损耗差异很大，这与某一波长下水的负折射率虚部有关，虚部越小吸收作用越不明显；对于散射衰减，二者的差异并不大。所以决定激光在降雨环境下衰减的决定性因素是吸收衰减。

［1］ 邓方林，张翼飞，杨辉.弹道导弹激光引信测距性能研究［J］.系统仿真学报，2005，17（6）：1476-1479.

［2］ 赵振维.广州地区雨滴尺寸分布模型及雨衰减预报［J］.电波科学学报，1995，10（4）：33-37.

［3］ 邵理堂，王式民，汤光华，等.颗粒物Mie散射对差分吸收光谱技术的影响［J］.光学学报，2009，29（3）：594-601.

［4］ W.J.Wiscombe.Improved Mie Scattering Algorithms［J］.Applied Optics，1980，19（9）：1505-1509.

［5］ 徐啟阳，杨坤涛，王新兵，等.蓝绿激光雷达海洋探测［M］.北京：国防工业出版社，2007.

［6］ Rass O N，Bradley S G.Model for Optical Forward Scattering by Nonspherical Raindrops［J］.Applied Optics，2002，41（24）：5130-5141.