用于小行星探测的多光谱图像处理技术
黄 勇, 程晓瞳, 雷 威
(上海无线电设备研究所,上海200090)
0 引言
小行星探测具有重大的科学意义和现实意义,已有多个国家及航天局发射多个搭载各种探测载荷的航天器,对多个小新星进行了较全面的探测[1-2]。如2007年由美国航天局(NASA)发射的探测“灶神星”和“谷神星”的“黎明号”探测器,2004年由欧空局(ESA)发射的探测彗星的“罗塞塔号”探测器,2003年由日本航天局发射的“隼鸟号”探测器等[3],它们均携带了高清CCD 相机和红外光谱仪(或红外探测仪),其探测任务都包括小行星表面高清成像和物质分析两方面。
多光谱成像仪工作在可见光/近红外波段时,不仅可对观测区域成像,且可通过获取所观测物质的光谱反射信息,进行物质的分析与鉴定,适用于小行星这种不适合着陆探测且几乎没有大气覆盖的探测环境。多光谱成像仪所带来的大信息量是以大数据量为代价的,这给远距离数据回传带来了较大压力,也是应用多光谱成像仪进行深空探测的主要瓶颈。这里提出了一个集降维、压缩和去噪为一体的多光谱图像处理技术,可实现图像的高倍且最优化的有损压缩,大幅度降低图像数据总量。传输压缩后的图像数据可大幅减少数传压力。
1 多光谱成像仪
1.1 成像原理
多光谱成像是一种被动光学探测方式,其原理是不同物质对光的反射谱线不同,同一物质对不同波长光的反射强度也不同。通过分光器件可以在不同波长的光波段内分别成像,成像结果按波长依次排列得到多光谱图像。基于此图像可实现成像和光谱分析两部分功能。图1中,雪地、小麦、沙漠和湿地四种地物的光谱曲线在可见光到近红外(0.4μm~1.2μm)范围内有明显的差异,利用这些差异特征可以对光谱曲线作相似度判定,从而区别或鉴定物质成分。
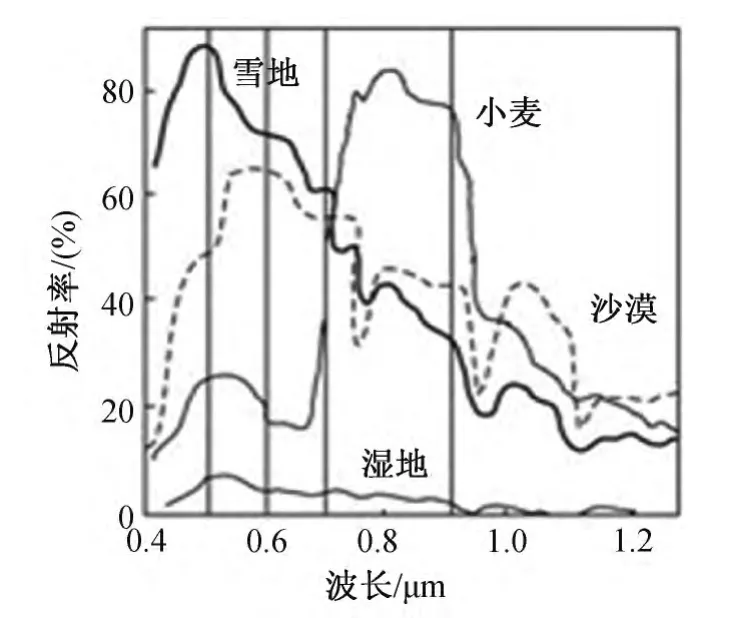
图1 不同物质的光谱曲线示意图
多光谱成像仪的成像结果是同一地物在不同光波段的三维图像,包括一个光谱维度和两个空间维度。按照光谱维度划分的精细程度,即光谱分辨率的高低或一定波长范围内的波段数多少,可以将光谱图像分为多光谱、高光谱和超高光谱图像[4]。高光谱图像的波段数多达上百个,超高光谱图像甚至包含上千个波段,这些图像中包含了丰富而精细的光谱特征,可在微小差别的基础上实现近似物的精确区分和鉴定,但二者的数据量过于庞大,不适合星上即时处理和远距离数据回传。多光谱图像有几个到几十个波段,数据量适中且处理压力较小。目前技术条件下,选用多光谱成像仪在满足探测需求的同时,可以节省计算资源和存储成本。
1.2 系统组成
多光谱成像仪是照相机和光谱仪结合的产物,它主要由光学部分和电子学部件构成。其中,光学部分完成聚光、准直和分光等功能,电子学部件主要完成成像、存储及处理等功能。图2中,入射狭缝实现空域滤波,保证只有一束平行光可以投射到分光光路上。分光棱镜、傅里叶透镜和棱面镜共同构成分光光路,将狭缝透射的平行光按频率(波长)折射分光,这种“空间调制型干涉分光”的分光方式相比传统的“棱镜分光”或“迈克尔逊干涉分光”,在光通量、弱光下成像信噪比等方面具有更好的性能[5]。阵列CCD 完成光电转换以得到一维空间加一维光谱的二维图像。
利用狭缝和分光得到一维空间和一维光谱后,通过探测器的飞行方向推扫即可得到另一维空间数据,如此得到完整的多光谱三维图像。为获取高空间分辨率的观测区域图像,可保持CCD阵元数不变而将入射光路的视场角做窄,单个阵元所承载的空间面积降低,空间分辨率得到提高,阵元数不变则数据总量不会增大,但是推扫观测的区域宽度会减小。
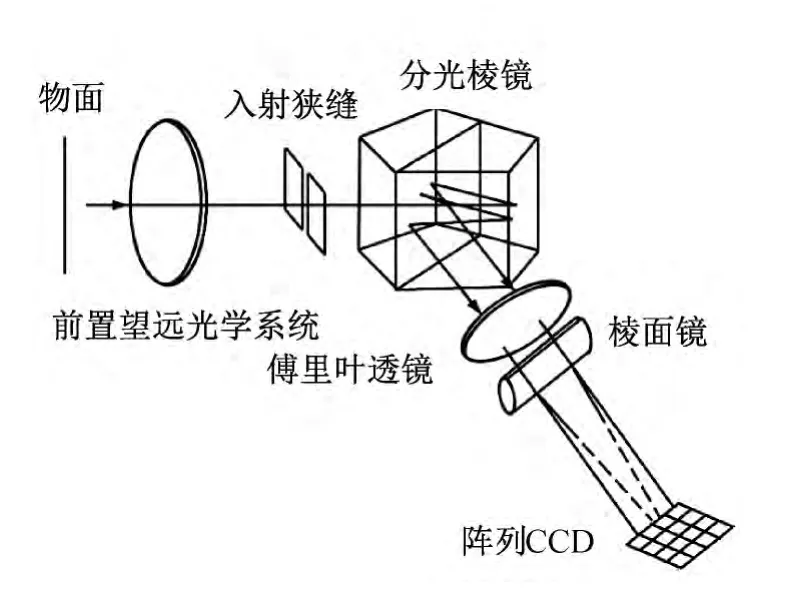
图2 多光谱成像仪光学部分示意图
2 多光谱处理技术
2.1 图像特性分析
多光谱图像是对同一地物在不同波段上的成像,其相邻波段图像之间具有很强的相关性。这种相关性的强弱是由两个波段的波长近似程度决定的,波长越相近则相关性越强,因此多光谱图像的光谱分辨率越高,相邻波段之间的相关性越强。经过三维的离散余弦变换(DCT),三维的离散小波变换(DWT)或Tucker分解等去相关变换后,图像能量在变换域向前高度集中,如图3所示,数据源为64个波段多光谱图像。
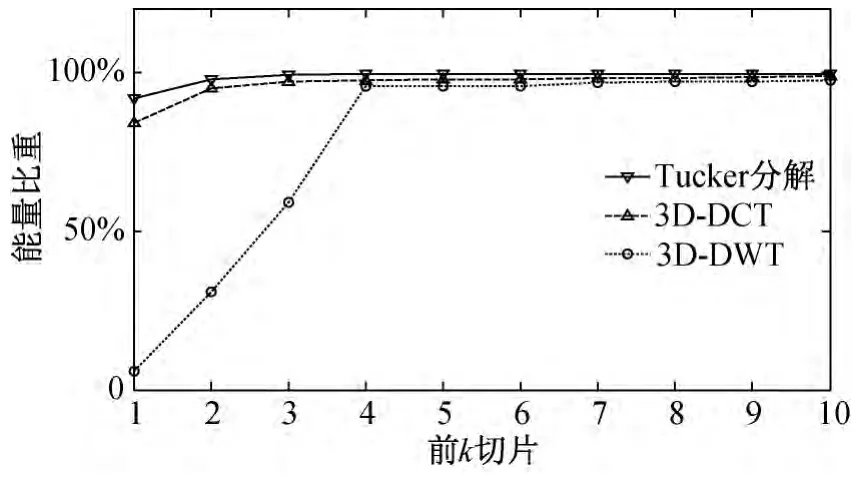
图3 变换域中光谱维度能量集中分布曲线
变换域中,统计光谱方向每个波段的二维图像能量得到能量切片k,则变换后的多光谱能量几乎全部集中于前10个切片中,其余54个切片几乎不包含能量但占了很大部分数据量,这些尾部切片多为不必要的噪声成分和高频分量。这表明,多光谱图像有很大的数据冗余,去除这些冗余可大幅度压缩图像数据量[6]。图3 还表明,Tucker分解的去相关能力比DCT 和DWT 都要强,适合于压缩前对图像去相关。
2.2 Tucker分解原理
Tucker分解被称为高阶主成分分析(PCA),继承了PCA 变换的最优去相关能力,因此它的去相关能力强于DCT 和DWT。Tucker分解可以对任意维数的数据,或称之为张量,根据指定维度进行正交分解,分解得到核张量(Core Tensor)的能量是集中分布的,其计算公式[7-8]为
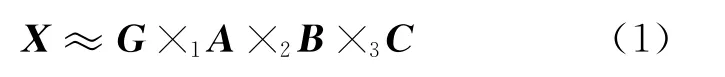
或
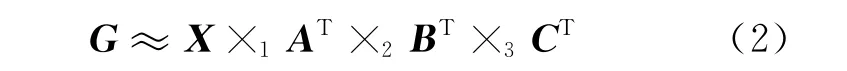
式中:X 是待分解张量;G 是分解得到的核张量;A,B,C是正交矩阵;×n表示第n维度的张量向量积;T 表示矩阵转置。分解示意图如图4所示。
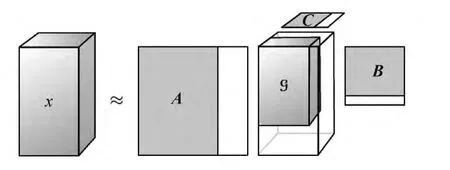
图4 Tucker分解示意图
利用Tucker分解可对原始多光谱图像很好地去除相关性,便于后续分离冗余成分。
2.3 压缩效果评价准则
以压缩比和信噪比作为评价准则。压缩比定义为
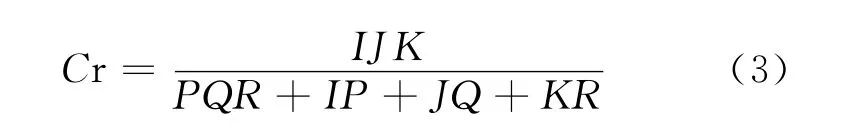
式中:I,J,K 表示原始图像数据维度;P,Q,R 表示核张量数据维度。
信噪比定义为
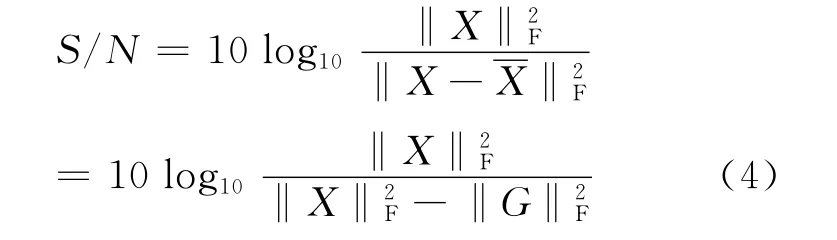
式中:‖·‖2F为张量的Frobenius范数的平方,用于计算图像能量;X 为原始图像张量;为重建图像张量。式(4)可由文献[7]中给出的两个引理推导,其含义是以原始能量对误差能量倍数定义重建信噪比,评价压缩过程中的能量损失。压缩多光谱图像的目标就是一定压缩比下使重建信噪比最高,也就是核张量能量‖G‖2F最大。
2.4 算法设计
基于Tucker分解的多光谱图像压缩处理技术是对完整去相关后的核张量和投影矩阵按最优维度自适应截断,本质是一个数据降维过程。降维后的数据是根据压缩比分离出噪声成分和不必要高频分量后的结果。数据量大幅减少的同时图像几乎无能量损失,整体上又是图像压缩过程,因此这种处理技术是集降维、压缩和去噪为一体的多光谱图像预处理方法。算法流程如图5所示。
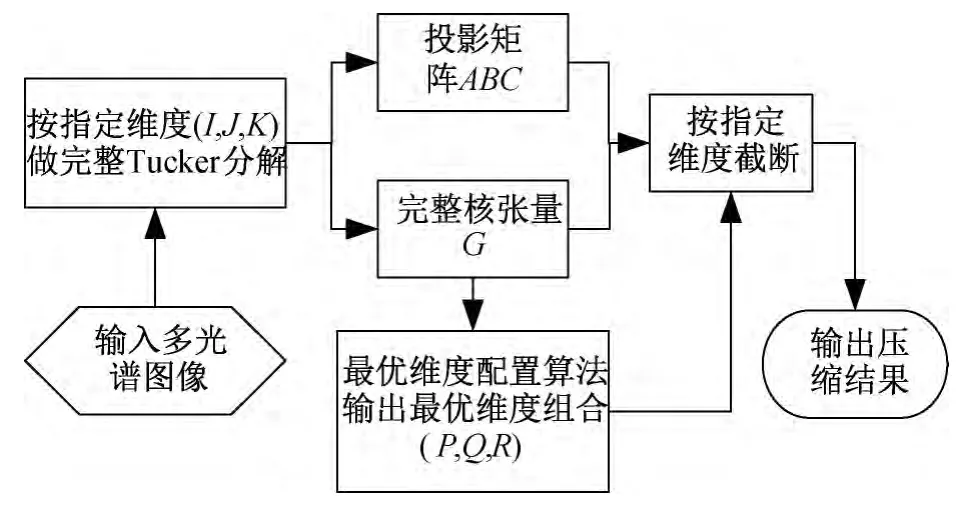
图5 基于Tucker分解的算法流程
确定的多光谱图像数据的完整Tucker分解结果是确定的,影响压缩比和信噪比的唯一因素是为充分保留能量而选取的核张量三维(P,Q,R),这种核张量三维的确定过程成为最优维度配置问题,是本文提出算法的核心问题。
2.5 最优维度配置算法
最优维度配置算法的根本目标是找寻一定压缩比下使重建信噪比最高的核张量三维(P,Q,R),这是个利用一个半条件求解三个未知数的奇异方程问题,其结果是不唯一的,要从通解中确定最优解需要补充潜在条件并逐步优化搜索。鉴于多光谱图像的空间维度两个方向,即行与列的相关性近似,可一般性假设行列方向具有相同的压缩潜力,则有:P/I =Q/J。此外,多光谱图像的光谱相关性远强于空间相关性,可优先自光谱维展开搜索,确定使‖G‖2F最大的(P,Q,R)。
算法的仿真结果如图6所示。
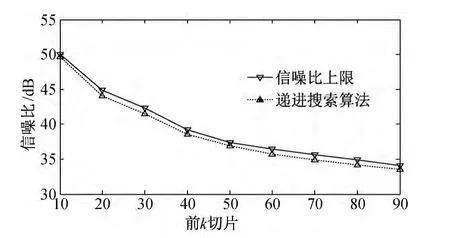
图6 递进搜索算法压缩效果
仿真数据源是256×256×64 的Cuprite地区多光谱图像。由图6可见,递进搜索算法可以搜索到近似解而不是真正的最优解,这是由于基于假设的搜索算法有一定误差,多光谱图像的行列相关性不会严格相同,这导致搜索算法不够精细,会在最优解附近振荡而无法收敛于最优解。
为解决上述问题,可采用常用的优化算法对递进搜索结果进一步优化,如遗传算法、蜂群算法和粒子群算法等。因为粒子群优化算法(Particle Swarm Optimization,PSO)搜索速度快且原理简单[9],本文采用它做后期优化搜索。优化算法的全局搜索能力和搜索精度是一对不可调和的矛盾,搜索精度高必然全局搜索能力弱,因此搜索初值的选定至关重要。初值合适则有利于搜索避开局部解而收敛于全局解。递进搜索结果恰好提供全局解附近的近似解作为初值,使PSO 算法快速搜索到最优解。改进后的算法仿真结果,如图7所示。
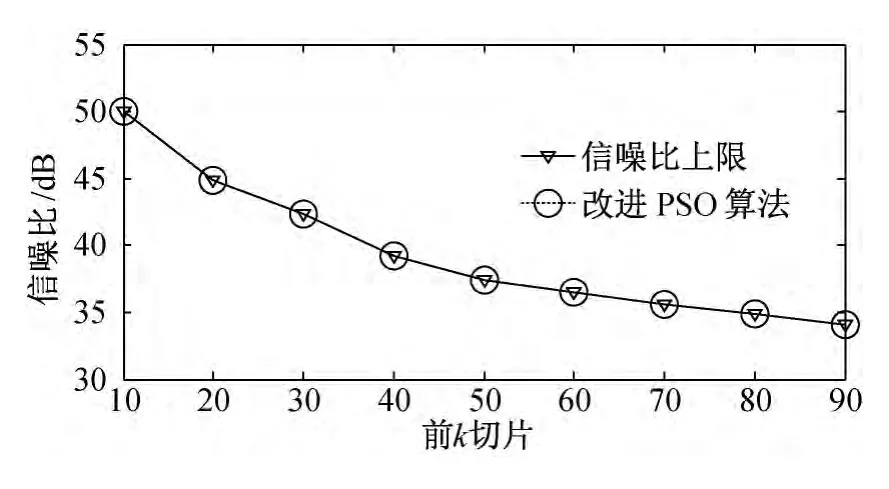
图7 递进搜索加粒子群优化压缩效果
由递进搜索算法提供初值还可提高粒子群算法搜索速度,仿真结果如图8 所示,改进的PSO算法比单纯PSO 算法搜索速度更快。
3 算法对比仿真
为验证本文提出算法的优越性,利用基于对称DWT 和非对称DWT 的3D-SPIHT 算法作为对比对象[10],在压缩效果和速度上的仿真结果如图9和图10所示。
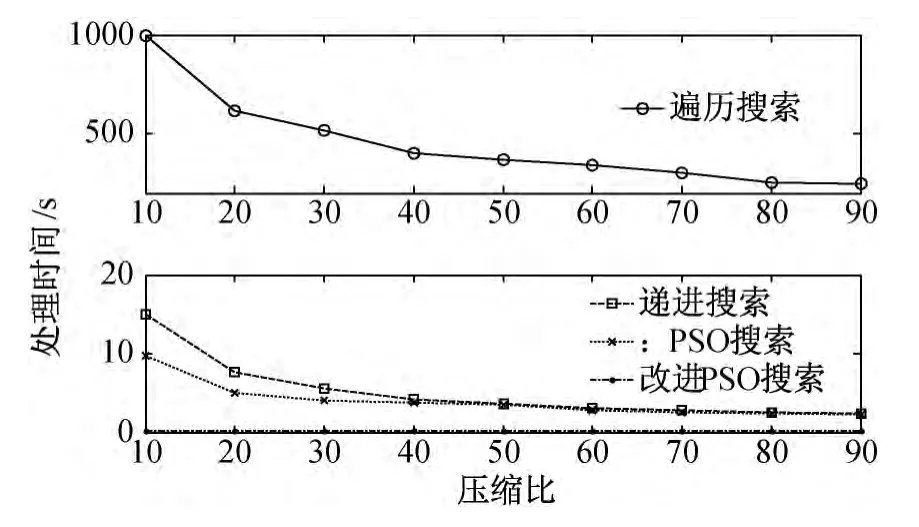
图8 搜索时间对比曲线
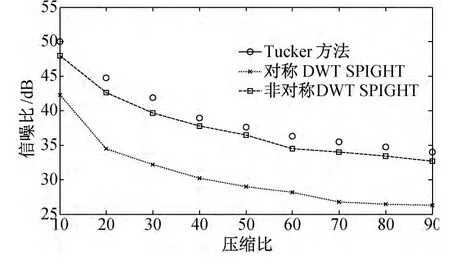
图9 压缩效果对比曲线
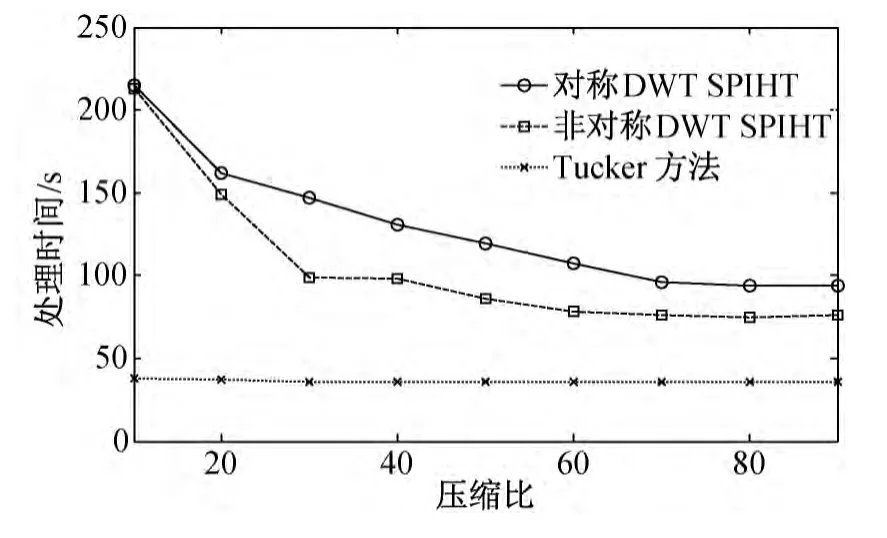
图10 压缩速度对比曲线
由图9可见,本文提出的方法(即张量方法)在相同的压缩比下可得到更高的重建信噪比,这是由于Tucker分解具有比DWT 更强的去冗余能力。由图10可见,本文提出的方法在相同的压缩比下具有远快于其余两种方法的处理速度。这是由于本方法更注重图像的变换域分析,将计算资源集中于Tucker分解,而舍弃了最复杂最耗时的编码过程。
4 结论
文章介绍了多光谱成像仪工作原理及其系统组成,分析了其在小行星探测中的可行性。研究了多光谱图像特性后,为解决大数据量的远距离传输问题,最终提出了基于Tucker分解的,集降维、压缩和去噪一体的图像处理技术。多光谱成像仪作为独立载荷,可同时完成照相机和光谱仪的行星表面成像和物质分析功能,适用于小行星这种小质量且几乎无大气衰减的探测环境。本文提出的预处理算法能够以较高的图像重建质量实现多光谱图像的快速有损压缩,相比同类算法在压缩效果和速度上都有较大优势。
[1] 徐伟彪,赵海斌.小行星深空探测的科学意义和展望[J].地球科学进展,2005,20(11):2-4.
[2] 刘欢,张柏楠,王开强.我国载人小行星探测任务规划[J].国际太空,2013,(7):27-31.
[3] 高红卫.日本“隼鸟号”航天器探测“丝川”小行星[J].航天工业管理,2006,(1):40-41.
[4] 孙林,鲍金河.航空成像光谱仪的发展和在侦查中的应用[J].遥感信息,2010,(6):115-119.
[5] 杜述松,王咏梅.空间应用干涉成像光谱仪的研究[J].光学仪器,2008,30(3):77-82.
[6] Roger R E.Lossless Compression of AVIRIS Images[J].IEEE Transactions on Image Processing,1996,5(5):713-719.
[7] Tamara G.Kolda,Brett W.Bader,Tensor Decompositions and Applications[J].SIAM Review,2009,51(3):455-500.
[8] F.L.HITCHCOOK,The Expression of a Tensor or a Polyadic as a Sum of Products[J].Journal of Mathematics ans Physics,1927,6(1):164-189.
[9] 周欣.粒子群算法在图像处理中的应用研究[D].武汉:湖北工业大学,2011:10-12.
[10] 张培强,柴焱,张晓玲,等.基于波段分组的3DSPIHT 高光谱图象无损压缩算法[J].中国图象图形学报,2005,10(4):4.

