距离走动补偿优化及FPGA实现
马婷婷, 李毓琦, 成思文
(上海无线电设备研究所,上海200090)
0 引言
雷达探测远距离径向运动目标时,发射脉冲串信号,然后对回波进行长时间相参积累,再对每个距离门的回波信号进行多普勒滤波,以提高对微弱目标的探测能力[1]。然而对于高速运动目标而言,目标相对于雷达的径向运动会引起回波包络在脉冲重复周期内发生走动。例如目标径向速度为600m/s,雷达的距离门为75m,在1s的积累时间内目标跨越8个距离门,造成目标能量分散在很多个距离单元中。直接按距离门进行FFT 时,信噪比损失严重,相参积累性能下降。因此,在相参积累前,需要对距离走动进行补偿,使回波包络对齐。
本文在分析距离走动原理的基础上,针对常用的目标回波包络补偿算法普遍运算量较大的问题,提出了抽取移位补偿方法,避免了运算冗余,减少了运算量和处理时间。
1 常用距离走动补偿方法
PD 雷达发射一长串线性调频脉冲。发射脉冲的脉宽为Tp,调频速率为γ,载频为fc,忽略对后续相参积累没有影响的时频耦合项[2],则第m个脉冲的基带回波为
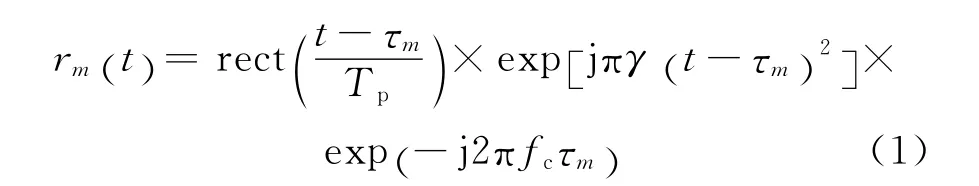
式中:τm为第m 个脉冲的延迟。
设目标离雷达的初始位置为R0,径向速度为v,则第m 个脉冲到达时刻,目标与雷达之间的距离为Rm=R0+vmT,则
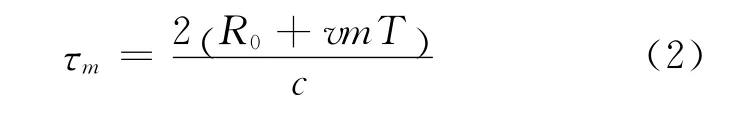
式中:T 为雷达发射脉冲重复周期。
对目标基带回波进行脉冲压缩后,得
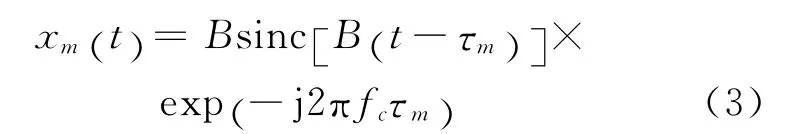
式中:B 为信号的带宽,B =γTp。从式(3)可以看出,脉冲压缩后的信号包络呈sinc函数,且中心位于τm处。
由式(2)和式(3)可知,对于运动目标,径向速度导致每个脉冲回波延迟τm不一样,每个脉冲压缩后信号包络的中心位置也不同,即发生了包络走动。
从慢时间维看,将会导致目标能量分散,幅度降低,主瓣展宽,获得的信噪比很差,不能从杂波中检测目标。因此,需要对回波信号进行距离走动补偿,使得包络在慢时间维对齐。
包络走动补偿是在离散化后完成的。此时进行移动是以采样周期为单位的,若目标的回波真实延迟是采样周期的分数倍,则会产生补偿误差。
常用的补偿算法有包络移位插值、频域校正法和Keystone变换法[3]。
(1)包络移位插值法
包络移位插值法是对目标回波进行线性插值重构,然后进行时域移位使回波包络对齐。为了减少运算量,一般将线性插值和移位合并处理。包络移位插值法的优点是可以一次性补偿分数阶的延迟差,但是,在采样值较多的情况下,插值运算使得移位的运算量大大增加。
(2)频域校正法
频域校正法是在数字频域脉冲压缩时,在频域上乘以延迟因子,补偿各个脉冲之间的包络走动差。但是,在窄带系统中,频域脉冲压缩处理的运算量和复杂度都大于时域脉冲压缩处理。
(3)Keystone变换法
Keystone变换法是将回波变换到快时间维上进行插值,再做慢时间尺度变换,以校正回波跨距离单元的走动。需要对脉冲压缩后的信号在快时间维进行傅里叶变换,再对频域信号进行慢时间维尺度变换。在积累脉冲数较多的情况下运算量较大。
2 抽取移位补偿方法
雷达积累处理系统框图,如图1所示。
常用距离走动补偿在抽取降采样之后实现。本文将抽取降采样和距离走动补偿合并处理,构建抽取移位补偿方法。基于抽取移位补偿法的雷达系统框图,如图2所示。
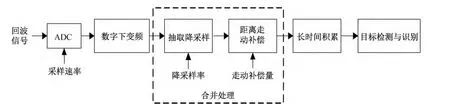
图1 雷达积累处理系统
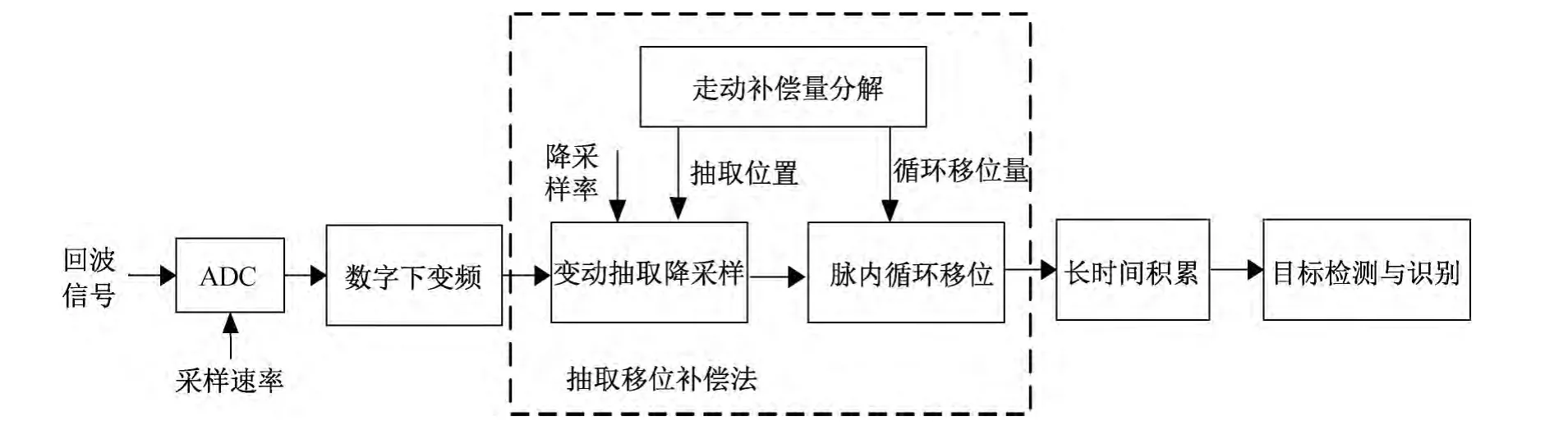
图2 基于抽取移位补偿法的雷达积累处理系统
传统意义上抽取降采样对离散信号固定位置抽取,对抽取后的信号序列补偿[4]。抽取移位补偿方法是将抽取降采样与距离走动补偿重新统筹,分成变动抽取和脉间循环移位两部分完成走动补偿。
将数字下变频后的信号看成一组横向序列,变动抽取降采样是指不同组的信号序列抽取位置是动态的,脉内循环移位是在同一脉冲内,将抽取后的信号进行移位处理。因此,抽取移位补偿方法的核心是根据距离走动量推导出变动抽取位置以及循环移位量。
2.1 补偿参数设计
处理机对回波在快时间维进行采样,每个回波采样点数为N,接收到M 个回波脉冲后,按矩阵方式排列,横向为快时间维,纵向为慢时间维。若长时间积累,目标回波包络就会发生走动,需要补偿,保证目标回波能量聚集在同一个距离单元,提高相参积累后的信噪比。
设采样信号经过数字下变频后为sm(n),距离走动校正后信号为ym(n),抽取倍数为L,则
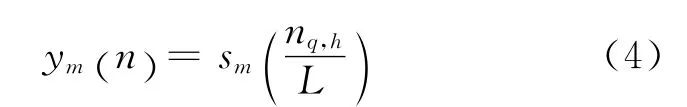
如图3所示,斜线点表示对回波采样,采样率为fs。距离走动,信号分散在不同距离门内。距离走动补偿是将信号集中到同一距离门内并L倍抽取,得到补偿后的信号,如水平线点表示,信号集中在第0 号距离门,速率为fs,L,fs=L×fs,L。将分散在第i号距离门的信号映射到第0号距离门,需补偿掉距离走动量ΔRm。
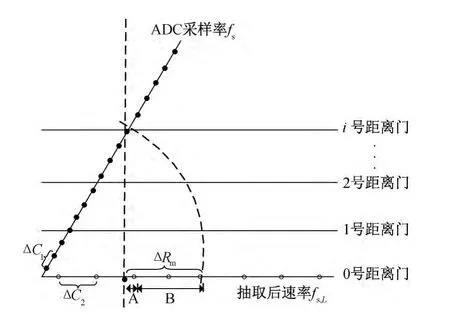
图3 距离走动补偿示意图
一般目标的回波真实延迟并不是采样周期的整数倍,若只是以采样周期为单位进行移位,必然会造成补偿误差。采用小数补偿和整数补偿两部分来减少小数阶延迟带来的损失。整数补偿以抽取后信号周期为单位进行移位,余下的由小数补偿完成。采样率fs是抽取后信号速率fs,L的L倍,从L 个点中选取1个离目标最近点作为小数补偿后的值。可见,小数补偿同时完成了抽取工作。
整数补偿需在同一组脉冲内部完成移位补偿,称为脉内循环移位补偿,设定移位参数为h;小数补偿从L 个点中抽取靠近目标最近点时,每次抽取位置不同,称为变动抽取位置补偿,设定抽取参数为q。如图3 所示,需补偿的走动量由小数补偿量A 与整数补偿B两部分组成。因此,根据走动量计算出参数q、h值是完成距离走动补偿的关键。
设ADC采样时距离分辨单元为ΔC1,抽取后距离分辨单元为ΔC2,弹目径向速度为v,由式(4)可得

当前脉冲周期内距离走动量为ΔRm,那么脉内循环移位补偿的移位参数为
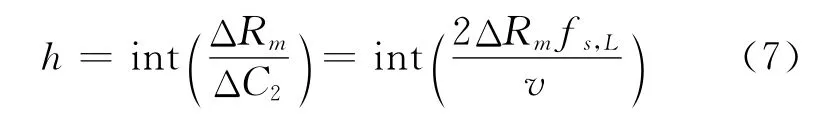
式中:int(·)表示取整。
信号点按照移位量h 移位后,将总的走动量减去整数阶移动量,余下的走动量以变动抽取位置补偿,抽取参数为
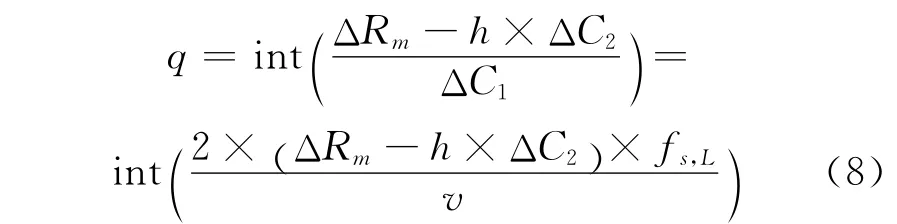
脉冲内的回波信号看成一组序列,从每L 个点中取第q 个值,再按h值进行移位,重新排列后的信号会聚集在同一距离门内,完成走动补偿。
2.2 抽取移位补偿的FPGA设计
FPGA 内置丰富的BlockRAM 存储资源,并具有并行流水快速实现算法功能的优势。根据计算整数阶移位补偿及小数阶抽取补偿方法,在FPGA 中给予映射并实现。
小数阶主要是根据抽取位置q不同来实现补偿,整数阶主要是根据移位量h 来实现对齐。整个算法实现主要分成控制模块、双口RAM 存储模块以及补偿参数计算模块。FPGA 做校正的模块框图如图4所示。
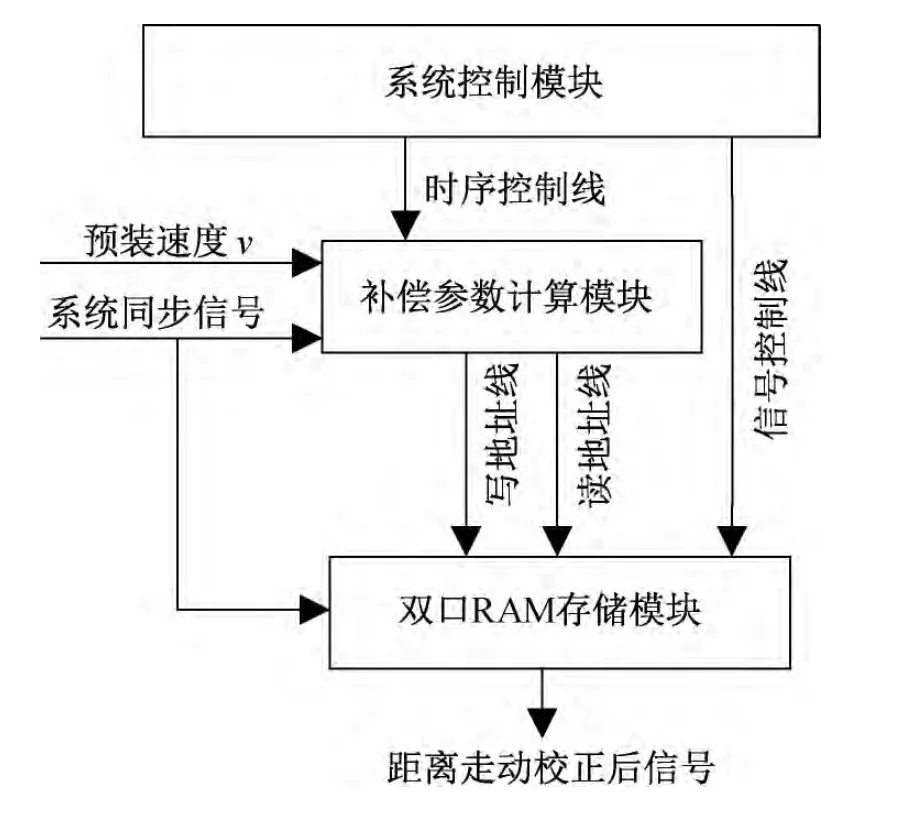
图4 校正模块框图
控制模块是用状态机来控制整个系统数据流向以及各个模块时序状态;双口RAM 存储模块是缓存小数阶补偿并抽取后的数据,最终根据控制信号输出不同起始地址数据,对缓存中的数据进行移位输出,得到距离补偿后的数据;算取参数补偿模块是以一个脉冲周期为时间单位,并乘以当前速度v,来进行算取距离走动量,结合以上给出的公式,计算出小数阶补偿抽取位置q 和整数阶循环移位量h。FPGA 实现流程图如图5所示。
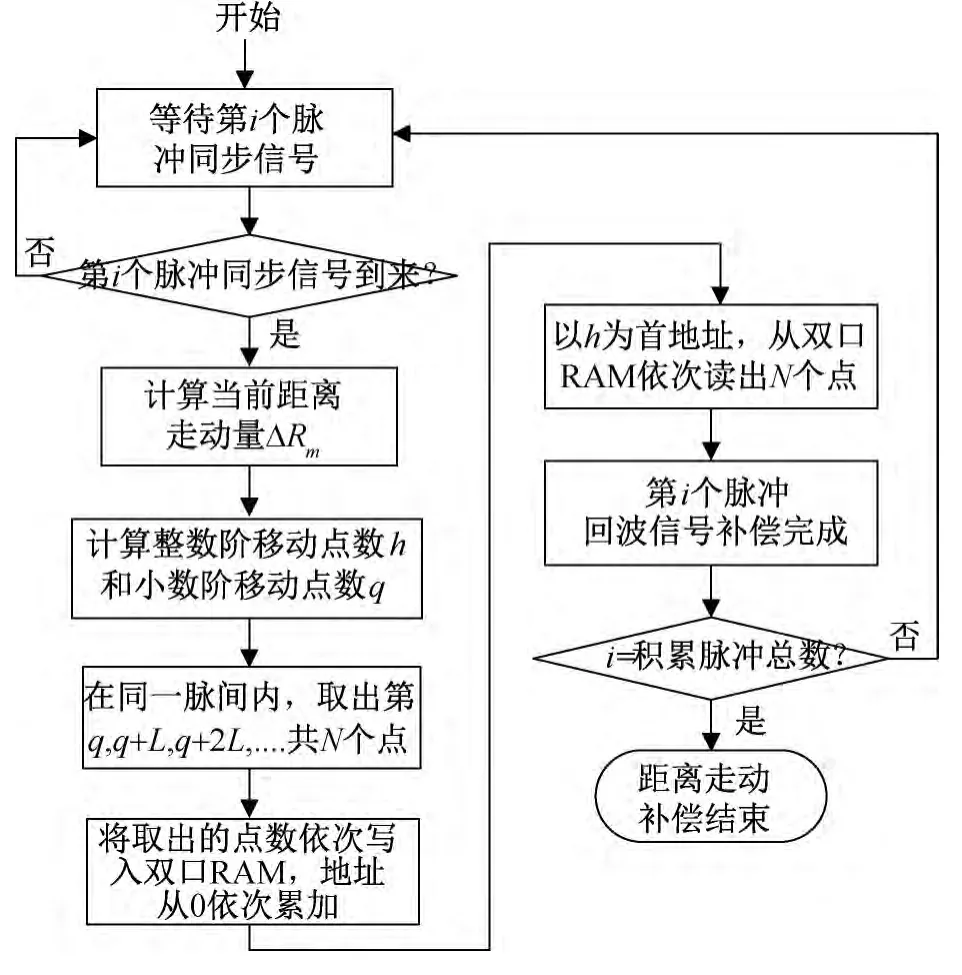
图5 距离走动补偿FPGA 实现流程
为了保证一个脉冲周期内的数据在当前周期进行循环移位而不会被移到相邻脉冲之中,采取以下做法:当以h为首地址读取双口RAM 时,若读到尾地址,则循环到0地址继续读取,直到读取到h-1地址。这样循环读取数据N 点数据即表示本脉冲周期内距离走动补偿完成。
2.3 抽取移位补偿的FPGA设计
由式(7)和(8)可见,在计算q以及h 时,需要使用乘法器和除法器,在FPGA 中可以调用乘法器和除法器的IP 核。计算距离走动量需要1个乘法器IP核,流水延时3个时钟周期;计算h 值时需1个乘法器IP 核,并有3个时钟流水延迟;算取q值时需1个乘法器IP核和一个除法器,至少有6个时钟流水延迟。
重新分析公式,计算q 以及h 可以看成是距离走动量对fs,L求商、求余,并余数对以fs求商的过程。
考虑到fs及fs,L均为2的幂次方,在计算这两个参数时可以进行优化,求余求商的过程用减法器以及移位过程来替代,流水延时2个时钟周期。具体对比结果,如表1所示。
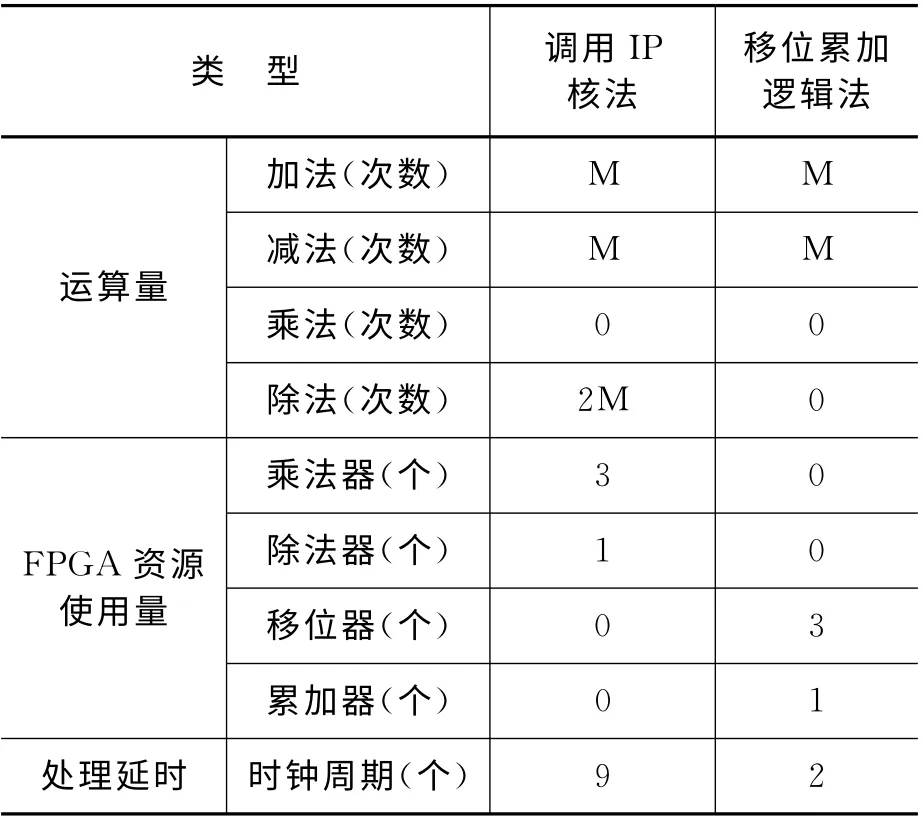
表1 优化前后资源、运算量及延时对比
可以看出,原调用IP核来计算参数的过程就可以转换为采用简单的移位累加逻辑来实现,这在FPGA 中不仅可以节省使用资源,还可以减少结果输出延时。
3 实测结果分析
为了验证此种距离走动补偿实现方法的性能,将此模块应用到探索一代项目中,在长时间积累前进行距离走动补偿。雷达接收机输出中心频率为60 MHz、带宽为2 MHz的中频信号。考虑到信号带宽远小于中心频率,采用带通采样技术,以降低成本,便于后续处理,选用ADC 采样率fs为16 MHz。
为了满足输出信号速率大于等于原信号带宽,以8倍进行抽取,抽取以后信号速率fs,L为2 MHz。一个脉冲周期内有512个距离波门,积累脉冲周期为1 024个。在雷达导引头工作前,由系统预定装置速度为8km/s。
FPGA 采 用XilinxVirtex5 的XC5VSX95T器件,在ISE平台综合实现。将FPGA 补偿后的结果通过RapidIO 接口实时送入DSP,并将数据导入Matlab中进行分析对比。补偿前后脉冲相对位置,如图6所示。
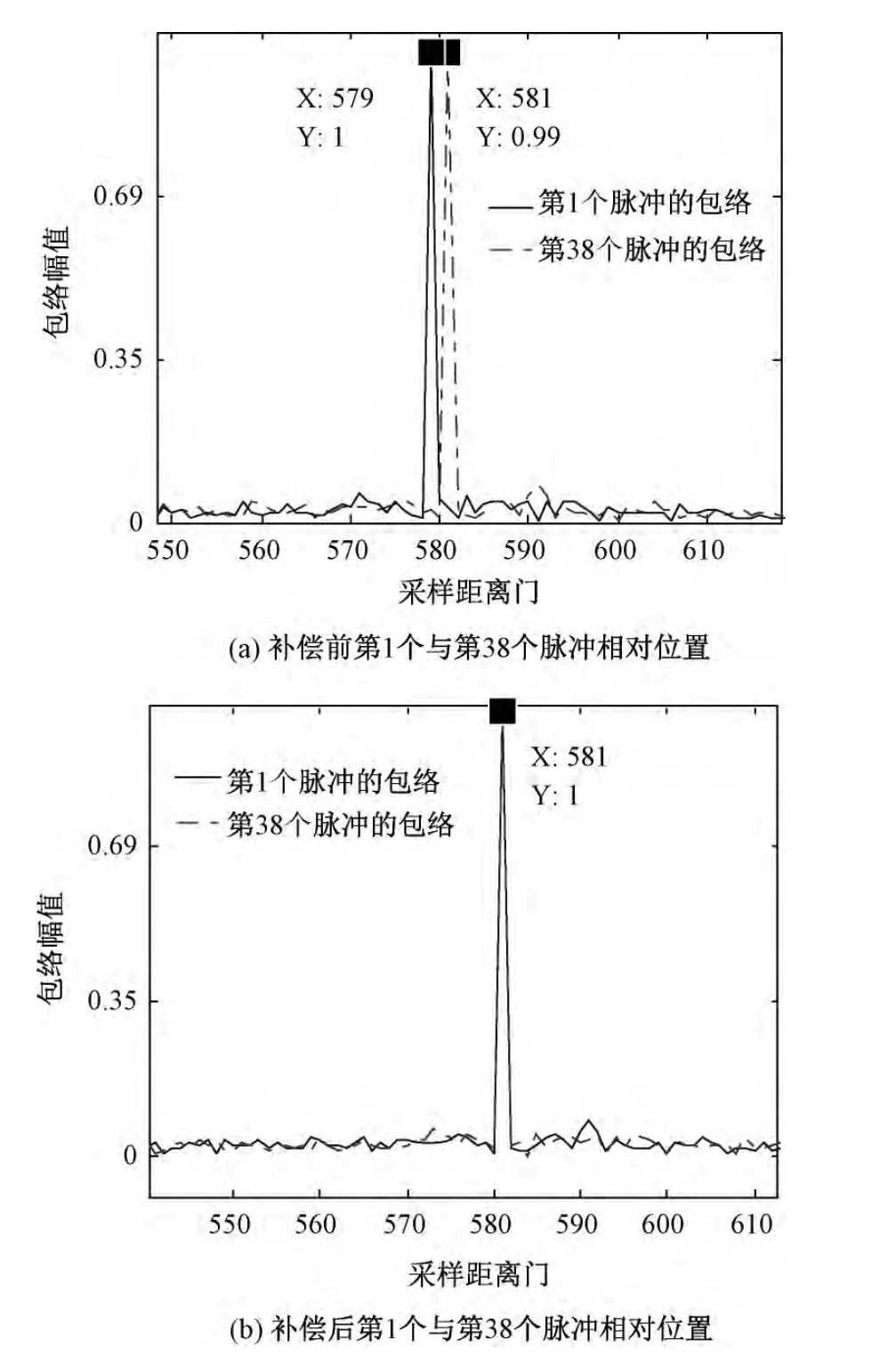
图6 补偿前后脉冲相对位置对比图
以第1个回波的脉冲包络与第38个回波的脉冲包络为例进行对比,补偿前,距离走动现象如图6(a)所示,相对走动了2个距离门。经本文提出的抽取移位补偿后,如图6(b)所示,在第581个距离门内包络重叠,即表示回波在第581个距离门能量达到聚集。
再对补偿前后相参积累结果进行对比,目标静止时信噪比为38.9dB,不补偿距离走动的情况下信噪比为30.6dB,补偿距离走动后的信噪比为38.8dB。
可以发现,采用抽取移位补偿后,回波信号得到了很好的积累,几乎接近于目标静止时的信噪比。
用优化后的结构,对回波进行走动补偿,并进行相参积累。补偿前后的回波时域信号,如图7所示。
可以看出,补偿前各个脉冲能分量散在579、580及581等不同距离门内,随着脉冲积累增多,能量走动越严重,而经过补偿后,能量全部集中在第581个距离门,排列整齐,相参积累做多普勒滤波时,能获得很好的信噪比,可以快速检测到目标位置。
4 结束语
结合实际工程应用特点,本文提出结构简单、易基于FPGA 实现的距离走动补偿的方法,采取小数阶和整数阶分开补偿,取得了良好的补偿效果。
相比于插值移位法,小数阶抽取补偿和整数阶移位补偿大大减小了运算量,实现结构简单。另外对获取补偿所需要的抽取和移位参数的运算进行了优化,进一步减少运算量的同时,节约了乘法器资源,缩短了运算延时时间,提高了系统的实时处理能力。
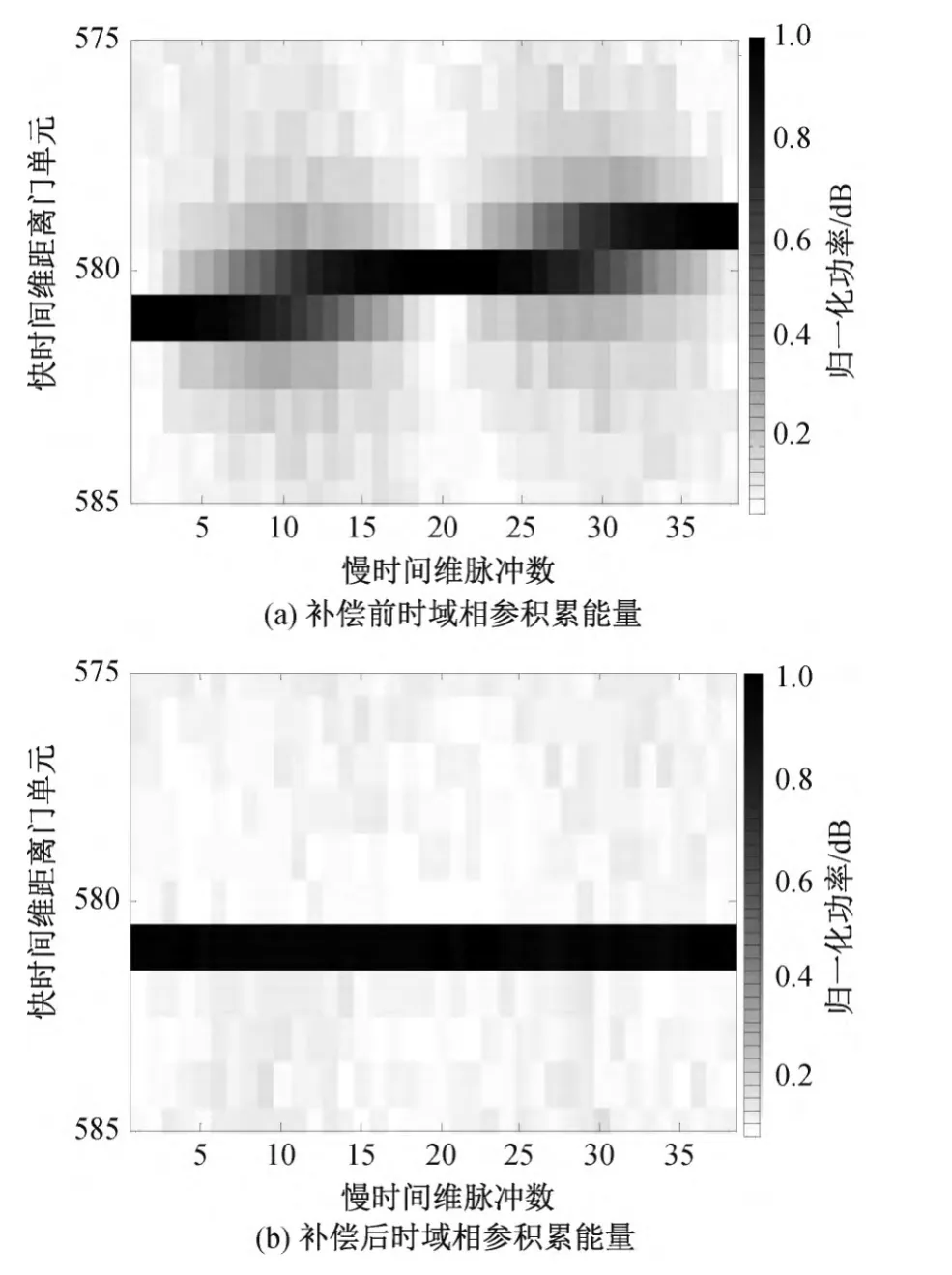
图7 补偿前后时域相参积累能量对比图
[1] 丁鹭飞,耿富录.雷达原理(第三版)[M].西安:西安电子科技大学出版社,2002.
[2] 陈远征,朱永锋,赵宏钟,等.基于包络插值移位补偿的高速运动目标的积累检测算法研究[J].信号处理,2004,20(4):387-390.
[3] 夏卓卿.脉冲多普勒雷达长时间积累技术研究[D].成都:电子科技大学,2010.
[4] D J Rabideau,P Parker,D Rabideau.Ubiquitous MIMO Digital Array Radar[C].Conference Record of the 37th Asilomar Conference on Signals,Systems and Computers,2003:1057-1064.

