基于分数阶域瞬时频率估计的线性调频引信测距性能分析

陶 艳， 郝新红， 岳 凯， 孔志杰

（北京理工大学 机电工程与控制国家级重点实验室，北京100081）

0 引言

线性调频（LFM）引信具有低截获概率、高测距精度等优点，成为无线电引信领域的研究热点［1］。无线电引信的测距精度与其所采用的信号处理方法是分不开的［2］。现有无线电调频引信采用谐波定距法存在与最大调制频偏成反比的固有测距误差，减小的前提条件是增大调制频偏。对于实际的调频引信，考虑到工程可实现性，增大频偏将受到多方面因素的限制，使得固有测距误差难以降低［3］。

分数阶傅里叶变换（FRFT）是一种统一的时频变换，能同时反映信号在时域、频域的信息，尤其在处理LFM 信号方面具有特有的优势［4］。2007年，Kamalesh Kumar Sharma和Shiv Dutt Joshi等提出了基于瞬时频率（Instantaneous Frequency）的FRFT 时延估计方法［5］。而后，岳凯等将该时延估计方法应用于调频引信，在文献［6］中提出了基于分数阶域瞬时初始频率估计和基于分数阶相关的两种定距方法，这两种方法都不依靠谐波信号获取距离信息，较谐波定距方法而言，具有更高的定距精度。

本文从LFM 信号的分数阶域分析入手，研究了基于分数阶域瞬时频率估计的线性调频引信的测距性能，推导了理论测距精度和量化测距精度，分析了测距精度的影响因素，从而为线性调频引信的参数优化设计提供理论依据。

1 基于分数阶域瞬时频率估计的定距原理

本文使用三角波信号作为调制信号，线性调频引信的工作原理如图1所示。首先，压控振荡器产生的载波信号被三角波信号调制后经由功率放大器放大送入定向耦合器，一部分留作参考信号，一部分由天线发射出去；发射信号遇目标后被反射形成回波信号；回波信号经收发共用天线接收后，与载波振荡器产生的纯载波信号混频，经低通滤波器后输出中频信号；同时，作为参考信号的发射信号也与纯载波信号混频、滤波后，输出参考中频信号。而后，对两路中频信号作已知角度的分数阶傅里叶变换，在特定分数阶域上对信号进行最大峰值搜索，求取其分数阶域坐标，获得峰值点位置差。最后，根据分数阶域峰值点位置差换算得到时间延迟，以此计算弹目相对距离来实现定距功能。

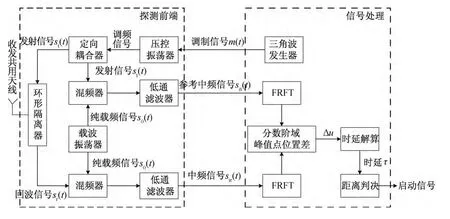
图1 基于分数阶域瞬时频率估计的定距原理框图

分数阶傅里叶变换有一个十分重要的特性：若x（t）为线性调频信号，它在时频平面（t，f）的Wigner分布为一条斜线。如果进行适当的坐标旋转，这条斜线在新的分数阶域坐标系（u，v）下的Wigner分布可能成为平行或垂直于横轴的直线，即所得到的x（t）的FRFT 变换——分数阶域信号Xp（u）是单谐波或冲激函数［7］。三角波调频信号是由两个单分量LFM 信号组成的实信号，而实信号的频谱是对称的，因此它在特定角度的分数阶域上的表现为两个冲激函数，如图2所示。

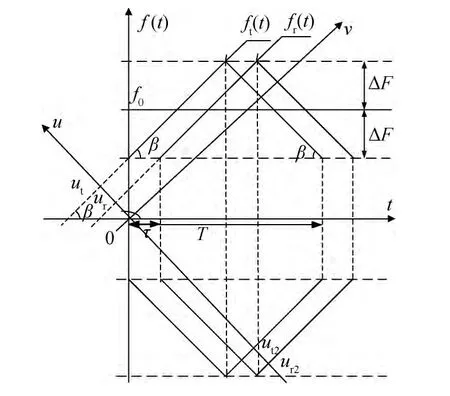
图2 三角波调频信号频率随时间变化图

图2中，ft（t）表示发射信号频率，fr（t）表示回波信号频率，f0为载波频率，ΔF为频偏，T为调制信号周期，调频率β ＝4ΔF／T，延迟时间τ ＝2R／c，R 为弹目相对距离，c是电磁波在空间中的传 播 速 度，α 为FRFT 变 换 的 角 度，ut和ur分 别为分数阶域上发射和回波信号对应冲激函数的横坐标。

从图中可以看出，时延τ 在分数阶域上的投影就是两个冲激函数横坐标ur和ut间的距离，即时域信号ft（t）和fr（t）在分数阶域上对应的冲激函数横坐标间的差值。

图2中发射信号频率可表示为

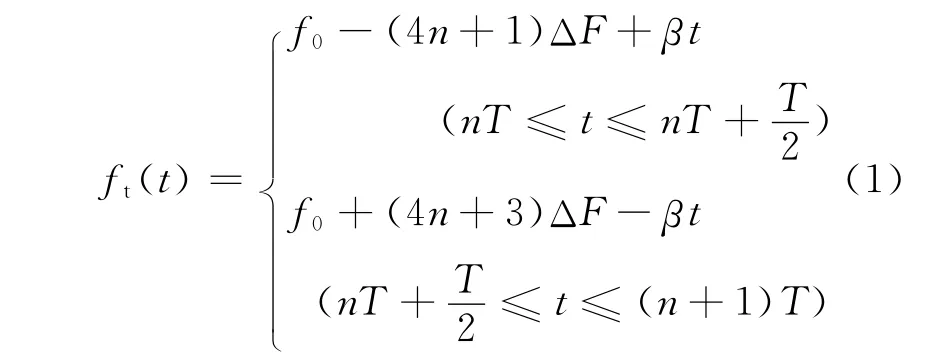
其中，n＝0，1，2，…。

相应的回波信号频率为

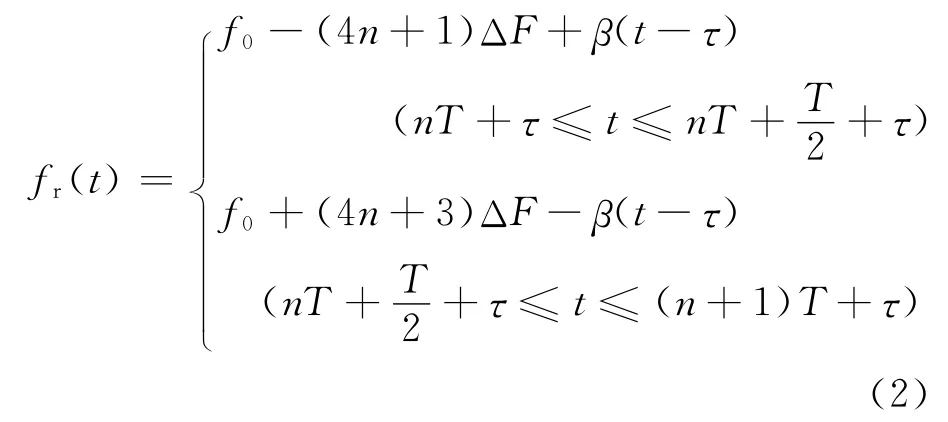
发射信号和回波信号分别和纯载波信号混频、滤波后得到两路中频信号，其所对应的频率分别为

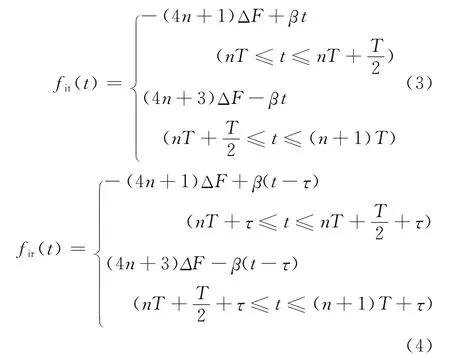
从式（3）和式（4）可以看出，参考中频信号Sit（t）和中频信号Sir（t）满足三角波调频信号条件，在特定的分数阶域具有良好的时频聚集性。对两路中频信号进行固定角度的分数阶傅里叶变换，即

得到特定阶域的分数阶信号，并搜索最大峰值点所对应的u域坐标upt和upr，获得峰值点位置差为

由分数阶傅里叶变换的时移特性可知［4］，时延τ和分数阶域上最大峰值点位置差Δu 的对应关系为

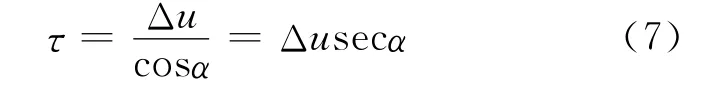
将式（7）代入距离公式进行解算，求出弹目相对距离为

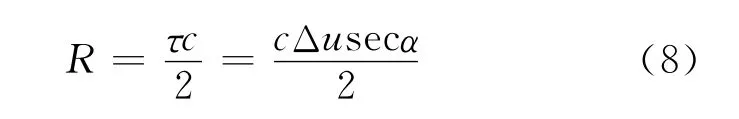
该定距方法利用线性调频信号在特定分数阶域上具有良好的时频聚集性特点，使该体制引信具有较高的定距精度；同时结合调频引信收发相干的特性，和LFM 信号的调频率已知这一先验条件，避免了对最优分数阶傅里叶变换阶数的搜索，使计算量控制在与FFT 相当的水平，满足工程应用的要求。

2 测距精度公式推导及性能分析

2.1 LFM 信号分数阶域分析

由式（3）可知，参考中频信号si（t）为

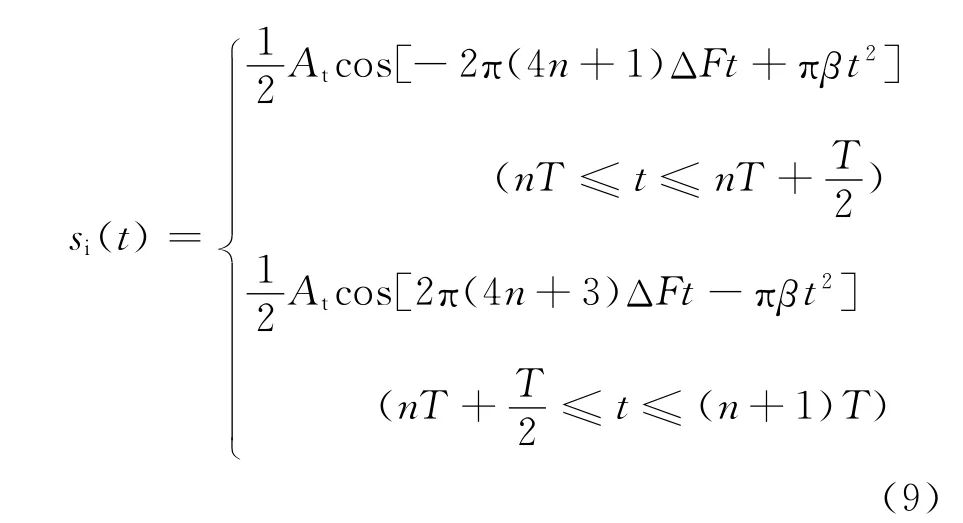
取参考中频信号的一个周期作α角的分数阶傅里叶变换，得到p 阶的分数阶信号为

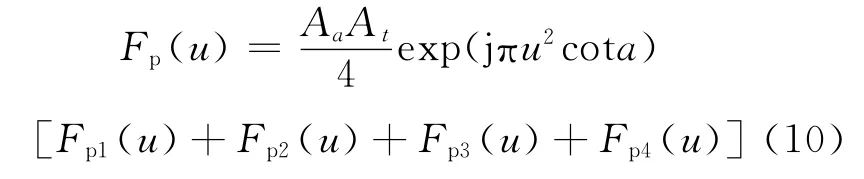
式中：Fp1（u）、Fp2（u）和Fp3（u）、Fp4（u）分别表示sinc函数和菲涅尔积分，具体表达形式为

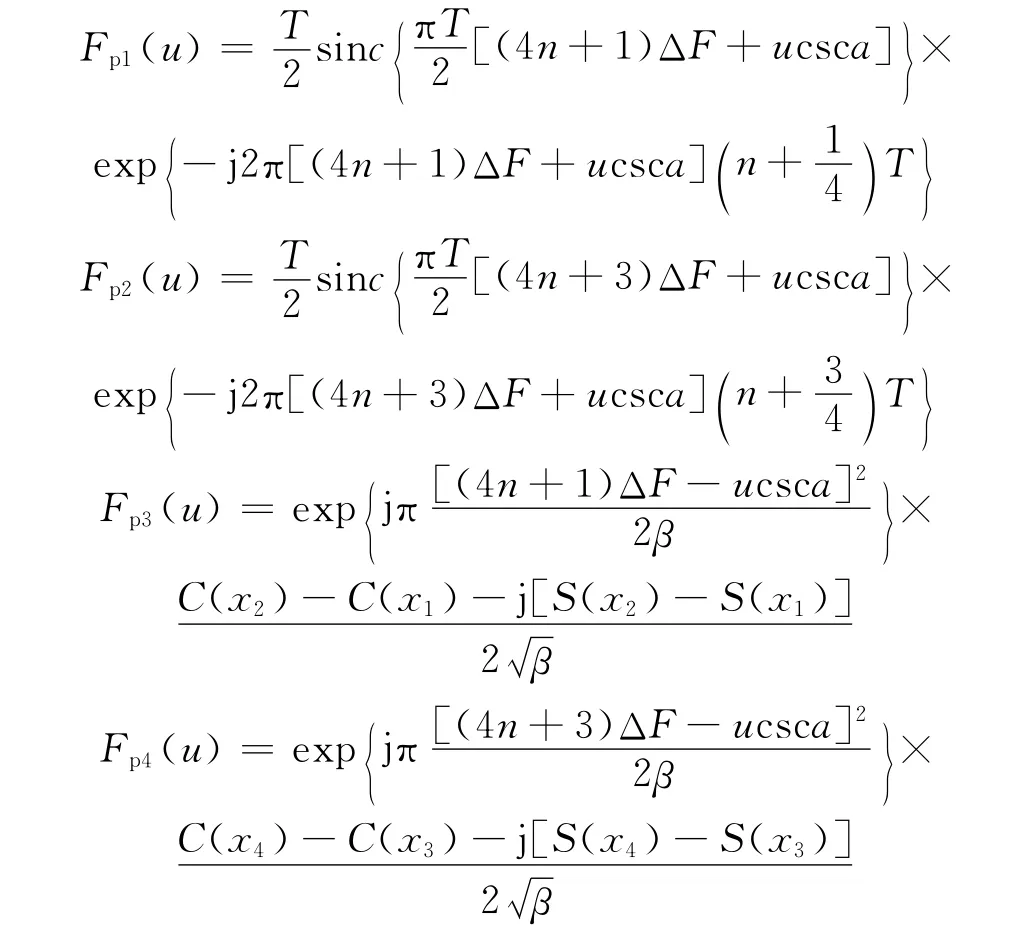
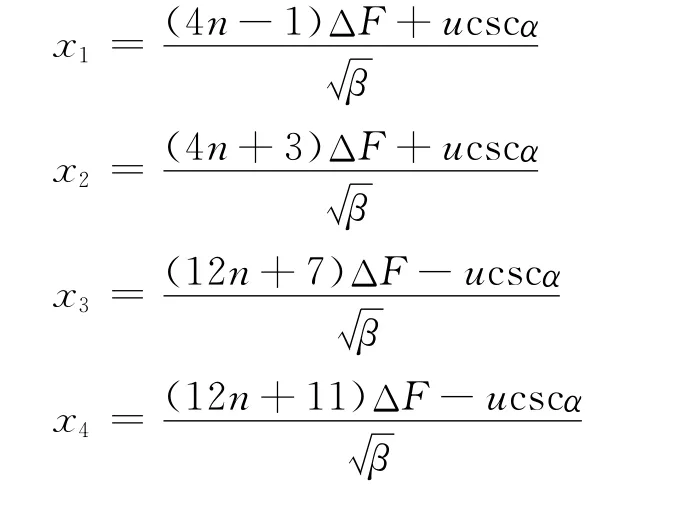
从式（10）可以看出，一个周期内三角波调频信号在分数阶域上表现为两个sinc函数和菲涅尔积分的叠加，并且两个sinc函数主瓣峰值间的距离恰巧是延拓周期uT＝βTsinα 的一半［8］，如图3所示。

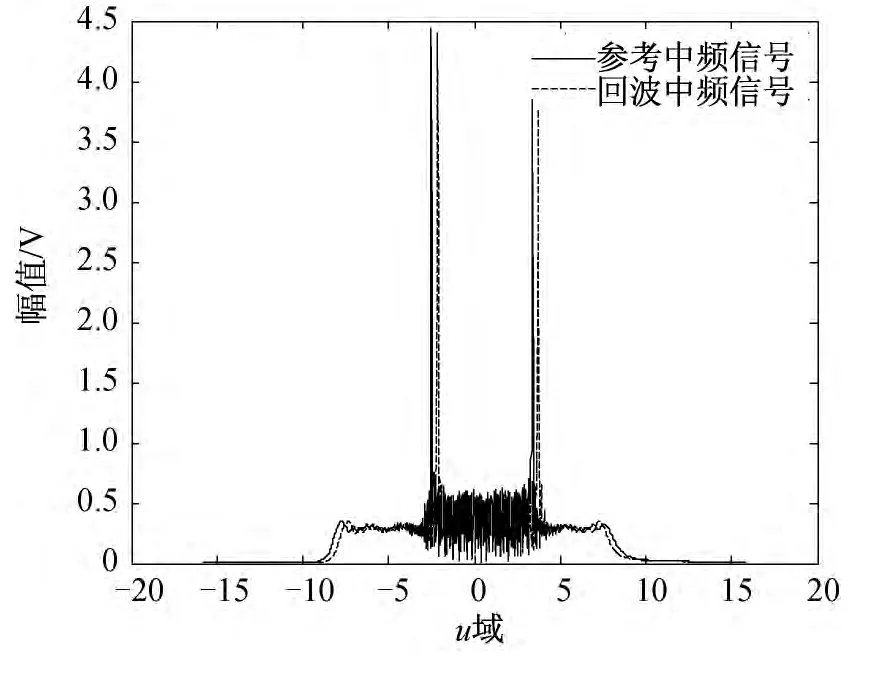
图3 单周期下三角波调频信号的FRFT 结果

因此，多周期下的分数阶信号Fp（u）的sinc函数是以周期uT／2＝βTsinα／2进行延拓的，如图4所示。

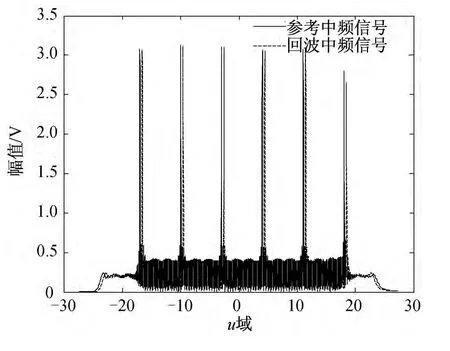
图4 多周期下三角波调频信号的FRFT 结果

2.2 理论测距精度

测距精度可以通过估计时延误差得到［9］，而时延现在是通过获取分数阶域峰值点位置差（即u域延迟误差）计算得到的。因此，估计u 域延迟误差就可以获取测距精度表达式。

由式（10）可知，信号的能量在分数阶域上都集中在sinc函数上，因此可以将分数阶信号简化为sinc函数。通过计算简化后，分数阶信号的距离模糊函数，来估计u域延迟误差，从而得到时延误差。

实际中的分数阶信号并不是无限长的，而是宽度为Tu的观测窗内的信号。为了简化计算，采用宽度为T／2的观测窗，此时简化后的分数阶信号可表示为

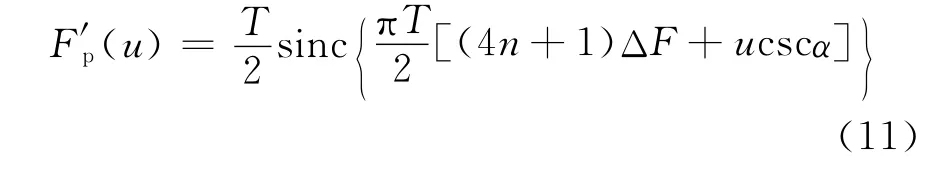
其对应的单周期距离模糊函数为

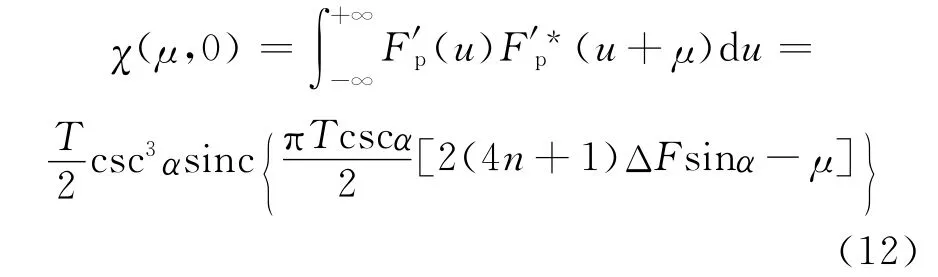
若定义距离模糊函数主瓣6dB 宽度为2us（半电压宽度），以us近似表示分数阶域信号的延迟估计误差［9］：

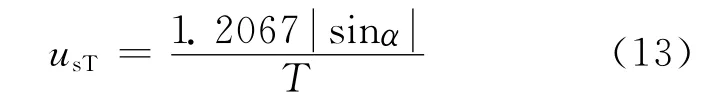
将式（13）代入式（8），可计算得到单周期下的理论测距精度为

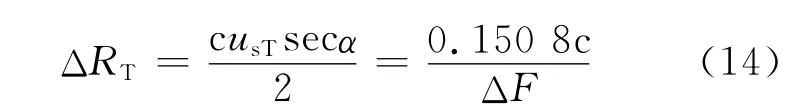
由尺度变换特性可知，若采用宽度为Tu的观测窗（为了信号的完整性考虑，观测窗一般都取周期的整数倍，即Tu＝mT ），则此时的理论测距精度为

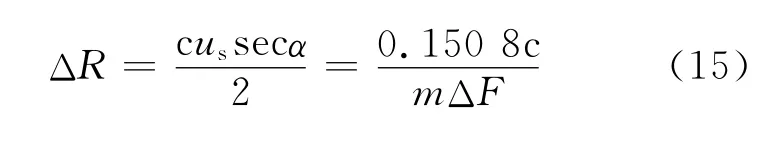
2.3 量化测距精度

在采用DFRFT 进行时频分析时，时域和分数阶域皆离散化。如果用采样频率fs对时长为Tu的时域信号进行采样得到了N 点数据，为时域离散数值集｛δt，2δt，3δt，…，Nδt｝，等效对应于分数 阶 域 离 散 数 值 集 为 ｛δu，2δu，3δu，…，Nδu｝secα，其中δu为分数阶域最小采样间隔，即分数阶域分辨力［10］。分数阶域分辨力δu 决定了实际的距离测量误差［11］，本文为了和前面的理论测距精度作区分，称之为量化测距精度。其中有

将式（16）代入式（13），可推导得到分数阶域信号的量化延迟估计误差δu为

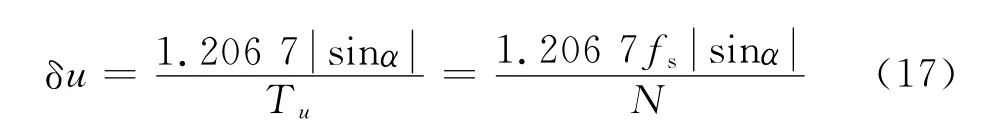
将式（17）代入式（8），可计算得到量化测距精度为

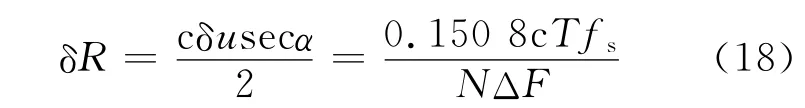
由奈奎斯特采样定理可知，采样频率需要满足fs≥2ΔF，那么量化测距精度可变化为

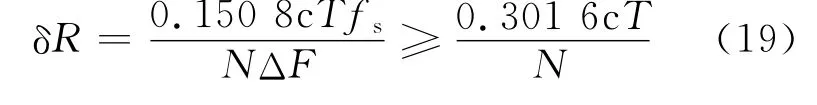
2.4 测距精度的影响因素

在调制频偏为15MHz，调制频率为150kHz，采样频率为150MHz，观测周期为5，观测点数为5 000时，计算得该方法的理论测距误差为ΔR＝0.603 2m，量化测距误差为δR＝0.603 2m。式（18）和式（15）其实是测距精度的两种不同表达形式：从理论测距精度公式可以看出，该方法的测距精度主要受到调制频偏和观测周期这两个参数的影响；从量化定距精度公式可以看出，该方法的测距精度还会受到调制频率和采样点数这两个参数的影响。下面从调制频偏、观测周期、调制频率和采样点数这四个参数入手，具体分析测距精度的主要影响因素。

调制频偏是影响引信测距精度的一个固有因素，首先来分析调制频偏的影响。从式（15）可以看出，理论测距精度与调制频偏成反比，测距精度随着调制频偏的增大而提高，如图5所示。而工程可实现性限制了调制频偏的提高［3］，则可以在不增加调制频偏的前提下，通过改变其他参数来提高引信的测距精度。

观测周期是影响引信测距精度的另一个主要因素。从式（15）可以看出，理论测距精度与观测周期成反比，测距精度随着观测周期的增大而提高，如图6所示。

观测周期太小，测距精度太低，不可取；观测周期太大，对测距精度的影响不大，反而会增加计算量，影响实时性，也不宜取；因此，观测周期应取2～7之间，这样既能保证有比较好的测距精度，又不会带来太大的计算量。

从量化定距精度式（19）可以看出，调制周期也是影响测距精度的一个因素，量化测距精度和调制周期成正比，和调制频率成反比。而综合式（16）进行考虑，可以发现实际影响测距精度的是观测周期，而调制频率对其没有影响，如图7所示。

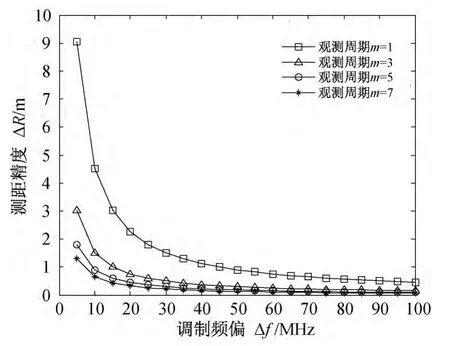
图5 调制频偏对测距精度的影响

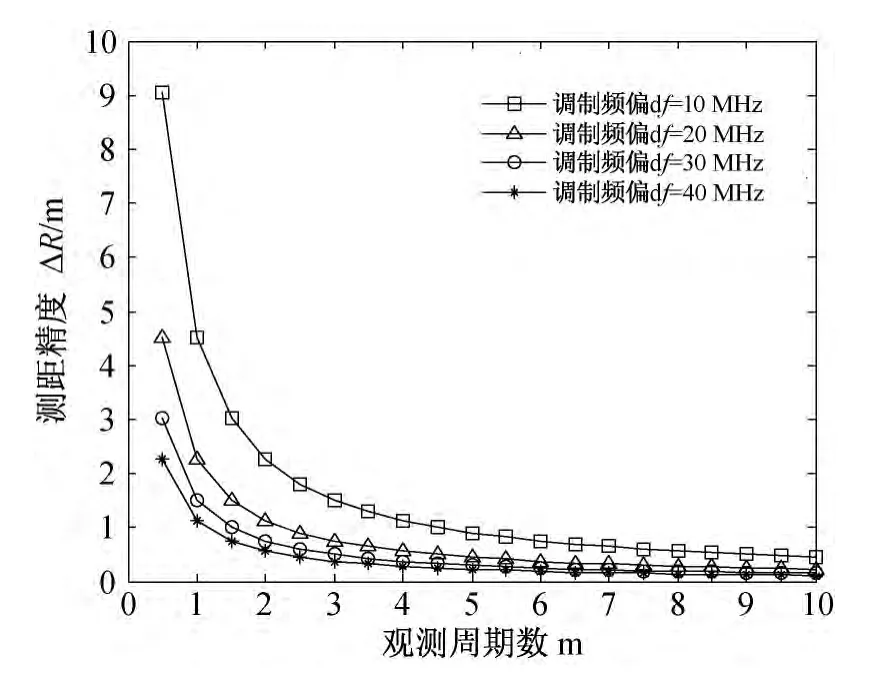
图6 观测周期对测距精度的影响

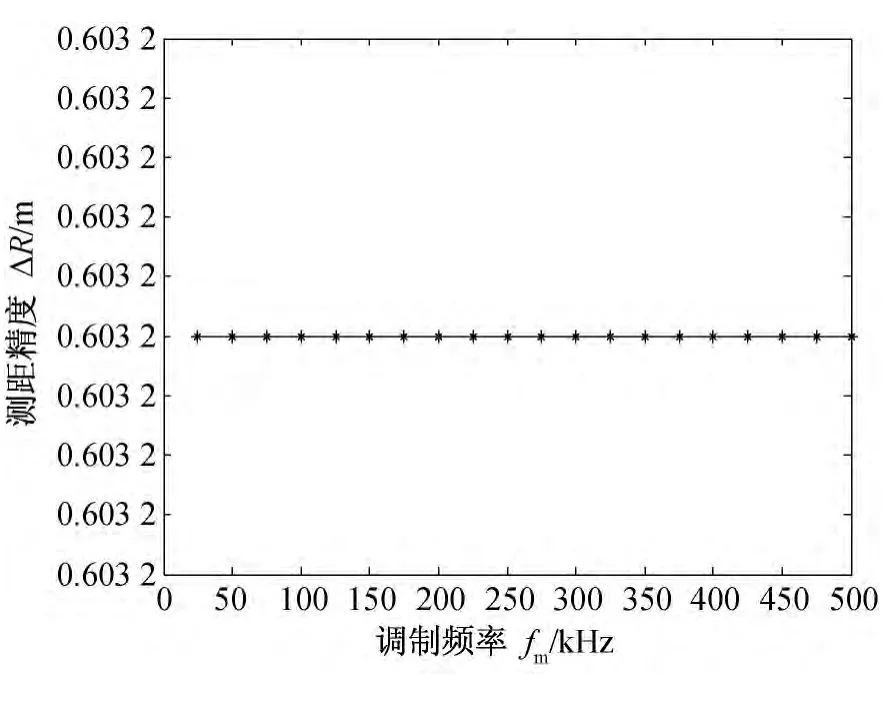
图7 调制频率对测距精度的影响

从式（19）可以看出，采样点数是影响测距精度的另一个因素，且量化测距精度和采样点数成反比。综合式（16）进行考虑，发现实际上影响测距精度的还是观测周期，当观测周期一定时，采样点数对测距精度没有影响，如图8所示；而当采样频率一定时，采样点数体现观测周期的时候，才会引起测距精度的相应变化。

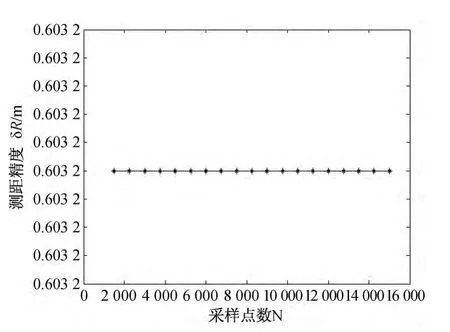
图8 采样点数对测距精度的影响

由文献［3］可知多普勒频率fD和时延τ的对应关系为

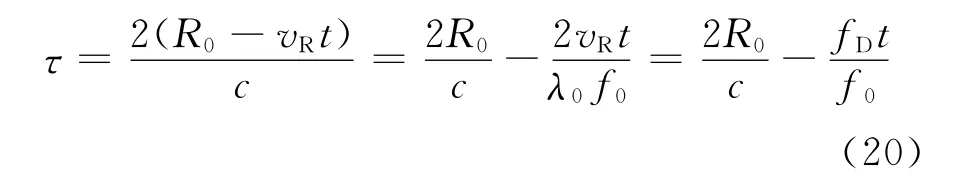
该定距方法直接估计时间延迟，而时延本身就包含多普勒频率，无法将其剔除。且多普勒频率多存在低频段，而载频多使用射频段，将其代入式（20），可发现多普勒频率对时延τ的影响可忽略不计。

通过对调制频偏、观测周期、调制频率、采样点数和多普勒频率这五个参数对测距精度的影响分析，发现测距精度主要取决于调制频偏和观测周期，而不受调制频率、采样点数和多普勒频率的影响，且相比较而言，调制频偏和观测周期对测距精度的影响相当。因此，可以在不提高调制频偏的前提下，通过选取合适的观测周期来达到提高测距精度的目的。

3 结论

本文研究了基于分数阶域瞬时频率估计的线性调频引信的测距性能。首先对线性调频（LFM）信号进行分数阶域分析，并以模糊函数为工具推导测距精度的理论定距精度和量化定距精度，在此基础上分析测距精度的影响因素，并仿真得到以下结论：基于分数阶域瞬时频率估计的线性调频引信的测距精度主要取决于观测周期和调制频偏，调制频率、采样点数和多普勒频率对测距精度没有影响；测距精度随调制频偏的提高、观测周期的增大而提高；工程可实现性限制了调制频偏的提高，观测周期的增大带来了计算量的负担，因此该方法可以在不提高调制频偏的前提下，合理选择观测周期来改善调频引信的测距精度。该结论可以为基于分数阶域瞬时频率估计的线性调频引信的参数优化设计提供理论依据。

［1］ 向程勇，潘曦，王正浩，等.基于求导比值的调频连续波测距方法［J］.兵工学报，2014，35（5）：613-619.

［2］ 李玉清.近20年来国外导弹引信技术研究与发展概况［J］.制导与引信，2002，23（3）：1-8.

［3］ 赵惠昌.无线电引信设计原理与方法［M］.北京：国防工业出版社，2012.

［4］ 陶然，邓兵，王越.分数阶傅里叶变换及其应用［M］.北京：清华大学出版社，2009.

［5］ Sharma K，Joshi S.Time Delay Estimation Using Fractional Fourier Transform［J］.Signal Processing［serial online］，2007，87（5）：853-865.

［6］ 岳凯，郝新红，栗苹，等.基于分数阶傅里叶变换的线性调频引信定距方法［J］.兵工学报，2015，36（5）：801-808.

［7］ 孙晓兵，保铮.分数阶Fourier变换及其应用［J］.电子学报，1996，（12）：60-65.

［8］ 黄宇，刘锋，王泽众，等.基于周期FRFT 的LFMCW 信号检测与参数估计［J］.中国科学：信息科学，2014，44（4）：498-510.

［9］ 郝新红，白钰鹏，崔占忠.一种复合调制波形的测距性能分析［J］.北京理工大学学报，2008，28（4）：297-301.

［10］ 邓兵，王旭，陶然，等.基于分数阶傅里叶变换的线性调频脉冲时延估计特性分析［J］.兵工学报，2012，33（6）：764-768.

［11］ 周刚，傅佑麟，徐振方.LFMCW 数字化测距测速的分辨力与精度分析［J］.微计算机信息，2006，22（22）：313-314.