基于LabVIEW软件的时频域测试研究

□ 杨文兴 □ 余 亮 □ 孙旭东 □ 张振生 □ 陈 杰 □ 王瑞平，2

1.宁波吉利罗佑发动机零部件有限公司 浙江宁波 315336 2.浙江吉利罗佑发动机有限公司 浙江宁波 315800

对于信噪比很低的信号，无论从时域或频域都很难将有用信息提取出来，笔者借助短时傅里叶变换的基本理论，将时域和频域联合起来分析，从而来描述信号的频率随时间的变化关系，也可以简单计算出信号的功率谱随时间的变化。但在信号处理中，能得到的信号长度是有限的，需要对无限长的时间序列添加一个窗函数，进而来观察窗函数对时频域联合分析时的影响。

1 时频域测试分析

时频域测试分析是通过信号映射手段实现的，可以将一维时间域信号映射到能量对频率和时间的二维空间中。时频域测试分析能够确定在某一时刻频率成分的分布情况，而频谱能够确定哪些频率存在。但是，短时傅里叶变换可以认为是一种整体变换，只能分析了解信号在时域或频域中的全局特性。对于像汽车车速等非平稳信号，时频域测试分析对了解信号频谱随时间变化的情况，有极其重要的作用。虚拟仪器LabVIEW借助图形化的编程语言，通过图标代替文本行来创建应用程序，采用数据流程编辑方式，程序的执行顺序依据程序框图中节点之间的数据流向来决定，一般情况下，采用图标表示函数，用连线表示数据流向。对于测试仿真软件LabVIEW，可以提供出一个比较优质的功能模块[1]，STFT Spectrogram.vi模块可以计算时频域平面上的信号能量分布情况，观察其某些特定信号的能量在联合时频域里是如何分布的。

2 短时傅里叶变换STFT的基本原理

为了获得多分量信号中各分量的瞬时频率，可以采用局部频谱的概念，在一个很窄的窗函数里取出信号，经过求其傅里叶变换，同时也去除了窗函数以外的信号频谱，使用窄窗函数的傅里叶变换（短时傅里叶变换，STFT），它是加窗傅里叶变换的一种形式，短时傅里叶变换的基本思想是把信号划分成许多小的时间间隔[2]，用傅里叶变换分析得到每一个时间间隔，以便确定该时间间隔内存在的频率，其表达式为：

式中：“*”表示复共轭；g（t）是有紧支集的函数；f（t）是被分析的信号。

在这个变换中，e-jwt起着频限的作用，g（t）起着时限的作用。随着时间t的变化，g（t）所确定的“时间窗”在t轴上移动，使f（t）逐渐进行分析。具体变换如图1所示。

测试程序所编写的时频联合分析模块为短时傅立叶变换分析块，短时傅里叶变换频谱图能够反映信号能量的频谱随时间的变化情况，即信号的能量在时频平面中的分布。程序的前面板可以显示参数部分、短时傅里叶变换时频平面图以及瞬时频谱图。短时傅立叶变换模块的流程图如图2所示。

▲图1 短时傅里叶时频变换图

▲图2 短时傅里叶变换程序流程图

▲图3 车速信号的时频分析程序框图

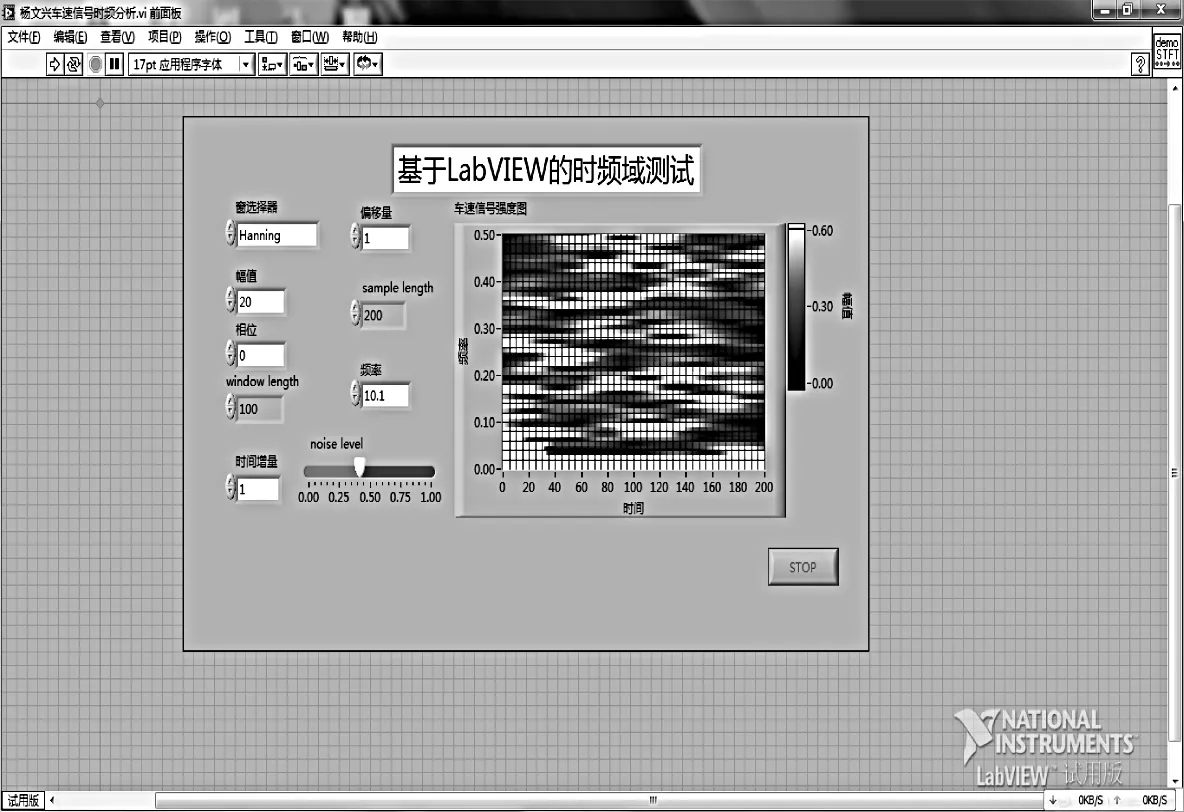
▲图4 海宁窗（窗长度100）车速信号的时频分析运行结果

▲图5 海宁窗（窗长度200）车速信号的时频分析运行结果

▲图6 汉明窗（窗长度100）车速信号的时频分析运行结果

▲图7 汉明窗（窗长度200）车速信号的时频分析运行结果

3 非平稳汽车车速信号的实例分析

对于汽车车速等一些非平稳信号[3]，可以通过虚拟仪器LabVIEW中最经典的短时傅里叶变换，将汽车车速信号映射在二维强度图上，横、纵坐标分别表示时间和频率[4]。

窗函数选择海宁窗（Hanning），仿真汽车车速信号时，选择幅值为20，偏移量为1。为了使有用信息避免泄漏及流失，选择海宁窗的长度为100，采样长度为200，基于LabVIEW的汽车车速信号时频分析测试程序框图及运行结果如图3、图4所示。

当窗函数选择海宁窗（Hanning）时，窗口长度选为200，其它参数不变，车速信号的时频分析结果如图5所示。

当窗函数选择为汉明窗（Hamming）时，采样长度为200，窗口长度为100，其它参数不变，则车速时频分析运行结果如图6所示；采样长度为200，窗口长度为200，其它参数不变，则车速时频分析运行结果如图7所示。

比较图4、图5的运行测试结果，同时选择海宁窗，不同的窗长度，选择长度为200的分辨效果好于选择100的，时频域复合图线条相对比较明晰；比较图5、图 7，选择窗长度均为200，选择窗函数为海宁窗，其运行测试效果更加明显。

从图4～图7可以看出窗函数的长短和类型对短时傅里叶的影响，采用汉明窗的效果不如选择海宁窗，若选择同一函数，窗函数的长度为200，优于长度为100的，包括在时频域有更好的分辨率，能够使其分析结果更加准确，选择的窗函数长度太短，频域上扩展的能量集中性就不是很好，所以在短时傅立叶变换中窗函数的选择起着至关重要的作用。

4 结论

借助测试分析软件LabVIEW的测试平台，选择非平稳的汽车车速信号进行时频域分析，对于不同形式的信号，要选择合适的窗函数，包括窗函数的类型和长度，可以得到很好的分析结果，在时频域联合平面中显示了信号时间与频率的变化关系，为以后分析实际信号提供了工具和手段。

[1]邹文，陈爱萍，顾汉明．联合时频分析技术在地震勘探中的应用[J]．勘探地球物理进展，2004，27（4）：246-250.

[2]刘君华．基于LabVIEW 的虚拟仪器设计[M]．北京：电子工业出版社，2003．

[3]张贤达，保铮.非平稳信号分析与处理[M]．北京：国防工业出版社，1998．

[4]臧观建，刘正平．基于 LabVIEW 的联合时频分析[J]．华东交通大学学报，2007，24（4）：121-124.