运行计划约束下的动态可达性分析与计算
郭建媛,贾利民,秦 勇
(北京交通大学a.交通运输学院;b.轨道交通控制与安全国家重点实验室,北京100044)
运行计划约束下的动态可达性分析与计算
郭建媛a,贾利民*b,秦 勇b
(北京交通大学a.交通运输学院;b.轨道交通控制与安全国家重点实验室,北京100044)
在城市轨道交通中,随着各条线路的末班车按运行计划逐站完成载客任务,路网上OD两点间的可达路径逐渐变少,直至两点间不可达,这样的路网服务能力随时间的动态变化,称为动态可达性.本文研究运行计划约束下的路网动态可达性计算方法,以支持末班车开行的优化,实现搭乘末班车出行乘客目的地可达的最大化.本文首先分析了末班车开行带来的动态可达性,给出了最晚可达时间、路径可达性、OD可达性定义.在此基础上,提出了末班车开行下路网可达性的计算方法与最晚可达时间求解的递归算法.最后,以路网可达性最大为目标,将可达性计算方法应用于末班车换乘衔接优化.通过算例分析验证了可达性计算方法的有效性.
城市交通;可达性;衔接方案;城市轨道交通;末班车
1 引 言
可达性经常被用来衡量交通系统中的服务提供能力或者达到某地的便捷性,可达性指标反映了去往不同地点的交通运输系统的服务水平[1].可达性可以指从一个车站到达目的车站的便捷程度[2],也可以指路网上OD之间能否到达[3].
随着末班车的运行,路网上两点间的可达路径在逐渐变少,直至两点不可达.这样的路网服务能力随时间的动态变化,本文称之为动态可达性.不同的运行计划,将带来不同的可达性变化,从而影响路网的服务水平和乘客的出行质量.
近年我国已有学者开始对末班车造成的OD间可达性进行研究.罗钦等人[3]分析了列车运行计划开行带来的OD动态可达现象,提出通过优化列车运行衔接和信息发布来提高出行目的地可达;江志彬等[4]提出了时间窗约束下的OD可达性计算方法,给出OD间的可达状态与可达路径的推算流程;徐瑞华等[5]提出末班车衔接优化方案来提高换乘可达性.已有研究在为可达性在末班车开行优化的应用打下基础,但目前的研究无论是从可达性的分析定义,还是其在衔接优化方面的效果,都有待进一步研究.
本文在已有研究的基础上,进一步分析动态可达性内涵特征,以提高路网服务能力为目标,给出适用于末班车开行优化的可达性定义与计算方法.
2 可达性分析
2.1 可达性相关定义
OD间的载客服务随时间的动态变化反映了运行计划影响路径可达和OD可达的过程.在已有可达性定义的基础上,本文结合站点间服务能力随运行计划的变化特点,做出了更进一步的扩充,包括路径可达性,OD可达性.
路径可达性指经特定路径能否从O到达D;此处使用途径车站的有序集合 <O,S0,…,Sn,D>(n≥0)表示路径R;使用FR表示路径R的可达性,当FR=1时表示路径R可达,当FR=0时表示路径不可达.假设OD间的所有物理联通的路径的集合为ASOD,对于任意路径R(R∈ASOD),FR会随时间发生从1到0的阶跃变化.
在此定义FR从1到0跃变的时间点为路径R的最晚可达时间,用TLR表示,当乘客不晚于TLR到达O点站台(后续将到达O点站台的时间称为待发时间,使用TAO表示),则可搭乘列车经路径R到达目的地,当乘客待发时间晚于TLR,则错过路径R上的末班车,无法经路径R到达D.FR与待发时间关系如式(1)所示.
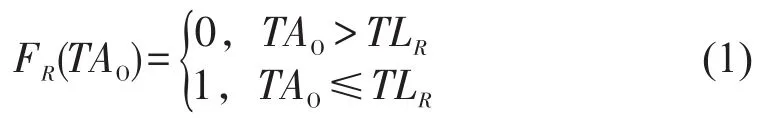
OD可达性指能否从O通过路网到达D,及其可达的便捷程度.使用FOD表示OD间可达性,当FOD=0时表示OD不可达,当FOD>0时表示OD可达,其计算如式(2)所示.
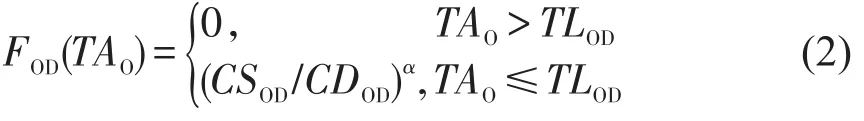
式中 TLOD表示OD的最晚可达时间,当乘客待发时间晚于TLOD,则通过OD间的任何路径都无法到达目的地D,待发时间不晚于TLOD,则存在物理联通且可达的路径R(FR=1⋂R∈ASOD)可以从O到达D;CSOD表示OD之间各条物理路径均可达时,其中的平均成本最小的路径(简称静态最优路径)所对应成本;CDOD表示OD之间实际可达的路径中的成本最小的路径(简称动态最优路径)所对应成本;α为可调节的参数.人们日常出行倾向于选择静态最优路径,当受到运行计划约束出现部分路径不可达的情况,则更愿意选择动态最优路径.
2.2 末班车对可达性的影响
对于OD之间无需换乘的路径,乘客搭乘末班车一定可以到达目的地,而对于OD之间需要换乘的路径,乘客搭乘末班车能否到达目的地受到末班车间换乘衔接的影响[3].
如图1所示,S1和S2是换乘站,A、B、C是中间站,L1和L2为双向线路,图中箭头方向是线路下行方向,使用L11L12L21L22分别表示两条线路的上下行,则存在四个换乘方向:L11-S1-L21、L21-S2-L11、L22-S1-L12和L12-S2-L22.

图1 换乘衔接示例Fig.1 Example of connections
当搭乘末班车在换乘方向L11-S1-L21上可以衔接时,则搭乘末班车在换乘方向L21-S2-L11无法衔接;当搭乘末班车在换乘方向L22-S1-L12上可以衔接时,则搭乘末班车在换乘方向L12-S2-L22无法衔接.因此,末班车开行会带来换乘衔接间的互相约束,进一步在不同路径的可达性之间产生相互约束.
以从A到B为例,存在两条可能的路径:R1:A-S2-B和R2:A-S1-C-B,仅当L22-S1-L12和L12-S2-L22均无法衔接时,R1和R2均不可达,AB间不可达.因此,换乘无法衔接时路径不可达,但OD之间不一定不可达.
假设存在某段时间[T0,T1],L12-S2-L22无法衔接,但L22-S1-L12可以衔接时,则经由路径R2可以到达B,而经由R1无法到达B,此时 R2为[T0,T1]时段内的AB间的动态最优路径.在此时间段内从A仍然能够到达B,出行成本会产生变化,即OD可达性在大于0的情况下数值发生变化.
3 末班车开行下的路网可达性计算方法
3.1 路网可达性计算方法
路网向乘客提供的服务能力既与目的地能否可达相关,又与到达目的地所消耗的成本相关,当乘客出行对应的FOD数值越大,则说明路网向乘客提供的服务能力就越好.因此,定义路网可达性来衡量路网向乘客提供的到达目的地的便捷程度,其计算用式(3)表示.
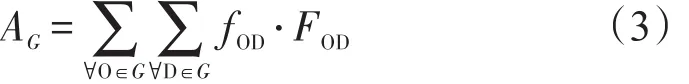
式中 G表示路网站点集合;fOD表示从O去往D的客流量.
可以用末班车开行下的路网可达性ALG来衡量末班车衔接效果,计算用式(4)表示.
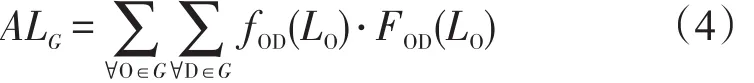
式中 LO表示从O点出发的末班车发车时间.
3.2 末班车开行下的路网可达性计算流程
为了计算得到式(4)中的ALG,主要求解流程如下:
步骤1 加载路网物理结构GS、运行计划TG和OD间的客流量 fOD;
步骤2 计算所有 CSOD和 TLOD(O∈GS, D∈GS,O≠D);
步骤3 每一对OD,当LO>TLOD则FOD(LO)为0;否则,计算TLOD时刻的CDOD,根据式(2)计算得到FOD(LO);
步骤4根据式(4)计算得到ALG.
步骤2中,对OD的最晚可达时间的求解是关键步骤,在后续展开说明,步骤3中对动态最优可达路径的计算,可以参考时刻表约束下的分支定界方法[6,7]求解.
3.3 OD的最晚可达时间计算方法
已有的OD最晚可达时间计算方法[3,4]是在备选路径的停站列表已知情况下匹配时刻表得到结果.但当备选路径不能覆盖所有物理联通路径时,可能使结果出现偏差.
为了更加高效并准确地求解OD间最晚可达时间,本文在列车运行计划和网络拓扑共同约束下,以节点与线路关系集合为基础,采用递归的方法快速求解准确的OD最晚可达时间.
节点与线路关系集合包括后继线路集合和后继节点集合.定义在O点可以搭乘列车出发的线路为后继线路,后继线路集合为LS(O),集合中的元素表示为Li,其中i为线路编号;定义从O点出发沿后继线路可以到达的第一个节点为后继节点,用N(O)i表示O点在线路Li上的后继节点,后继节点集合为NS(O).
定义TLOD(i)为O在后继方向i上的最晚可达时间,即从Li线路出发的最晚可达时间,则可用式(5)来表达OD最晚可达时间与后继方向最晚可达时间的关系,其中OD间的最晚可达时间是从O沿各后继线路出发到达D的最晚可达时间的最大值.
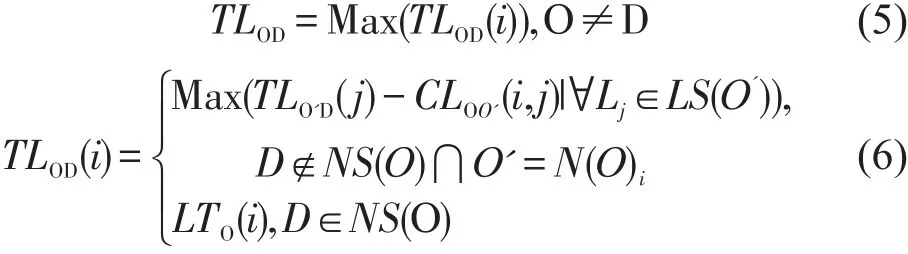
式中 CLOO'(i,j)表示从O点沿线路i到达线路 j上的O'点的消耗成本,O'是O在线路i上的后继节点;TLO'D(j)表示O'在方向 j上的最晚可达时间;LTO(i)表示O点沿路径i开往D的末班车在O点的发车时刻.
D不是O的后继节点时,TLOD(i)为O'在各方向的最晚可达时间与O到O'的成本差值中取极大值;当D为O的后继节点时,TLOD(i)为O点在方向i上的末班车发车时刻.
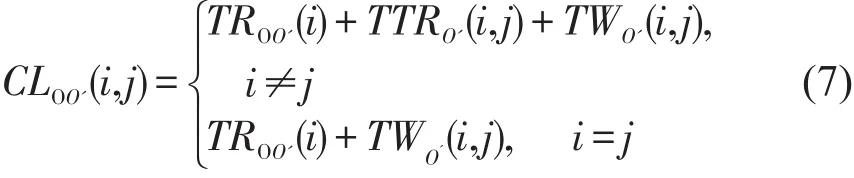
式中 TROO'(i)表示线路i上O到O'的运行时分;TTRO'(i,j)为在车站O'从线路i换乘到线路 j的走行时间;TWO'(i,j)表示在车站O'的等待时间.
当i和 j不相等时,TWOO'(i,j)表示换乘线路带来的候车时间;当i和 j相等时,TWOO'(i,j)表示列车在车站O'的停站时间或终到O'时换乘列车带来的候车时间.TWOO'(i,j)的求解如式(8)所示.
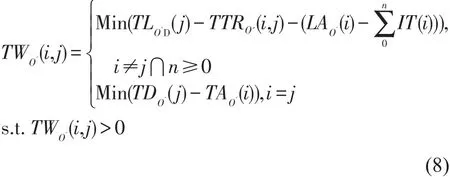
更进一步,对路网中所有OD间的最晚可达时间求解可利用递归求解过程中产生的中间结果TLO'D,减少重复计算.
4 可达性计算在末班车衔接优化中的应用
4.1 应用流程
根据3.1中的计算流程,在路网物理结构和OD间客流已定的情况下,输入不同的运行计划将得到不同的可达性结果,据此可以使用路网可达性对运行计划进行评价.而末班车衔接方案在运行计划制定中具有重要作用[5,9],现有的末班车衔接优化从主观判断[9]或从换乘客流量出发进行优化[5].
在此,结合前述的可达性计算方法,使用路网可达性最大为目标进行末班车衔接方案优化,其应用流程如图2所示.其中,运行计划制定的其他条件包括:线路末班运营时限、区间运行时分、停站时分等,路网物理结构包括车站、线路关系及换乘时间等.
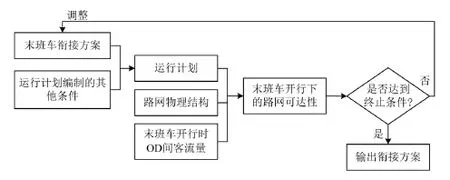
图2 可达性应用流程Fig.2 Flow of applying accessibility
4.2 算例分析
仍以图1为背景,假设路网末班车运营时限为23:00,区间运行时间均为5 min,换乘时间均为2 min,停站时间均为30 s,末班车开行时OD间客流量为
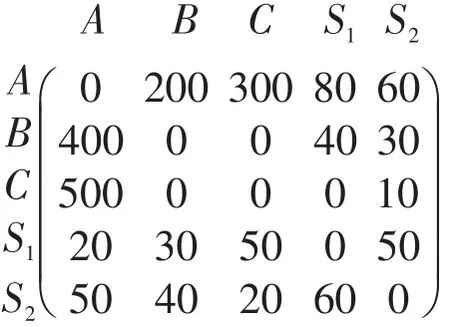
根据OD间的客流量可以得到四个换乘方向
L11-S1-L21、L21-S2-L11、L22-S1-L12和 L12-S2-L22的客流量分别为:500,200,300和400.根据文献[5](方法1)和本文中提出的方法(方法2)分别计算末班车换乘衔接方案,其中路网可达性计算参数α取1,以旅行时间来衡量路径成本,两个方法计算得到的最优末班车衔接方案和末班车开行下的路网可达性数值对比如表1所示.两种不同的方法求解得出不同的衔接方案和路网可达性数值.当以路网可达性为衡量指标时,方法2优于方法1.

表1 衔接优化方案对比表Table 1 Com parison of connection schemes
5 研究结论
本文分析了末班车开行引起的城市轨道交通路网动态可达性特征,给出了路径可达性、OD可达性的内涵说明及最晚可达时间的定义;提出了适用于路网服务能力评价的路网可达性计算公式,和末班车开行下的路网可达性计算方法,并将之应用于末班车衔接优化方法,通过算例分析,本文提出的方法有利于求出更优的末班车衔接优化方案,提高路网服务能力.
[1]Lawrence D Burns,Thomas F Golob.The role of accessibility in basic transportation choice behavior[J]. Transportation,1976,5(2):175-198.
[2]王伟,刘军,李海鹰,等.铁路网抗毁性分析[J].铁道学报,2010,32(4):18-22.[WANG W,LIU J,LI H Y,et al. Survivability analysis of railway network[J].Journal of the China Railway Society,2010,32(4):18-22.]
[3]罗钦,徐瑞华,江志彬,等.基于运行图的轨道交通网络动态可达性研究[J].同济大学学报(自然科学版), 2010,38(1):72-75.[LUO Q,XU R H,JIANG Z B,et al. Dynamic accessibility of urban mass transit network based on train diagram[J].Journal of Tongji University (Natural Science),2010,38(1):72-75.]
[4]江志彬,徐瑞华,罗钦.基于时间窗约束的城市轨道交通网络动态可达性计算方法[P]:中国,CN 102169512A.2011-08-31.[JIANG Z B,XU R H, LUO Q.Computing dynamic accessibility of urban mass transit network based on time-window[P]:China,CN 102169512A.2011-08-31.]
[5]徐瑞华,李璇.城市轨道交通网络末班车衔接方案的综合优化[J].同济大学学报(自然科学版),2012,40 (10):1510-1516.[XU R H,LI X.Comprehensive optimization for connection scheme of last trains in urban mass transit network[J].Journal of Tongji University(Natural Science),2012,40(10):1510-1516.]
[6]Tong C O,Richardson A J.A computer model for finding the time-dependent minimum path in a transit system with fixed schedules[J].Journal of Advanced Transportation,1984,18,145-161.
[7]M H Poon,S C Wong,C O Tong.A dynamic schedulebased model for congested transit networks[J]. Transportation Research Part B,2004(38)343-368.
[8]Rachel C W Wong,Tony W Y Yuen,Kwok Wah Fung,et al.Leung,Optimizing timetable synchronization for rail mass transit[J].Transportation Science,2008,42(1): 57-69.
[9]徐瑞华,张铭,江志彬.基于线网运营协调的城市轨道交通首末班列车发车时问域研究[J].铁道学报, 2008,30(2):7-11.[XU R H,ZHANG M,JIANG Z B. Study on departure time domain of the first and last trains of urban mass transit network based on operation coordination[J].Journal of the China Railway Society, 2008,30(2):7-11.]
Analyzing and Computing Dynamic Accessibility with Constraints of Schedule
GUO Jian-yuana,JIALi-minb,QIN Yongb
(a.School of Traffic and Transportation;b.State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University,Beijing 100044,China)
When time close to the running of last trains,the number of active routes in urban rail transit will become less and less.The network accessibility changing along with the time is called dynamic accessibility. The method about computing dynamic accessibility is studied,which fits to the planning of last trains and improves the service quantity to passengers who want to take very late or even last trains to their destinations.These definitions are given,such as latest accessible time,route accessibility and OD accessibility.Then,the main steps to compute network accessibility with last trains running is presented,and a recursive algorithm is used to compute the latest accessible time.At last,a flow of applying network accessibility is proposed to optimize the connection scheme of last trains.The example is given to demonstrate the feasibility of the method.
urban traffic;accessibility;connection scheme;urban rail transit;last train
1009-6744(2015)01-0118-05
:U239.5
:A
2014-09-03
:2014-10-16录用日期:2014-11-13
国家“十二五”科技支撑计划课题(2011BAG01B02).
郭建媛(1979-),女,河南人,讲师,硕士. *
:jialm@vip.sina.com

