基于分形期权理论的船舶投资决策研究

李电生,张圣泽

（中国海洋大学 经济学院，山东，青岛266100）

基于分形期权理论的船舶投资决策研究

李电生*,张圣泽

（中国海洋大学 经济学院，山东，青岛266100）

船舶作为航运企业最重要的生产资料，其前期的投资决策分析至关重要.一直以来，船舶投资风险价值的计算是困扰人们的问题之一，实物期权理论与B-S定价模型的发展为其提供了一个解决办法.但B-S定价模型中最重要的假设条件是资产价格波动符合正态分布，这与现实差距较大.本文以分形分布条件代替B-S定价模型中正态分布的假设，建立起分形期权定价模型，并利用BDI价格指数进行实证分析.结果证明BDI对数收益率序列的H指数大于0.5，说明BDI收益具有较强记忆性，呈现尖峰胖尾特征.在此条件下，以传统B-S定价模型计算出的船舶投资实物期权价值大于分形期权价值，说明其高估了船舶投资的管理柔性价值，这会使投资者产生盲目乐观心理，进而增大投资决策风险.

水路运输；船舶投资决策；分形期权；B-S定价模型；BDI

1 引 言

船舶作为航运企业最重要的生产资料，具有投资金额大、回收期长和收益波动性大等特点，因此前期的船舶投资决策分析直接关系着航运企业能否持续发展.传统船舶投资决策以贴现现金流法（DCF）为主，美国航运财务学家Cheng P C[1]最早在《航运业财务管理》一书中研究了投资回收期、内部收益率IRR等会计指标在船舶投资决策中的应用，对资金的时间价值进行了初步研究；其后美国航运专家麻省理工学院教授Frankel E G[2]论述了NPV、IRR等评级指标在航运项目的选择及应用，这也是迄今为止DCF方法中最常用的两个指标.

然而之后学者们逐渐发现DCF法存在重大缺陷，即只考虑到了投资过程中资金的时间价值，忽略了其风险价值.与此同时，实物期权理论开始发展起来，该理论最早由MIT的Stewart Myers[3]提出，后来Dixit和Pindyck[4]在《不确定条件下的投资》中对不确定性环境下实物期权理论在投资决策中的应用进行了详细分析.蒋义青[5]最早将实物期权的思想引入到船舶投资领域，运用二叉树法对船舶的延迟期权、退出期权在离散的年度单位内进行了研究；邵瑞庆[6]利用二叉树法研究了船舶投资中的扩张期权、放弃期权等问题；Helen B Bendall和Alan F Sten[7]则将多叉树模型运用到船舶投资决策中，并将转换期权和复合期权应用到船舶投资评价中.

1973年，美国经济学家 Fischer Black和Myron Scholes共同提出了B-S期权定价模型，为金融期权的定价理论奠定了坚实基础，之后该模型被逐渐运用到实物期权定价理论中.近年来，李耀鼎[8]、杨林达[9]、蒋林[10]等学者分别应用B-S定价模型对连续时间下船舶投资的实物期权计算进行了研究，进一步加强了船舶投资决策方法的科学性与严谨性.

但B-S定价模型中最重要的假设条件是资产价格波动符合正态分布，海运价格可以看作船舶投资的资产价格，而通过对近几年的文献梳理来看，海运价格的波动并不符合正态分布.李耀鼎、宗蓓华[11]以方差比检验方法对BDI指数的随机游走趋势进行了检验,结论拒绝了随机游走假设，说明国际干散货航运市场收益率不符合正态分布.翟海杰、李序颖[12]通过对比不同模型时发现T分布能相对更好地描述BDI指数序列的尖峰厚尾特征.由于正态分布具有运算简单等品质，诸多学者目前并没有放弃这一基本假设，或者只是用T分布等特殊分布形式代替正态分布，因此需要引入新理论对海运价格的波动规律进行重新刻画，为船舶投资决策提供更符合现实的基础.分形市场概念自Peters在1994提出后，在股票市场得到了广泛应用，部分学者发现，以分形分布替代正态分布能够很好地解释包括市场恐慌和崩溃等问题.由于海运价格同样存在着长期相关性等特点，因此近几年万九文、吕靖等[13]，李电生、万培祥等[14]等学者分别运用不同的方法证明了国际干散货航运市场具有显著的分形特征.

本文在吕靖和李电生等学者的研究基础上，将海运价格的分形分布特征与实物期权投资决策方法结合，建立分形期权定价模型，并选取1999–2013年的BDI指数进行实证分析，从而为我国航运企业船舶投资决策提供更贴近现实的依据.

2 分形期权定价模型建立

在金融期权定价研究中，B-S定价模型是目前应用最广、也是最成功的定价模型，创立和发展该模型的迈伦·斯克尔斯和罗伯特·默顿也由此获得了1997年诺贝尔经济学奖.B-S模型的一般表达式为

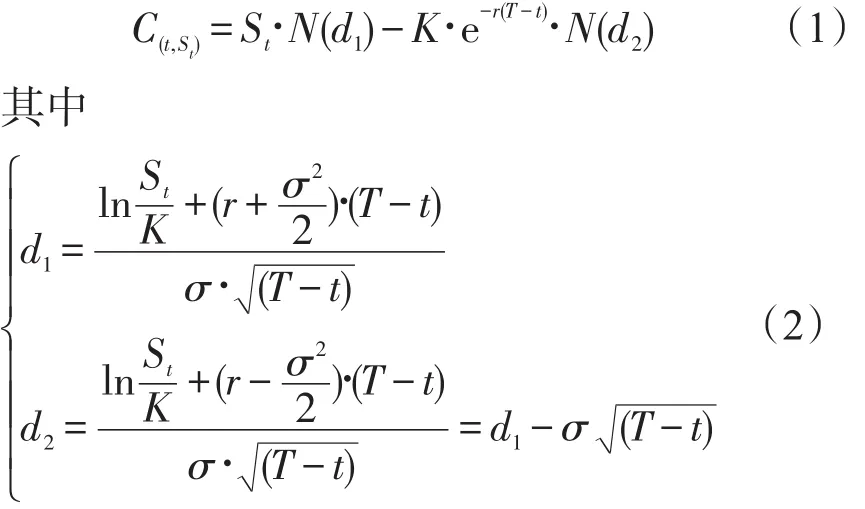
式中 K——期权的执行价格；

r——无风险利率；

St——标的资产的当前价格；

T——期权的到期日；

σ——标的资产收益的标准差，在更广泛意义上作为标的资产价格波动率的度量；

N(g)——标准正态分布的累积密度函数.

由于国际航运市场与金融市场有诸多相似之处，二者都具有市场化程度高、信息透明度高、交易频繁等特点，尤其是干散货运输市场更是创造出与股票价格指数相类似的BDI价格指数.因此李耀鼎[11]、唐友刚等[15]部分学者将国际航运市场假设为与金融市场相类似的有效市场，认为BDI指数和证券价格一样可以反映市场上所有信息，从而将B-S定价模型应用到国际航运市场的资产配置分析中.

但是正如上节所述，B-S定价模型的一个主要假设是资产价格服从正态分布，然而根据吕靖[13]和李电生[14]等学者的研究成果，BDI航运价格指数并不完全服从正态分布，而更符合分形分布.且经过众多学者实证检验，分形分布可以更好地描述时间序列尖峰厚尾和有偏特性.因此本文将B-S定价模型中正态分布假设替换为分形分布假设，从而建立起分形实物期权定价模型.

分形市场中，风险资产价格波动过程满足

式中 μ和σ——常数；

BH(t)——H指数的分形布朗运动，0＜t＜T；

t=0时资产初始价格S(0)=S0＞0.可以解出，资产价格满足

由以上模型可看出，分形B-S定价模型引入了Hurst指数这一指标，这有利于反映资产价格波动的长期记忆性，从而可以更准确计算期权价格.

3 实证分析

3.1 海运价格波动的分形结构检验

（1）数据选取.

本文选取波罗的海干散货指数（BDI）作为研究对象，BDI指数由世界上历史最悠久的航运市场——波罗的海航交所发布，是谷物、钢材、煤炭、矿石等原物料的运费指数.这些物料的需求状况与全球经济荣枯息息相关，因此干散货指数可以看作是全球经济领先指标和晴雨表.由于波罗的海航交所在1999年以国际波罗的海综合运费指数（BDI）取代了BFI，因此本文选取1999–1–5至2013–8–30的BDI数据进行研究，如图1所示.

首先用公式R=logPt-logPt-1将原始价格指数转化为对数收益率序列，结果如图2所示.

图1 BDI日原始价格指数波动图Fig.1 The original fluctuations figure of BDI price index

图2 BDI日对数收益率序列波动图Fig.2 The logarithmic return series fluctuations rate of BDI price

（2）BDI对数收益率序列分布结构检验.

为了检验BDI指数的分布结构，首先对图2中原始数据概率分布曲线与正态分布概率分布曲线进行拟合，结果如图3所示.

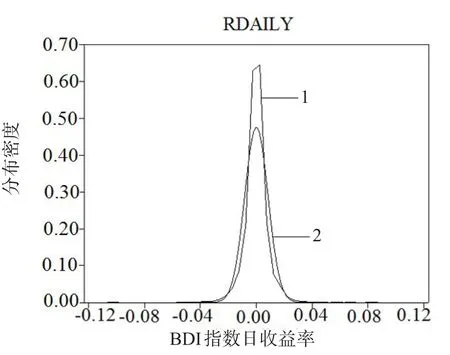
图3 正态分布拟合图Fig.3 The normal fit figure of BDI logarithmic return series

由图3可以直观看出BDI指数具有明显的尖峰厚尾特征，而正态分布不能很好地体现这一特征，二者的拟合效果并不好.表1为BDI指数对数收益序列的正态分布检验结果.

由表1可以精确看出BDI对数收益序列的JB检验和KS检验对应的P值均为0，显著不服从于正态分布，因此若以对数正态分布的假设对BDI对数收益序列进行处理，必将产生较大的误差.本文进而采用STABLE4.0软件以最大似然估计法对BDI指数进行分形分布的估计，本版本较以前有所改进，能够在0.1≤α≤2范围内保持计算结果的稳定性，但是当α＜0.1时，参数估计结果会存在明显问题.表2为估计结果.

表1 BDI指数对数收益序列正态分布检验结果Table 1 The normal test results of BDI index return series

表2 分形分布参数估计结果Table 2 The results of fractal distribution parameter estimation

根据表2结果可知，1999–01至2013–08的BDI对数收益率序列数据的α=1.341 8＜2，表示该序列有明显尖峰厚尾的特点，1＜α＜2，表明分形分布的总体均值存在，总体方差不存在；α≠1且 β=-0.029 67，说明分布右偏且右偏程度不明显；γ指数体现了分形分布的宽度，相当于正态分布的方差，当分形分布为正态分布时，γ等于正态分布方差的一半；δ指数为分形分布的位置参数，决定分形分布的位置，当分形分布总体均值存在时，δ等于总体均值；H指数即Hurst指数，其与 α指数的关系是.进一步运用PP检验对BDI收益率序列的正态分布和分形分布进行拟合，结果如图4、图5所示.图4和图5中，线1为原始数据概率分布，线2为正态分布拟合结果，线3为参考线.

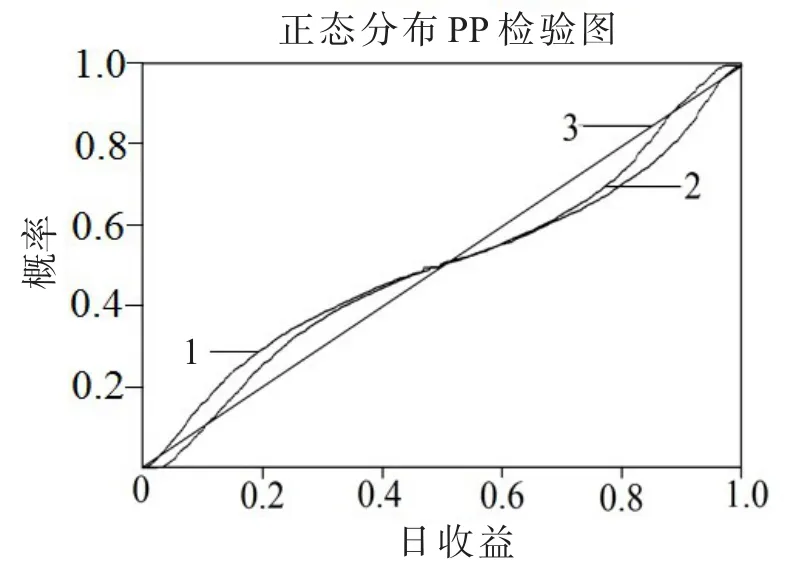
图4 正态分布PP检验图Fig.4 The PP test chart of Normal distribution

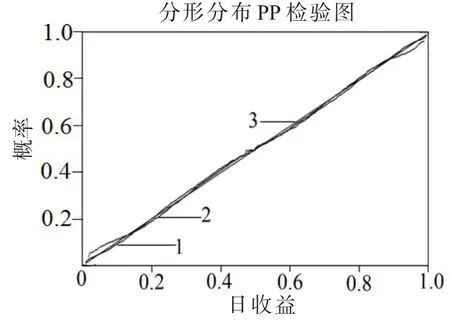
图5 分形分布PP检验图Fig.5 The PP test chart of Fractal distribution

从图5可以直观地看出分形分布的PP拟合曲线与实际概率分布曲线基本一致，而图4正态分布拟合中，正态分布的PP拟合曲线开始在实际曲线下方，之后在实际曲线的上方，说明正态分布会高估低收益率出现的概率，低估高收益率出现的概率.

3.2 分形期权价值计算及影响

实物期权价值实质上是投资的风险价值，即投资之后各种选择权的价值.从上节图4、图5可以看出，相对于分形期权价值拟合结果，传统B-S定价模型计算出的实物期权价值误差较大，以下公式可以进一步精确检验引入H指数对期权价值的影响.

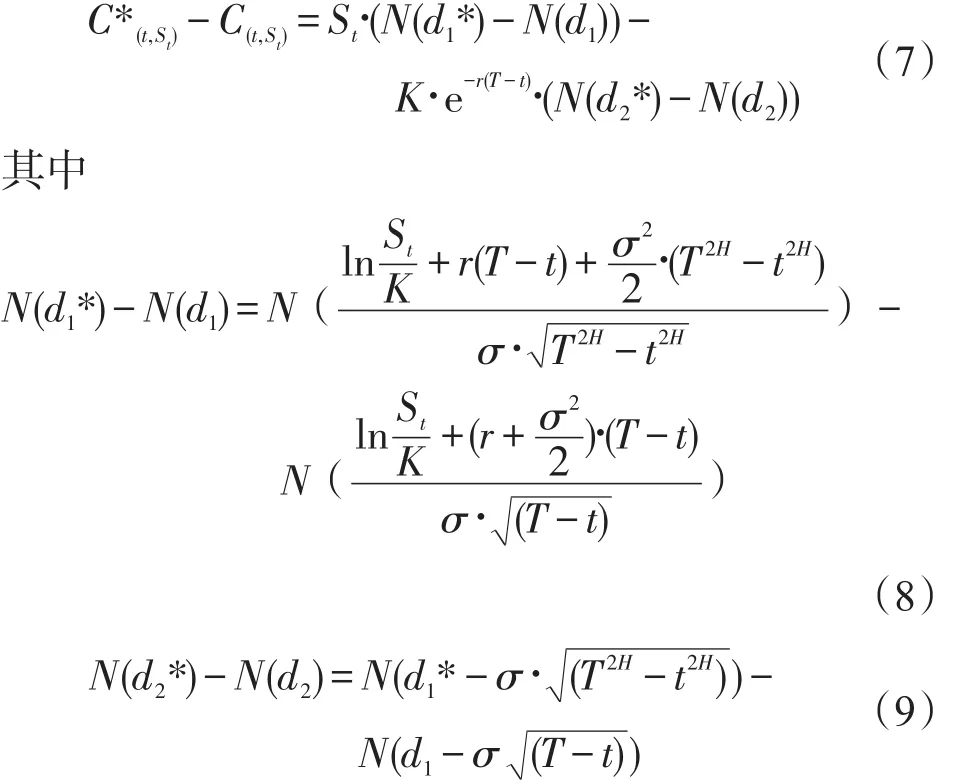
式（7）中，St和K∙e-r(T-t)均为正值，因此H指数的引入对实物期权价值的影响决定于式（8）和式（9）的结果符号.

为了检验H指数的引入对实物期权价值的影响，以下对式（8）和式（9）的差值结果进行求解计算.

当 H＞0.5时，由于通常取 0＜T＜1，则T2H-t2H＜T-t，可知，一般情况下会有，即d1*＞d1,进而有N(d1*)＜N(d1).同时可知，即d2*＞d2，进而有N(d2*)＞N(d2).

由此可知一般情况下会有C*(t,St)-C(t,St)=St∙(N(d1*)-N(d1))-K∙e-r(T-t)∙(N(d2*)-N(d2))＜0，即H＞0.5时，分形期权计算出的投资的风险价值小于传统B-S模型计算出的实物期权价值[16].因此以B-S定价模型计算船舶投资的期权价值会高估投资之后的选择权价值，从而容易使投资者对船舶投资产生盲目乐观心理，导致决策失误.

3.3 案例分析

A企业为国内某大型船公司，为扩大规模，A企业计划投资20 000万美元用于开发远东-澳洲航线，计划开发期限20年.专家根据近年来的航运业发展情况，预计投资该航线后，若收益好，前5年内每年可获得7 000万美元，则5年后可选择追加投资；若收益不好，前5年每年只能获得4 000万美元，则5年后选择收缩甚至放弃投资，即投资该航线使A企业获得了包括扩张期权、收缩期权、放弃期权等在内的多种期权.表3为开发期限内该航线净现金流量情况.

表3 20年内航线净现金流量表（万美元）Table 3 Net cash flow in 20 years of this route(million dollars)

由于在经济形势不好时，实物期权的价值对A企业来说显得更加重要，因此本案例分别以分形期权定价模型和传统B-S定价模型计算当收益不好时A企业选择权的价值，从而更加直观地说明传统B-S定价模型高估船舶投资的风险价值.

在式（1）–式（6）中，各参数的取值分别为：r= 12%，σ=50%[15]，T=0.4，t=0，S(t)=20 000万美元，万美元.

（1）传统B-S期权价值计算结果.

由式（1）计算得传统B-S定价模型期权价值为

C(t,St)=St∙N(d1)-K∙e-r(T-t)∙N(d2)=6 569（万美元）.

（2）分形期权价值计算.

由式（5）计算得分形期权价值为

C*(t,St)=St∙N(d1*)-K∙e-r(T-t)∙N(d2*)=6 374（万美元）.

（3）结果对比说明.

由以上两种计算结果可看出，在该案例背景下，传统B-S定价模型计算出的船舶投资期权价值C(t,St)为6 569万美元，而依据分形期权理论计算出的船舶投资的风险价值C*(t,St)为6 374万美元，小于6 569万美元.

因此可看出，以加入了H指数的分形期权定价公式计算出的船舶投资的风险价值较低，说明传统B-S定价模型高估了管理柔性在投资中的价值.

4 研究结论

针对目前实物期权定价模型中与实际不符的正态分布假设，本文以分形分布代替正态分布，建立了分形期权定价模型.并利用1999–01至2013–08的BDI对数收益率数据进行实证分析，结果表明BDI收益率序列的H指数为0.745，大于0.5，具有明显的尖峰厚尾特征.而在H＞0.5时，以B-S定价模型计算出的实物期权价值大于分形期权价值，即高估了船舶投资后的选择权价值.

需要注意的是，实物期权价值本质上是一种管理柔性价值，即投资发生后，航运企业根据经营效益变化及时调整投资策略所能得到的价值.但与金融资产不同，船舶作为重资产，一般不可随时变现.尤其是在国际贸易行情下滑时，能否找到接手人往往会成为重要难题，这也是实物期权问题的研究方向之一，由于篇幅所限本文不能一一涉及.但是，将分形思想引入到船舶实物期权价值计算中，从而更准确反映船舶投资的风险价值仍然具有较大意义.

[1]Cheng P C.Financial management in the shipping industry[M].Maryland:Cornell Maritime Press,1979.

[2]Frankel E G.Management and operations of american shipping[M].Auburn House Publishing Company,1982.

[3]Myers S.Determinants of corporate borrowing[J].Journal of Financial Economies,1977(5):147-175.

[4]阿维纳什·迪克希特，罗伯特·平迪克.不确定条件下的投资[M].中国人民大学出版社,2002. [Avinash K Dixit,Robert S Pindyck.Investment under uncertainty[M].China Renmin University Press Co.,LTD, 2002.]

[5]蒋义青.实物期权方法在船舶投资决策中的应用研究[D].上海:上海海运学院，2002.[JIANG Y Q.A study on the application of real option method in the decision making of shipping investment[D].Shanghai:Shanghai Maritime University,2002.]

[6]邵瑞庆.国际航运投资决策研究综述[J].交通运输工程学报，2003,3(4):116-120.[SHAO R Q.Review on decision making for international shipping investment[J].Journal of Traffic and Transportation Engineering,2003,3(4):116-120.]

[7]Helen B Bendall,Alanf Stent.Ship investment under uncertainty:Valuing a real option on the maximum of several strategies[J].Maritime Economies&Logistics，2005(07):19-35.

[8]李耀鼎.不确定条件下的船舶投资决策研究[D].上海:上海海事大学，2007.[LI Y D.Ship investment under uncertainty[D].Shanghai:Shanghai Maritime University,2007.]

[9]杨林达.基于复合实物期权理论的船舶投资决策理论与方法研究[D].大连:大连海事大学，2009.[YANG L D.Research of ship investment decision theory and method based on compound options theory[D].Dalian: Dalian Maritime University,2009.]

[10]蒋林,赵旭.实物期权方法在船舶投资决策中的应用[J].中国水运，2008,8(2):185-187.[JIANG L, ZHAO X.The application of real option method in the decision making of shipping investment[J].China Water Transport,2008,8(2):185-187.]

[11]李耀鼎,宗蓓华.国际干散货运价波动与随机游走检验[J].大连海事大学学报,2006,32(4):5-10.[LI Y D,ZONG B H.Fluctuations in the international dry bulk freight and random walk test[J].Journal of Dalian Maritime University,2006,32(4):5-10.][12]翟海杰、李序颖.不同分布的GARCH族模型的波罗的海干散货运价指数波动率[J].上海海事大学学报, 2009,30(3):59-64.[ZHAI H J,LI X Y.Volatility of Baltic dry index using GARCH type model swith different distributions[J].Journal of Shanghai Maritime University,2009,30(3):59-64.]

[13]万九文,吕靖，魏方，等.国际干散货运输市场分形特征[J].大连海事大学学报,2010,36(3):31-34.[WAN J W，LV J,WEI F,et al.Fractal characteristics of international dry shipping industry[J].Journal of Dalian Maritime University,2010,36(3):31-34.]

[14]李电生、万培祥.干散货航运价格指数分形结构研究[J].北京交通大学学报(社会科学版),2012,11 (3):51-56.[LI D S,WAN P X.A fractal structure study on shipping price index of dry bulk[J].Journal of Beijing Jiaotong University(Social Sciences Edition), 2012,11(3):51-56.]

[15]唐友刚,于巧婵,罗延生,等.基于实物期权的航运企业船舶投资决策研究[J].内蒙古工业大学学报(社会科学版),2011,20(1):34-38.[TANG Y G,YU Q C, LUO Y S,et al.Shipping investment decision based on real options[J].Journal of Inner Mongolia University of Technology(Social Sciences Edition),2011,20(1):34-38.]

[16]黄怡蓉.中国股市分形结构的理论研究与实证分析[D].厦门:厦门大学.2004.[HUANG Y R.A study on fractal structure in Chinese stock market—theoretical&empirical discussion[D].Xiamen:Xiamen University,2004.]

Empirical Study on Ships Investment Decisions Based on Fractal Option Theory

LI Dian-sheng,ZHANG Sheng-ze
（School of Economics,Ocean University of China，Qingdao 266100,Shandong,China）

As the most important means of production,the early investment decision analysis of ships is vital to shipping company.All along,the calculated of investment risk value of the ship is one problem plagued to people.The development of real options theory and B-S pricing model provide a solution,but the most important assumption of B-S pricing model is that asset price volatility in line with the normal distribution which has a large gap between realities.The fractal option pricing model is established,and the fractal distribution assumption is chose in lieu of the normal assumption in B-S pricing model.Then the BDI index is used as empirical analysis.The result shows that H index of BDI logarithm yield sequence is greater than 0.5.On this condition,the ship investment real option value based on traditional B-S pricing model is greater than the fractal options value.This proves that B-S pricing model overestimate the real risk value of ship investment.Finally investors are prone to have psychological of blind optimism and increasing investment risk.

waterway transport;ships investment decisions;fractal option;B-S pricing model;BDI

1009-6744（2015）01-0037-06

：F253.9

：A

2014-07-28

：2014-12-08录用日期：2014-12-15

教育部人文社科基地项目（2014JDZS03）.

李电生（1966-），男，河北石家庄人，副教授. ＊

：zhangshengze1234@126.com