基于等价舵角的可回转双桨推进船舶操纵研究*

魏宏磊 褚建新 黄 辉

(上海海事大学航运技术与控制工程交通部重点实验室 上海 201306)

基于等价舵角的可回转双桨推进船舶操纵研究*

魏宏磊 褚建新 黄 辉

(上海海事大学航运技术与控制工程交通部重点实验室 上海 201306)

舵角大小是影响船舶操纵性指数的重要因素之一.为研究可回转双桨的控制规律，建立了单桨单舵船舶和可回转双桨电力推进船舶两者之间的联系，可推得与可回转双桨电力推进船舶能产生相同舵效的单桨单舵船舶的舵角，即等价舵角.并按螺旋桨的工作状态将船舶操纵分为3大类.为这类船舶的设计与操纵控制提供依据.

可回转双桨；等价舵角；相似性原理；操纵控制

对于尾轴推进的双桨双舵型船舶，其运动模型可从单桨单舵船舶运动模型扩展而来[1].文献[2-4]对双桨双舵船舶的操纵特性进行研究.内容包括双桨双舵船舶的数学模型，单桨单舵船舶与双桨双舵船舶操纵性能比较，转舵速度对船舶操纵的影响，离靠泊操作时的操纵研究等.现有文献多针对单桨单舵船舶和双桨双舵船舶进行操纵特性研究，鲜有文献对无舵可回转双桨推进方式进行研究.文献[5]采用智能方法建立了可回转桨的水动力模型，并研究了可回转桨的操纵性能.但考虑有所欠缺，并未考虑到螺旋桨回转的方向性，且没有建立可回转双桨推进操纵与单桨单舵船舶和双桨双舵船舶操纵之间的量化关系.

在可回转双桨作用下，船舶的推进运动与转船运动高度耦合，双桨的回转作用产生舵效.本文研究可回转双桨回转角控制与单桨单舵操纵舵角的关系，研究表明，可回转双桨在同回转同转速工况下船舶操纵性能最佳.

1 常规尾舵水动力分析

1.1 常规尾舵流体动力特性

采用常规尾舵进行船舶航向保持和改变主要依靠水流对舵叶产生的作用力.如当船舶偏离航向时，转动舵叶，产生作用于船舶的转船力矩，使船舶返回到正航向.而当采用无舵全回转双桨推进方式时，则需要通过双桨的回转和双桨的转速差来实现船舶的航向控制.

图1所示为常规尾舵航行时作用力分析.

U-水流方向的流速；α-冲角；D-沿流速方向的阻力；L-垂直于流速方向的升力；FR-舵上产生的流体动力；Fδ-舵叶面的正压力；FT-沿舵叶面的切向力.图1 常规尾舵作用力分析

由图1可得到如下关系式[6].

(1)

在敞水中，舵叶面的正压力Fδ可以用下式计算：

(2)

式中：AR为舵叶的面积；U为舵叶来流速度；fα为升力系数CL在冲角α=0°时的斜率，是舵展弦比λ的函数，可由藤井公式计算；α为冲角(敞水中，冲角等同于舵角，即α=δ).

1.2 常规尾舵动力学模型

不考虑船舶横摇运动的影响，将Fδ分解为在纵荡X、横荡Y、和首摇N上的分量XR，YR，NR：

(3)

式中：δ为舵角；tR为舵力的减额系数；d1R和d2R为舵作为船舶的附体对横漂力和回转力矩的影响系数，可由实验给出；xG为船舶重心G到2舵柱之间连线的水平距离.

2 可回转双桨推进特性

2.1 螺旋桨位置

图2为可回转双螺旋桨在船舶上布局图所示，下标(P)和(S)分别表示左、右舷推进螺旋桨.船舶左、右舷可回转螺旋桨的回转柱距离过船舶重心G的船舶首尾线长度为x(P)和x(S).距船舶首尾线距离分别为y(P)和y(S)，这里将x(P)/y(P)=K(P)和x(S)/y(S)=K(S)定义为尺度系数.在螺旋桨位置完全对称情况下，x(P)=x(S)=xG，y(P)=y(S)=yG.

图2 可回转双螺旋桨在船舶上布局图

2.2 螺旋桨推力特性

设螺旋桨盘面直径为D，左右螺旋桨形成推进力的转速分别为n(P)和n(S)，对于电力推进船舶，通过推进电机调节转速，则左右螺旋桨在敞水中产生在轴向方向上的推力表示为

(4)

式中：ρ为水密度；kT(P)和kT(S)分别为左右舷螺旋桨的推力系数，是进速系数J的函数，可由经验公式给出[7].

图3 螺旋桨推力和回转角

2.3 桨推力分解

设左右舷螺旋桨水平回转角分别为φ(P)和φ(S)(顺时针方向为正方向)，双桨结构相同，对称安装在船尾.根据图3的几何关系，可得左右螺旋桨推进力在船舶运动坐标系X，Y，N方向上的投影分量分别为

(5)

(6)

假定螺旋桨的推力减额系数t(P)=t(S)=tP，横漂力影响系数d1(S)=d1(P)=d1P，转船力矩影响系数d2(S)=d2(P)=d2P，则敞水时螺旋桨的流体动力模型可表示为

(7)

船舶在左右桨推力T(P)和T(S)作用下，在运动坐标系x方向的常规推力减额tP；由于左右桨回转，推力在y方向上产生的分力T(P)sinφ(P)和T(S)sinφ(S)造成船舶横漂运动.由于左右双桨的回转和推力而产生舵效，即使螺旋桨不做回转(概念上的不动舵)φ(P)=φ(S)=0(即可以视为尾轴固定无回转双桨推进方式)，当左右舷螺旋桨转速不同时n(P)≠n(S)也会产生实际舵效，使船舶航向发生改变，当左右舷螺旋桨转速相同n(P)=n(S)时，保持船舶航向不改变.

2.4 回转角为零时的特例

φ(P)=φ(S)=0时式(7)可退化为艉轴固定无回转双桨推进的动力模型：

(8)

式(8)由于螺旋桨不可回转，因此不产生船舶的横漂力.但是当2个螺旋桨转速不同时，产生的推力不同，2螺旋桨推力产生的转船力矩方向彼此相反.当T(P)>T(S)船舶有向右旋转的转船力矩，NP<0；T(P)0.

3 等价舵角推导

3.1 推导过程

将左、右舷双侧螺旋桨的推力T分解在X，Y和N上的分量(与推进器安装位置和船舶几何尺寸有关)，根据相似性原理，可得到双桨推进船舶的等价舵角.

因螺旋桨回转角度及方向不同产生的转船力矩大小及方向不同.在获得与常规舵相同的舵力和转矩情况下，将式(3)和式(7)联立，得：

(9)

结合式(2)，(3)和(7)中第三式和式(9)中第三式可推得：

(10)

为了便于阐述，这里考虑正车时螺旋桨特性，因此可将式(4)转化为

(11)

将其代入式(10)中得到：

(12)

设α=δ，则式(12)可化简为

(13)

式中：

3.2 等价舵角计算

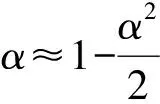
(14)

对可回转双桨电力推进船舶可按螺旋桨工况对等价舵角计算模型分类化简，按螺旋桨工况主要可分为3类：(1)左右舷螺旋桨同回转且转速相等；(2)单桨回转双桨相同转速；(3)单桨回转，转动.下面是等价舵角计算模型的分类化简结果.

3.3 左右舷螺旋桨同回转且转速相等

3.4 单桨回转双桨相同转速

仅左桨回转，双桨转速相同，即：φ(S)=0,φ(P)≠0，n(P)=n(S)=nP时，i(S)=i(P)=iP.得到等价舵角-回转角关系式为

仅右桨回转，双桨转速相同，即：φ(S)≠0,φ(P)=0，n(P)=n(S)=nP时，i(S)=i(P)=iP.得到等价舵角-回转角关系式为

3.5 单桨回转且转速不为零

仅左桨回转，转速不为零，即φ(S)=0,n(S)=0，φ(P)≠0，n(P)=nP时，得到等价舵角-回转角关系式为

仅右桨回转，转速不为零，即φ(P)=0,n(P)=0，φ(S)≠0，n(S)=nP时，得到等价舵角-回转角关系式为

4 仿真实验

参考船型：216客位电力推进客渡轮，船长36.00 m，型宽8.40 m， 型深1.90 m，吃水1.10 m，排水量120 t，额定航速10 kn.电力推进仿真参数：双机双桨可回转推进系统，螺旋桨为4叶定桨距，盘面直径0.90 m，额定转速500 r/min，双桨立柱间距5.60 m，重心距螺旋桨回转立柱距离为15.2 m.推进电动机的额定功率2×90 kW[1].

对于参考船型通过数值仿真可得到不同工况下等价舵角与回转角的关系.

4.1 左右舷螺旋桨同回转且转速相等

如果左右舷双桨回转角φ(P)=φ(S)=0，无论产生多大推力都不能产生转船力矩；而当螺旋桨转速为零n(P)=n(S)=0，无论回转角多大同样无法产生转船力矩.只有在转速和回转角都不为零时产生转船力矩.参见3.3中推出的函数关系.图4所示为双桨同回转，同转速时回转角-等价舵角的关系.

图4 双桨同回转，同转速时回转角-等价舵角关系

4.2 单桨回转双桨相同转速

在这种工况下，可分2种操纵情形.第一种操纵情形，左桨回转角φ(P)≠0，左右舷螺旋桨转速n(P)=n(S)≠0；第二种操纵情形，右桨φ(S)≠0，左右舷螺旋桨转速n(P)=n(S)≠0(参见3.4函数关系).图5所示为左桨回转，双桨同转速时回转角-等价舵角的关系.图6所示为右桨回转，同转速时回转角-等价舵角的关系图.

图5 左桨回转，双桨同转速时回转角-等价舵角关系

图6 右桨回转，双桨同回转时回转角-等价舵角关系

4.3 单桨回转且转速不为零

这种工况下，可分2种操纵情形.第一种操纵情形，左桨回转角φ(P)≠0，左桨转速n(P)≠0；第二种操纵情形，右桨φ(S)≠0，右桨转速n(S)≠0(参见3.5函数关系).图7所示为左桨回转，双桨同转速时回转角-等价舵角的关系.图8所示为右桨回转，同转速时回转角-等价舵角的关系图.

图7 仅左桨回转，转动时回转角-等价舵角关系

图8 仅右桨回转，转动时回转角-等价舵角关系

比较图4～图8可知，在相同回转角变化时，双桨同回转操纵方式比其他方式操纵时的等价舵角范围大，即具有良好的操纵性.其等价舵角与回转角成正比例关系.

在单桨操纵时，左桨回转，且转速不为零时，具有较偏大的负舵角(左舵)，而右桨回转，且右桨转速不为零时，具有相对偏大的正舵角(右舵).

在单桨回转操纵时，左桨回转且转动和右桨回转双桨同转速均便于操左舵；而右桨回转单桨且转动和左桨回转双桨同转速均便于操右舵.

由于舵角是影响舵效的主要因素之一，一定范围内，舵角越大舵效越好.总的来说，左桨回转操纵比右桨回转操纵的操左舵效果好，而右桨回转操纵比左桨回转操纵的右舵效果好；两个螺旋桨回转角的总角度相同时，单桨比双桨具有等价舵角大；回转角角度相同时，双桨可得到比单桨更大的等价舵角.

5 结 束 语

有尾舵船的舵角和航速是影响舵效的重要因素，而在无舵的可回转船，回转角与转速则是影响舵效的重要因素.本文分别通过单桨单舵船舶和可回转双桨推进船舶力学分析，依据相似性原理，建立了舵操纵和可回转桨操纵之间联系，并建立参考船型在双桨不同推力给定、不同回转角给定工况下可回转双桨推进船舶的等价舵角计算模型.讨论了不同工况下可回转双桨等价舵角与回转角之间的关系，可为这类船舶的操纵控制提供理论依据.

[1]康 伟，褚建新.可回转双桨电力推进船舶运动模型的研究[J].中国造船,2012,53(1):107-116.

[2]LEE S K, FUJINO M. Assessment of a mathematical model for the manoeuvring motion of a twin-propeller twin-rudder ship[J].International Shipbuilding Progress， 2003,50(1/2):109-123.

[3]王化明，邹早建.双桨双舵船舶操纵性预报研究[J].武汉理工大学学报：交通科学与工程版，2006,30(1)：124-127．

[4]刘 伟，许 晟,王永宁，等.转舵速度对船舶操纵性影响研究[J].中国水运，2014,14(2):1-3.

[5]刘百顺，徐玉如.可回转桨的水动力模型与操纵性能[J].海洋工程，1999,17(1):27-33.

[6]贾欣乐，杨盐生.船舶运动数学模型:机理建模与辩识建模[M].大连:大连海事大学出版社,1999.

[7]范尚雍.船舶操纵性[M].北京:国防工业出版社,1988.

Study on the Propulsion of the Rotatable Twin-propeller Propulsion Ship based Equivalent Rudder Angle

WEI Honglei CHU Jianxin HUANG Hui

(KeyLaboratoryofMarineTechnologyandControlEngineeringofMinistryofCommunication,ShanghaiMaritimeUniversity,Shanghai201306,China)

The rudder angle is one of the important factors that affect the maneuverability. In order to study the control law of the rotatable twin-propeller, the relationship between the one propeller-one rudder ship and the rotary paddles electric ship is set up. The equivalent rudder angle, which represented the angle of the one propeller-one rudder ship that generate the same effect as the rotary twin-propeller propulsion ship did. On basis of the different propeller working conditions, the control mode of the twin-propeller propulsion ship could be divided into three types, which provided the knowledge the design and the maneuverability for the ship of this kind.

the two rotatable paddles; the equivalent rudder angle; rotation angle; the maneuverability

2014-12-10

*交通部应用基础研究项目资助(批准号：2013329810350)

U664

10.3963/j.issn.2095-3844.2015.03.035

魏宏磊(1986- )：男，博士生，主要研领域为船舶电力推进故障诊断