非饱和重塑黄土土-水特征曲线与渗透系数模型预测

张培印，李顺群

(天津城建大学 土木工程学院，天津 300384)

非饱和重塑黄土土-水特征曲线与渗透系数模型预测

张培印，李顺群

(天津城建大学 土木工程学院，天津 300384)

在分析土-水特征曲线及预测非饱和土渗透系数方法的基础上，以甘肃兰州重塑黄土为研究对象，采用非饱和土固结仪，测定初始饱和度相同、干密度不同的土样的土-水特征曲线，基于拟合效果较好的Fredlund & Xing三参数方程对试验数据进行拟合．以实测的土-水特征曲线为基础，采用 Childs & Collis-Geroge 预测非饱和渗透系数的模型，计算得到非饱和黄土渗透系数与基质吸力的关系，结果表明：渗透系数随吸力的增大呈非线性减小，两者的关系可用幂函数表示，这为黄土地区土体工程性质的研究和预测，如降雨入渗的边坡稳定性评价、非饱和地基湿陷变形计算等提供了理论支持．

非饱和土；土-水特征曲线；渗透系数；模型预测

非饱和土的分布十分广泛，土坝、铁路和公路路基填土等与实际工程密切相关的地表土均处于非饱和状态[1]．非饱和土不同于饱和土的根本原因就是其基质吸力的存在，非饱和土的基质吸力随着含水量的变化而变化，含水量与基质吸力的关系称为土-水特征曲线．非饱和土土力学的发展是围绕吸力这一基本概念展开的．在非饱和土的许多研究领域，如强度理论、固结理论、本构理论等都涉及到土-水特征曲线的应用．

另外，土-水特征曲线还可以用来预测非饱和土体的渗透系数[2-4]．渗透系数是非饱和土的重要参数之一，它的取值直接影响到渗流的计算．国内学者通过室内试验对非饱和土的渗透系数进行了研究：高永宝等[5]利用水-气运动联合测试仪，对一定湿密状态下的黄土做了大量的渗透系数测量试验；王铁行等[6]采用水平土柱入渗法，测量了不同干密度压实黄土的水分扩散率与体积含水率的关系，分析了黄土渗透系数随干密度和含水率的变化规律；徐永福等[7]通过常水头稳态试验测量非饱和土的渗透系数，并且分析了压应力对渗透系数的影响；赵彦旭等[8]采用非饱和导水率测定系统进行非饱和渗透系数测量，得到不同干密度压实黄土的渗透系数与吸力的关系．

然而，通过室内试验进行的测量不仅操作复杂、耗时耗力，而且现有仪器的可操作性仍有待于提高，同时测量精度也尚未得到验证．因此，国内外不少学者致力于由土-水特征曲线来预测非饱和土的渗透性函数[9-10]，从而得到渗透系数与基质吸力之间的关系．

以甘肃兰州黄土为研究对象，通过非饱和土固结仪测得其土-水特征曲线，再采用常见的理论模型对试验数据进行拟合；然后，以实测的土-水特征曲线为基础，采用Childs & Collis-Geroge预测非饱和渗透系数的模型，计算得到非饱和黄土渗透系数与基质吸力之间的关系．

1 土-水特征曲线试验

试验所用土样取自甘肃兰州五泉山，成分主要是以细颗粒土为主，颗粒组成为：粒径＜0.005,mm的占9.3%；0.005,mm＜粒径＜0.075,mm的占65.3%；0.075,mm＜粒径＜2,mm的占25.4%．土体的物理性质指标如表1所示．

表1 土体的基本物理性质指标

1.1 重塑土样的制备

将取回的土样风干碾碎，过2,mm筛，测量土样的风干含水率，并计算制备一定含水率和干密度的土样所需的加水量，将拌好的土样密封保存24,h，使含水率均匀．采用击实法制作出土饼，然后用环刀直接切取出试验土样，通过质量控制干密度分别为1.70、1.60、1.50,g/cm3，其基本性质指标见表2．在饱和土中，渗透系数是孔隙比的函数，但是在分析问题时，一般假定饱和土的渗透系数为常数，这里假定为5× 10-6,m/s．

表2 试样的基本性质指标

1.2 土-水特征试验研究

采用非饱和土固结仪测量非饱和重塑黄土干燥过程中的土-水特征曲线．三组土样初始饱和度均接近1.0，可以认为已经饱和．试验时，以20，50，100，200，400,kPa逐级施加气压．非饱和土固结没有固定的稳定标准，该次试验以排出水体积10,mm3/h为稳定标准，每一级气压力作用下，稳定时间在2,d左右．试验测得的土-水特征曲线如图1所示．

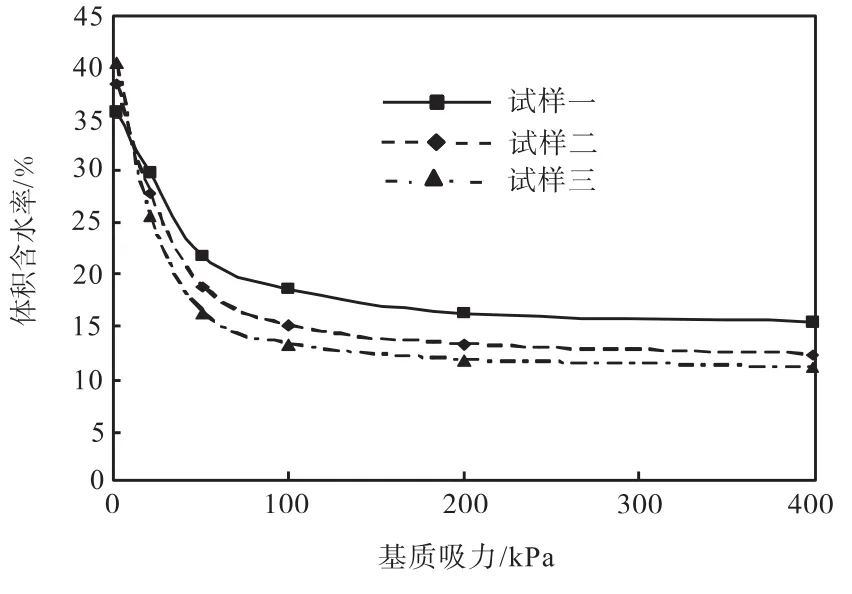
图1 试样的土-水特征曲线

由图1可以看出：基质吸力超过100,kPa后，含水率变化很小；换言之，需要很大的吸力才能使土体脱水．故将100,kPa吸力下对应的含水率作为残余含水率，三组试样的残余含水率分别为18.5%、15.0%、13.2%．

1.3 土-水特征曲线方程拟合

Fredlund & Xing三参数方程为

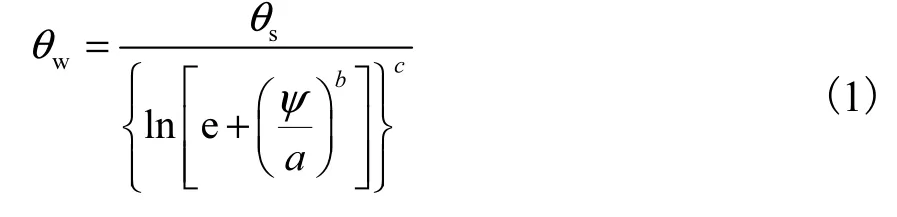
式中

θw—体积含水量；

θs—饱和体积含水量；

a—与进气值有关的参数，kPa；

b—在基质吸力大于进气值之后与土体脱水速率有关的土参数；

c—与残余含水率有关的试验参数；

ψ—基质吸力．

采用上述理论模型，分别对试验数据进行拟合．试验所得曲线以及三条拟合曲线如图2所示．由图2可以看出，Fredlund & Xing三参数方程拟合效果较好．各方程的参数拟合值见表3．

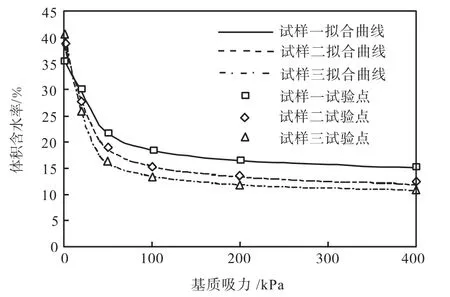
图2 三组试样土-水特征拟合曲线

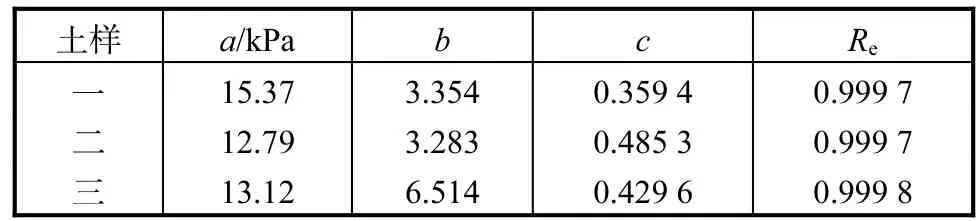
表3 参数拟合值

2 非饱和土渗透系数预测

许多学者提出了预测非饱和土渗透性的函数，一种是土-水特征曲线试验测量结果拟合经验公式；另一种是统计模型方法[11]．这些函数利用了饱和土渗透系数和土-水特征曲线．非饱和土渗透系数k不是一个常数，是基质吸力的函数，可根据饱和土渗透系数ks表示，相对渗透系数为

式中

k(θ)—随吸力变化的非饱和土渗透系数；

kr(θ)—相对渗透系数；

ks—饱和土体渗透系数．

由室内试验确定出土-水特征曲线后，把曲线沿体积含水率轴等分为m份，用每一等分中点的基质吸力根据下式计算渗透系数k(θ)i

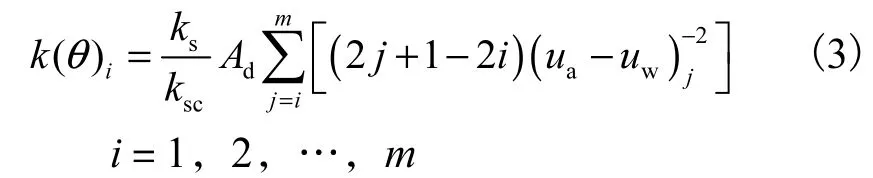
式中

k(θ)i—对应于第i等分中点的体积含水率(θ)i的渗透系数，m/s；

ks—实测饱和渗透系数，m/s；

ksc—计算的饱和渗透系数，m/s；

Ad—调整常数，(m/s)·kPa2；

i—间断编号；

j—从i到m的计数．

m—试验土-水特征曲线上饱和体积含水率与最小体积含水率之间的等分数；

(ua－uw)j—相应于第j个间段中点的基质吸力值．

式中

Ts—水的表面张力，kN/m，取7.28×10-5kN/m；

ρw—水的密度，kg/m3；

g—重力加速度，m/s2；

μw—水的绝对黏度，N·s/m2，取100.5× 10-5,N·s/m2；

θs—饱和体积含水率；

p—计及不同尺寸孔隙的相互作用的常数，可假设为2.0；

N—饱和体积含水率与零体积含水率之间的计算间断总数，N＝m[θs/(θs－θL)]；

θL—相应于试验土-水特征曲线上的最小体积含水率，m≤N．

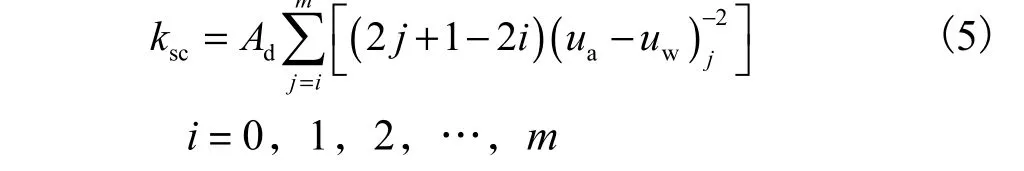
式中

(ua－uw)j—相应于第j个间段中点的基质吸力值．

以试样一为对象进行预测，对试验所得土-水特征曲线取m＝20，计算得N＝35，Ad＝2.743×10-5,(m/s)·kPa2，ksc＝4.361×10-5,m/s．预测的非饱和土渗透系数曲线见图3．

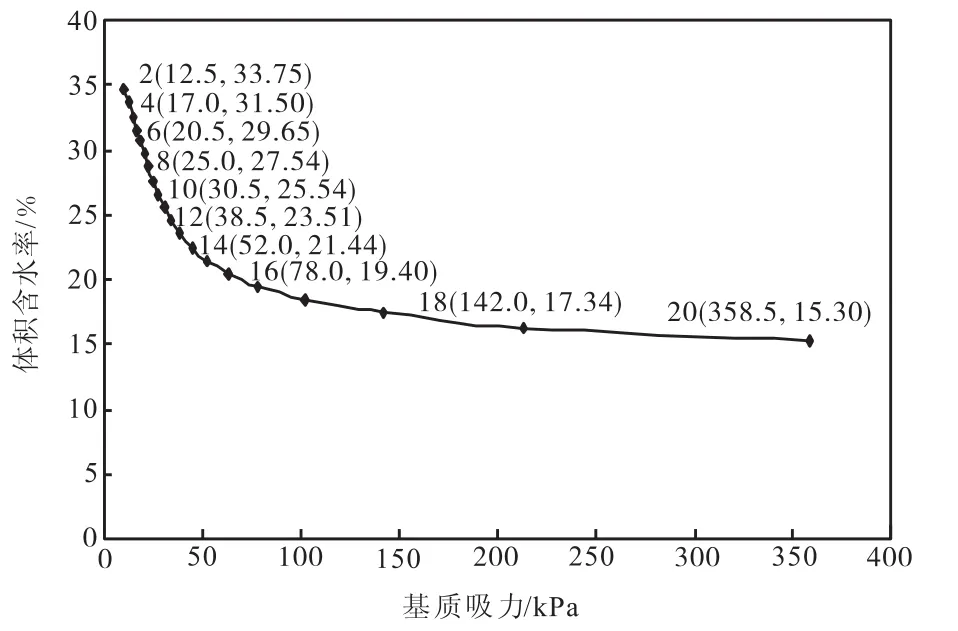
图3 预测非饱和土渗透系数曲线

由图3可知，使土样每降低相同体积含水率，需要增加的基质吸力逐步增大．从图3曲线上求出各间断中点对应的基质吸力值，然后计算出渗透系数，见表4．

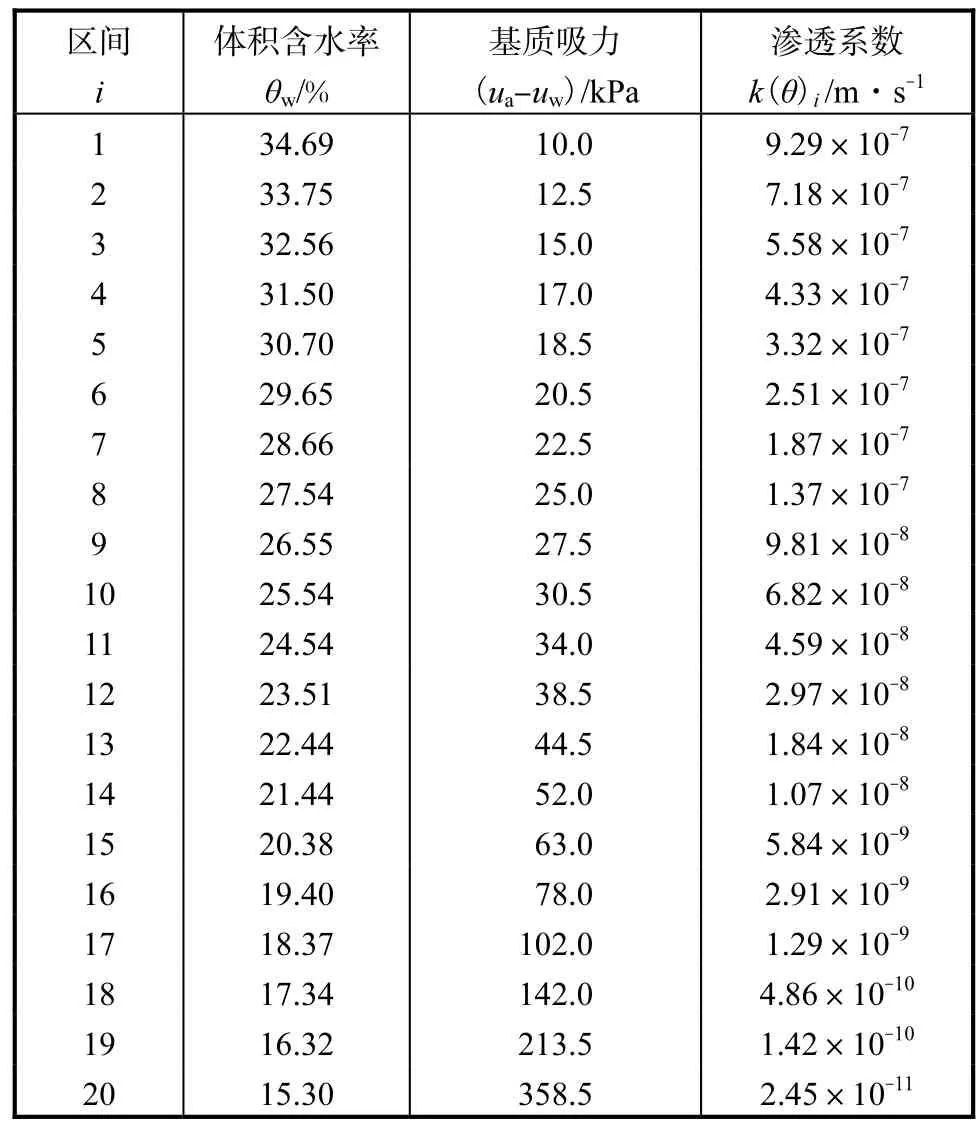
表4 不同吸力对应的含水量以及渗透系数

对于三组试样，基质吸力与渗透系数的关系曲线见图4．通过对曲线拟合分析，发现非饱和渗透系数与基质吸力的关系可用幂函数表示．

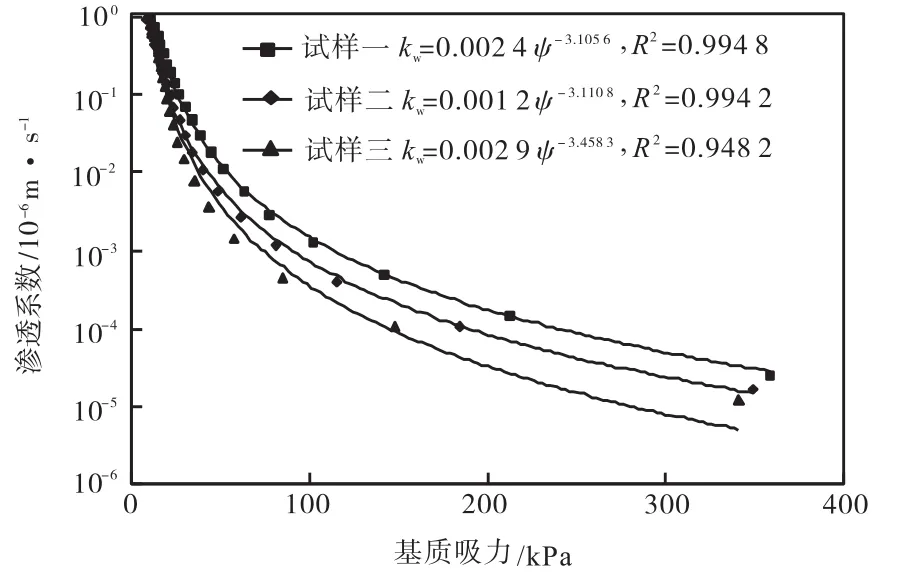
图4 渗透系数与基质吸力的关系曲线

由图4可以看出：所研究的非饱和黄土的渗透系数随基质吸力的增大而迅速减小，呈现出强非线性．

3 结 论,

(1)随着吸力的增大，体积含水率迅速降低，吸力大于100,kPa后，体积含水率变化很小，达到了残余含水率．

(2)采用Fredlund & Xing三参数模型对实测数据进行拟合，效果良好．

(3)采用间接法预测非饱和土的渗透系数随基质吸力的变化规律，随着脱水过程的继续，渗透系数迅速减小，之后曲线趋于平稳，呈现出强非线性，两者之间的关系可用幂函数表示．

［1］ FREDLUND D G，RAHARDJO H. 非饱和土土力学[M]. 陈仲颐，张在明，陈愈炯，等，译. 北京：中国建筑工业出版社，1997.

［2］ Van GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal，1980，44(5)：892-898.

［3］ FREDLUND D G，XING A，HUANG S. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve[J]. Canadian Geotechnical Journal，1994，31(3)：533-546.

［4］ 卢应发，陈高峰，罗先启，等. 土-水特征曲线及其相关性研究[J]. 岩土力学，2008，29(9)：2,481-2,486.

［5］ 高永宝，刘奉银，李 宁. 确定非饱和土渗透特性的一种新方法[J]. 岩石力学与工程学报，1999，20(3)：1-6.

［6］ 王铁行，卢 靖，张建锋. 考虑干密度影响的人工压实非饱和黄土渗透系数的试验研究[J]. 岩石力学与工程学报，2006，25(11)：2,364-2,368.

［7］ 徐永福，兰守奇，孙德安，等. 一种能测量应力状态对非饱土渗透系数影响的新型试验装置[J]. 岩石力学与工程学报，2005，24(1)：160-164.

［8］ 赵彦旭，张虎元，吕擎峰. 压实黄土非饱和渗透系数试验研究[J]. 岩土力学，2010，31(6)：1,809-1,812.

［9］ 刘晓东，施建勇. 基于土水特征曲线预测城市固体废弃物(MSW)非饱和渗透系数研究[J]. 岩土工程学报，2012，34(5)：855-862.

［10］ 胡 冉，陈益峰，周创兵. 考虑变形效应的非饱和土相对渗透系数模型[J]. 岩石力学与工程学报，2013，32(6)：1,279-1,287.

［11］ LU Ning，LIKOS W J . 非饱和土力学[M]. 韦昌富，侯 龙，简文星，译. 北京：高等教育出版社，2012，359-360.

The Prediction Model Research of Soil-water Characteristic Curve and Permeability Coefficient of Unsaturated Remolded Loess

ZHANG Pei-yin，LI Shun-qun
(School of Civil Engineering，Tianjin Chengjian University，Tianjin 300384，China)

Based on the analysis of soil water characteristic curve and prediction method of permeability coefficient,this paper takes remolded loess in Lanzhou of Gansu province as research objects. Soil water characteristic curve is obtained from the unsaturated soil consolidation apparatus,and the experimental data are then fitted with Fredlund & Xing Equation which has a better fitting effect. With the use of permeability prediction on Childs & Collis-Geroge Model,the relationship between permeability coefficient and matrix suction is built on the strength of the measurement of soil-water characteristic curve. The results show that the permeability coefficient decreases along with the nonlinear increase of the matrix suction,and they can be expressed in power function. It provides theoretical support to the research and prediction of engineering properties in loess area,such as slope stability evaluation under rainfall infiltration and the calculation of collapsibility deformation for unsaturated foundation.

unsaturated soil；soil-water characteristic curve；permeability coefficient；prediction model

TU444

A

2095-719X(2015)02-084-05

2014-10-29；

2014-11-28

国家自然科学基金(51178290)

张培印（1990—），男，河南濮阳人，天津城建大学硕士生．

李顺群（1971—），男，教授，博士，从事非饱和土方面的研究．E-mail：lishunqun@sina.com