出平面剪切线源作用下沉积盆地地震响应谱元法模拟

韩建彬，刘中宪，罗兆辉

(天津城建大学 土木工程学院，天津 300384)

土木工程

出平面剪切线源作用下沉积盆地地震响应谱元法模拟

韩建彬，刘中宪，罗兆辉

(天津城建大学 土木工程学院，天津 300384)

由于盆地内外介质的阻抗差别及特殊的几何形状，盆地内部将出现显著的地震动放大效应．针对出平面线源作用下沉积盆地地震响应问题，利用谱元法研究了震源主频率、空间位置和沉积盆地形状等因素对沉积盆地地震响应的影响．数值分析表明：点源的频率和沉积形状对地表的响应影响较大；点源的不同位置对于边缘效应有一定影响．

沉积盆地；出平面剪切线源；谱元法；地震响应

国内外多次大地震震害调查表明，沉积盆地内部往往会出现烈度异常区域．这主要由于盆地内外介质的阻抗差别及其特殊的几何形状，使得波动能量容易进入，但很难再向外部逸散，地震波会在盆地边缘发生面波转换，并在内部某些区域产生聚焦效应，最终使得地震动幅值增大，持时变长，对高层建筑、大跨桥梁等自振周期较长的工程结构造成严重破坏[1]．如1985年墨西哥的8.1级地震，由于软土盆地效应，使得距震中400,km外的墨西哥城遭受严重破坏．我国也有许多大中城市位于沉积盆地之上，或者在城市中分布着古河道，或者曾经经历过大体积土体的开挖及回填．盆地效应的研究对于这些城市的防震减灾具有现实意义，同时也对认识盆地这种大型不均匀的场地条件对地震动的影响、促进地震工程学的发展具有重要意义．

目前，已有几种较为成熟的数值方法用于模拟地震波在沉积盆地中的传播和散射，包括有限元方法[2]、边界元法[3]、有限差分算法[4-5]、伪谱法以及谱元法[6-8]．

在上述方法当中，有限元法可以模拟各种复杂介质模型．该方法基于波动方程弱形式，能够自动满足自由边界条件，同时在解决非均匀复杂弹性介质模型时也很有优势[9]；然而有限元法需要比较强大的计算机资源，以及更多的计算时间，同时，低阶有限元法会出现令人不满意的频散现象[10]，而传统的高阶有限元法会产生虚假波．对于有限差分方法而言，在处理有规则的边界模型及介质速度或密度差别不是很大时的模型有优势[11-12]，但是很难有效处理自由界面和复杂的模型．在流体力学中的伪谱法已用于解决弹性动力学问题[13]，这种方法是用矩形网格到弯曲网格的映射算法来处理起伏的自由边界条件，因此需要大量的计算机资源．边界积分和边界元是另外两种可用于模拟自由起伏边界的数值方法，虽然这些方法计算效率高，但多限于线性均匀介质问题．另外需指出的是，上述研究大多假定为平面波入射，对于近场情况，可能会产生较大误差，因此宜采用点源(线源)解作为初步近似．

谱元法最早是由Patera[14]提出的，并用于流体力学中．该方法将有限元法和谱方法相结合，既有可以模拟任意复杂介质模型的优点，同时也保证了准确度．笔者针对出平面剪切线源作用下沉积盆地二维响应问题，采用谱元方法进行计算分析，讨论沉积盆地形状、不同震动频率、出平面剪切线源不同位置等因素对沉积盆地地震响应规律的影响．

1 计算模型

以出平面剪切线源为地震输入，研究任意形状二维沉积盆地的地震响应，如图1所示．采用谱元法，可方便地考虑地层剪切波速沿不同方向的变化．考虑土层的自重及密实度的影响，土体的密度及剪切模量随着埋深的增加逐渐增大，当垂直深度大于3,000,m时，假定为均质基岩半空间．

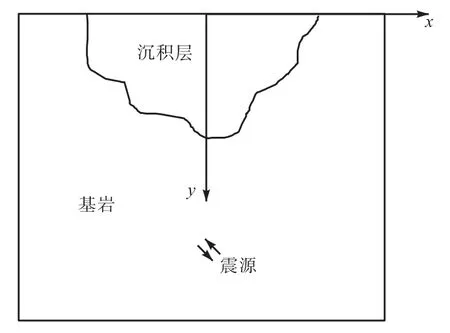
图1 计算模型

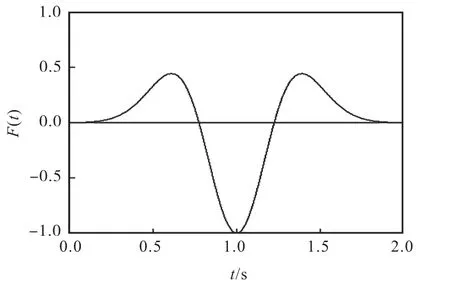
图2 震源激励函数曲线

2 计算方法

谱元法的基本思想是选取以正交多项式表示的基函数，基函数与Fourier级数中的正弦和余弦相类似，可以提高级数表示的解的收敛速度，其基本步骤是：①将计算区域分成许多子域(单元)；②在每个子域中将近似解表示成截断的Chebyshev或Lagrange正交多项式展开；③用Galerkin方法求解正交问题的变分格式，得到全局的近似解．谱元法是弹性波方程在空间近似的高阶变分方法，该方法能减少用于离散物理空间域的单元的数量，从而在很大程度上降低了计算成本[16]．

研究地震波在土体的传播，应该以半无限空间体为研究对象，但往往要取适当的有限区域来计算，所以边界问题就需要考虑设置人工吸收边界[17]．以二维有限空间域Ω∈R2为例，计算解决弹性波在不均一介质中传播问题．空间域Ω的边界为Γ，包括内部边界Γint和人工外部边界Γext．位移和速度分别用u(x,t)和v(x,t)来表示，包括计算域和边界，t∈I=[0,T ]，T为地震波的传播时间．

2.1 弹性波动谱元模拟的基本理论[18-19]

弹性波传播的运动方程为

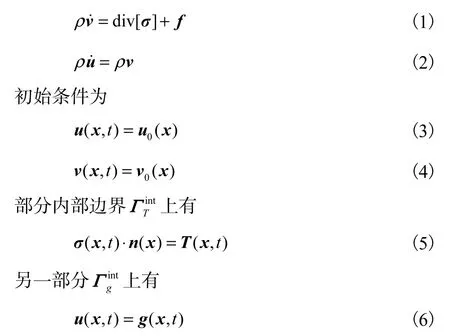
式中：ρ=ρ(x)为介质密度；f(x,t)为介质体力；u0(x)、v0(x)分别为初始位移和速度；σ(x,t)为应力张量；T(x,t)为Neumann边界条件中的外力；g(x,t)为Dirichlet边界条件中的位移；分别表示速度和位移对时间的偏微分；div[σ]=σij,j，σ·n=σijnj．

外部边界条件问题也早有研究．地球物理学在20世纪80年代由Bayliss和Turkel开始将数值近似算法应用于边界问题；20世纪90年代Givoli和Keller采用远场渐进展开，推导出非局部吸收边界条件已经被广泛采用．在此采用基于Engquist和Majda (1977)、Clayton和Engquist(1977)推导的旁轴条件的变分形式，在沿着人工边界部分采用弹性动力学方程有限波数扩张的方法，近似表示人工边界的瞬态阻抗．这种方法由Lysmet和Kuhlemeyer(1969)首次提出，对于高频波和较小入射角的波的反射有很高的精度．在人工边界extΓ，边界条件表示为

式中：t为边界上的力；n为边界指向外的法向量；vT=v-[v·n]表示速度在边界上的投影；cp和cs分别为P波和S波的传播速度．

2.2 控制方程的变分形式——弱形式

用数值的方法解决波动方程，可以采用弱积分表达式，使原始问题获得更广的数值解．首先引入测试函数空间ϕ

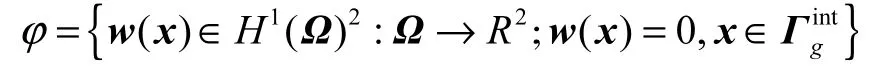
在方程(1)的两边同时乘以测试函数w(x)，同时联合边界条件，用分部积分法积分可得

这里有初始条件

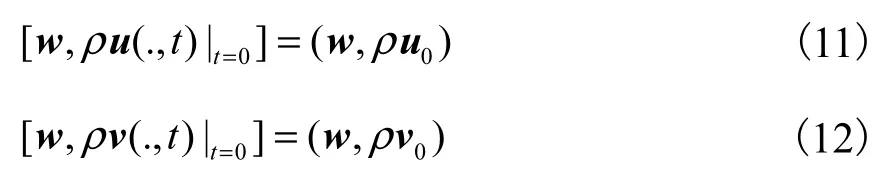
式中：a(.,.)表示初始应力虚功的双线性形式，表达式为

式中：c表示方程(9)中的弹性模量．

2.3 数值离散

像有限元中一样，谱元中也把计算区域离散为互不重叠的四边形单元：每个单元的测试函数表示为每个单元都映射到一个正方形参考域s，定义在2,[1,1] ΛΛ=-局部坐标系(ξ ,)η中．同时生成可逆的单元映射矩阵，坐标映射x=ϒe(ξ ,η)．

对于数值离散来说，应该保证变分形式满足分段多项式的近似空间，其中h表示基本单元网格的长度

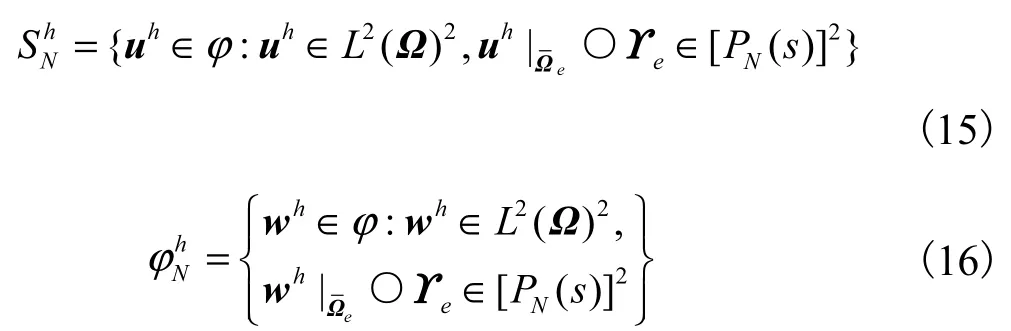
式中：L2(Ω)2为定义在Ω上的平方可积函数空间；[PN(s)]2为所有N阶多项式的张量空间．谱单元的离散空间可以用离散点(nel,N)表示，每个全局坐标域中的积分都使用局部坐标的张量积来表示．同时为了便于因式分解，(N+1)2个基点作为每个单元的积分点，这些积分点将单元划分为配置网格，设为，也就是(N+1)个Gauss-Lobatto-Legendre积分点的二维张量积．

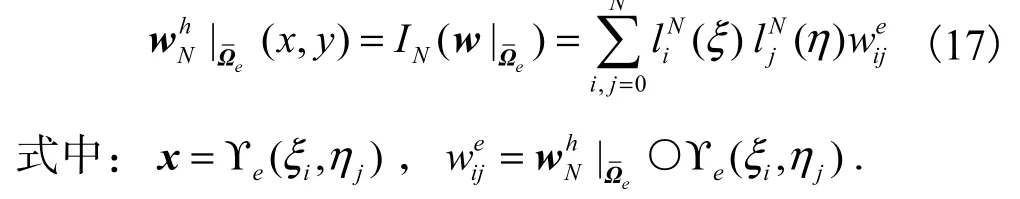
通过以上概述，它可以给出对于波动微分方程

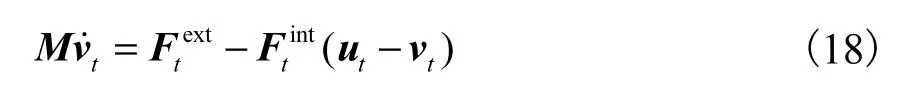
的耦合方法，其中ut和vt表示所有节点在t时刻的位移和速度向量，Fext表示外力矩阵，Fint表示内部节点力矩阵．谱方法由于Lagrange插值和GLL积分采用相同的配置点，所以得到对角质量矩阵M，大大降低了计算难度．

谱元法整合了有限元的几何模型的灵活性和谱技术的快速收敛性．由于谱元法的稳定性、GLL积分和插值的高精确度，通过设置Legendre多项式的阶数和划分单元数，可以使误差达到很高精度．本文的模型划分单元网格的长度为100,m，网格每条边上有8个插值点．

该方法通过参数α和β，迭代出离散动量方程在时间tn+a的位移速度和加速度

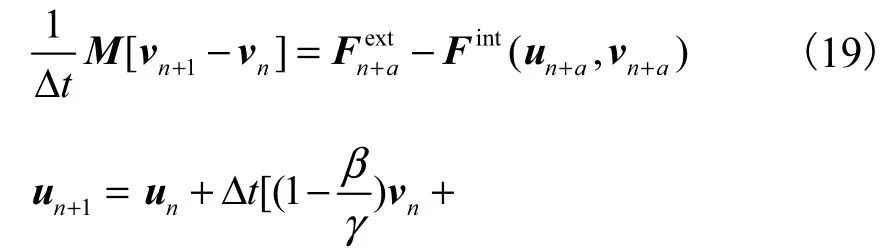
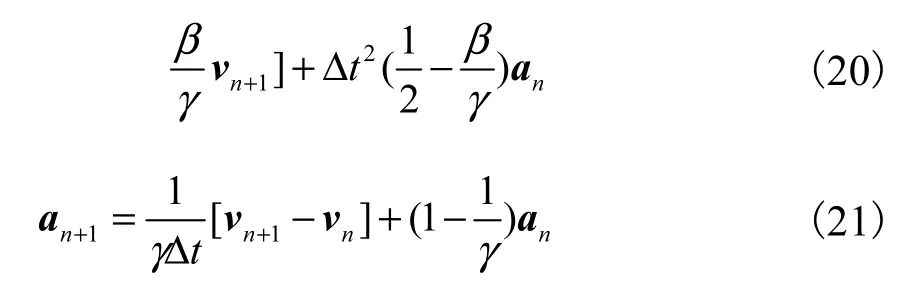
3 模型计算结果与分析

假设出平面线源埋深设置在地表下5,km，考虑到边界的影响，计算范围取5,R(R为盆地半径)，如图3所示．从不同发震主频率、不同剪切线源位置和不同的盆地形状来研究盆地地震响应，观察参数变化对地表地震动强度的影响．为便于对比，图4给出了无沉积盆地时，半空间地表在不同主频率波源作用下x＝0点处的位移时程曲线．假设半空间介质波速线性变化，波源在x＝0点正下方5,km处．图5给出了主频为1,Hz的出平面线源作用在不存在沉积(图5a)、存在沉积(R＝1,000,m，图5b)两种地形时，地表不同接受点的位移时程曲线对比．

图3 半圆形沉积盆地计算模型(R＝1,000,m)

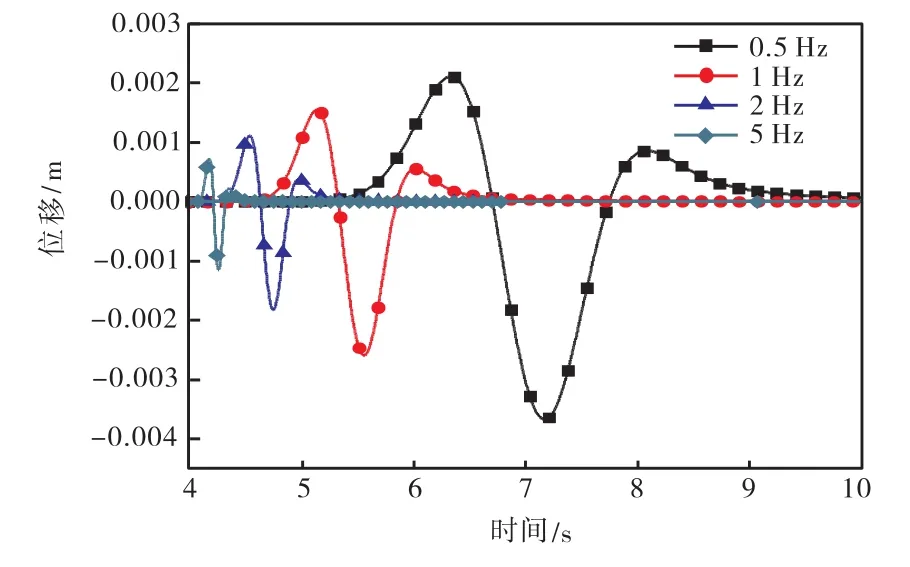
图4 无沉积盆地时x＝0点的位移时程曲线

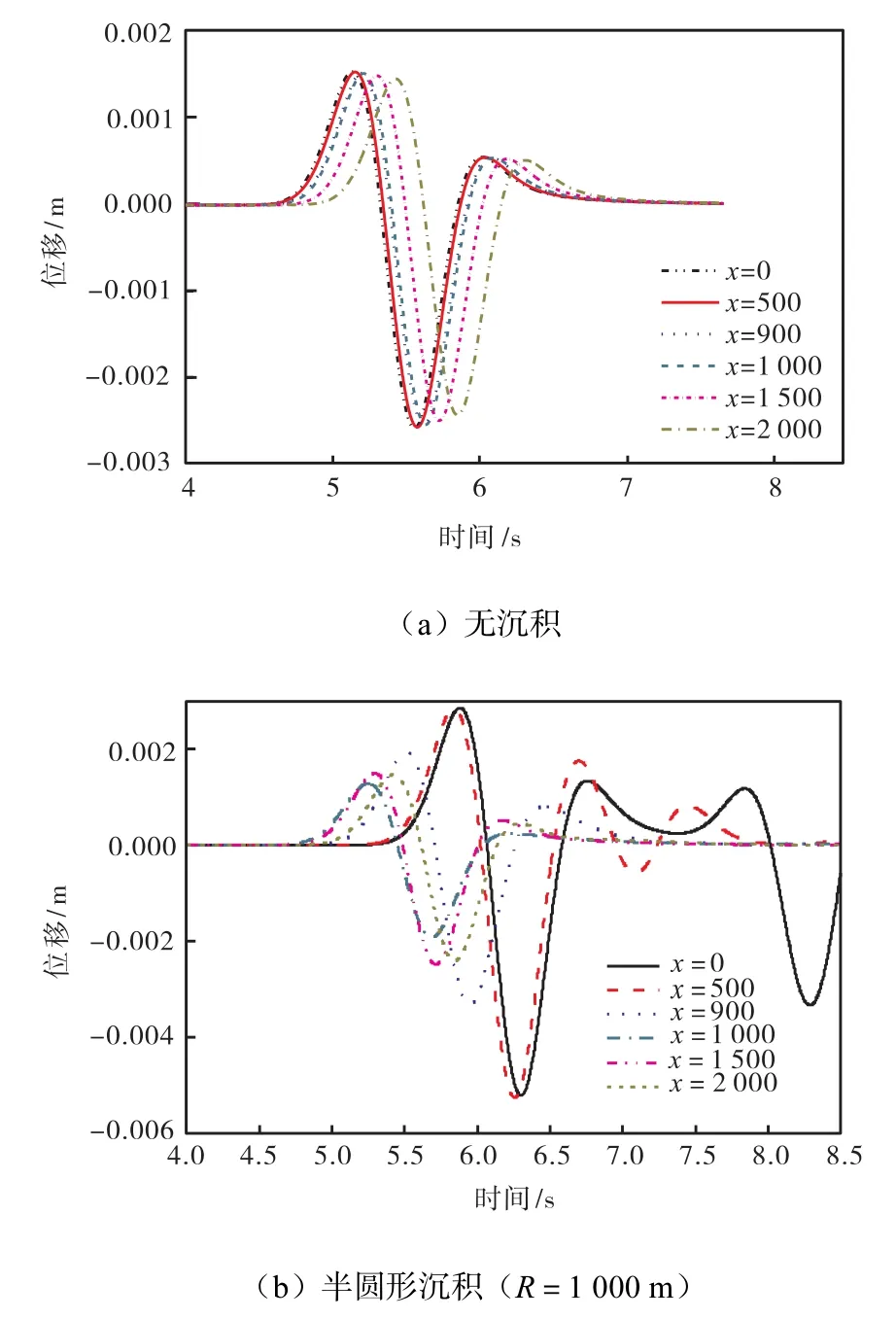
图5 地表不同接受点的位移时程曲线对比

3.1 不同主频率的点源的影响

以从沉积的正下方5,km入射Ricker子波为点源，主频率依次为0.5，1，2，5,Hz，其他参数相同．以R＝1,000,m的沉积盆地为研究对象，由于对称分布，选取地表横坐标为0，500，900，2,000,m为记录点，记录各点位移时程，结果如图6所示．

由图6对比可知：①沉积盆地对地震动有很强的放大效应，位移幅值最大达到没有沉积的2.3倍；②沉积场地的卓越频率在0.5～1.0,Hz，当频率＞1时，地表的位移幅值则随着频率的增加衰减很快，低频位移幅值达到高频位移幅值的2～4倍；③盆地的边缘效应比较明显，低频和高频位移幅值之比在边缘部分最大达到4倍；④沉积的存在对于沉积外的影响甚微，可以忽略．

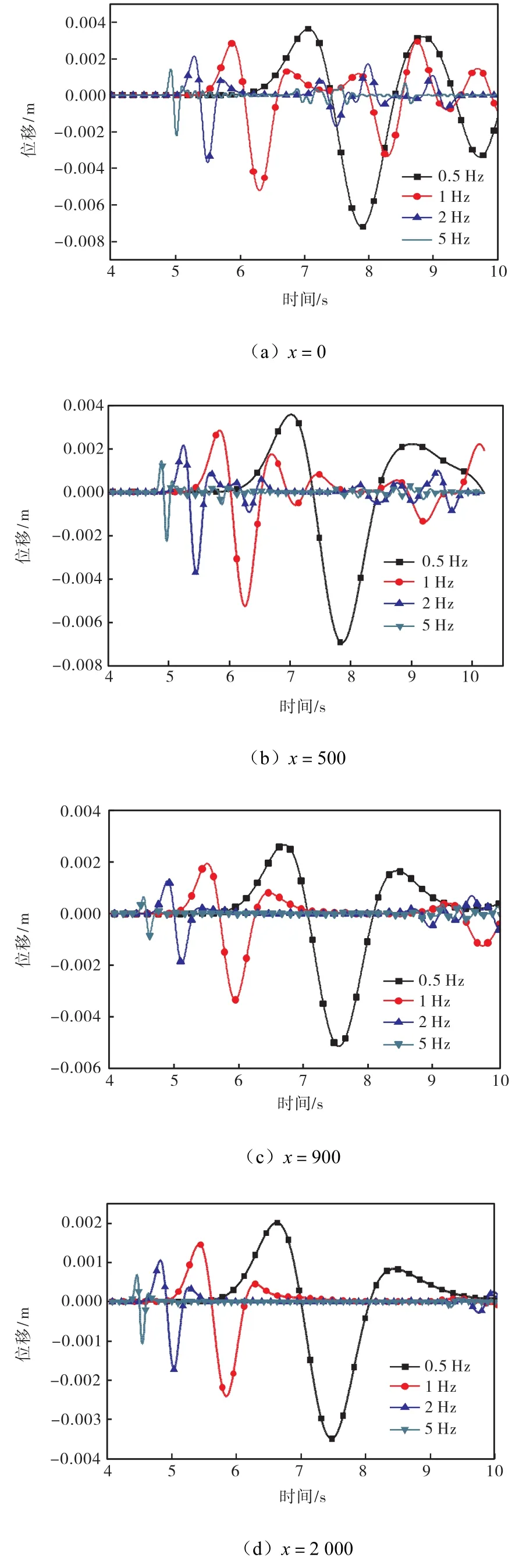
图6 地表不同接受点的位移时程曲线

3.2 不同点源位置对地表响应的影响

取主频为1,Hz的点源作用在埋深为5.0,km、水平坐标分别为0，500，800，1,000，1,500,m、沉积盆地半径为1,000,m的半圆形沉积上，分别做地表－2,000，－1,000，－900，0，900，2,000,m等处接受点位移时程曲线，如图7所示．

由图7可知，点源的水平位置的偏移对于地表各点的地震动影响较小，可能由于水平位移量相对于垂直埋深变化较小；但是由于沉积对地震波的阻抗，在x =－1,000,m处衰减最大，达到20%；x =－900,m处衰减了15%，其余点的衰减在10%以内．

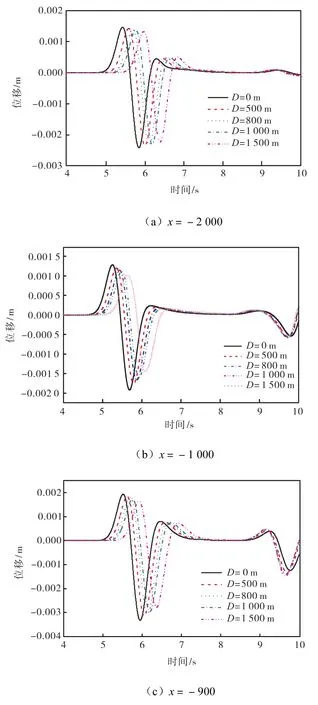
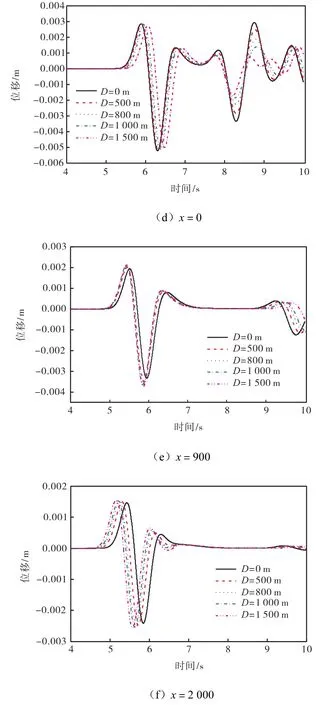
图7 不同震源偏移量时地表不同接受点的位移时程曲线

3.3 不同形状的盆地对其地震响应的影响

通过设置不同形状的盆地，模拟沉积地形对地震效应的影响．主要研究了如下参数的地形：① 半径为1,000,m的半圆形盆地；② a＝1,000,m，b＝500,m的浅椭圆形盆地；③ a＝1,000,m，b＝1,500,m的深椭圆形盆地，其示意见图8．沉积部分的波速在300～800,m/s间均匀变化；外部在深度3,km内，沿深度方向800～1,500,m/s均匀变化，震源采用1,Hz的主频出平面点源波源．不同地形在地表的位移曲线如图9所示．

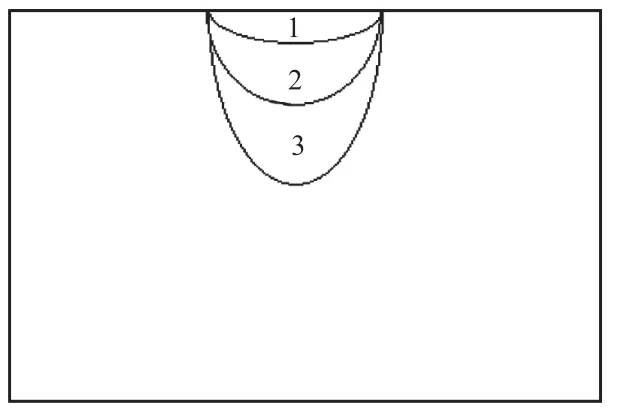
图8 地形示意图

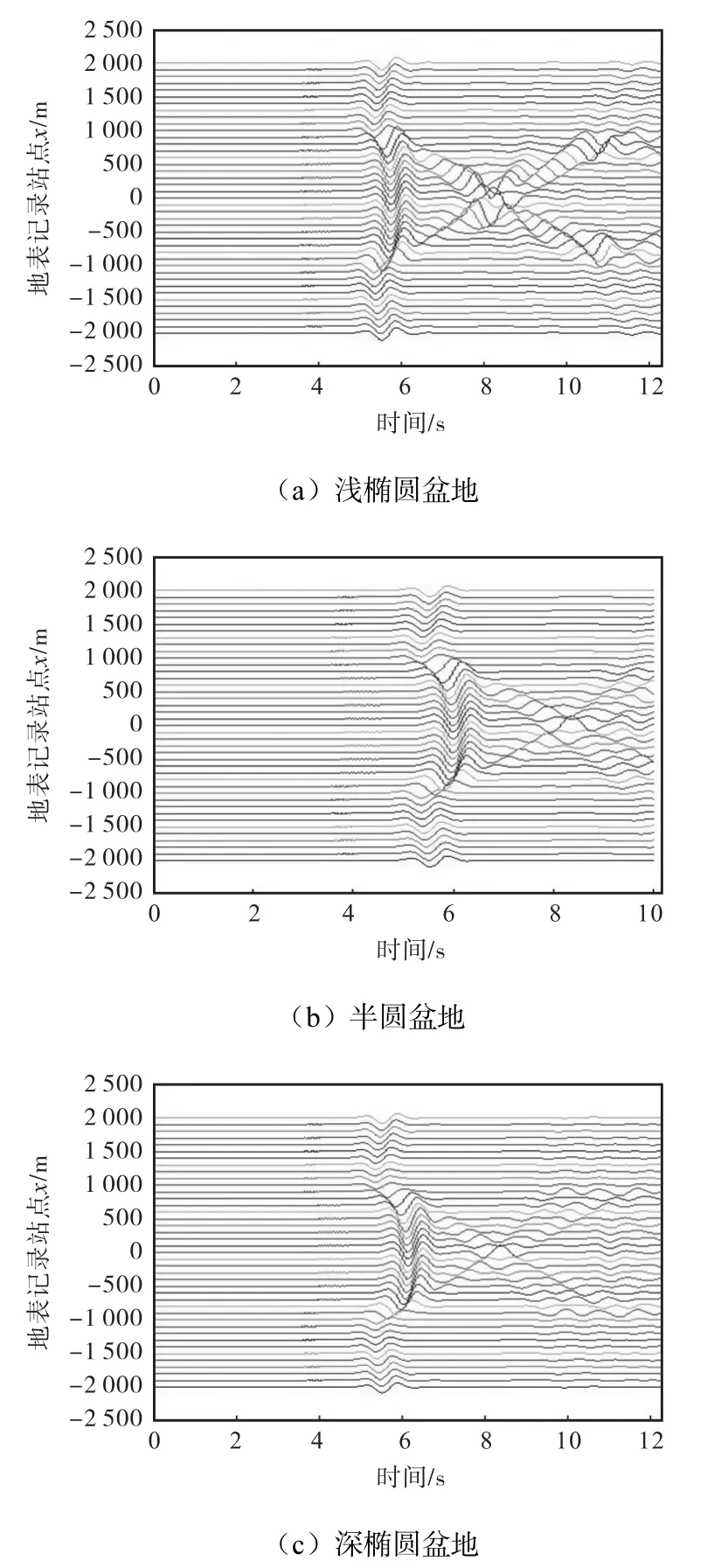
图9 地表记录站点在不同地形条件下合成的位移地震图

由图9模拟结果可知：①在地震波第一次到达中心点(x＝0)时，深椭圆盆地的位移振幅偏大，比浅椭圆盆地大20%；在第一次波谷到达中心之后，地震波能量由两边继续向中心传播，浅椭圆盆地能量消散相对较少，会再引起比较大的位移，而深椭圆盆地由于软土的阻抗作用，位移振幅相对较小；②盆地的边缘附近，浅椭圆盆地的响应要大，而且边缘内外地震影响差异很明显；内部有较大位移，外部相对平稳．这是由于边界的反射作用，地震波在边缘位置来回多次叠加，形成很明显的边缘效应．

4 结 论

(1)沉积盆地对地震动有很强的放大效应．

(2)地震波的频率和介质的频率相近时，地震动的响应强烈．

(3)盆地的边缘效应比较明显，在沉积盆地的外侧，基本不受沉积盆地的影响．

(4)对于半圆形沉积盆地来说，点源的相对位置的变化对盆地边缘两侧附近的影响较大，对其余点的影响很小．

(5)不同形状沉积盆地在出平面线源作用下，深椭圆盆地的地震响应较大，能量消散相对较快，由于介质边界对波的反射和折射，图像表现出明显的边缘效应．

(6)选取恰当的场地对建筑的抗震有很大作用，对于在沉积土层上的建筑物，比如天津的冲积土，应加强抗震设防，同一建筑物应避免建在不同的地质条件上．

［1］ 李雪强. 沉积盆地地震效应研究[D]. 哈尔滨：中国地震局工程力学研究所，2011：1-88.

［2］ 杜启振，杨慧珠. 方位各向异性粘弹性介质波场有限元模拟[J]. 地球物理学报，2003，52(8)：2,010-2,014.

［3］ KHAM M，SEMBLAT J F，BOUDEN-ROMDHANE N. Amplification of seismic ground motion in the tunis basin：numerical BEM simulations vs experimental evidences[J]. Engineering Geology，2013，155：80-86.

［4］ 王秀明，张海澜. 用于具有不规则起伏自由表面的介质中弹性波模拟的有限差分算法[J]. 中国科学，2004，34(5)：481-493.

［5］ 杨 莹. 二维地震波场有限差分法数值模拟研究[D].北京：中国地质大学，2009：1-48．

［6］ 刘有山，滕吉文，徐 涛，等. 三角网格谱元法地震波场数值模拟[J]. 地球物理学进展，2014，29(4)：1,715-1,726.

［7］ 刘启方，于彦彦，章旭斌. 施甸盆地三维地震动研究[J]. 地震工程与工程振动，2013，33(4)：54-60.

［8］ 李洪建，韩立国，巩向博. 复杂构造网格化及高精度地震波场谱元法数值模拟[J]. 石油物探，2014，53 (4)：375-383.

［9］ TENG Y C. Three-dimensional finite element analysis of waves in an acoustic media with inclusion[J]. J Acoust Soc,Am，1988，86：414-422.

［10］ MARFURT K J．Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equation[J]. Geophysics，1984，49：533-549.

［11］ MADARIAGA R．Dynamics of an expanding circular fault[J]. Bull Seism Soc Am，1976，65：163-182.

［12］ LEVANDER A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics，1988，53：1,452-1,463．

［13］ ORSZAG S A．Spectral methods for problems in complex geometries[J]. J Comput Phys，1980，37：70-92.

［14］ PATERA A T. A spectral element method for fluid dynamics：laminar flow in a channel expansion[J]. J Comput Acoust，1994，2(4)：371-422.

［15］ 陈敬国. 波场模拟中的震源—Ricker子波浅析[EB/OL]. 北京：中国科技论文在线，2006[2014-09-10]. http：//www. paper. edu. cn/html/releasepaper/ 2006/07/105/

［16］ 王童奎，李瑞华，李小凡，等. 谱元法数值模拟地震波传播[J]. 防灾减灾工程学报，2007，27(4)：470-477.

［17］ DIMITRI K，JEAN-PIERRE V．The spectral element method：an efficient tool to simulate the seismic response of 2D and 3D geological structures[J]. Bulletin of the Seismological of America，1998，88(2)：368-392.

［18］ DIMITRI K，JEAN-PIERRE V．The spectral element method for elastic wave equations application to 2-D and 3-D seisnic problems[J]. International Journal for Numerical Methods in Engineering，1999(45)：1,139-1,164.

［19］ DAUKSHER W，EMERY A F. The solution of elastostatic and elastodynamic problems with Chebyshev spectral fnite elements[J]. Comput Methods Appl Mech Engrg，2000(188)：217-233.

The Research of Seismic Response of the Sedimentary Basin Under the Anti-plane Shear Line Source Based on the Simulation of the Spectral Element Method

HAN Jian-bin，LIU Zhong-xian，LUO Zhao-hui
(School of Civil Engineering，Tianjin Chengjian University，Tianjin 300384，China)

Due to the difference of the medium impedance between the internal and external of basin,and the special geometric shapes of basin,there is a remarkable ground motion amplification effect in the basin. In this thesis,the spectral element method has been used to study the effect of the seismic response of the sedimentary basin caused by different main frequency of anti-plane shear line sources,different point source location,and different sedimentary shapes. The result shows that the frequencies of point source and sedimentary shape have greater influences on the surface response. A different position of the point source for the edge effect has a certain influence.

sedimentary basin；anti-plane shear line source；spectral element；seismic response

TU435；P315.31

A

2095-719X(2015)02-0077-07

2014-10-14；

2014-12-01

国家自然科学基金(51278327)

韩建彬（1988—），男，河北石家庄人，天津城建大学硕士生.