一类不确定分数阶混沌系统自适应同步与参数辨识

赵小山，孔德富，郭永峰

（1.天津职业技术师范大学理学院，天津 300222；2.天津工业大学理学院，天津 300387）

一类不确定分数阶混沌系统自适应同步与参数辨识

赵小山1，孔德富1，郭永峰2

（1.天津职业技术师范大学理学院，天津 300222；2.天津工业大学理学院，天津 300387）

针对一个参数不确定的分数阶混沌系统，首先给出不同相平面上的混沌吸引子图，然后基于分数阶系统稳定性理论，设计了一种自适应同步控制方法，不仅能够实现该系统的混沌同步，同时能够完成响应系统的参数辨识，并根据Lyapunov稳定性理论给予严格证明，最后通过数值仿真，验证了该方法的有效性和正确性.

分数阶混沌系统；混沌同步；参数辨识；自适应同步；控制器

分数阶微积分理论尽管有300多年的历史，但是因为其长时间没有实际应用背景而发展缓慢[1].但近几十年来，由于Mandelbort[2]提出自然界乃至很多科学领域都存在分数维的事实，分数阶微积分得到了迅猛的发展.在混沌系统的同步中，参数具有极其重要的作用，当系统中某些参数未知时，混沌系统的敏感性将造成系统状态极大的差异.目前很多研究者已经对整数阶的参数问题进行了大量的研究[3-4]，但对分数阶混沌系统的参数识别问题研究相对较少.在很多实际应用中，分数阶系统又能更准确地反映其数学特性，因而逐渐成为混沌研究的热点.自1990年，Pecora和Corroll首次提出混沌同步的概念以来，人们从不同的角度实现了不同类型的混沌同步，有完全同步、广义同步、投影同步等[5-7].本文针对一个不确定的分数阶混沌系统，设计自适应控制器并进行参数识别，最后通过数值模拟验证该方法的有效性和正确性.

1 分数阶微积分的定义及算法

分数阶微积分存在着多种定义，大多采用的是Caputo定义和Riemann-Liouville（R-L）定义，本文采用的是Caputo定义[8]：

式中：m=[α]；Jθ为θ阶Riemann-Liouville积分算子，它被定义为：

其中Γ（·）为Gamma函数.

预估-校正算法是典型的求解一阶微分方程组Adams-Bashforth-Moulton[9]法的推广，基于Caputo分数阶微分定义，将其应用到分数阶系统的数值计算.

考虑下面的初值问题

在文献[10]中，Diethelm等证明了如果方程f是连续的，那么（3）式的初值问题等价于如下的Volterra积分方程

令h=T/N，tn=nh，n=0，1…，N∈Z+，首先进行Adams-Bashforth预估，得到如下公式

其相应的预估矫正算法误差为maxj=0，1，…N|x（tj）-xh（tj）|=O（hp），其中p=min（2，1+α）.

2 混沌行为

超混沌Lorenz-Stenflo（LS）系统是Stenflo在研究低频率短波长的重力波方程式提出来的，其形式如下：

式中：x、y、z、w为系统的状态变量；a、b、c、d为系统参数，当a=1，b=7，c=26，d=1.5时，系统存在混沌吸引子.

本文研究的是系统（8）分数阶的形式.其分数阶形式为：

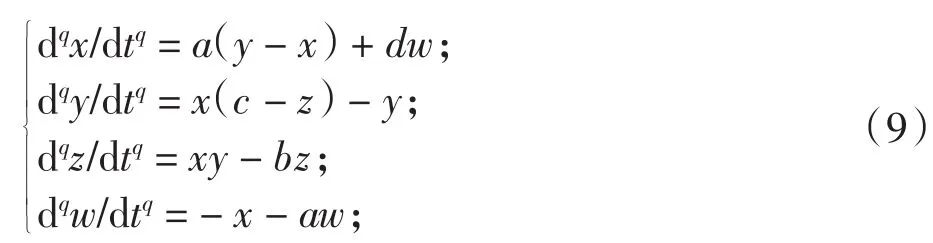
式中：q为分数阶系统的阶数，q=0.98，分数阶系统的参数依然取a=1，b=7，c=26，d=1.5.采用Caputo定义设计算法，利用Matlab数值仿真，得出系统（9）的混沌吸引子图如图1所示.

图1 系统（9）混沌吸引子图Fig.1 Chaotic attractor of system（9）

通过这个在二维平面上的相图更加可以清晰的看出该系统的混沌轨道是双漩涡结构.

3 参数未知的混沌系统自适应同步与参数辨识

文献[11]给出了分数阶稳定性理论.

定理1 考虑线性分阶系统

式中，0＜q＜1，x∈Rn（n∈N），A∈Rn×n.当且仅当矩阵A的任意特征值λ，满足|arg（λ）|＞qπ/2时，系统（10）渐近稳定.

由定理1的证明过程可以得出如下定理2.

定理2 对于非线性分数阶系统

式中，0＜q＜1，x=（x1，x2…，xn）T，A（x）∈Rn×n为状态向量，是系数矩阵.当含有状态变量的系数矩阵A（x）的所有特征值λi（i=1，2，…，n）实部都不大于零，即|arg（λi）|＞qπ/2时，系统（11）是渐近稳定的.

根据分数阶稳定性理论，设计如下自适应同步同步控制方法，并进行参数辨识.

本文设驱动系统为：

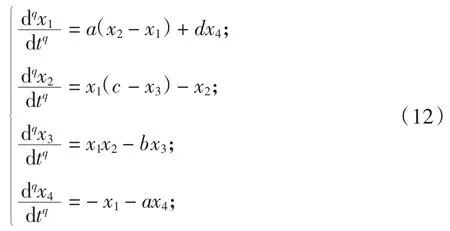
假设所有参数均为未知，采用自适应同步方法，设计如下响应系统：

同步误差变量设为：e1=y1-x1，e2=y2-x2，e3=y3-x3，e4=y4-x4，未知参数估计误差设为：

定理3 若设计的系统同步控制器为

则t→∞时，误差动力系统（16）趋于稳定，即驱动系统（12）和响应系统（13）达到同步.

证明 针对误差动力系统（16），构造如下的Lyapunov函数：

4 数值模拟

由预估-校正算法，结合Matlab进行数值仿真，参数a，b，c，d的真实值分别为（a，b，c，d）=（1，0.7，26，1.5）；驱动系统（12）的初始值为（x1（0），x2（0），x3（0），x4（0））=（0.1，0.2，0.2，-0.2）；响应系统（13）的初始值为（y1（0），y2（0），y3（0），y4（0））=（15，20，10，40）；误差系统（16）的初始值为（e1（0），e2（0），e3（0），e4（0））=（14.9，19.8，9.8，40.2）；参数估计值分别为=（10，-5，0，10），得到误差系统变化曲线和参数辨识效果.图2为误差系统（16）的误差变化曲线.

图2 误差系统（16）时间历程图Fig.2 Synchronization errors of systems（16）

由图2可以看到，随着时间t的增加，系统同步误差逐渐为0，也就是驱动系统（12）和响应系统（13）达到同步.图3为未知参数辨识图，其中（a）、（b）、（c）、（d）是参数a、b、c、d的辨识曲线.

图3 未知参数辨识图Fig.3 State trajectories of unknown parameters

由图3可以看出，当参数a、b、c、d分别从估计值10、-5、0、10快速的趋近于真实值1、0.7、26、1.5，也就是说，所设计的辨识规则是正确的.

5 结束语

本文针对参数不确定的分数阶超混沌Lorenz-Stenflo系统，给出了其在不同相平面上的混沌吸引子图；基于分数阶稳定性理论，设计了合适的自适应同步控制器，根据Lyapunov稳定性定理，推导出未知参数的辨识规则，通过利用预估-校正算法，进行数值模拟，验证了该方法的有效性和正确性.该方法也可以推广到其他分数阶混沌系统中，同时分数阶混沌系统异结构同步与参数辨识，甚至分数阶混沌系统异结构投影同步与参数辨识，将在接下来的工作中进一步研究.

[1]刘崇新.蔡氏对偶混沌电路分析[J].物理学报，2002，51（6）：1198-1202.

[2]LORENZ E N.Deterministic nonperiodic flow[J].J Atmos Sci，1963，20：130-141.

[3]SUNDARAPANDIANV，PEHLIVANI.Analysis，control，synchronization，and circuit design of a novel chaotic system[J]. Mathematical and Computer Modeling，2012，55：1904-1915.

[4]YUAN L，YANG Q.Parameter identification and synchronization of fractional-order chaotic systems[J].Communications in Nonlinear Science and Numerical Simulation，2012，17：305-306.

[5] 董俊，张广军，姚宏.异结构超混沌系统的完全同步与反相同步控制[J].空军工程大学学报，2012，13（5）：90-94.

[6]王兴元，孟娟.一类混沌神经网络的观测器广义投影同步设计[J].应用力学学报，2008，25（4）：656-659.

[7]MAINIERIR，REHACEKJ.Projectivesynchronizationin threedimensional chaotic systems[J].Physical Review Letters，1999，82（15）：3042-3045.

[8]CAPUTO M.Linear models of dissipation whose q is almost frequency independent-II[J].Geophysical Journal of the Royal Astronomical Society，1967，13（5）：529-539.

[9]DIETHELM K，FORD N J，FREED A D.A predictor-corrector approach for the numerical solution of fractional differential equations[J].Nonlinear Dynamics，2002，29：3-22.

[10]DIETHELM K，FORD N J.Analysis of fractional differential equations[J].Math Anal Appl，2002，265：229-248.

[11]张若洵，杨世平，刘永利.基于线性控制的分数阶统一混沌系统的同步[J].物理学报，2010，59（3）：1549-1552.

[12]HAHN W.The Stability of Motion[M].New York：Springer Press，1967.

Adaptive synchronization and parameter identification of one class of uncertain fractional-order chaotic system

ZHAO Xiao-shan1，KONG De-fu1，GUO Yong-feng2
（1.School of Science，Tianjin University of Technology and Education，Tianjin 300222，China；2.School of Science，Tianjin Polytechnic University，Tianjin 300387，China）

In view of one parameter uncertain fractional-order chaotic system，firstly，the chaotic attractors of different phase plane are given.Then，based on the fractional-order stability theory，suitable adaptive synchronization controllers are designed.The method not only achieves the chaos synchronization of the system，but also identifies unknown parameters of the respond system.At last based on the Lyapunov stability theory，strict mathematic proof is given，numerical simulation demonstrates the effectiveness and correctness of the method.

fractional-order chaotic system；chaos synchronization；parameter identification；adaptive synchronization；controller

O231.2

A

1671－024X（2015）03－0085－04

10.3969/j.issn.1671-024x.2015.03.018

2015-01-23

国家自然科学基金资助项目（11302158，11302148）；天津职业技术师范大学研究生创新基金资助项目（YC14-14）

赵小山（1967—），男，副教授，研究方向为非线性动力系统分析.E-mail：xszhao678@126.com