结合自适应遗传算法与弹性BP神经网络的亚硝酸盐预测模型

林志贵，姚芳琴，冯林强，杜军兰，李建雄

（1.国家海洋技术中心 近海海洋环境观测与监测技术研究室，天津 300112；2.天津大学精密仪器与光电子工程学院，天津 300072；3.天津工业大学电子与信息工程学院，天津 300387）

结合自适应遗传算法与弹性BP神经网络的亚硝酸盐预测模型

林志贵1，2，3，姚芳琴3，冯林强1，杜军兰1，李建雄3

（1.国家海洋技术中心 近海海洋环境观测与监测技术研究室，天津 300112；2.天津大学精密仪器与光电子工程学院，天津 300072；3.天津工业大学电子与信息工程学院，天津 300387）

针对目前营养盐检测主要是通过化学方法实现，无法获得在线检测的问题，利用营养盐与其影响因子之间的关系，提出结合自适应遗传算法与弹性BP神经网络的预测模型.利用改进的自适应遗传算法，通过交叉、变异获取弹性BP神经网络的初始权值与阈值，加速预测过程.该模型通过营养盐影响因子数据，预测亚硝酸盐浓度.仿真结果表明：基于弹性BP神经网络的预测模型预测营养盐浓度是可行的，其预测得到的亚硝酸盐浓度值的相对误差主要集中于0～30%；结合自适应遗传算法与弹性BP神经网络的预测模型的预测效果好于基于弹性BP神经网络的预测模型.

亚硝酸盐；预测；自适应遗传算法；弹性BP神经网络

海水中营养盐的运移和转化过程是海洋生态系统中的一个重要过程，其不同浓度和组成，对海洋的初级生产力产生影响，并对动植物的群落结构产生调节作用，影响到整个海洋生态系统的结构.营养盐贫泛时，营养盐不足以维持浮游植物的生长，浮游植物就会大大降低.营养盐过剩时，营养盐会使某种浮游植物过度繁殖，破坏浮游植物的群体结构，导致生态系统呈富营养态，甚至赤潮发生.近海海域受工业生产及人类生活影响较大，其海水中的营养盐浓度和组成变化较大.这种变化不仅反映了营养盐状况的变化，同时反映了海水中营养盐的再生、循环机制的改变，对海区生态环境产生较大的影响.

目前，区域水域营养盐的检测经历了实验室测定法、现场非在线检测、单个营养盐的在线检测及分析预测和多个营养盐的在线检测及分析预测4个阶段.实验室测定法[1]存在着化学反应时间长、试剂用量大、化学试剂的稳定性差等缺点，且测定采用手工方法，造成效率低、准确度差、稳定性不高等问题[2].营养盐现场非在线检测阶段提高了检测精度和省去了人工对营养盐化学反应的干预，但不能提供连续数据，花费较大的人力、物力、财力；且检测手段也是通过化学方法实现的.该方法具有投资小、操作简便的优点，但检出限高、灵敏度较低[3-4].单个营养盐的在线检测及分析预测阶段利用单营养盐分析仪采集数据，并将其通过总线送给远程终端，实现对营养盐的在线检测.随着营养盐预测研究的不断深入，营养盐分析仪由检测单参数的发展为检测多参数，提高了集成度，实现对多种营养盐的检测.相应地，营养盐的在线检测也由单营养盐发展为多营养盐的在线检测.如有学者[5]建立了一套基于PROFIBUS-DP现场总线的PLC控制海水营养盐自动分析系统，该系统采用化学方法实现营养盐的检测，通过有线方式传输数据.这种方法因人为因素易带来数据误差.

上述检测方法都是点检测，并且测量方法是通过化学方法实现的，无法在线获得区域水域营养盐的连续分布情况.有学者[6]利用不同波段遥感图像数据进行反演，间接获取营养盐数据，得到了除磷酸盐以外的其他4种盐的单参数线性拟合函数，但营养盐测定的精度不高、花费高，而且受到天气、海况以及卫星过境时间等多种因素影响.近年来，国内外开展了大量关于营养盐变化及限制因子的研究[7-14]，研究表明，营养盐的赋存状态与其他水体环境因子之间存在着双向的内在联系：水体的环境因子影响着营养盐的水平和赋存状态，营养盐的水平和状态的改变将在一定程度上改变了水体的理化性质，进而影响着水体中其他物质的形态分布.因此，本文分析亚硝酸盐与其影响因子间的数据特点，引入人工智能方法，结合自适应遗传算法与弹性BP神经网络，建立一种亚硝酸盐预测模型.基于该模型，由亚硝酸盐影响因子数据间接预测区域水域的亚硝酸分布情况，为近海海域生态系统平衡管理及渔业生产规划提供依据，也为其他无法测量的海水参数（如有机物、重金属等）提供了一种新的测量方法.

1 相关理论基础

1.1 弹性BP神经网络

BP神经网络[15]由输入信号的正向传播和误差信号的反向传播构成.其基本原理是：在信号正向传播中，输入信号从输入层传入，经过隐含层的一系列变换后，将得到的结果传向输出层，在输出层经运算后产生输出信号.通过比较输出层各个神经元的实际输出与期望输出，获得两者间的误差，若误差未能满足设定的精度要求或未达到预先设定的迭代次数，则转入误差的反向传播过程，对误差进行反向调节.在误差的反向传播中，误差信号从输出层以某种方式逐层向前传播，并逐层修正各个权值与阈值，最后回到输入层.通过反复的信号的正向传播和误差的反向调节，神经元间的权值与阈值得到不断的调节和修正.当输出信号的误差满足设定的精度要求或达到预先设定的学习次数时，停止学习.

BP神经网络的隐含层通常采用S型激励函数，当输入很大时，可能导致算法中的梯度幅值很小，造成修正权值的过程停滞不前.针对这一问题，弹性BP算法当连续两次迭代的梯度方向相同时，将权值与阈值的修正量乘以增量因子，增加修正值；当连续两次迭代的梯度方向相反时，将权值与阈值的修正量乘以减量因子，减小修正值；当梯度幅值为零时，则保持修正值固定不变，从而克服梯度幅度的不利影响.权值与阈值修正量的调节如公式（1）所示：

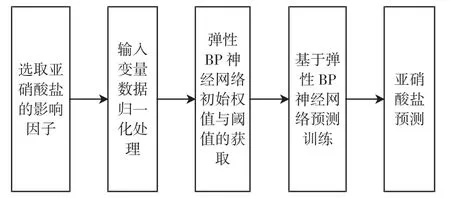
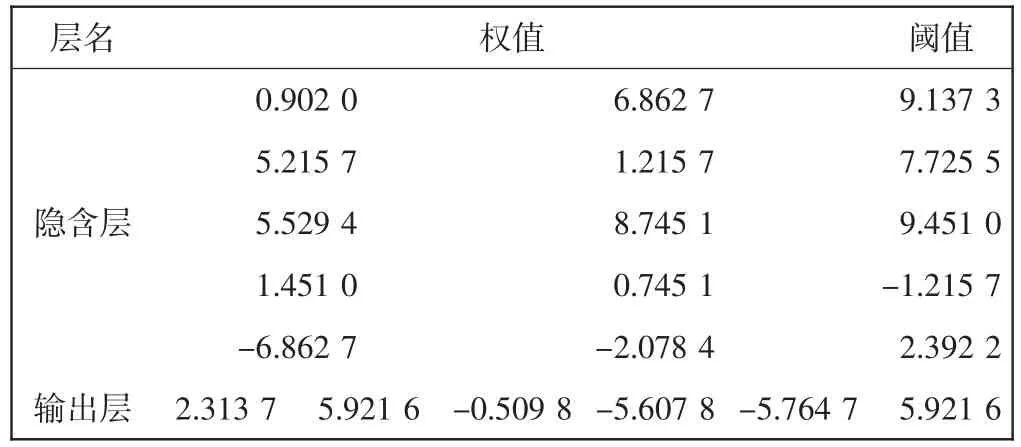
式中：g（n）为第n次和第n+1次迭代的变化梯度；w（n+1）和w（n）分别表示第n次和第n+1次迭代的权值修正量；kwinc为权值增量因子，其取值一般选为1.2；kwdec为权值减量因子，0

弹性BP神经网络通常由输入层、隐含层和输出层三层结构组成，根据Kolmogorov定理，具有一个隐含层（隐含层节点足够多）的三层BP神经网络能在闭集上以任意精度逼近任意非线性连续函数.因此，本文采用单隐含层的BP神经网络结构，构建亚硝酸盐与其影响因子间关系模型.

1.2 改进的自适应遗传算法

遗传算法（GA）[16]首先随机选取一种群作为初始种群，再对该初始种群进行随机选择操作、交叉操作和变异操作，让新产生的种群进化到搜索空间中更好的区域中，按照上述过程对种群进行不断的优化，使该种群进化成一个最能适应环境的种群，这一过程就是一个寻求最优解的过程.在寻优过程中存在一定的随机性和盲目性，导致搜索后期在局部最优解的附近停滞不前，群体进化速度减慢，甚至出现不进化现象，最终找不到最优解.其随机性和盲目性主要体现在固定参数的设置上，尤其是固定的交叉概率和变异概率.因此，为了避免过早收敛，改善算法收敛性，常常采用适当的交叉和变异提高其性能.

在遗传算法的执行过程中，依据个体的具体进化情况，自适应地改变交叉和变异概率的大小，这样得到的算法就是自适应遗传算法.其基本思想是：当种群中的个体的适应度比较分散时，则减小交叉和变异概率，使得优良个体得以生存；当种群中各个体的适应度值趋于一致或趋于局部最优解时，则增大交叉和变异概率，从而跳出局部最优解的状态.

自适应遗传算法在交叉概率和变异概率自调整的过程中，当适应度值越接近最大适应度值时，交叉概率和变异概率就越小；当等于最大适应度值时，交叉概率和变异概率的值为零.这种自适应的调整方法增大了局部最优解发生的可能性.而且，亚硝酸盐的影响因子的实际采样中可能存在误差，以及环境因素，造成初始数据误差较大，如果直接使用传统的自适应遗传算法进行数据处理，效果不理想.出于此目的，在自适应遗传算法的基础上，对自适应遗传算法的交叉概率Pc和变异概率Pm做了进一步的改进，使群体中最大适应度值的个体的交叉概率和变异概率不为零，分别提高到某个设定的值（如Pc2、Pm2），这样，相应的提高群体中的优良个体的交叉概率和变异概率.这种改进的自适应遗传算法的交叉概率Pc和变异概率Pm如公式（2）、公式（3）所示.

式中：f′为交叉的两个个体中较大的适应度值；f为变异的个体的适应度值；favg为群体的平均适应度；Pc1取0.9 ，Pc2取0.6，Pm1取0.1，Pm2取0.001.

因此，本文采用一种改进的自适应遗传算法，确定弹性BP神经网络的初始权值与阈值.利用改进的自适应遗传算法弥补弹性BP神经网络连接权值和阈值选择上的随机性缺陷，不仅能发挥弹性BP神经网络泛化的映射能力，而且使弹性BP神经网络具有很快的收敛性以及较强的学习能力.

2 结合自适应遗传算法与弹性BP神经网络的预测模型

基于亚硝酸盐及其影响因子数据，利用改进的自适应遗传算法优化弹性BP神经网络的权值与阈值，将优化的权值与阈值作为弹性BP神经网络的初始权值与阈值，用于弹性BP神经网络的训练；训练得到的最佳网络用于预测亚硝酸盐，具体结构如图1所示.

图1 亚硝酸盐预测模型结构Fig.1 Structure of anitrite prediction model

（1）选取亚硝酸盐的影响因子.亚硝酸盐的主要影响因子有盐度、pH值、溶解氧（DO）、叶绿素、温度等参数.本文选用pH值和DO作为预测模型的输入变量，研究亚硝酸盐与pH、DO间非线性关系.

（2）输入变量数据归一化处理.输入变量数据的量纲不同，以及BP神经网络激励函数的输出一般都在（-1，1）之间，因此需要对输入变量数据进行归一化处理，使其全部处于（-1，1）之间.归一化处理如公式（4）所示.

式中：X为归一化后的输入值；Xmax和Xmin为输入变量的最大值和最小值；Xi为输入变量的实际值.

（3）弹性BP神经网络初始权值与阈值的获取.基于改进的自适应遗传算法，获取弹性BP神经网络初始权值与阈值.首先，确定遗传策略，包括选择群体大小、最大代数、交叉概率、变异概率等遗传参数；选择编码策略，对参数集合进行编码，本文采用二进制编码方式，对权值与阈值的染色体进行编码.其次，定义适应度函数并随机产生初始化群体，本文将亚硝酸盐的输出值与实际值差的平方的倒数之和定义为适应度函数.紧接着，计算群体中所有个体的适应度值.然后，按照确定的遗传策略，对群体进行选择、交叉和变异操作，形成新的群体.最后，判断新产生群体的性能是否满足指定的指标，或者已达到预定的迭代次数，最终得到最大适应度个体的权值与阈值.将其作为弹性BP神经网络的初始权值与阈值.

（4）基于弹性BP神经网络预测训练.基于改进的自适应遗传算法，通过交叉、变异获取弹性BP神经网络初始权值与阈值；训练弹性BP神经网络，对每次的训练结果进行比较，直至获得预测误差较小的网络模型，停止训练，保存网络参数，得到预测模型.

（5）亚硝酸盐预测.依据上述的预测模型，结合亚硝酸及其影响因子数据，预测亚硝酸的浓度值.

亚硝酸盐预测模型的流程图如图2所示.

图2 亚硝酸盐预测模型的流程图Fig.2 Flow chart of a nitrite prediction model

3 预测模型仿真及分析

仿真平台是VS2008和MATLAB 2010a[17]，实验总共使用90组数据，90组数据归一化处理后得到的数据见表1，其中，前72组数据用于预测模型的训练，后18组数据用于预测模型的预测.

表1 实验数据（归一化后的数据）Tab.1 Experimental data（normalized data）

三层BP神经网络的输入层为2个节点，即DO和pH值；输出层为1个节点，即亚硝酸盐值.通过多次训练，获得当隐含层为5个节点时，效果最佳，所以，本文最后确定为隐含层为5个节点.

本文仿真实验从2个方面进行：一是基于附加动量BP神经网络的预测模型和基于弹性BP神经网络的预测模型仿真训练及其比较分析；另一个是基于弹性BP神经网络的预测模型和结合自适应遗传算法与弹性BP神经网络的预测模型仿真训练及其比较分析.

（1）基于附加动量BP神经网络的预测模型和基于弹性BP神经网络的预测模型仿真训练及其比较分析.分别基于附加动量BP神经网络和弹性BP神经网络构建预测模型，结合实验数据，实验得到权值与阈值如表2、3所示；基于这2个模型预测亚硝酸盐浓度的相对误差如图3所示.

表2 附加动量BP神经网络模型的权值和阈值Tab.2 Weights and thresholds of additional momentum BP neural network

表3 弹性BP神经网络模型的权值和阈值Tab.3 Weights and thresholds of elastic BP neural network

图3 附加动量和弹性BP网络方法建立的亚硝酸盐预测模型的相对误差图Fig.3 Relative error of nitrite prediction models based on additional momentum BP neural network and based on elastic BP neural network

通过分析可知，基于附加动量BP神经网络预测模型的均方误差达到0.111时，需要迭代10 000次，花费的时间长达78 s；基于弹性BP神经网络构建预测模型的均方误差达到0.110时，需要迭代16次，花费的时间很短，不到1 s，明显好于前者.从图3看出，基于这2种模型得到的亚硝酸盐浓度值的相对误差主要集中在0%～30%，因而可得，将BP神经网络运用亚硝酸盐的预测具有可行性.

（2）基于弹性BP神经网络的预测模型和结合自适应遗传算法与弹性BP神经网络的预测模型仿真训练及其比较分析

遗传算法的初始参数如下：种群大小为200，最大代数为1 000，交叉概率Pc为0.8，变异概率Pm为0.05；弹性BP神经网络选为节点数为2-5-1的三层结构，网络的权值与阈值的范围为-10～10.网络的权值与阈值的染色体字节长度=21（2*5+5*1+5+1=21）；相应地，染色体长度为168（8*21=168）.

弹性BP神经网络的权值与阈值如表3所示；结合改进的自适应遗传算法优化弹性BP神经网络（AGA）的权值与阈值如表4所示.将表4中的权值与阈值作为弹性BP神经网络的初始权值与阈值，训练预测模型，训练得到的权值与阈值如表5所示.基于这2个网络构建的亚硝酸盐预测模型的相对误差如图4所示.

表4 AGA仿真得到的权值和阈值Tab.4 Weights and thresholds obtained by AGA

表5 AGA优化后的弹性BP神经网络训练得到的权值和阈值Tab.5 Weights and thresholds obtained by Elastic BP neural network optimized by AGA

通过网络训练可得：2种方法的训练时间都在1 s之内.由图4可知，基于这2种预测模型，得到的亚硝酸盐浓度值的相对误差主要集中在0%～30%，弹性BP神经网络方法得到的均方误差为0.110，改进的自适应遗传算法优化弹性BP神经网络方法得到的均方误差为0.087 3，其均方误差比前者小.结合自适应遗传算法与弹性BP神经网络的预测模型的预测结果好于基于弹性BP神经网络的预测模型.

图4 弹性BP网络和AGA优化弹性BP网络方法建立的亚硝酸盐预测模型的预测结果相对误差图Fig.4 Relative error of nitrite prediction models based on elastic BP neural network and based on elastic BP neural network optimized by AGA

4 结束语

从基于附加动量BP神经网络的预测模型和基于弹性BP神经网络的预测模型仿真，以及基于弹性BP神经网络的预测模型和结合自适应遗传算法与弹性BP神经网络的预测模型两方面，做实验仿真，得到亚硝酸盐预测的相对误差主要集中在0%～30%.前者仿真结果表明基于弹性BP神经网络的预测模型预测亚硝酸盐浓度是可行的；后者仿真结果表明，通过改进的自适应遗传算法获取弹性BP神经网络的预测模型的初始权值与阈值，预测时间缩短.

[1]王洪亮，高杨，程同蕾，等.营养盐传感器在海洋监测中的研究进展[J].山东科学，2011，24（3）：32-36.

[2]李鸿妹，石晓勇，陈鹏，等.春季东海赤潮发生前后营养盐及溶解氧的平面分布特征[J].环境科学，2013，34（6）：2159-2165.

[3]KAZEMZADEH A，ALI A Ensafi.Sequeential flow injection spectrophotometric determination of nitrite and nitate in various smaple[J].Analytica Chimica Acta，2001，442（2）：319-326.

[4] 王亚林，高锦章.甲基紫用作光度法测定亚硝酸根[J].分析化学，1998，26（11）：1384-1387.

[5]王智丽，韩永辉，杜振辉，等.海水营养盐自动分析系统的研究[J].现代仪器，2004（2）：32-34.

[6]王林，赵冬至，杨建洪.基于环境一号卫星的大洋河河口海域营养盐遥感反演 [J].中国环境科学，2012，32（1）：136-141.

[7]刘超.东海黑潮区营养盐月际变化及其影响因素研究[D].上海：上海师范大学，2012.

[8]赖廷和，韦蔓新.廉州湾五项营养盐变化与环境因子的关系[J].广西科学院学报，2003，19（1）：35-39.

[9]曲丽梅，姚德，丛丕福.辽东湾氮磷营养盐变化特征及潜在性富营养评价[J].环境科学，2006，27（2）：263-267.

[10]吴金浩，王年斌，张玉凤，等.夏季大连湾溶解氧分布变化特征及其与营养盐的关系[J].海洋通报，2013，32（1）：66-71.

[11]SANDFORD R C，EXENBERGER A，WORSFOLD P J.Nitrogen cycling in natural waters using in situ，reagentless UV spectrophotometry with simultaneous determination of nitrate and nitrite[J].Environmental Science&Technology，2007，41（24）：4045-4052.

[12]JOHNSON K S，NEEDOBA J A，RISER S C，et al.Chemical sensor networks for the aquatic environment[J].Chemical Reviews，2007，107（2）：623－640.

[13]米铁柱，于志刚，姚庆祯，等.春季莱州湾南部溶解态营养盐研究[J].海洋环境科学，2001，20（3）：14-18.

[14]阚文静，张秋丰，石海明，等.近年来渤海湾营养盐变化趋势研究[J].海洋环境科学，2010，29（2）：238-241.

[15]陈明.MATLAB神经网络原理与实例精解[M].北京：清华大学出版社，2013.

[16]王小平，曹立明.遗传算法——理论、应用与软件实现[M].西安：西安交通大学出版社，2000.

[17]陈明.MATLAB神经网络原理与实例精解[M].北京：清华大学出版社，2013.

Nitrite prediction model based on adaptive genetic algorithm and elastic BP neural network

LIN Zhi-gui1，2，3，YAO Fang-qin3，FENG Lin-qiang1，DU Jun-lan1，LI Jian-xiong3
（1.Laboratory of marine environment observation and monitoring technology of offshore，National Ocean Technology Center，Tianjin 300112，China；2.School of Precision Instrument&Opto-Electronics Engineering，Tianjin University，Tianjin 300072，China；3.School of Electronicsand Information Engineering，Tianjin Polytechnic University，Tianjin 300387，China）

Currently nutrients are detected by the chemical method.A chemical method cannot get online detection.To solve the problem，based on the relationship between nutrients and their impact factors，a prediction model which combined Adaptive Genetic Algorithm and Elastic BP Neural Network is put forward in this paper.Using the improved Adaptive Genetic Algorithm，the initial weights and thresholds of Elastic BP Neural Network are obtained by the crossover and mutation to accelerate the prediction process.The imporoved model predicts the nitrite by using the data of its impact factors.Simulation results show that it is feasible to predict the nutrient concentration by using the prediction model based on the Elastic BP Neural Network.The relative error of nitrite concentration value mainly focuses on 0-30%.The prediction model based on Adaptive Genetic Algorithm and Elastic BP neural network is better than that based on Elastic BP Neural Network.

nitrite；prediction；adaptive genetic algorithm（AGA）；elastic BP neural network

TP391

A

1671－024X（2015）03－0067－06

10.3969/j.issn.1671-024x.2015.03.015

2014-12-18

国家自然科学基金项目资助（61372011）

林志贵（1974—），男，博士，副教授，研究方向为环境信息处理及应用.E-Mail：linzhigui@tjpu.edu.cn