基于方差的优良粒子群多约束路由选择算法
马 刚
(福建师范大学闽南科技学院计算机系,福建泉州 362332)
通过使用电脑、手机等终端以实现计算机网络通信,已经成为了大众必不可少的生活方式之一,为了使通信业务网提供高质量的信号传输服务,在电路创建、连接、调度、释放时需要遵循一定的管理原则,运营商在路由选择中需要考虑如下的因素〔1〕:
(1)同类互斥原则:同类型同向电路尽量选择不同的路径;
(2)可靠性原则:路由选择应考虑网络链路的可靠性;
(3)负荷分担原则:开通的电路应在不同传输系统之间进行负荷分担;
(4)最少转接次数原则:电路路由应尽可能减少在不同传输系统间的转接。
我们把以上原则转换为另外一种用于描述最优路由路径选择的网络理论概念,就是指使用现有的有效资源为用户、应用需求提供新请求的最佳实时路由〔2-3〕。多约束路由选择是一个NP完全问题,虽然已有部分学者提出了逼近算法,但是至今还没有被彻底解决。国内外许多研究人员提出了若干个智能算法,想找出一个算法来解决网络路由选择问题,通过研究发现,一种叫做基于粒子群优化算法的路由选择算法,取得了比较好的通信效果。
这种新兴的智能算法——粒子群优化算法(Particle Swarm Optimization,PSO)是在 1995年由Eberhart和Kennedy提出的模拟鸟群集体协作而共同飞行觅食(目标)的行为算法〔4-5〕。该算法是一种概念简明,实现方便,参数设置较少的多约束目标搜索算法,在简单的约束条件下目标搜索较为精确,但是人们往往使用的是更新后的PSO算法,这种新的PSO算法已经广泛应用在工程领域中。本文就提出了基于传统粒子群算法之上,利用方差而得到的新粒子作为后继优良粒子,根据这些优良粒子搜索目标,获得最佳的路由。
1 问题描述
计算机网络的理论来源于图论及其集合,王树禾教授出版的《图论》教材〔6〕中把网络模型表示用赋权图G=(V,E)来描述,其中V是图中所有节点组成的集合,E是图中所有边的集合,每一条边表示相邻两节点间的直达通信路径,假定相邻两节点间最多仅有一条边。对于一个路由请求R,路由算法如果能够找到一条具有最小费用的路径L,同时满足条件:带宽限制,端到端时延限制,端到端费用限制。Bandwidth,Delay分别代表要求的带宽、时延。目标是找链路路径L,不仅满足所有约束条件,而且链路传输费用之和最小,即s.t.约束条件如下所示。
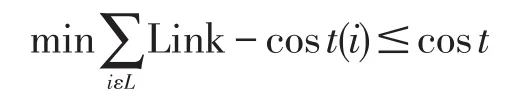
2 粒子群算法及算法更新
传统粒子群算法描述是:Van den Bergh通过时粒子群中最佳粒子始终处于运动状态,得到保证收敛到局部最优的改进算法,但其性能并不佳〔7〕。Kennedy等研究粒子群的拓扑结构,分析粒子间的信息流,提出了一系列的拓扑结构〔8-10〕。Angeline将选择算子引入到PSO中,选择每次迭代后的较好的粒子并复制到下一代,以保证每次迭代的粒子群都具有较好的性能〔6〕。传统的粒子群算法描述公式如下:Vk+1=wVk+c1r1(Pidk-Xk)+c2r2(Pgdk-Xk);Xk+1=Vk+1+Vk+1;其中,w为惯性权重;r1和r2为分布于[0,1]之间的随机数;k是当前迭代次数;Pid为个体最优粒子位置;Pgd为全局最优粒子位置;c1和c2为常数;V为粒子速度;X为粒子位置。
为了让粒子群算法具有很强的发现较好解的能力,不易陷入局部最优,综合其改进模式如下:
(1)算法的具体参数设定和调整策略:如Shi和Eberhart在速度项添加的惯性权重,后来提出的模糊自适应调整惯性权重思想。
(2)修改了算法的总体结构:适应粒子之间的信息交换,进一步影响了算法的寻优能力。
(3)混合算法:粒子群算法和其他算法结合。
为了挑选更优的下一代粒子,利用高等数学方差来从下一代粒子群中获取优越的粒子。首先统计系统中所有路由的总路径数和总费用,进而获取路由的平均费用f。利用这个平均费用值作为参的粒子作为优越的粒子(e值是很小的数)。考值,从新生成的下一代粒子群体中,把符合公式
3 基于数学方差的粒子群优化算法设计
在本研究解决的问题中,定义网络中两个节点间存在通路作为自我;否则,即为非自我。根据优化设计思想,具体算法设计为:
(1)输入请求。输入路由请求的各项参数R。
综上所述,使用乳房按摩能够促进足月孕产妇宫颈成熟与分娩,临床可以推荐使用该方法进行促进孕产妇宫颈成熟。
(2)根据路由请求信息,统计与此路由有关的总费用和总路径数,计算出平均费用f。
(3)产生初始抗体。随机产生一批初始抗体N。
(4)计算粒子适应度;
(5)更新下一代粒子群;
(6)利用公式|xi-f|=<e从下一代的粒子种群中选取更优良的粒子群;
(7)如满足结束条件,则输出结果;否则,转(4)。
4 仿真实验结果
本文设计的网络拓扑结构如图1所示。其中,每个顶点用< delay,loss,delay_change>表示,其中的元素分别代表节点时延、节点丢失率和节点时延变化;每条边用<cost,width,delay_change> 表示,其中的元素分别代表边的费用、带宽和链路时延。表1给出了网络拓扑的相关权值信息。

表1 节点与边的网络权值
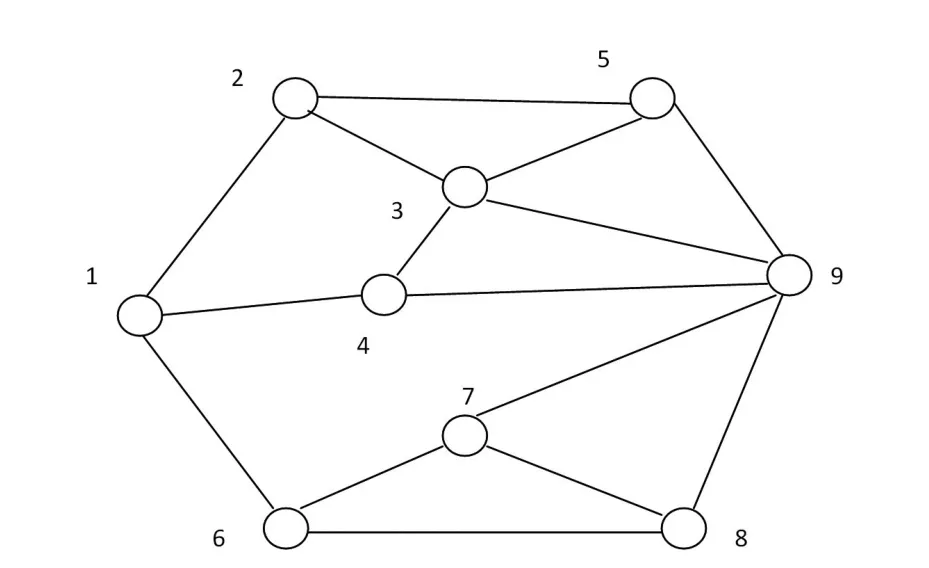
图1 网络拓扑结构
假设有3个路由请求 < 1,5>、< 1,9>、< 3、8>。通过仿真实验,表2给出了实验结果。
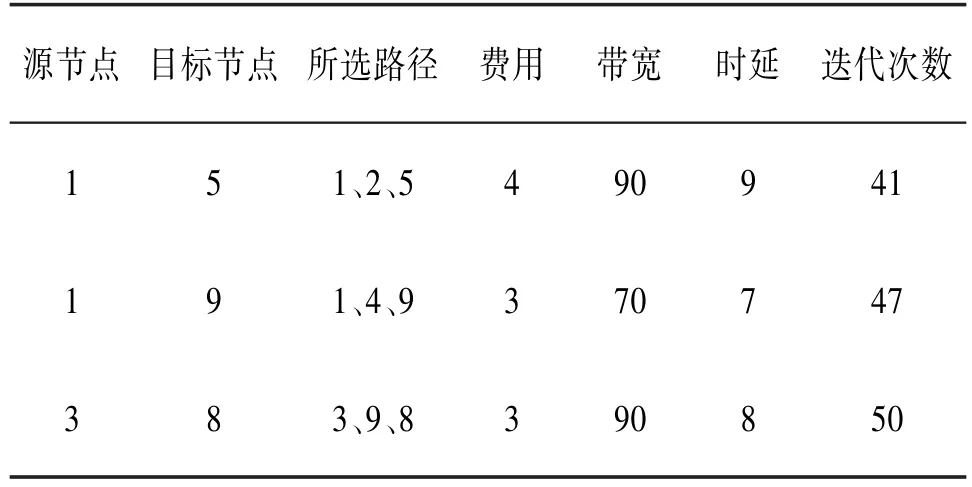
表2 实验结果
5 测试e值
为了确定e的值,本文首次提出了e的测量值计算方法,引入了基准测试函数。基准测试函数又常常称之为Benchmark函数,目前被经常使用的函数多达20个,含有多波谷峰函数、单峰函数、一维函数、高维次函数,它们分别代表着不同优化类型的工程问题,这些函数可以测试与衡量算法的性能,确定算法参数的合理区间值。下表列出了部分通用的基准函数。Sphere Model函数是基于对称结构的一种非线性化单峰数学函数,其全局最优值被认为是min(f1)=f1(0,0,0,0,...0,0,0)=0,其数学模型公式是f1(x)=∑Xi2,是一种具有比较好的测试智能目标优化算法的高精度寻优能力的函数。
e值测定的实验是在Matlab科学计算工具软件中执行的,在新引入的|xi-f|=<e条件下,更新了原来的基本粒子群优化算法PSO函数,在Matlab中对更新后的PSO优化算法提供了函数调用接口,指定了粒子数目N=50和迭代次数D=100次,惯性权值w=0.9,c1、c2因子各取值为1.3,在确保不影响获取优化结果值的要求下,对e值设置了3种阈值,实验结果如表3所示。
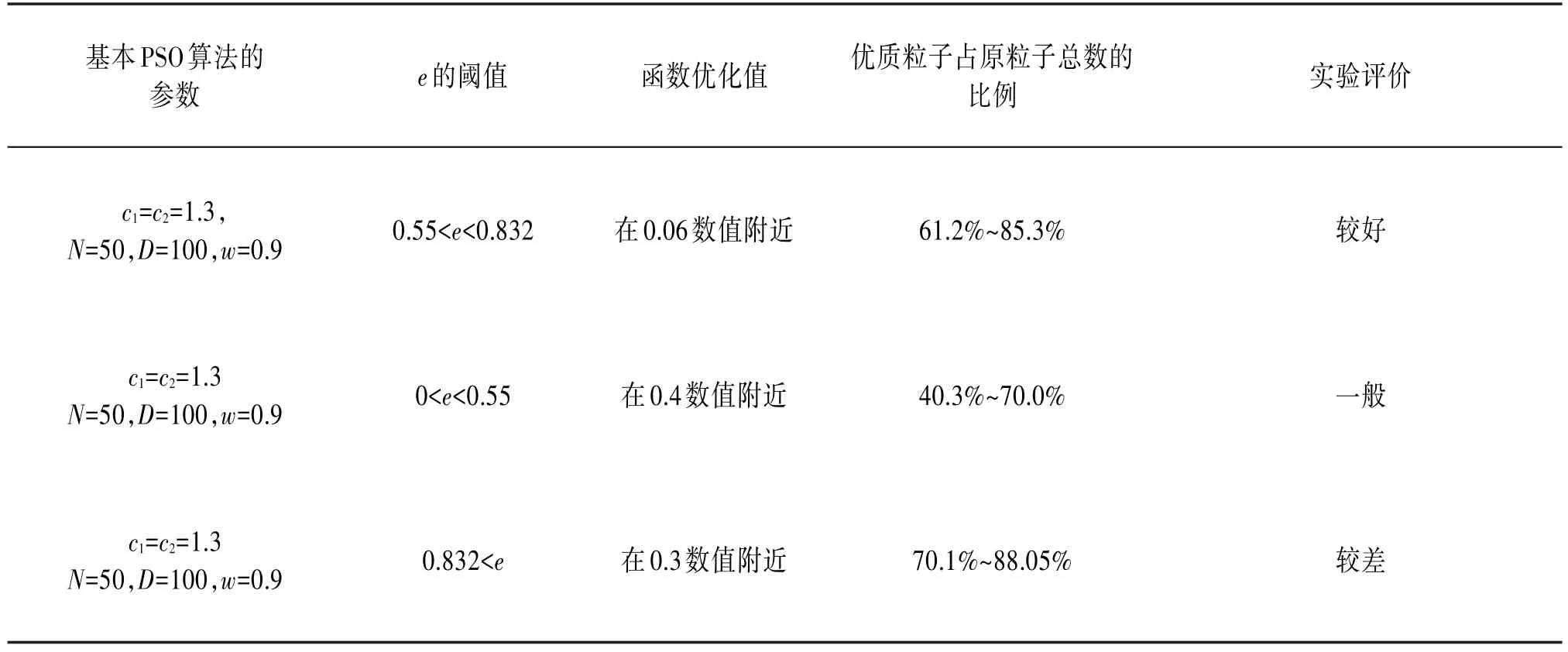
表3 实验统计e值
由表3中的实验结果可以分析出,e的阈值设定非常关键,当e在(0.55,0.832)区间时,优良的粒子占总数的比例比较小,算法的寻优结果也接近理论值。
6 结语
本研究中继续沿用了传统的粒子群粒子更新算法,并同时采用|xi-f|=<e继续对下一代粒子群进行选优,这样就减少了下一代粒子群的总数,减少了算法的复杂性,提高了算法的进化速度,对于e值的设定较为关键,还要进一步通过实验确定其值范围,来保证粒子群算法的全局寻优能力。
〔1〕熊翱.基于改进型蚁群系统的多约束电路路由算法〔J〕.计算机工程,2008,34(11):183-185.
〔2〕陈曦.基于免疫粒子群优化算法的多约束路由选择算法〔J〕.长沙交通学院学报,2006,22(2):56-59.
〔3〕熊翱.传送网网络质量评价模型和优化方法〔D〕.北京:北京邮电大学,2013.
〔4〕纪震,吴青华.粒子群算法及应用〔M〕.北京:科学出版社,2009:10-20.
〔5〕潘峰,李位星,高琪.动态多目标粒子群优化算法及其应用〔M〕.北京:北京理工大学出版社,2014:1-10.
〔6〕王树禾.图论〔M〕.北京:科学出版社,2009:10-20.
〔7〕刘波.粒子群优化算法及其工程应用〔M〕.北京:电子工业出版社,2009:13-25.
〔8〕VAN D B F.An analysis of particle swarm optimizer〔C〕//Proceedings of the 1998 conference of Evolutionary computation,Piscataway.IEEE Press,1998:67-73.
〔9〕MENDESR,KENNEDYJ.Thefullinformedparticleswarm:Simpler,maybe better〔J〕.IEEE Transaction on Evolutionary Computation,2004,8(3):204-210.
〔10〕ANGELINE P J.Using selection to improve particle swarm optimization〔C〕//Proceeding of the 1999 Congress on Evolutionary Computation,Piscatawar.IEEE Press,1999:84-89.

