考虑车架柔性的6×4商用车平顺性仿真*

金耿日 郭睿† 郑玲玲 管欣 郑灿赫

(1.吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130022； 2.吉林大学 机械科学与工程学院, 吉林 长春 130022)

考虑车架柔性的6×4商用车平顺性仿真*

金耿日1郭睿1†郑玲玲1管欣1郑灿赫2

(1.吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130022； 2.吉林大学 机械科学与工程学院, 吉林 长春 130022)

为了在初始设计阶段预测车辆平顺性、优化设计方案,建立考虑车架柔性的6×4商用车半车振动模型,进行随机输入行驶模拟试验,分析了车架弯曲、驾驶室悬置、发动机悬置及座椅悬置对整车平顺性的影响.利用假设模态方法建立车架弯曲模型,分析了车架柔性对整车平顺性的影响.通过灵敏度分析评价车辆主要参数对平顺性的影响,最后用模拟退火粒子群优化算法进行悬架和驾驶室悬置参数的优化匹配.仿真结果表明,前轴的悬架刚度和车架的第一阶弯曲振动对整车平顺性的影响很大,驾驶室悬置和座椅悬置对平顺性的贡献量最大.

汽车工程；商用车；平顺性；假设模态法；车架柔性

在初始设计阶段预测及优化车辆的动态性能是缩短开发周期、减少整车开发费用的重要环节.在这种无样车的概念设计阶段,用计算机仿真预测汽车性能及优化匹配其参数是现代汽车工业研究中的一个重要方法.

汽车行驶平顺性是影响驾驶员疲劳的重要特性.与乘用车相比,商用车在结构和运行方面具有很大不同.商用车驾驶员座椅的位置一般比乘用车的高得多,因此驾驶员俯仰角速度通常很大,这会导致驾驶员纵向加速度的增加.商用车的路面激励传递路径也跟乘用车不同.对于乘用车,路面激励一般通过轮胎和悬架传递至驾驶员,但对于商用车,路面激励先通过轮胎和悬架传递给车架,再通过驾驶室悬置和座椅悬置最终传给驾驶员.从运行方面考虑,商用车的运行时间一般比乘用车长,驾驶员的驾驶疲劳严重影响车辆的安全行驶,且商用车的交通事故往往会带来巨大的经济损失和环境破坏.为了改善商用车的平顺性,提高车辆的行驶安全性,徐中明等[1]研究了两轴商用车的15自由度模型,通过改进驾驶室悬置,使驾驶室的乘坐舒适性得到了改善.Demerdash等[2]研究了多轴军用车的平顺性,对比了两轴、三轴和四轴车辆的平顺性.王登峰等[3]以动力总成振动激励对驾驶员座椅地板垂直振动加速度的传递路径分析为例,分析并识别了对整车行驶平顺性影响较大的动力总成悬置的主要振动传递路径.

影响平顺性的部件较多,比如悬架、发动机悬置、驾驶室悬置与座椅悬置等.驾驶室悬置是与座椅悬置、发动机悬置、悬架等一起作用的,它们之间存在相互耦合作用,而且轴距和车架的弯曲也是影响平顺性的重要参数,所以,光考虑驾驶室悬置或者发动机悬置没有太大意义,同时考虑及优化影响平顺性的参数才是提高平顺性的最好方法.

到目前为止,对多轴重型商用车平顺性的研究尚不多见,尤其是综合考虑影响平顺性的子系统的研究则更为少见.有鉴于此,文中建立了考虑车架弯曲、发动机悬置、驾驶室悬置与座椅悬置的商用车振动模型,通过随机输入行驶模拟试验分析驾驶室悬置、发动机悬置和车架弯曲弹性振动等因素对平顺性的影响,通过灵敏度分析评价了车辆主要参数对整车平顺性的影响,并采用粒子群优化(PSO)算法优化了整车悬架和驾驶室悬置等对平顺性最敏感的子系统,以期为商用车整车平顺性的提高提供理论依据.

1 6×4商用车半车模型

1.1 半车振动模型

为了研究车架柔性对整车性能的影响,分别构建了9、10、11、12自由度的半车振动模型,确定了车架弯曲弹性振动阶次.9个自由度包括：座椅的垂向位移zs,驾驶室质心的垂向位移zc,驾驶室质心的俯仰角θc,发动机质心的垂向位移ze,车架的垂向位移zt,车架的俯仰角θt,3个车轴各自的垂向位移z1、z2、z3.10个、11个、12个自由度除了上述的9个自由度以外,还分别包括车架的1阶、2阶、3阶弯曲qt1,qt2,qt3,因此可以说9自由度模型是刚体模型,10、11、12自由度模型是刚体-柔体混合模型.图1所示为所建立的6×4商用车半车振动模型.

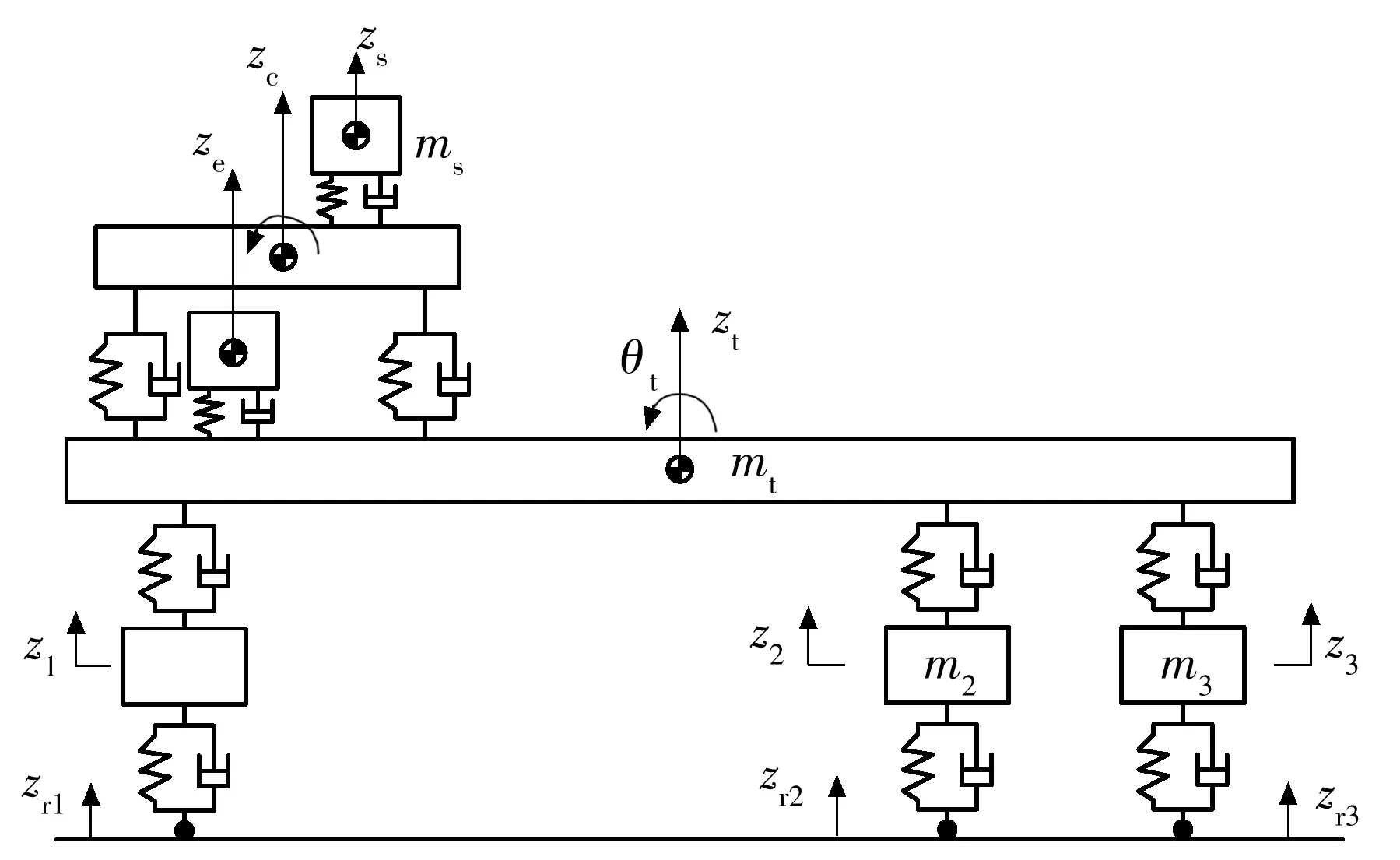
图1 6×4商用车半车振动模型

模型参数如下：座椅悬置的刚度ks和阻尼cs,座椅质量(包含驾驶员)ms；发动机悬置的刚度ke和阻尼ce,发动机质量me；驾驶室前悬置的刚度kcf和阻尼ccf,驾驶室后悬置的刚度kcr和阻尼ccr,驾驶室质量mc,从驾驶室质心到前悬置的距离n,从驾驶室质心到后悬置的距离p；从车架质心到驾驶员座椅、驾驶室质心及发动机质心的距离d、e、f,车架质量mt；轴1非簧载质量m1,轴1悬架刚度k1和阻尼c1,轴1轮胎刚度kt1和阻尼ct1,轴1轮胎下地面激励位移zr1,从车架质心到轴1的距离a,从车架质心到车架前端的距离l；轴2非簧载质量m2,轴2悬架刚度k2和阻尼c2,轴2轮胎刚度kt2和阻尼ct2,轴2轮胎下地面激励位移zr2,从车架质心到轴2的距离b；轴3非簧载质量m3,轴3悬架刚度k3和阻尼c3,轴3轮胎刚度kt3和阻尼ct3,轴3轮胎下地面激励位移zr3,从车架质心到轴3的距离c,从车架质心到车架后端的距离m.

1.2 车架的弯曲

车架的弯曲影响汽车平顺性和操纵稳定性[4- 5].Ibrahim等[6]通过有限元方法计算出了车架的模态质量、刚度和阻尼,并用模态叠加法建立了车架柔性模型,通过比较刚体模型和柔体模型,发现车架柔性对驾驶员垂向加速度和驾驶室俯仰加速度的影响很大.文中将车架视为等载面梁,可列出欧拉-白努利梁的运动微分方程式[7]：

(1)

式中：E为弹性模量,I为转动惯量,ρ为梁的密度,A为载面积,η为梁的垂直位移,x为梁的水平方向坐标, f(*)为外力,t为时间.无阻尼自由振动时,

f(x,t)=0

(2)

利用分离变量法,

η(x,t)=X(x)T(t)

(3)

式中,

X(x)=C1cos(βx)+C2sin(βx)+ C3cosh(βx)+C4sinh(βx).

则自由两端的边界条件如下：

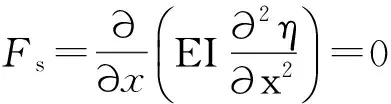
因此,

X(x)=C2[sin(βx)+sinh(βx)+

(4)

或者

(5)

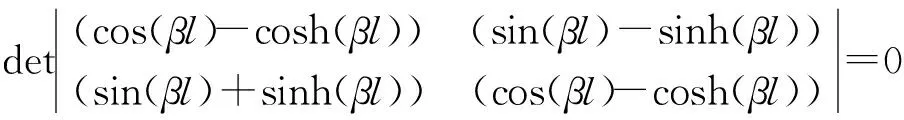
故有

cos(βl)cosh(βl)=1

(6)

以上各式中,C1、C2、C3、C4为取决于边界条件的常数,β为与梁的形式和振型有关的常数,l为梁的长度.

式(6)有无限个解,每个解都与梁的振型一一对应,第一个解与梁的刚体运动对应,如表1所示.

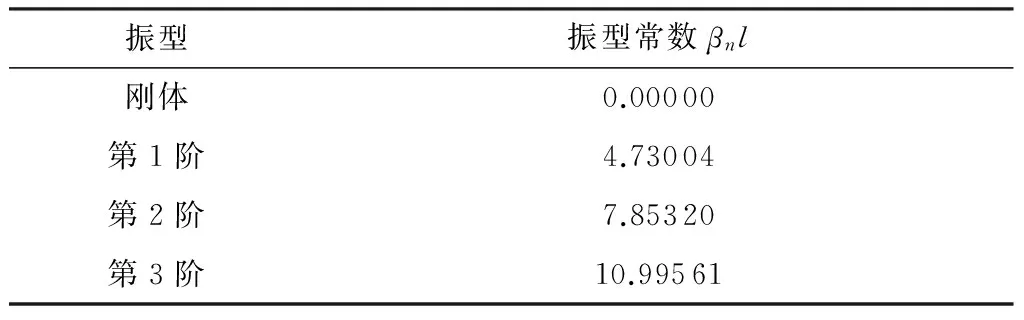
表1 两端自由梁的振型常数

用拉格朗日方法建立车架弯曲模型,利用假设模态方法设梁的位移表现为有限级数,即

(7)

式中,fti(x)为梁的第i个振型函数,qti(t)为第i个广义模态坐标.

如果已经知道梁的固有频率,那么车架的抗弯曲刚度可以表示如下：

(8)

式中, fn为梁的n阶固有频率,βn为与梁的形式和n阶振型有关的常数,ρA为车架的单位长度质量.

1.3 运动方程的矩阵形式

6×4商用车的半车振动模型用拉格朗日方法推导[7].拉格朗日方法利用了系统的动能T*和势能V.系统的拉格朗日函数为

L=T*-V

(9)

(10)

根据哈密顿原理,拉格朗日方程为

(11)

式中,Qj为广义非保守力.

这里以车架为例说明车辆模型的推导过程.10自由度模型里车架的独立广义坐标如下：

ξj=[ztθtqt1].

广义非保守力为零,即Qj=0.

车架的动能和势能分别为

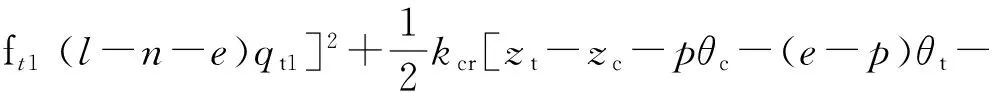
cθt-ft1(l+c)qt1]2.

车架的弯曲刚度为

式中, fc为车架的固有频率.

从上式可以知道,ρA决定车架的弯曲刚度,是一个反映车架柔性的指标.可以通过拉格朗日方程推导车架子系统的运动方程如下：

(12)

从上式可以推导车架的垂向运动方程、俯仰运动方程和一阶弯曲运动方程.最终6×4商用车的半车振动方程矩阵形式可描述如下：

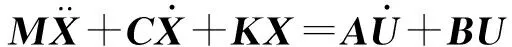
(13)

式中:M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；A为路面输入阻尼矩阵；B为路面输入刚度矩阵；X为系统的未知矢量；U为路面不平度垂向位移矢量,U=[zr1zr2zr3]T.

质量矩阵、阻尼矩阵和刚度矩阵都是对称矩阵.9、10、11、12自由度模型的未知矢量分别如下：

9自由度模型,

X=[zszcθczeztθtz1z2z3]T；

10自由度模型,

X=[zszcθczeztθtqt1z1z2z3]T；

11自由度模型,X=[zszcθczeztθtqt1qt2z1z2z3]T；

12自由度模型,X=[zszcθczeztθtqt1qt2qt3z1z2z3]T.

2 车辆平顺性的影响因素分析

影响整车平顺性的因素很多,比如悬架的刚度和阻尼、驾驶室悬置、座椅等.很多学者已研究了悬架特性对整车性能的影响[8- 9],因此文中不再重复,这里主要研究车架弯曲、发动机悬置、驾驶室悬置和座椅悬置等的影响.

2.1 车架弯曲振动频率的影响

与乘用车不同,重型商用车车架的弯曲振动对平顺性的影响不可忽略[10].文中以某款6×4平头载货卡车为例,用Matlab进行了仿真.该车辆车架的低阶垂向弯曲振动固有频率分别为11.7、32.4和105.0 Hz.用文中模型进行了随机输入行驶模拟试验[9,11].

一种被普遍接受的随机路面功率谱拟合表达式如下：

(14)

式中:Gq(ω)为路面垂直位移不平度功率谱密度,简称路面功率谱密度(m2/m-1);ω为空间频率,是波长的倒数,表示每米长度包含的波数(m-1)；ω0为参考空间频率,ω0=0.1 m-1；Gq(ω0)为参考空间频率ω0下的路面功率谱密度,又称路面不平度系数(m2/m-1)；w为频率指数,是双对数谱密度曲线的斜率,它决定着路面功率谱密度的频率结构.

在B级路面上分别用9、10、11和12自由度模型进行了随机输入行驶模拟试验,驾驶员座椅处的加权加速度均方根[12]如表2所示.可以看出,车架弯曲振动的影响占10%左右,不可忽略.而考虑1阶、2阶振动(低频范围)能够满足计算精度.

一般重型卡车和半挂车的车架柔性较大,其第一阶弯曲频率在10 Hz左右.与乘用车相比,重型商用车的俯仰振动引起的驾驶员纵向加速度一般比垂

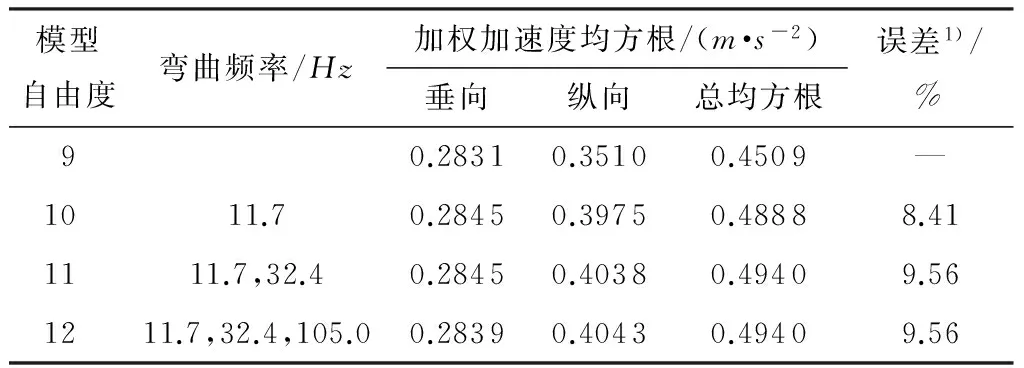
表2 座椅处的加权加速度均方根

1)指相对刚体模型的误差,下同.

向加速度大.

表3所示为车架弯曲振动频率对整车平顺性的影响.考虑车架柔性时,座椅处的加权加速度均方根比刚体模型大,加速度随着车架弯曲振动频率的变化而变化,所以准确确定车架的弯曲频率是非常重要的.计算结果说明,车架弯曲频率较低时平顺性较差,也就是说,车架刚度较低时平顺性较差.对平顺性影响较大的车架弯曲频率范围应为低频范围.

表3 车架弯曲振动频率对平顺性的影响

Table3Influenceofframebendingvibrationfrequencyonridecomfort

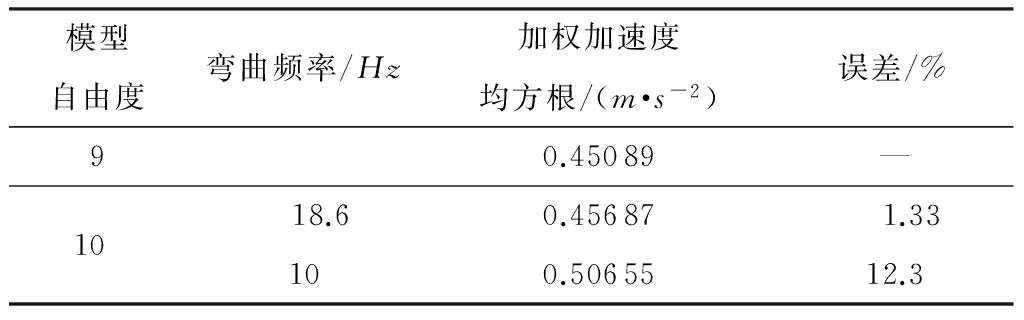
模型自由度弯曲频率/Hz加权加速度均方根/(m·s-2)误差/%90.45089—10 18.6100.456870.50655 1.3312.3

2.2 发动机悬置的影响

发动机悬置是隔离发动机振动及影响汽车平顺性的重要元件[13].表4是用9自由度模型(全浮式驾驶室)计算得到的发动机悬置和非悬置情况下的座椅处加权加速度均方根.

表4 发动机悬置对平顺性的影响

从表4可以看出,采用发动机悬置比不采用悬置可减少5%左右的驾驶员座椅处加速度.发动机悬置会起到一定的减振作用,其贡献量随着行驶速度的增加而提高,通过恰当选择发动机悬置,可以改善整车的动力学性能.

2.3 座椅悬置的影响

作为驾驶员和驾驶室之间的连接体,座椅不仅仅支撑驾驶员体重,还隔离来自路面和发动机的振动和冲击[14- 15],所以在改善平顺性方面也起着重要作用.表5是用9自由度模型(全浮式驾驶室)计算得到的座椅悬置和非悬置情况下的座椅处加权加速度均方根.

表5 座椅悬置对平顺性的影响

从表5可以看出,采用座椅悬置可以将汽车平顺性提高20%左右.

2.4 驾驶室悬置的影响

驾驶室悬置是改善重型商用车平顺性时第一选择的重要调教环节[16].表6是用9自由度模型计算得到的驾驶室悬置情况下的座椅处加权加速度均方根.从表6可以看出,用全浮式驾驶室悬置时减震效果最好,但成本高,结构相对复杂.

表6 驾驶室悬置形式对平顺性的影响

综上可知,对商用车来说,驾驶室悬置对驾驶员座椅处加速度的影响很大.

3 灵敏度分析

用12自由度模型在随机输入的情况下进行了灵敏度分析,车辆速度设为70km/h.灵敏度分析的目的在于确定每个参数对汽车平顺性的影响,并为以后因改善车辆平顺性而修改设计时提供科学依据.灵敏度定义为随输入变化的输出变化率.灵敏度分析方法包括数值方法和分析法,文中采用数值方法.为了进行灵敏度分析,利用如下误差函数[17]：

(15)

式中,RMS(var)为灵敏度分析中每个参数变化时的驾驶员座椅处加速度均方根,RMS(base)为每个参数设定为初始值时的驾驶员座椅处加速度均方根.灵敏度分析中，每个参数的变化范围为初始值的±10%、±20%、±30%、±40%、±50%.灵敏度分析中使用的变量见表7.

表7 灵敏度分析变量表

灵敏度分析结果如表8所示.可以看出,对驾驶员的加速度影响最大的是轴1的悬架刚度,其次是车架的第1阶弯曲频率.当然,对每个车型,其结果有所不同,这里只是提供参考.

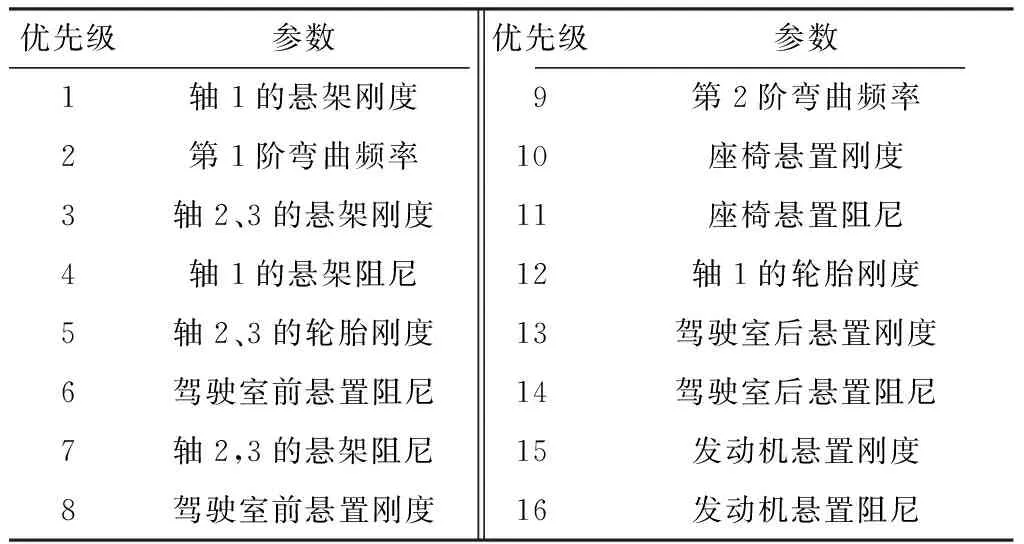
表8 参数的灵敏度优先级

4 基于悬架参数匹配的平顺性优化

充分考虑驾驶室悬置系统与主悬架系统参数的匹配所达到的隔振效果要好于单独改进驾驶室悬置系统参数的效果,因此,在进行整车设计时应综合考虑底盘主悬架系统与驾驶室悬置系统.优化改进必须在现有设计的基础上进行,且尽可能使原有设计改动最小.从灵敏度分析结果可知,整车平顺性对悬架和驾驶室悬置参数的变化最敏感,所以仅改进这些参数即能达到改善平顺性的效果.这里以8个悬架、驾驶室悬置参数为设计变量,以驾驶员座椅加速度、悬架动行程和轮胎动载荷为优化目标,进行了参数优化匹配.优化过程中,车辆行驶速度为80km/h.粒子群优化算法是近年来发展起来的一种新的进化算法[18].模拟退火算法在搜索过程中具有概率突跳的能力,能够有效避免搜索过程中陷入局部极小解,它在退火过程中不但接受好的解,还以一定的概率接受差的解,同时这种概率受到温度参数的控制,随着温度的下降而减小.文中采用模拟退火粒子群优化算法进行优化.其适应度函数设定为

(16)

式中,armsc、F1c、F2c、F3c、D1c、D2c和D3c分别为优化前驾驶员座椅处的加权加速度均方根、轴1轮胎动载荷、轴2轮胎动载荷、轴3轮胎动载荷、轴1悬架动行程、轴2悬架动行程和轴3悬架动行程,arms、F1、F2、F3、D1、D2和D3分别为优化后驾驶员座椅处的加权加速度均方根、轴1轮胎动载荷、轴2轮胎动载荷、轴3轮胎动载荷、轴1悬架动行程、轴2悬架动行程和轴3悬架动行程,r1、r2、r3为加权系数.优化过程中假设驾驶员座椅处的加权加速度均方根、轮胎动载荷和悬架动行程具有同样的加权系数.根据不同的要求,可以调整加权系数,亦可将悬架动行程和轮胎动载荷作为约束函数进行优化.优化结果见表9和10.

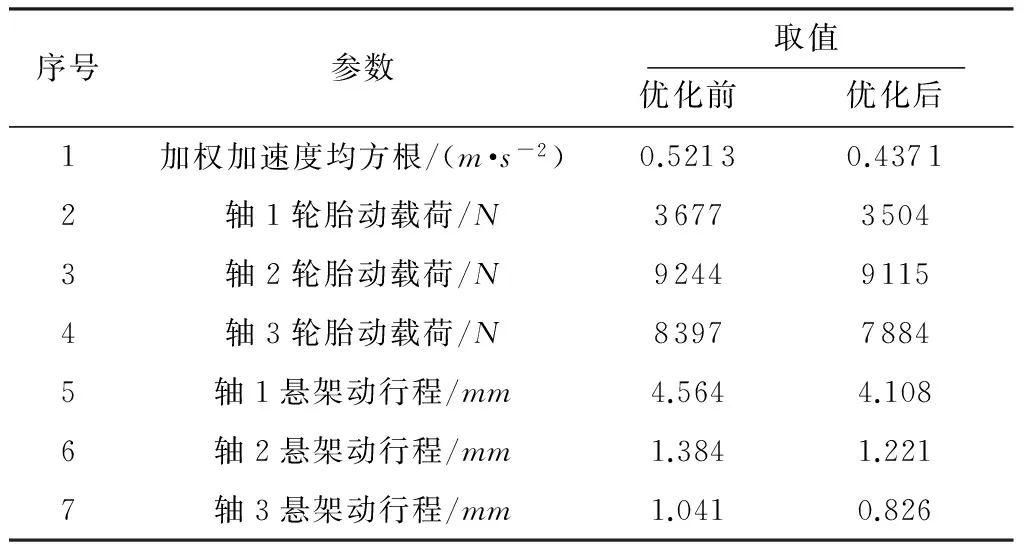
表9 悬架性能指标优化结果Table 9 Optimization results of performance indexes of suspension

表10 悬架参数优化结果

从上述结果可以看出,通过优化,驾驶员座椅处的加速度均方根减小了16.2%,其他悬架性能指标也优化了不少,说明在初始设计阶段通过悬架和驾驶室悬置等参数的优化匹配可以提高整车性能.

5 结语

文中建立了考虑车架弯曲的商用车振动模型,分析了车架弯曲、驾驶室悬置、发动机悬置及座椅悬置对汽车平顺性的影响.结果表明,考虑车架柔性时,准确确定车架的弯曲振动频率具有重要意义.从改善平顺性的角度来考虑,驾驶室悬置和座椅悬置的贡献最大,发动机悬置也起到一定的减震作用.按照文中提出的模型进行了灵敏度分析,发现对驾驶员座椅处加速度最敏感的参数是前轴的刚度和车架第1阶弯曲频率.文中还用模拟退火粒子群优化算法进行了悬架参数和驾驶室悬置参数的优化匹配,结果表明通过优化可在预设计阶段提高整车性能.

在汽车预开发阶段,应用文中提出的模型可以预测及评价其平顺性,缩减研发周期.进一步研究商用车及柔性车架的建模对提高商用车性能具有重要意义.

[1] 徐中明,张志飞,贺岩松.15自由度重型汽车乘坐舒适性计算机仿真 [J].计算机仿真,2005,22(2):195- 198,214. Xu Zhong-ming,Zhang Zhi-fei,He Yan-song.Computer simulation of 15DOFs model for heavy-duty vehicle [J].Computer Simulation,2005,22(2):195- 198,214.

[2] Demerdash S M El,Rabeih E M A.Ride performance analysis of multi-axle combat vehicles,SAE paper,2004- 01- 2079 [R].[S.l.]:SAE International,2004.

[3] 王登峰,李未,陈书明,等.动力总成振动对整车行驶平顺性的传递路径分析 [J].吉林大学学报:工学版,2011,41(2):92- 97. Wang Deng-feng,Li Wei,Chen Shu-ming,et al.Transfer path analysis of power train vibration on vehicle ride comfort [J].Journal of Jilin University:Engineering and Technology Edition,2011,41(2):92- 97.

[4] 王登峰,郝赫,刘盛强,等.车架弹性对重型载货汽车行驶平顺性的影响 [J].农业机械学报,2010,41(12):7- 12. Wang Deng-feng,Hao He,Liu Sheng-qiang,et al.Frame flexibility’s effect on ride comfort of heavy-duty truck [J].Transactions of the Chinese Society for Agricultural Machinery,2010,41(12):7- 12.

[5] Warwas Kornel,Adamiec-Wojcik Iwona.Modelling articulated vehicles with a flexible semi-trailer [J].Archive of Mechanical Engineering,2013,60(3):389- 407.

[6] Ibrahim I M,Crolla D A,Barton D C.Effect of frame flexibility on the ride vibration of trucks [J].Computers & Structures,1996,58(4):709- 713.

[7] Meirovitch Leonard.Fundamentals of vibrations [M].New York:McGraw-Hill,2001.

[8] 余志生.汽车理论 [M].5版.北京:机械工业出版社,2009.

[9] Wong J Y.Theory of ground vehicles [M].New York:John Wiley & Sons,2001.

[10] Geoff Rideout D.Simulating coupled longitudinal,pitch and bounce dynamics of trucks with flexible frames [J].Mo-dern Mechanical Engineering,2012,2(4):176- 189.

[11] GB/T 4970—2009,汽车平顺性试验方法 [S].

[12] ISO-2631-1,Mechanical vibration and shock evaluation of human exposure to whole-body vibration(part 1):general requirements [S].

[13] 运伟国,王邵斌,杨少华.重型汽车动力总成悬置NVH性能研究 [J].噪声与振动控制,2014,34(5):99- 101,149. Yun Wei-guo,Wang Shao-bin,Yang Shao-hua.NVH performance study of a heavy-duty truck’s powertrain mount [J].Noise and Vibration Control,2014,34(5):99- 101,149.

[14] Sun Weichao,Li Jinfu,Zhao Ye,et al.Vibration control for active seat suspension systems via dynamic output feedback with limited frequency characteristic [J].Mechatronics,2011,21(1):250- 260.

[15] Shimogo T,Oshinoya Y,Shinjyo H.Active suspension of truck seat [J].Transactions of the Japan Society of Mechanical Engineers C,1996,62(1):3132- 3138.

[16] Tiemessen Ivo J,Hulshof Carel T J,Frings-Dresen Monique H W.An overview of strategies to reduce whole-body vibration exposure on drivers:a systematic review [J].International Journal of Industrial Ergonomics,2007,37(3):245- 256.

[17] Atkinson KE,Han W.Elementary numerical analysis [M].New York:John Wiley & Sons,2004.

[18] Clerc M,Kennedy J.The particle swarm-explosion,stability and convergence in a multidimensional complex space [J].IEEE Transactions on Evolutionary Computation,2002,6(1):58- 73.

Simulation of Ride Comfort of 6×4 Commercial Vehicles in the Consideration of Frame Flexibility

KimKyongil1GuoRui1ZhengLing-ling1GuanHsin1JongChanhyok2

(1.State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,Jilin,China;2.College of Mechanical Science and Engineering,Jilin University,Changchun 130022,Jilin,China)

In order to predict the ride comfort and optimize the design scheme during the initial design stage,a half car vibration model of 6×4 commercial vehicles is constructed by taking into account the frame flexibility,and random input running tests are simulated.Next,the influences of vehicle suspension,cab suspension,engine mount and seat suspension on the ride comfort are analyzed.Then,a frame bending model is constructed by means of the assumed mode method,and the influence of the frame flexibility on the ride comfort of a whole vehicle is revealed.Furthermore,the influence of main vehicle parameters on the ride comfort is also evaluated through sensitivity analysis.Finally,the optimal matching of primary suspension and secondary one is processed by using the particle swarm optimization (PSO) algorithm.Simulation results show that both the stiffness of the first axle suspension and the first bending vibration of frame greatly affect the ride comfort,and the cab suspension and the seat suspension contribute most to the ride comfort.

automotive engineering;commercial vehicle;ride comfort;assumed mode method;frame flexibility

2015- 02- 11

教育部长江学者和创新团队发展计划项目(IRT0626) Foundation item: Supported by the Program for Changjiang Scholars and Innovative Research Team in University of Ministry of Education of China(IRT0626)

金耿日(1979-),男,博士生,主要从事车辆系统动力学与控制研究.E-mail: kimkyongil@163.com

† 通信作者： 郭睿(1978-),女,讲师,主要从事车辆系统动力学及车辆动态模拟仿真研究.E-mail: guor@jlu.edu.cn

1000- 565X(2011)11- 0105- 07

U 461.4

10.3969/j.issn.1000-565X.2015.11.015