混杂纤维增强RPC加固混凝土梁抗弯性能

邓宗才，张戊晨

(北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)

混杂纤维增强RPC加固混凝土梁抗弯性能

邓宗才，张戊晨

(北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)

为了研究混杂纤维增强活性粉末混凝土(HFRPC)的加固效果,进行了高强钢筋HFRPC加固普通钢筋混凝土梁抗弯性能的试验和理论研究，并与未加固梁比较。共完成7根梁抗弯试验，其中1根是未加固梁，6根为HFRPC加固梁。变化参数为：HFRPC厚度、HFRPC与旧混凝土界面粘结方式和粘贴纤维布等。试验结果表明：采用高强钢筋HFRPC加固梁能有效提高抗弯承载力，HFRPC加固层与旧混凝土粘结牢靠，未发生脱粘破坏；HFRPC加固层裂缝数量众多、宽度明显减小；旧混凝土表面经凿坑处理比凿沟处理的加固梁承载力更大；HFRPC中配置高强钢筋，能发挥高强钢筋优势；HFRPC加固层厚度40 mm比30 mm梁抗弯承载力提高5%；采用纤维布箍约束新旧混凝土，可阻止弯曲裂缝扩展，峰值荷载后承载力下降较慢。最后，给出了加固梁开裂荷载、屈服荷载和极限承载力计算公式，计算值与试验结果吻合较好。

活性粉末混凝土；超高性能混凝土；混杂纤维；加固；增大截面法；抗弯性能；钢筋混凝土

目前，既有混凝土结构的加固维护已成为土木工程界关注的重要问题之一，相应的加固材料发展较快，加固方法较多，常用的加固方法有：增大截面、纤维增强复合材料(FRP)加固、粘钢板加固等。增大截面加固方法简便，在结构加固中应用最多，但若采用普通混凝土加固，混凝土容易开裂，影响结构耐久性，也不利于普通混凝土与既有混凝土之间的粘结。FRP加固法存在FRP与既有混凝土表面粘结易出现空鼓、粘结不牢靠的问题，且FRP与混凝土之间热交换性差，抗灾能力不足[1]。粘钢加固法存在对既有混凝土表面平整度要求高、钢板易锈蚀等问题。

采用活性粉末混凝土(reactive powder concrete, RPC)超高韧性混凝土加固既有结构，不但与旧混凝土相容性好，可提高新旧混凝土间粘结性能，而且可最大限度的利用这些高性能水泥基复合材料的控裂功能，降低裂缝扩展，有效弥补既有混凝土结构开裂造成的耐久性退化等问题[2-3]。钢纤维可以改善活性粉末混凝土变形性能，但钢纤维体积掺率在2%以内时，其弯曲韧性仍然不够理想。为了进一步改善其韧性，将钢纤维与高性能粗合成纤维混杂，优势互补，以改善其裂缝控制能力和韧性。混杂纤维活性粉末能混凝土(hybrid fiber reinforced reactive powder concrete，HFRPC)不但控裂能力强，且强度高，为高强钢筋的应用提供了条件，高强钢筋HFRPC有利于提高既有结构承载力和耐久性等。目前关于高强钢筋HFRPC加固既有混凝土梁抗弯性能的研究甚少。本文研究了高强钢筋HFRPC加固混凝土梁的抗弯性能，探讨了HFRPC加固层厚度、新旧混凝土界面处理方式等对加固效果的影响规律，研究成果将对高强钢筋HFRPC在加固领域中的应用提供参考。

1 试验概况

1.1 试验材料

原构件采用C40普通混凝土浇筑，其质量配合比为水泥∶水∶砂子∶石子=411.4∶195 ∶609.82 ∶1 183.78，水泥为PO42.5普通水泥。

加固用混杂纤维活性粉末混凝土配合比见表1。其中超细水泥为PO52.5硅酸盐水泥，比表面积约600 m2/kg；S95级粒化高炉矿渣粉，比表面积为408 m2/kg；石英砂粒径范围为40-70目；钢纤维为长度8 mm、直径0.12 mm微细钢纤维，抗拉强度大于2 800 MPa；粗聚烯烃纤维长度38 mm、直径1 mm，抗拉强度600 MPa；高效聚羧酸减水剂，白色自乳化消泡剂。HFRPC采用强制式搅拌机搅拌。

原构件纵筋采用HRB335级钢筋，直径为10 mm和12 mm；箍筋为HRB335级钢筋，直径为8 mm。加固层钢筋为HRB500级钢筋，直径为8 mm。

表1 HFRPC配合比

1.2 试验梁设计

共设计7根梁，其中1根为未加固的钢筋混凝土梁，其截面尺寸为120 mm×150 mm，长1 200 mm，梁底纵筋为HRB300，配筋率为1.5%。保护层厚度为20 mm，截面尺寸和配筋见图1(a)；其余6根梁均采用配筋HFRPC进行抗弯加固，梁底HFRPC加固层均配有2根直径8 mm的HRB500钢筋。被加固梁的截面尺寸和配筋均同于未加固梁，加固后梁截面尺寸及配筋如图1(b)所示。

(a) 未加固梁N1

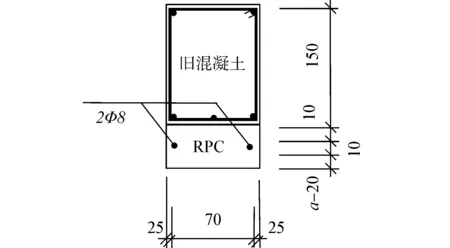
(b) 加固梁图1 试验梁截面配筋图Fig. 1 Test beam reinforcement plans

被加固梁浇筑7 d后进行加固。梁底HFRPC加固层厚度分别为30 mm和40 mm。HFRPC与原有混凝土界面有3种处理方式：A-凿坑处理，深度为15 mm，采用梅花形布置；B-钢丝刷刷毛处理；C-凿沟处理，深度为15 mm，间距150 mm。3种表面处理方式完成后，均涂刷一层界面粘结剂，以改善新旧混凝土之间的粘结性能。为了防止新加固的HFRPC与原混凝土之间发生界面粘结破坏，对刷毛处理的2根梁在加载点附近用玄武岩纤维布缠绕加强，纤维布宽度为250 mm，双层缠绕。

在浇筑梁时，同时浇筑了150 mm×150 mm×150 mm的普通混凝土立方体试块、100 mm×100 mm×100 mm的HFRPC立方体试块，用来测定抗压强度；HFRPC拉伸试件为100 mm×100 mm×400 mm的棱柱体。立方体和棱柱体试件养护方法同于梁，均采用天然养护方式。经试验测定，28 d普通混凝土抗压强度为42.4 MPa，HFRPC抗压强度为119.1 MPa；28 d HFRPC轴拉强度为5.6 MPa，开裂应变为0.000 156，极限拉应变为0.007。

表2 试验梁设计方案

试件编号、加固层厚度、截面处理方式等列于表2。试件编号的含义：N1为未加固梁，R为加固梁试件，第一个“-”后的数字为加固层厚度，最后的A、B、C表示3种界面处理方式及加固方式。

1.3 加载制度

为观察梁的纯弯曲性能，采用两点对称加载，跨中有350mm宽的纯弯段，如图2所示。加载仪器采用电液伺服控制系统，数据采集采用静态应变测试系统。

纵筋屈服前采用荷载控制模式，分级加载，在梁开裂前每级加载5kN，梁开裂后改为每级10kN加载。纵筋屈服后按位移控制模式加载，每级荷载稳定2～3min再开始下级加载。试验量测内容有：荷载、纯弯段纵筋应变、混凝土应变、跨中和支座处的位移、裂缝分布及宽度。

图2 试验梁加载示意图Fig. 2 Schematic diagram of the experimental beam loading

为验证梁在受弯过程中是否符合平截面假定，在梁跨中的侧面自上向下均匀粘贴5片应变片。在梁跨中顶部粘贴2片应变片，测量混凝土压应变。在梁跨中底部沿梁轴线方向粘贴3片应变片，测量梁底部混凝土拉应变。

2 试验结果与分析

2.1 破坏过程与破坏形态

未加固梁为适筋梁破坏形态。当荷载为17kN时，梁开裂；当荷载为51kN时，纵筋开始屈服；达到极限荷载时，受压区混凝土被压碎。梁破坏时，纯弯段弯曲裂缝条数较少，宽度明显大于加固梁。

6根加固梁均发生适筋破坏，未出现HFRPC加固层与原混凝土界面分离的现象。与未加固梁相比，加固梁底裂缝的数目明显增多，且缝宽变小。钢筋屈服时，加固梁底裂缝数目平均达到29条。梁底HFRPC层开裂后，裂缝缓慢向上扩展，当原混凝土梁底拉应变达到开裂应变时，原混凝土开裂；荷载增加，弯曲裂缝不断向上扩展，形成主裂缝。由于梁底HFRPC的控裂作用，梁裂缝扩展速率比未加固梁明显缓慢，梁最终破坏时，裂缝宽度较小。即HFRPC加固层对裂缝发展起到较好的抑制作用，使原本宽而少的裂缝转变为细而密的微细裂缝。

R-30-B和R-40-B两根梁，由于粘贴了纤维布，试验过程中无法观察纤维布下的裂缝情况。试验后，将纤维布去掉，观察混凝土表面，只发现很少的弯曲裂缝。与其他未包裹纤维布的HFRPC加固梁相比，纤维布下的混凝土表面裂缝数减少，且裂缝宽度很小。可见粘贴纤维布提高了梁抗裂性能，阻止了弯曲裂缝扩展，对改善梁抗弯性能有利。

2.2 荷载-挠度曲线

试验测得的荷载-跨中挠度曲线如图3所示。由图可见，加固梁经历了弹性变形、带裂缝工作阶段和屈服、破坏阶段。加固梁的初期刚度明显大于未加固梁，约为未加固梁的2倍。达到屈服荷载时，加固梁的跨中挠度稍大于未加固梁。用纤维布缠绕加固梁，无论加固厚度为30mm或40mm，当达到峰值荷载后承载力下降均较缓慢。

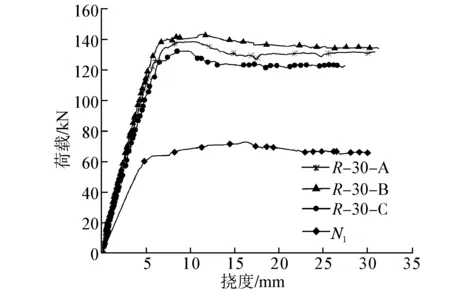
(a) 30 mm加固层试验梁

(b) 40 mm加固层试验梁图3 试验梁的荷载-挠度曲线Fig. 3 Load-deflection curves of beams

加载初期，加固梁荷载-挠度曲线为直线，梁底HFRPC开裂后，由于混杂纤维的阻裂效用，梁的刚度下降不明显，弯曲变形较小；跨中截面沿梁高度的应变为直线分布，符合平截面假定，受压区混凝土承受压应力，受拉区混凝土、HFRPC和钢筋共同承受拉应力。

这种多裂缝扩展模式不同于普通混凝土或自密实混凝土，普通混凝土裂缝少，但宽度大[4]。随着荷载的增大，受拉区原混凝土达到抗拉强度时开裂，并不断扩展，最终使受拉区大部分混凝土退出工作。由于梁开裂，抗弯刚度下降，在荷载-挠度曲线上出现了一个转折点，梁进入带裂缝工作阶段，受拉区主要依靠纵筋和HFRPC承受拉力，受压区混凝土应变不断增大，应变增长速度比应力增长速度快。

纵筋屈服后，梁进入第三阶段，梁挠度突然增大，主裂缝形成且沿梁高向上扩展，中和轴上移，受压区高度减小。当受压边缘混凝土达到极限压应变时，梁开始发生破坏。在第三阶段，钢筋的总拉力大致保持不变，但由于中和轴上移，内力臂稍有增大，极限荷载略大于屈服荷载。

2.3 混凝土应变沿高度分布

图4 R-30-A不同荷载下梁侧混凝土应变分布Fig. 4 Strain distribution of R-30-A concreate under different load levels

以梁R-30-A为例说明应变沿梁截面高度方向的分布规律，图4为该梁跨中截面在各级荷载下应变沿梁高分布情况。可见沿梁高方向混凝土及钢筋平均应变基本呈直线分布，符合平截面假定。

2.4 承载力、变形及主要影响因素

各梁的开裂荷载值、屈服荷载值和极限荷载值及对应的挠度值列于表3。可见加固梁的开裂荷载比未加固梁平均提高23.2%，屈服荷载提高约88.7%～114.4%，极限荷载提高约83.5%～105.7%。

2.4.1HFRPC厚度

依据美国通用会计准则，R&D中的“研究”是指发现有助于开发新技术或产品的调查或研究。“开发”是指将研究发现转变为新工艺或新产品，或利用其对现有工艺和产品进行重大改进的活动[2]。根据中国的《企业会计准则第六号—无形资产》规定，企业应区分研究阶段和开发阶段的支出，项目研发阶段的费用应当在发生时计入当期损益。

由表3知，梁底加固层厚度由30mm增大到40mm，加固梁承载力平均值从137kN增大到144kN，提高了5%。界面处理方式相同时，加固厚度由30mm增大到40mm，与屈服荷载、极限荷载对应的跨中挠度稍有减少，说明加固层厚度增大，梁的刚度增加，挠度减小。

表3 梁试验结果

2.4.2 界面处理方式

3种不同的界面处理方式中，凿坑处理和刷毛处理梁的极限承载力比凿沟处理梁高。其中凿坑处理梁的屈服荷载和极限荷载较高，抗弯刚度较大，挠度较小；梁达到极限荷载后承载力下降较为缓慢，表明新旧混凝土界面粘结良好。其原因是凿坑处理采用“梅花”布置方式，使得HFRPC与旧混凝土间的粘结作用分布更加均匀，界面粘结更好。采用玄武岩纤维布缠绕的梁，当达到极限荷载后，承载力下降最为缓慢。玄武岩纤维布阻止了弯曲裂缝的扩展，增大了梁的抗弯刚度。

3 荷载理论计算与分析

3.1 基本假定

1)加固梁截面应变符合平截面假定，即截面应变沿梁高度为线性分布；

2)原混凝土梁开裂后不考虑其抗拉强度，HFRPC开裂后需考虑纤维的抗拉作用；

3)新旧混凝土界面无滑移，纵筋与基体间无滑移。

3.2 材料本构关系

3.2.1 普通混凝土拉压本构关系

普通混凝土受压应力-应变关系采用《混凝土结构设计规范》(GB50010)[5]的模型，即

(1)

(2)

(3)

式中：σc表示压应变为εc时混凝土的应力；fc为混凝土的轴心抗压强度；ε0为压应力达到fc时混凝土压应变，当计算的ε0值小于0.002时，取为0.002；εcu为混凝土极限压应变，当计算的εcu值大于0.003 3时，取为0.003 3；fcu为混凝土立方体抗压强度；n为系数，取为2.0。

混凝土抗拉应力-应变模型：

(4)

式中：σt表示拉应变为εt时混凝土的拉应力；ft,c为混凝土的轴心抗拉强度，计算时取2.7 MPa；εtu,c为拉应力达到ft,c时混凝土的拉应变，计算时取为0.000 1。

3.2.2HFRPC受拉本构关系

HFRPC拉应力-应变曲线采用简化模型，分为直线上升段和水平段[6-8]，曲线函数为式(5)。

(5)

式中：ER为HFRPC的弹性模量，取36 000 N/mm2；ftr,R为HFRPC的抗拉强度，计算时取5.6 MPa；εtr,R为HFRPC开裂时的拉应变，取0.000 156；εtu,R为HFRPC极限拉应变，取0.007。

3.2.3 钢筋本构关系

高强钢筋和普通钢筋的应力-应变关系假定为理想弹塑性模型，即

(6)

式中：fy为钢筋屈服强度实测值，普通钢筋取350 MPa，高强钢筋取546 MPa；εy为纵筋屈服应变，普通钢筋取0.001 75，高强钢筋取0.002 73；Es为钢筋的弹性模量，均取200 GPa。

3.3 开裂弯矩

梁开裂前基本上处于弹性工作阶段，应力与应变成正比，受压区与受拉区混凝土应变分布接近直线分布，受拉区HFRPC应力分布形式为梯形分布。由于HFRPC弹性模量大于普通混凝土，在新旧混凝土界面应力有突变，如图5所示。

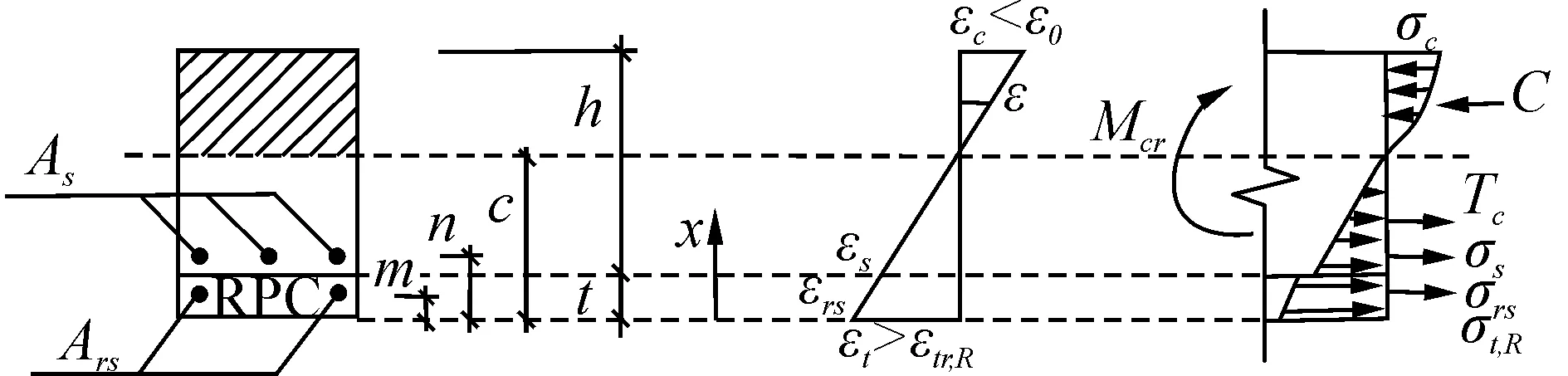
图5 RPC初裂时梁截面应力应变分布图Fig. 5 Distribution of stress and strain on the section when HFRPC cracking

梁将要开裂时，截面上不同高度处混凝土应力分布为

(7)

根据力的平衡∑N=0有

(8)

将式(7)代入式(8)，得

(9)

式中：Es为普通钢筋弹性模量；As为原混凝土梁内底部纵筋截面面积；Ers为高强钢筋弹性模量；Ars为HFRPC加固层内纵筋截面面积；m为高强钢筋中心距梁底的距离；n为原混凝土梁内底部纵筋中心距梁底的距离；ccr为初裂时中和轴高度；t为HFRPC加固层厚度；εtu,c为普通混凝土受拉开裂时的应变，值为0.000 1。

由式(9)求出梁底部开裂时截面中和轴高度ccr，再由力矩平衡∑M=0有

(10)

将求出的中和轴高度ccr代入式(10)中，化简整理可得加固梁的开裂弯矩：

(11)

由式(11)计算了梁的开裂弯矩，列于表4。可见除了梁R-40-C试验值与理论值相差较大外，其余理论计算值与试验值吻合良好。

3.4 屈服弯矩

试验过程中首先是HFRPC中的纵筋屈服，紧随其后原混凝土梁内纵筋屈服。由于原纵筋与新纵筋不同时屈服，为了便于计算和留有一定的安全度，在计算梁的屈服弯矩时，对高强钢筋屈服强度乘以0.9的折减系数。计算屈服荷载时，根据受压区混凝土的压应变是否大于ε0，分为以下两种情况。

3.4.1 受压区混凝土压应变εc<ε0

此时梁截面应力、应变分布如图6所示。HFRPC加固层中纵筋屈服时，HFRPC加固层已开裂，由HFRPC抗拉应力-应变曲线可知此时HFRPC加固层的拉应力为定值ftr,R，不考虑梁受拉区原混凝土的抗拉作用，梁截面的应力分布为

(12)

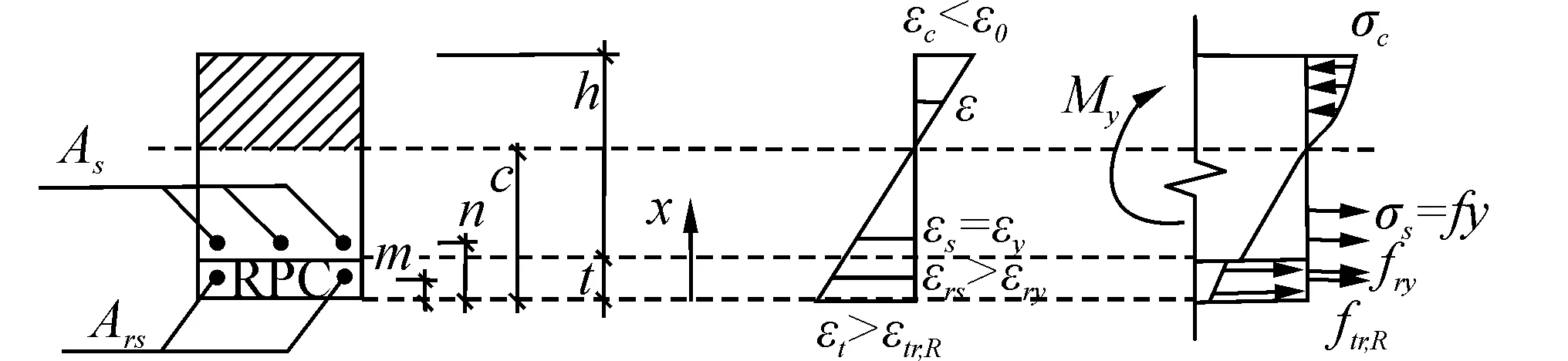
图6 钢筋屈服时梁截面应力应变分布图Fig. 6 Distribution of stress and strain on the section at yielding

由图中的几何关系知：

(13)

(14)

由力的平衡关系，∑N=0有

(15)

式中：fy、fry分别为原混凝土梁内底部纵筋和HFRPC加固层内纵筋屈服时的应力。

由式(15)可以求出纵筋屈服时截面中和轴高度cy。由力矩平衡∑M=0，化简整理可得HFRPC加固梁的屈服弯矩My为

(16)

3.4.2 受压区混凝土压应变ε0<εc<εcu

此时梁截面应力、应变分布如图7所示。受压区混凝土压应变较大，梁截面的应力分布为

(17)

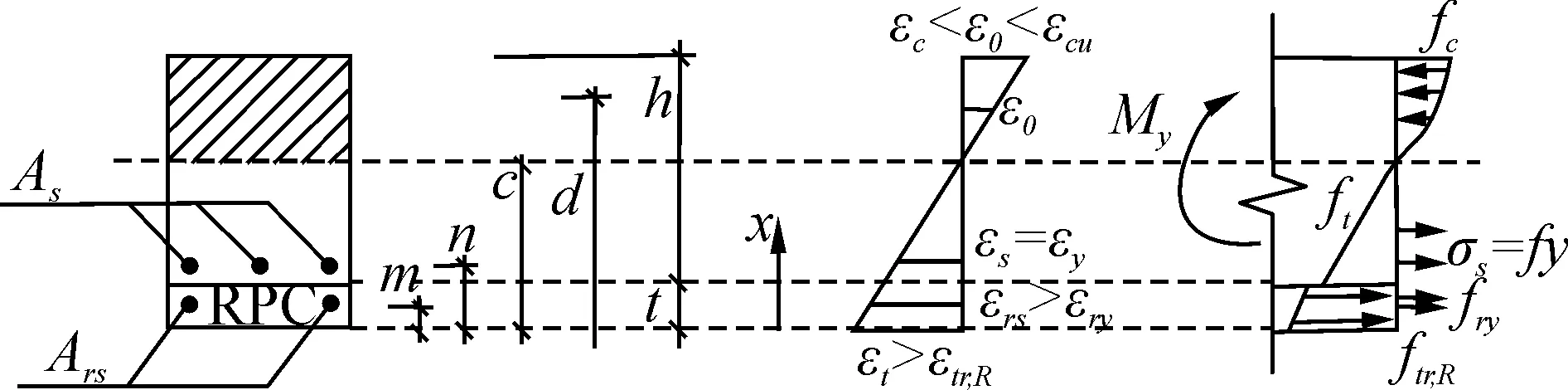
图7 钢筋屈服时梁截面应力应变分布图(ε0<εc<εcu)Fig. 7 Distribution of stress and strain on the section at yielding(ε0<εc<εcu)

从图7中的几何关系有：

(18)

从而得：

(19)

由力的平衡关系，∑N=0可得出：

(20)

由式(20)可以求出梁纵筋屈服时截面中和轴高度cy，由力矩平衡∑M=0，经化简整理可得加固梁的屈服弯矩为：

(21)

据平截面假定得出梁顶受压应变εc>ε0，本试验结果属于第2种情况，按照第2种情况计算得出的屈服弯矩列于表4。计算值与试验值的比平均为0.96，计算值与试验值吻合较好。

3.5 极限荷载计算

梁内纵筋全部屈服后，梁进入第3阶段，其应力、应变分布如图8所示。

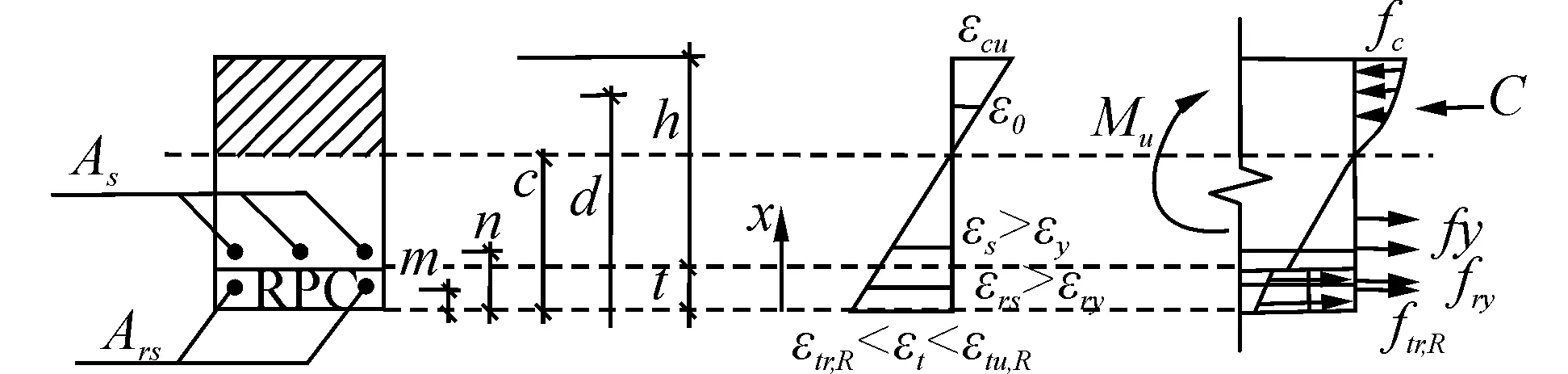
图8 极限状态时梁截面应力应变分布图Fig. 8 Distribution of stress and strain on the section at limit state

当受压区混凝土压应变达到极限压应变后，梁截面开始发生破坏；梁截面混凝土和HFRPC的应力分布方程为：

(22)

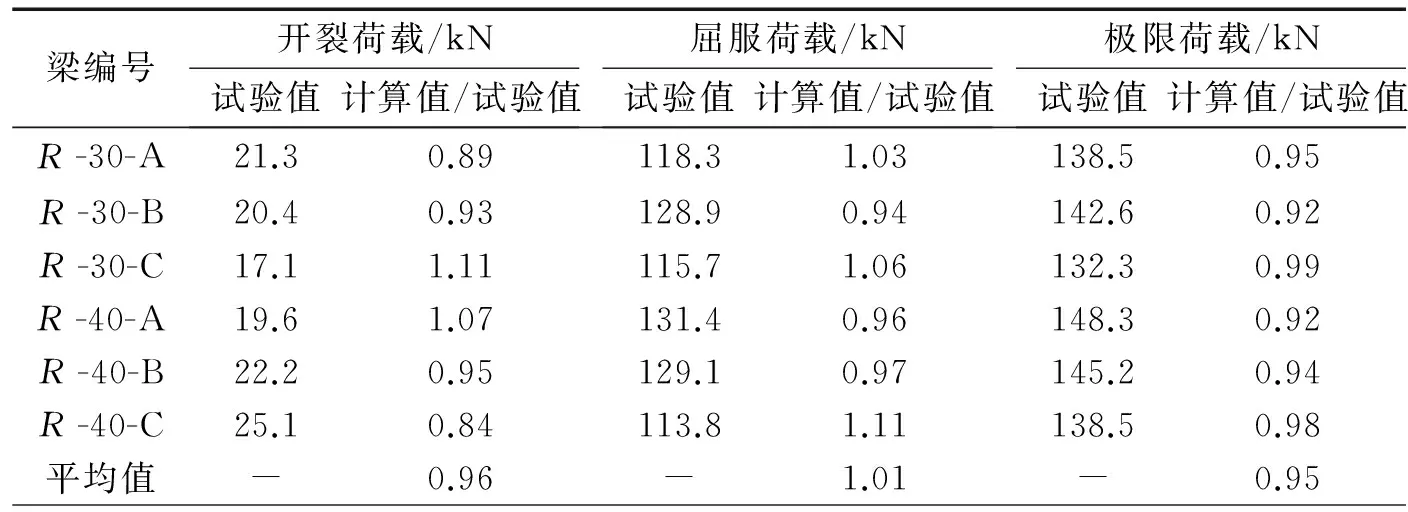
表4 理论计算与试验结果对比

为求出受压区混凝土的压应力，需知道受压混凝土应力达到fc时的截面高度d，此时有：

(23)

据力的平衡条件∑N=0，将应力、应变表达式代入平衡方程中，经化简整理可求出梁达到极限荷载时梁的中和轴高度cu为：

(24)

再据力矩平衡∑M=0，化简整理可得HFRPC加固梁的极限弯矩为：

(25)

由式(25)求得的梁极限荷载值列于表4，可见试验值均大于理论计算值，相对误差均在5%左右，计算值相对较准确，所建立公式可用于预测HFRPC加固梁的极限承载力。

4 结论

1)使用HFRPC加固RC梁能够有效提高梁的承载能力，经加固后梁的承载力约为原混凝土梁2倍，当梁产生较大挠度时仍可以保持较高承载力。

2)HFRPC加固层与原混凝土之间界面粘结良好，未发生脱离破坏。新旧混凝土界面采用凿坑处理的效果优于凿沟处理方式，前者梁抗弯承载力较高，且峰值荷载后承载力下降较缓慢。

3)HFRPC中的高强钢筋发生屈服，发挥了高强钢筋的优势。

4)HFRPC加固层厚度由30mm增大到40mm，抗弯承载力提高约5%。HFRPC加固梁受弯过程中产生了较多细而密的小裂缝，而未加固梁的弯曲裂缝条数较少，宽度大。

5)建立了HFRPC加固混凝土梁抗弯承载力公式，理论计算值与试验结果较吻合。

[1]BUYUKOZTURK O, GUNES O, KARACA E. Progress on understanding debonding problems in reinforced concrete and steel members strengthened using FRP composites[J]. Construction and Building Materials, 2004, 18(1): 9-19.

[2]LI V C, WU H C. Conditions for pseudo strain-hardening in fiber reinforced brittle matrix composites[J]. Applied Mechanics Review, 1992, 45(8): 390-398.

[3]徐世烺, 李庆华. 超高韧性水泥基复合材料在高性能建筑结构中的基本应用[M]. 北京: 科学出版社, 2010: 147-160. XU Shilang, LI Qinghua. Basic application of ultra high toughness cementitious composites in advanced engineering structures[M]. Beijing: Science Press, 2010: 147-160.

[4]郑建岚, 罗素蓉, 王雪芳. 高性能混凝土抗裂性能研究[J]. 工程力学, 2008, 25(S2): 71-98. ZHENG Jianlan, LUO Surong, WANG Xuefang. The research on the cracking behavior of high performance concrete[J]. Engineering Mechanics, 2008, 25(S2): 71-98.

[5]中华人民共和国住房和城乡建设部. GB 50010-2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011. Housing and Urban-rural Development of the People's Republic of China. GB50010-2010, Code for design of concrete structures [S]. Beijing: China Architecture and Building Press, 2011.

[6]TAYLOR C W, MONTOYA K F, JUREGUI D V, et al. Feasibility analysis of using UHPC in prestressed bridge girders[C]//New York: ASCE Structures Congress, 2011.

[7]GRAYBEAL B. Flexural behavior of an ultrahigh-performance concrete I-girder[J]. ASCE Journal of Bridge Engineering, 2008, 13(6): 602-610.

[8]GRAYBEAL B A. Characterization of the behavior of ultra-high performance concrete[D]. Maryland: University of Maryland, 2005:23-96.

Flexural performance of reinforced concrete beams reinforced with hybrid fiber reactive powder concrete

DENG Zongcai，ZHANG Wuchen

(Beijing Key Laboratory of Earthquake Engineering and Structural Retrofit, Beijing University of Technology, Beijing 100124, China)

In order to study the retrofitting effects of hybrid fiber reinforced reactive powder concrete (HFRPC),the flexural behaviour of reinforced concrete (RC) beams reinforced with HFRPC was investigated by experiment and theory, then compared with reinforced concrete beams without retrofitting. Seven test beams were designed and made, one of which was not retrofitted, while the other 6 were retrofitted with HFRPC. The test variables include thickness of HFRPC, HFRPC and concrete interfacial bonding method, retrofitting fiber, and so on. The test results show that the reinforced concrete beam strengthened with HFRPC exhibits improved bearing capacity and decreased deformation. The HFRPC retrofitting layer bonds well with concrete, no debonding failure happens. While there are numerous cracks on the HFRPC reinforcement layer, crack width is significantly decreased.Gouged beams have larger bearing capacity than those with troughs. The superior performance of high-strength steel set in HFRPC is fully utilized. Beams with a 40 mm thickness retrofitting layer have larger capacity than 30 mm beams, about 5% better flexural performance. Adopting fiber cloth wraps to retrofit new and old concrete beams can effectively prevent crack propagation, and thus slowing down loss of ultimate load bearing capacity. Through theoretical analysis, a formula for the calculation of HFRPC beam crack load, yield load, and ultimate load is provided. Finally,the experimental results match well with the theoretical predictions.

reactive powder concrete; ultra-high performance concrete; hybrid fiber; retrofitting; sectional enlargement method; flexural performance;reinforced concrete

2014-04-21.

时间：2015-07-28.

国家自然科学基金资助项目(51378032)；教育部博士点基金资助项目(20131103110017)；北京自然科学基金资助项目(8142005).

邓宗才(1961-)，男，教授，博士生导师.

邓宗才，E-mail：Dengzc@bjut.edu.cn.

10.3969/jheu.201404065

TU375

A

1006-7043(2015)09-1199-07

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150728.1419.007.html