双层同轴腔交叉耦合的新型腔体滤波器

谢振雄，林福民，赵培伟

(1.广东工业大学 物理与光电工程学院，广东 广州510006;2.广东通宇通讯设备有限公司广东中山市528400)

随着现代通讯技术的日益发展，频谱越来越拥挤，而电磁波频谱是有限的，需按应用加以分配，由此更加凸显滤波器性能的重要性，而滤波器性能优劣将直接影响到通信系统的质量和频谱资源的利用效率.金属腔体滤波器由于其电磁屏蔽性好、承受功率高、插损低、高带外抑制、频带宽等特点，自然成为了移动通信基站滤波器的首选［1-2］.

目前，移动通信基站滤波器都是单层结构，通过相邻同轴腔之间或者不相邻腔之间进行交叉耦合在传输通带边制造传输零点，从而实现高带外抑制，这类移动通信基站滤波器在国内外学术文献中已经有了大量相关研究论文［3-6］，但至今尚未见到有关双层结构的同轴腔体滤波器的研究论文和相关产品.

在单层滤波器中，最常用的是通过加一根飞杆实现两个腔体之间的电容耦合［7-8］，从而达到在左边制造零点的目的;可是飞杆加工麻烦，不易调节.本人提出一种新的电容耦合结构，无需增加飞杆，即可在通带的左边实现传输零点.在单层双排结构的同轴腔滤波器中，一个单腔最多只有4个面与相邻腔进行耦合，而双层结构滤波器可以利用单腔的上下面与相邻腔进行耦合，从而可以比同轴腔更好地实现广义契比雪夫滤波器特性［9］.其次，双层滤波器还能使滤波器的结构更加紧凑，形状更加多样化，以满足各类通信系统的要求.

1 双层同轴腔与并排同轴腔体的滤波性能对比

为了比较上下双层腔体和并排同轴腔体的耦合系数方面的差异，本节把双层同轴腔与并排同轴腔的单个腔体尺寸都设计为长70 mm、宽60 mm、高30 mm，腔体内设为真空，加载电容半径为10 mm、高20 mm，并排同轴腔耦合窗的高度设为30 mm，上下腔之间耦合孔宽度设为4 mm，并且两个模型的单个腔体以耦合窗或耦合孔为中线互相对称.不使用调谐螺钉，从而保证双层腔体和并排同轴腔腔体大小、加载电容都一样的情况下，只改变它们之间耦合窗口宽度a或耦合孔长度b的尺寸，使用HFSS进行两腔之间耦合系数的仿真，可以看出耦合系数kij随耦合窗宽度a或耦合孔长度b的变化.并排同轴腔的结构和仿真结果如图1和图2所示.双层同轴腔的结构和仿真结果如图3和图4所示.

图1 并排同轴腔结构Fig.1 Structure of double row coaxial cavity

图2 并排同轴腔耦合系数与耦合窗口宽度a变化图Fig.2 Variation of double row coaxial cavity coupling coefficient and window width“a”

图3 双层腔体结构Fig.3 Structure of two-layer coaxial cavity

图4 双层腔之间耦合系数随耦合孔长度b变化图Fig.4 Variation of two-layer coaxial cavity coupling coefficient by coupling aperture length“b”

由耦合系数的仿真结果如图2和图4所示，腔体大小等其他条件一样的情况下，并排同轴腔体之间的耦合系数在0.001至0.045之间，而双层腔体之间的耦合系数为0至0.18这个范围内，可以看出双层腔体之间耦合系数的跨度范围远超同轴腔体.利用软件(couple-filter)分析，双层腔体之间的耦合系数完全可以满足宽频带和高带外抑制广义契比雪夫滤波器的设计要求.由于耦合系数的跨度范围大，上下双层腔体的带宽潜力也远远大于并排同轴腔体.

2 双层多腔体滤波器的结构设计

2.1 以耦合双间隙腔为基本单元的多腔体滤波器的设计

以耦合双间隙腔为基本单元设计了一款多腔体体滤波器［10］，其拓扑结构如图5所示，拓扑结构中1、2、3、4的位置与实物图中单腔的位置一一对应，入射波由腔1进入，由腔4出去，两腔之间的耦合全是电感耦合，由零点判别理论可知［11］，它不产生传输零点.图6为仿真模型图，实物图如图7所示，这款腔体滤波器包括两个双间隙耦合腔，以及输入、输出两个同轴端口，每个耦合双间隙谐振腔由上下两个完全对称的矩形谐振腔组成，上下两个矩形谐振腔之间通过开耦合槽来实现耦合，相邻两个双间隙谐振腔之间通过一个开孔的金属耦合壁实现耦合;用于输入和输出的两个同轴线端口分别设置在第一个双间隙腔的上腔和第二双间隙腔的下腔，以达到充分利用4个单腔谐振模式的目的.

图5 4阶腔体滤波器拓扑结构Fig.5 Topology of four-cavity filter

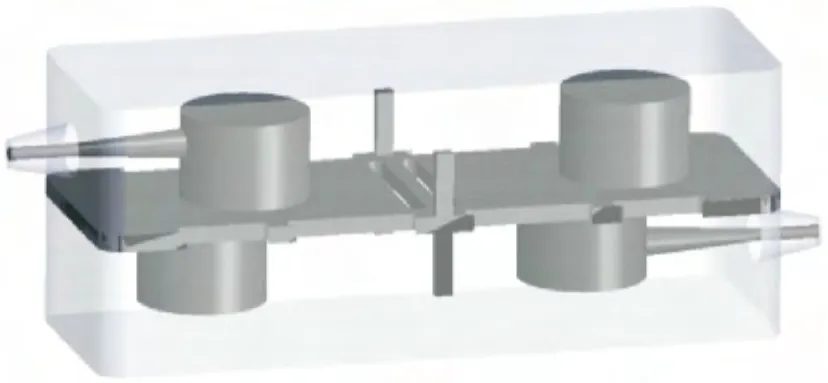
图6 双层4阶腔体滤波器模型Fig.6 Model of two-layer and four-cavity filter

图7 滤波器实物图Fig.7 Picture of filter

S11为反射系数，S21为传输系数，由测试结果图8可知，这款腔体滤波器的带宽有75 MHz，带内的回波损耗均在15 dB以下，由于未设置零点，带外抑制稍微差一点，但可以看出，双层结构的腔体滤波器可以实现很好的滤波性能.

2.2 双层四腔交叉耦合腔体滤波器的设计

设计了一个四阶双层交叉耦合结构的滤波器，其拓扑结构原理如图9所示;1、2、3、4分别代表腔体滤波器的4个腔，入射波由腔体1进，由腔体4出，腔体1与腔体4之间为电容耦合，其他腔之间的耦合为电感耦合.

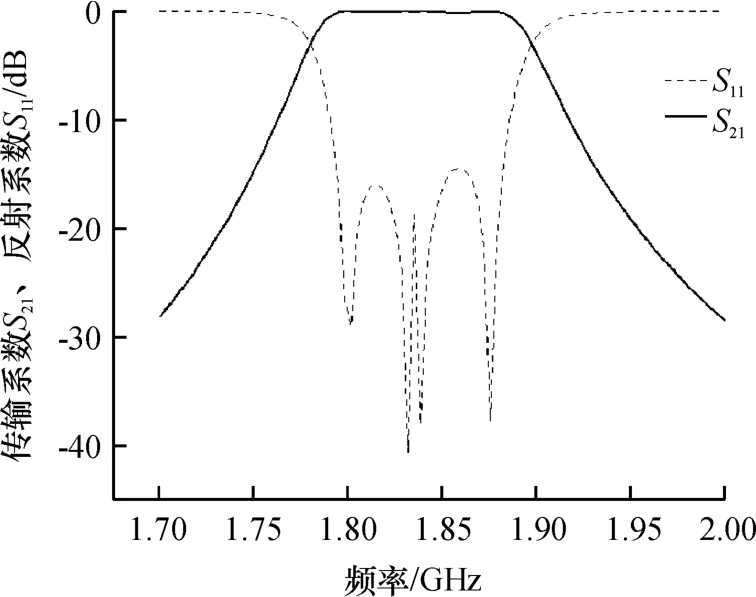
图8 实物测试结果图Fig.8 Results of the test

图9 4阶交叉耦合拓扑结构Fig.9 Cross-coupling topology with four-cavities

由电路常识可知，通过电感的S21会产生－90°的相位差，通过电容会产生+90°的相位差.当频率低于谐振频率时，腔体呈容性，高于谐振频率时，腔体呈感性.根据耦合拓扑结构和零点判别理论［11］，综合出这个拓扑结构的的相移路径(见表1)，可知，这个四阶的拓扑结构将在通带的左右各产生一个零点.

表1 相移路径Tab.1 Total phase shift for the paths

本文理论设计的滤波器带宽为1.805～1.880 GHz，左边零点位置为1.78 GHz，右边零点的位置为1.95 GHz，回波损耗在20 dB，利用软件(couplefilter)［12］分析得出各个单腔理论上的谐振频率(见表2)和它们之间的耦合系数等(见表3).

表2 各腔之间的谐振频率Tab.2 Resonate frequency of single cavity

表3 各腔之间的耦合系数Tab.3 Coupling coefficient

表2可知4个单腔的谐振频率，由表3可知f14的耦合系数为负号，可知腔体1与腔体4之间是电容耦合，其他腔之间的耦合都为电感耦合，另外，腔体1与腔体3之间并没有任何耦合.本文假设当腔体1与3之间有一个类似于1与4之间的电容耦合，通过软件(couple-filter)增加一个耦合矩阵系数k13，发现S21曲线图并未有什么较大的变化;由此可知即使1与3之间有微弱电容耦合，对整体的滤波性能影响不大，这将为下面滤波器结构的设计提供依据.

2.3 单腔的确定

设计单腔时，主要考虑的是它的无载Q值和谐振频率，由于是用于大功率(1.8 kW)的滤波器.综合考虑，选定了单腔(长70 mm，宽60 mm，高30 mm，内圆柱半径为10.8 mm，调谐螺钉半径为2 mm)，腔体Q值确定为5 800.抽头位置的高度为17 mm，采用圆盘耦合与环耦合相结合的耦合方式.

2.4 两腔之间系数的仿真

腔体滤波器的主要耦合方式有电耦合、磁耦合和混合耦合，当两个谐振频率相同的谐振腔发生耦合的时候，它们的谐振频率会分开，那么它们之间的耦合系数与谐振腔频率f1、f2有如下关系［13-14］:k12=.因此，对两个相邻谐振腔进行本征频率分析，得到上下两个腔体的耦合窗宽度和长度对应的耦合系数曲线(如图2和图4所示).

2.5 滤波器的仿真

经过上面的步骤，就可以在HFSS中建模仿真，经过进一步的调节，可以获得比较理想的特性曲线，最终确定结构尺寸.腔体外壳总的尺寸为长183 mm，宽60 mm，高64 mm，调谐螺钉半径选2 mm，去掉外壳，里面结构的尺寸如图10所示，单位为mm.下层第一个腔与下层第二个腔对应着拓扑结构中的1与4，上层第一个腔与上层第二个腔对应这拓扑结构中的2与3.腔体2与腔体1、腔体4之间形成交叉耦合，其中腔体2与腔体4之间是通过开一个‘丄’字形金属架来实现电感耦合的，腔体1与腔体4之间是通过开一个较大的耦合孔(如图11)实现微量的电容耦合.腔体2与腔体3、腔体4之间形成交叉耦合，从而在左右两边各实现一个传输零点，具体见结构尺寸图10、模型图11和仿真结果图12.

图10 滤波器的结构尺寸Fig.10 Size of filter

图11 四阶双层交叉耦合结构滤波器模型Fig.11 Model of two-layer coaxial cavity cross-coupling filter with four cavities

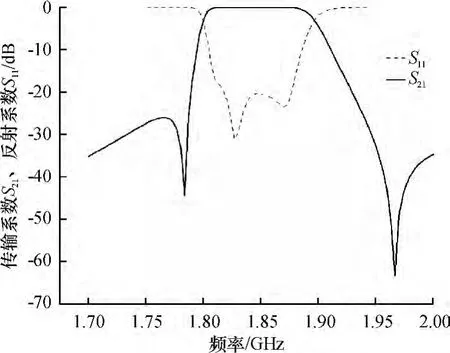
图12 双层4阶结构模型仿真图Fig.12 Simulation of two-layer filter with four cavities

由仿真结果可以看出通带左右各产生了一个零点，腔体滤波器的带宽有75 MHz，带内的回波损耗大约在－20 dB，左边的零点大概在1.775 GHz，右边的零点在1.97 GHz，基本接近理论的参数，由于设置了传输零点，对比图8，可以看出，它的带外抑制要好很多，由此可知，四阶双层腔体交叉耦合滤波器有着良好的滤波性能，也验证了软件(couple-filter)的准确性.

2.6 对比单层同轴腔体滤波器

单层同轴4阶腔体滤波器与双层4阶腔体滤波器S21曲线对比如图13所示，从中可以看出，双层4阶腔体滤波器在带外抑制、插入损耗等各项指标接近或者达到单层4阶腔体滤波器的效果，而且在双层结构中，只需要开一个耦合斜槽就可以实现电容耦合，这比单层同轴腔体滤波器通常通过加一根飞杆来实现电容耦合简单方便得多.并且由于双层同轴腔结构可以充分利用单个腔体上下表面来实现开孔耦合，从而可以使它的结构排列形式更加多样化，甚至立体化，将能更好地利用有限的空间.

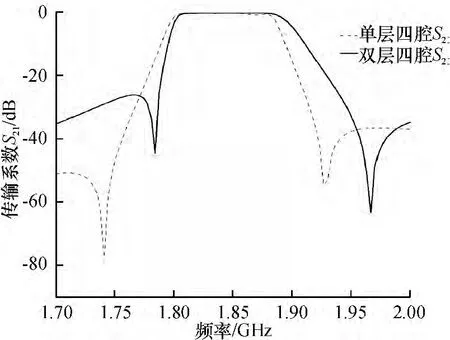
图13 单层4阶腔体滤波器与双层4阶腔体滤波器的仿真对比Fig.13 Simulated comparison of single layer filter with four cavities＆two-layer filter with four cavities

3 结束语

本文针对单层同轴腔体结构滤波器不能很好实现复杂的交叉耦合，结构不紧凑等缺点，在耦合双间隙腔的基础上，通过理论分析，利用三维仿真软件HFSS，设计了一种双层结构交叉耦合的新型腔体滤波器，这种双层交叉耦合结构的新型腔体滤波器具有频带宽、带外抑制好、通带插损低、结构紧凑且形状多样化、易于实现交叉耦合等诸多优点.在双层同轴腔之间进行交叉耦合以实现宽频带和高带外抑制的做法是国内外首次使用的创新性方法，此项研究将为以后发展更多层立体结构的腔体滤波器或多工器提供理论和技术支持.

［1］李军，贾宝富，张国柱，等.高温度稳定性腔体滤波器研究［J］.微波学报，2008，24(5):145-148.Li J，Jia B F，Zhang G Z，et al.Study on high-temperature stability of cavity filters［J］.Journal of Microwaves，2008，24(5):145-148.

［2］Cameron R J，Harish A R，Radcliffe C J.Synthesis of advanced microwave filters without diagonal cross-couplings［J］.Microwave Theory and Techniques，IEEE Transactions on，2002，50(12):2862-2872.

［3］Wang Y，Yu M.True inline cross-coupled coaxial cavity filters［J］.Microwave Theory and Techniques，IEEE Transactions on，2009，57(12):2958-2965.

［4］Hunter I C，Billonet L，Jarry B，et al.Microwave filtersapplications and technology［J］.Microwave Theory and Techniques，IEEE Transactions on，2002，50(3):794-805.

［5］Wang H，Chu Q X.An inline coaxial quasi-elliptic filter with controllable mixed electric and magnetic coupling［J］.Microwave Theory and Techniques，IEEE Transactions on，2009，57(3):667-673.

［6］Hoft M，Yousif F.Orthogonal coaxial cavity filters with distributed cross-coupling［J］.Microwave and Wireless Components Letters，IEEE，2011，21(10):519-521.

［7］Hoft M，Burger S，Magath T，et al.Compact combline filter with improved cross coupling assembly and temperature compensation［C］∥Microwave Conference，2006.APMC 2006.Asia-Pacific.［S.l.］:IEEE，2006:781-784.

［8］Hoft M.Tunable Capacitive Coupling for Cavity Resonator Filters［C］∥GermanMicrowaveConference，2009.［S.l.］:IEEE，2009:1-4.

［9］Cameron，Richard J.General coupling matrix synthesis methods for Chebyshev filtering functions［J］.Microwave Theory and Techniques，IEEE Transactions on，1999，47(4):433-442.

［10］赵培伟，林福民.耦合双间隙腔的滤波特性研究［J］.微波学报，2012(S1):202-206.Zhao P W，Lin F M.Research on filter characteristic of coupling double-gap cavity［J］.Journal of Microwaves，2012(S1):202-206

［11］Thomas J B.Cross-coupling in coaxial cavity filters-a tutorial overview［J］.Microwave Theory and Techniques，IEEE Transactions on，2003，51(4):1368-1376.

［12］汪雪刚，吴多龙，苏华锋，等.同轴腔体带通滤波器的设计与实现［J］.广东工业大学学报，2012，29(4):54-58.Wang X G，Wu D L，Su H F，et al.Design and implement action for a coaxial cavity band-pass filter［J］.Journal Guangdong University of Technology，2012，29(4):54-58.

［13］Hong J S，Lancaster M J.Couplings of microstrip square open-loop resonators for cross-coupled planar microwave filters［J］.Microwave Theory and Techniques，IEEE Transactions on，1996，44(11):2099-2109.

［14］Hong J S，Lancaster M J.Microstrip Filter for RF/Microwave Applications［M］.New York:Wiley，2001:421-429.