基于多通信半径的加权DV-Hop定位算法*

刘士兴,黄俊杰,刘宏银,易茂祥

(合肥工业大学电子科学与应用物理学院,合肥 230009)



基于多通信半径的加权DV-Hop定位算法*

刘士兴*,黄俊杰,刘宏银,易茂祥

(合肥工业大学电子科学与应用物理学院,合肥 230009)

DV-Hop定位算法是无线传感器网络中一种常用的基于非测距的定位技术,该算法使用平均跳距表示实际距离,在实际应用中造成很大的误差和节点能耗。为此,分析了加权DV-HOP定位算法,并在加权算法基础上,引入多通信半径广播方法细化节点间的跳数,最后提出了一种基于加权DV-HOP的改进型RWDV-Hop定位算法。仿真结果证明,加权DV-HOP在定位精度上比DV-HOP算法提高了7.3%,改进型RWDV-HOP在定位精度上比加权DV-HOP算法提高了6.7%。

无线传感器网络;DV-Hop定位算法;信标节点;加权算法

近年来,随着低功耗嵌入式技术,微机电系统MEMS(Micro-Electro-Mechanism),无线通信技术SOC(System on Chip)和无线通信(Wirless Communication)的飞速发展,无线传感网络技术应运而生[1]。无线传感器网络WSN(Wireless Sensor Network)是一种自组织的网络,具有低功耗,低成本,体积小以及分布式等特点。无线传感器网络是信息感知的一场技术革命,是21世纪重要的技术之一。因此,无线传感器网络成为了国内外学术界的研究热点。

在无线传感器网络中,传感器节点的位置信息是至关重要的,没有位置信息的监测,采集到数据也就没有了实际意义。因此,在无线传感器网络中,确定事件发生的位置是至关重要的。只有传感器节点的位置信息是确定的,才能获得事件发生的具体位置,从而采取何种方式或者决策。基于以上的分析,传感器网络节点定位技术是当今国内外学者研究的热点和重点。

根据定位机制,将现有的定位算法分为两种,即基于测距的定位算法(range-based)和与距离无关(range-free)的定位算法[2]。前者需要额外增加硬件来测量相邻节点间的绝对距离或者方位,并利用节点间的实际距离来计算未知节点的位置;后者无需额外的硬件测量节点间的绝对距离或方位,而是利用节点间的估计距离计算未知节点的位置。常用的与距离相关的定位技术有RSSI、TOA、TDOA和AOA。这类算法定位精度相对较高,但是成本与能耗开销也较大。与距离无关的定位算法利用网络的连通性进行定位,常用的有质心算法、DV-Hop[3]、Amorphous[4]、APIT[5]等,这类算法成本和功耗较低,应用更加广泛。

DV-Hop算法是目前应用最广泛的定位算法之一,针对DV-Hop算法改进研究,本文提出了提高节点定位精度的加权DV-Hop算法和降低功耗的基于节点密度的定位算法。

1 DV-HOP算法

DV-Hop定位算法是由Niculescud等人提出的一种基于距离矢量计算跳数的算法。其基本思想是将未知节点到信标节点之间的距离用平均跳距和两者之间跳数的乘积表示,具体步骤如下[6]:

①信标节点信息泛洪广播和所有节点获取距离信标节点的最小跳数。信标节点采用泛洪广播方式将其位置信息采用分组形式传递给其邻居节点,广播的信息包格式为:{Idi,xi,yi,Hopsi},其中包含了该节点的标识Idi、位置坐标(xi,yi)以及跳数信息Hopsi,初始Hopsi的值为0。接收到此数据的每个节点将此信息记录下来,然后继续向其邻居节点广播,每广播一次就将Hopsi加1,并将分组信息以{Idi,xi,yi,Hopsi}的格式存储到自己的数据表中。当节点接收到有相同Id的数据包时,对两个数据包中的Hopsi进行比较,如果新的跳数小于原表中保存的跳数,则用新的跳数替换节点中的信息,这就意味着找到了一条更短的到达该信标节点的路径。如果新的跳数大于节点中的跳数,则丢弃该数据包,也不再进行转发。

②计算未知节点与信标节点的估计距离。经过第1步后,每个信标节点获得了其他信标节点的位置和最小跳数。这时通过式(1)计算网络中平均每跳的距离。

(1)

式中:(xi,yi),(xj,yj)为信标节点i,j的坐标,hi为信标节点i与j(i≠j)之间的跳段数,HopSize为求出的平均跳距。

③信标节点将平均跳距广播到网络,通过式(2)计算未知节点到信标节点的估计距离du,i。

du,i=HopSize·hu,i

(2)

当未知节点得到3个或者更多节点之间的距离后,再通过三边测量法[7]或者极大似然估计等数学方法计算未知节点的坐标。

2 加权DV-Hop算法

在实际使用中,DV-Hop算法的定位精度受到节点密度及其分布情况影响。网络中信标节点的密度越大,分布越合理,则定位精度越高,反之则定位误差大。

2.1DV-Hop算法误差分析

在实际使用中,部署信标节点的成本较高,因而信号节点的总数不会很多。另外,节点通常是随机放置在探测环境中,难以保证信标节点分布的合理性[8-9]。综上,实际使用中,DV-Hop定位算法会有很大的定位误差。

DV-Hop定位算法使用跳段数与平均每跳距离的乘积来得到未知节点与信标节点的估计距离。这种估算方法有时候会有很大误差,例如图1对应的网络拓扑结构:

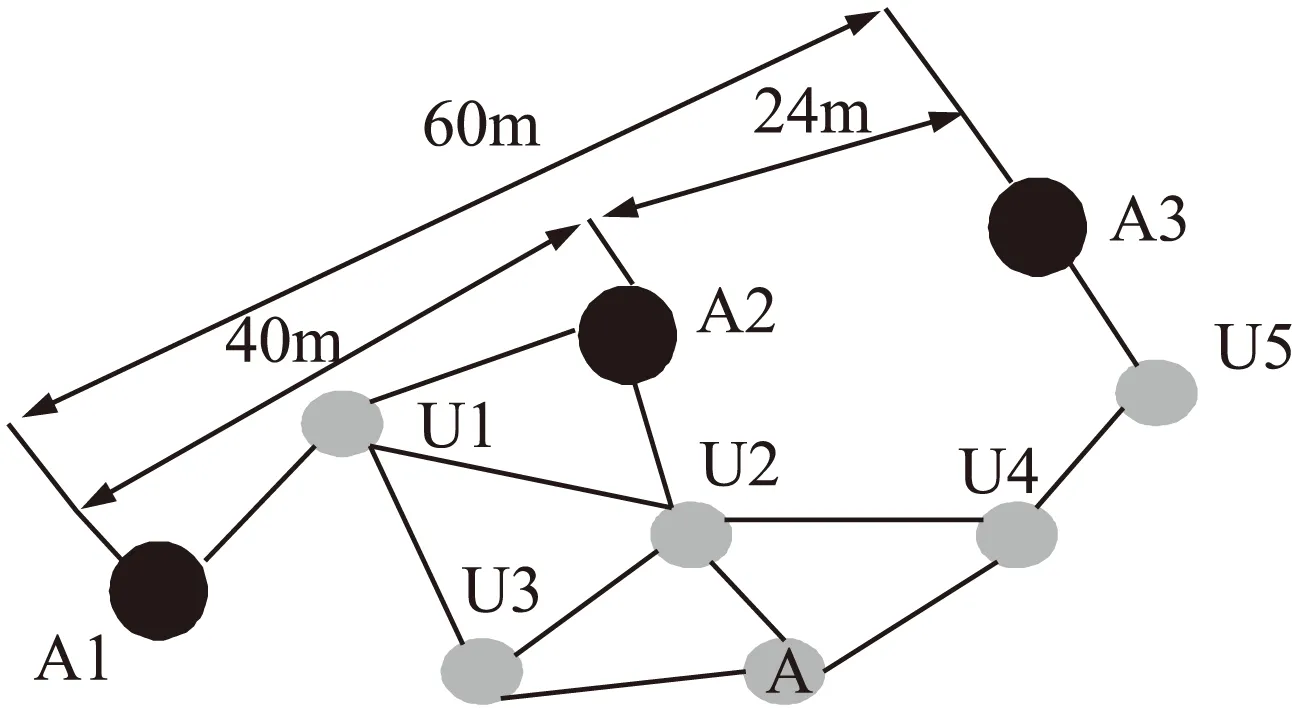
图1 DV-Hop误差分析

图1中,A1、A2和A3为信标节点,U1、U2、U3、U4、U5和A为未知节点。对于未知节点A,由于A2离它最近,所以A应该从A2获取HopSize值。由式(1)得HopSize=(40+25)/(2+5)=10.7,那么3个信标节点与A之间的距离分别为A1:10.7×3,

A2:10.7×2,A3:10.7×3。但是A与3个信标节点的真实距离分别为:50、40和50 m,这使得定位误差非常大。在该网络中,A2与A3真实距离很小,只是略大于通信半径,用A2与A3来估算每跳距离,所得的误差就非常大。

2.2 加权DV-Hop算法

针对上文中提到的关于DV-Hop定位算法中使用相同的平均跳距来计算未知节点到信标节点间距离的定位误差问题,有些学者提出了加权DV-Hop定位算法[10-11]。该算法的基本思想是在DV-Hop定位算法中,通过加权系数的大小体现不同信标节点对未知节点位置坐标运算中的影响力大小,然后通过加权平均跳距估算未知节点的位置。实际使用中,不同信标节点的加权系数Wi通过式(3)确定:

(3)

式中:ni表示信标节点i与未知节点之间的跳数,

根据式(4),得未知节点的加权平均跳距为:

(4)

使用加权后的平均跳距,代入DV-Hop定位算法的第3步,计算出未知节点到信标节点之间的距离,再通过三边测量法或者极大似然估计等数学方法计算出未知节点的坐标。

3 改进加权DV-Hop算法

3.1 加权DV-Hop算法误差分析

在DV-Hop和加权算法中,计算跳数的时候,只要节点在信标节点通信半径R以内,无论远近跳数都为1跳,则该算法计算出的平均跳距误差将会很大。如图2所示,未知节点U1到未知节点U2的距离比节点U2到信标节点A的距离小的多,而在加权DV-Hop算法中,将U1到U2和U2到A的跳数都记为1跳,因此在这种情况下计算平均跳距将产生很大的误差[12]。

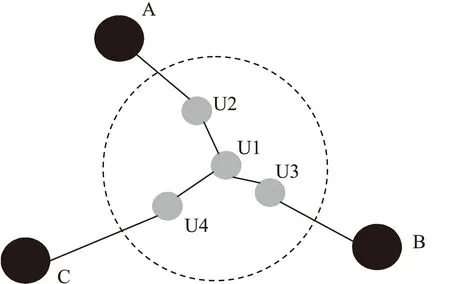
图2 节点分布拓扑结构

3.2 基本思想

根据前文分析,通信半径和信邻节点是加权DV-Hop定位算法中的重要两个因素。因此,如果能够得到信标节点与其邻居节点之间更准确的距离,无疑能够提高所有未知节点的定位精度。本文参考文献[13],对每个信标节点引入多通信半径广播数据,细化信标节点与邻居节点之间的跳数。

鉴于通信半径R是对所有节点而言是相对固定的,因此信标节点以通信半径R广播数据时,邻居节点的跳数记为1,然后节点以不同的通信半径广播数据,不同的通信半径代表不同的跳数,这样可以细化信标节点与邻居节点之间的跳数。

设信标节点的通信半径为R,信标节点与其邻居节点之间的实际距离为d,跳数为h,若节点以通信半径R/n广播数据,i为小于n的整数,则通过不同的通信半径广播数据之后,跳数h为:

(5)

该算法使加权DV-Hop定位算法的跳数值不再是整数,而是小数,这有效提高了跳数值的准确性,从而降低了定位误差。

3.3 改进算法的具体步骤

(1)计算信标节点与邻居节点之间的跳数

网络启动时,信标节点首先以通信半径R/n向网络广播数据,同时把接收节点与发送节点之间的跳数记为1/n跳。数据包格式同DV-Hop定位算法。经过时间T之后,信标节点再以通信半径2R/n向网络广播数据,接收到信标节点信号的节点首先查询是否记录过该信标节点的跳数信息,如果没有,将该未知节点与锚节点之间跳数记为2/n,如果有,则不改变跳数信息,并将信息转发。以此类推,最后信标节点以通信半径R广播数据,收到信标节点信号的节点首先查询是否记录过该信标节点的跳数信息,如果没有,将该未知节点与锚节点之间跳数记为1,如果有,则不改变跳数信息。这样通过不断的转发,所有节点都能得到与锚节点之间的最小跳数。

(2)计算各锚节点之间的平均跳距

参考加权DV-Hop定位算法,利用步骤(1)得到的跳数信息,通过平均跳距公式和加权系数,计算出各锚节点之间的加权平均跳距。

4 算法仿真验证

采用MATLAB软件对上述算法进行仿真,并对仿真数据进行分析[14]。仿真环境为100m×100m的正方形区域,区域中随机分布100个节点。在相同的信标节点数条件下,进行100次重复实验取平均值的方法,对定位误差进行评估。假设未知节点的估算位置为(xc,yc),节点的实际位置为(xi,yi),则未知节点的定位误差为[15-16]:

(6)

式中:R为节点的通信半径,N为未知节点的个数。

图3为通信半径R为20m时,信标节点以R/2、R/3、R/4 3种不同通信半径广播数据时,节点定位的误差仿真图。

从图3可以得出,信标节点以四通信半径广播数据时,节点的定位误差最小,三通信半径次之,两通信半径的定位误差最大。例如,当信标节点个数为16时,n值取4及四通信半径时,节点的定位误差为32.1%,而在节点以三通信半径和两通信半径广播数据时,节点的定位误差分别为34%和38.1%。由此,可以得到,n值越大,节点通信半径越小,跳数划分的越细,节点的定位误差越小。

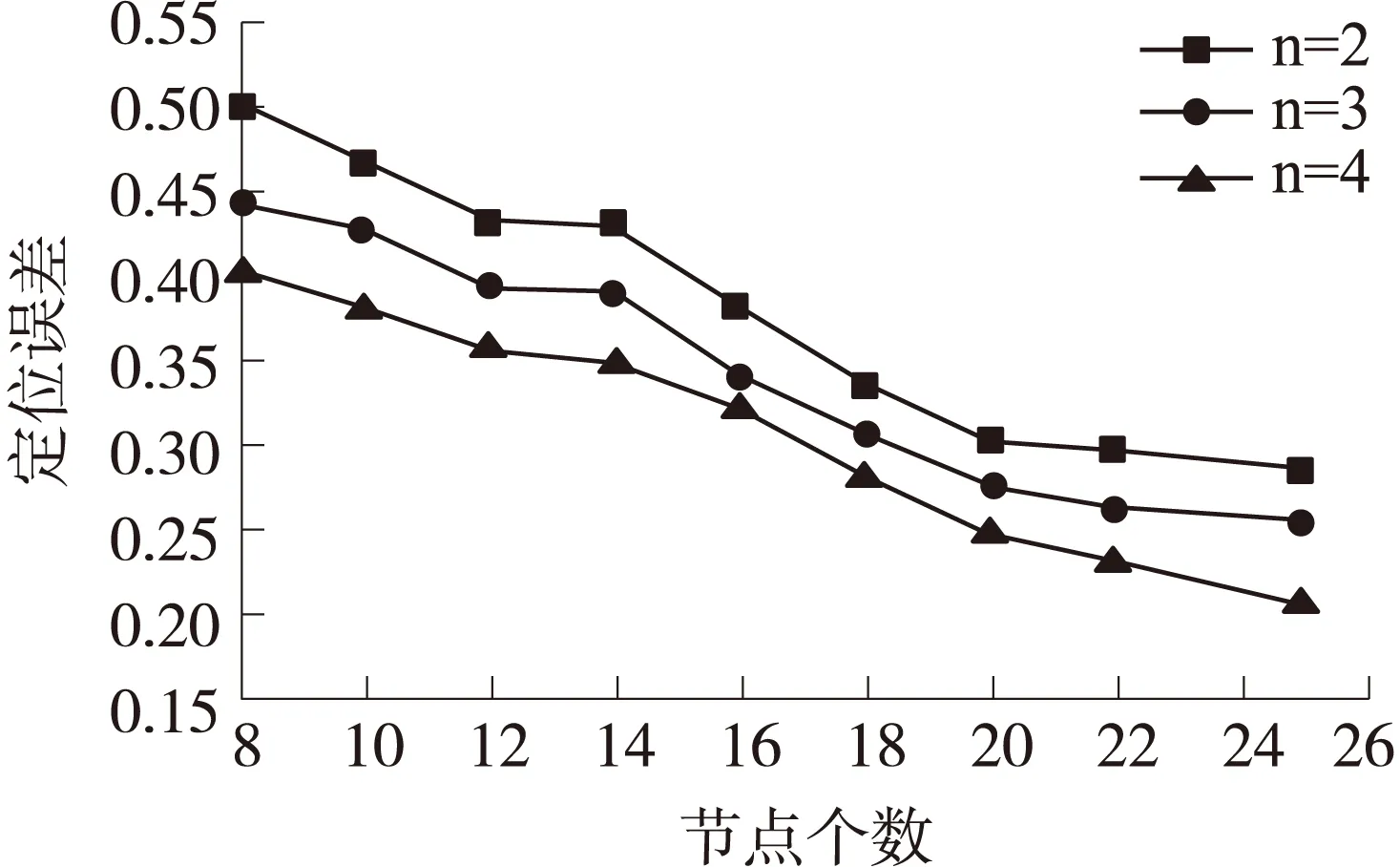
图3 不同通信半径时的定位误差(R=20 m)

图4和图5分别是节点通信半径为20m和25m时,本文提出的多通信半径定位算法(RWDV-Hop算法)、加权DV-Hop算法和DV-Hop算法在锚节点数目变化时的定位误差仿真图。

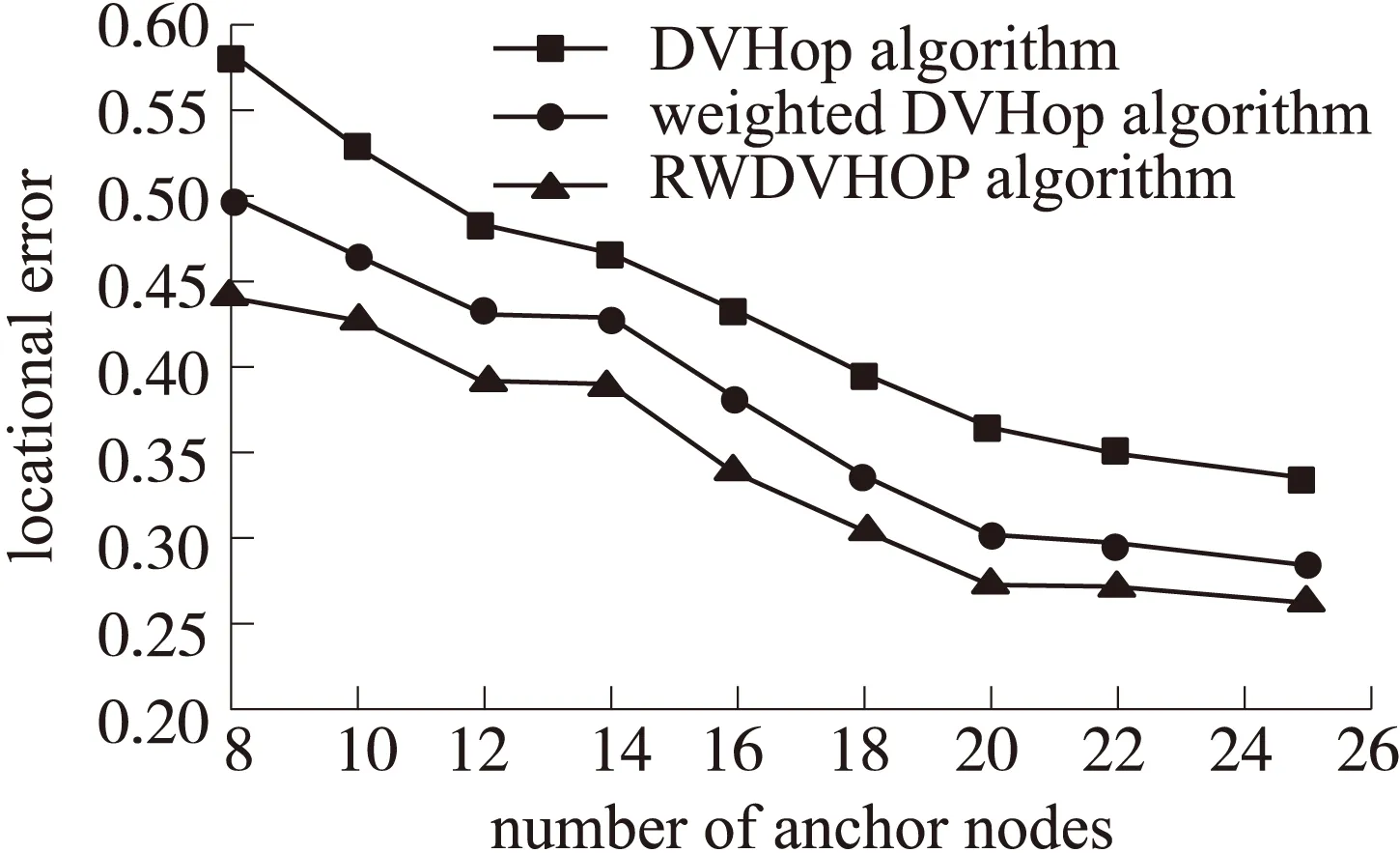
图4 节点个数与定位误差的关系(R=20 m)

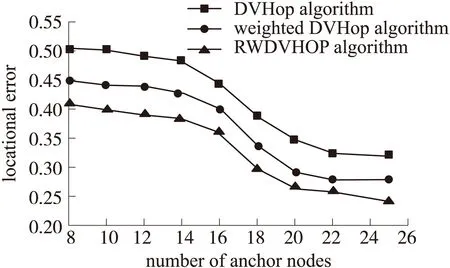
图5 节点个数与定位误差的关系(R=25 m)

从图中可以看出,在相同的通信半径和锚节点比例下,RWDV-Hop定位算法定位精度最高,加权DV-Hop定位算法次之,DV-Hop定位算法定位误差最大。

例如:从图5可以看出,当节点通信半径为25 m,锚节点数目为14时,DV-Hop定位算法的定位误差为48.2%,加权DV-Hop定位算法的定位误差为42.1%,而RWDV-Hop定位算法的定位误差为38.2%。

从图4可以看出,当节点通信半径为20m,锚节点数目为14时,DV-Hop定位算法的定位误差为46.8%,加权DV-Hop定位算法的定位误差为43.1%,而RWDV-Hop定位算法的定位误差为39.3%。当锚节点数目为16时,加权DV-Hop定位算法比DV-Hop定位算法的定位误差小了4.4%,而RWDV-Hop定位算法的定位误差比加权DV-Hop定位算法的定位误差小了3.5%。

由此说明本文提出的基于多通信半径的定位算法,在相同的环境以及相同的锚节点数目条件下,该算法相对于加权DV-Hop算法和DV-Hop定位算法,在对未知节点的位置计算上更加准确即该算法的定位精度最高。

图4和图5比较发现,当节点通信半径增大,定位误差降低。这是因为,通信半径影响节点的连通度,会对节点间的跳数及节点的平均跳距计算产生影响。

6 结论

本文介绍了现有的DV-Hop定位算法,分析了该算法存在定位精度低缺陷。加权DV-Hop定位算法通过加权系数,修正了平均跳距,有效的降低了定位误差。本文提出的RWDV-Hop算法,使用多个通信半径广播自身的分组信息,从而获得未知节点与信标节点之间更精确的跳数,从而计算更加精确的加权平均跳距。利用MATLAB软件进行仿真,仿真结果表明本文提出的RWDV-Hop算法比DV-Hop定位算法和加权DV-Hop定位算法在定位精度上有明显的提高。

本文讨论的算法都是在理想状态下进行的仿真,但现实环境中往往会因为温度、湿度以及大气压强等因素对节点定位造成影响。如何在考虑这些影响因素的前提下来提高节点的定位精度还有待进一步的研究。

[1] Bulusu N,Heidemann J,Estrin D. GPS-less Low Cost Outdoor Localization for Very Small Devices[J]. IEEE Personal Communication,2000,7(5):28-34.

[2] 孙利民,李建中,陈渝. 无线传感器网络[M]. 北京:清华大学出版社,2005:135-155.

[3] Lin Jinchao,Chen Xiaobing,Liu Haibo. Iterative Algorithm for Locating Nodes in WSN Based on Modifying Average Hopping Distances[J]. Journal on Communications,2009,10(30):107-133.

[4] Nagpal R. Organizing a Global Coordinate System from Local Information on an Amorphous Computer[D]. AI Memo 1666,MIT AI Laboratory,August 1999:257-262.

[5] He Tian,Huang Chengdu,Blum B M,et al. Range-Free Localization Schemes in Large Scale Sensor Networks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking,MOBICOM’2003. San Diego(CA,USA),2003. New York(NY,USA):ACM Press,2003:81-95.

[6] 李晓维,徐勇军,任丰原. 无线传感器网络技术[M]. 北京:北京理工大学出版社,2007:247-259.

[7] Cao Yu,Chen Xiupeng,Yu Yang,et al. Range-Free Distance Estimate Methods Using Neighbor Information In Wireless Sensor Networks[C]//Proc IEEE 70th Vehicular Technology conference Fall(VTC 2009-Fall),2009,9:1-5.

[8] Tian Shuang,Zhang Xinming,Wang Xinguo,et al. A Selective Anchor Node Localization Algorithm for Wireless Sensor Networks[J]. International Conference on Convergence Information Technology(ICCIT),2007(11):164-168.

[9] Liu Shaoqiang,Pang Xinmiao,Fan Xiaoping. Improved DV-Hop Algorithm for Higher Positioning Accuracy[J]. Chinese Journal of Sensors and Actuators,2010,8(23):1179-1183.

[10] 冯江,朱强,吴春春. 改进的DV-Hop定位算法研究[J]. 计算机工程,2012,38(19):74-77

[11] Chen Hongyang,Sezaki,K,Ping Deng,et al. An Improved DV-HOP Localization Algorithm for Wireless Sensor Networks[C]//Industrial Electronics and Applications. ICIEA 2008. 3rd IEEE Conference,2008,6:1557-1561.

[12] Erchin Serpe din,Qasim M Chaudhari. Synchronization in Wireless Sensor Networks[J]. Science Press,2011:124-128.

[13] Li Juan,Liu Yu,Qian Zhihong,Improved DV-Hop Localization Algorithm Based on Two Communication Ranges for Wireless Sensor Network[J]. Journal of Jilin University,2014,3(44):25-29.

[14] 温江涛,范学敏,吴希军. 基于RSSI跳数修正的DV-Hop改进算法[J]. 传感技术学报,2014,27(1):113-117.

[15] 夏少波,邹建梅,朱晓丽,等. 基于跳数区域划分的DV-Hop改进算法[J]. 传感技术学报,2014,27(7):964-949.

[16] 江禹生,冯砚毫. 一种新的DV-Hop定位算法[J]. 传感技术学报,2010,23(12):1815-1819.

刘士兴(1969-),男,毕业于中国科学技术大学,现任合肥工业大学副教授。主要研究方向为无线传感网络,多参数火灾探测;

黄俊杰(1991-),男,安徽明光人,合肥工业大学硕士在读,主要研究方向物联网、无线传感器网络、火灾探测等,askao_know@163.com;

刘宏银(1988-),男,安徽天长人,合肥工业大学硕士在读,主要研究方向物联网、无线传感器网络、火灾探测等,liuhongyin115@163.com。

An Improving DV-Hop Algorithm Based onMulti Communication Radius*

LIUShixing*,HUANGJunjie,LIUHongyin,YiMaoxiang

(School of Electronic Science and Applied Physics,Hefei University of Technology,Hefei 230009,China)

DV-Hop is one of the most common used localization algorithms in range-free algorithms. This algorithm uses hop distance instead of the actual distance,which results in localization error and large energy consumption. The weighted DV-Hop algorithm is analyzed,and an improved algorithm based on the weighted DV-Hop is proposed. The improved algorithm broadcasts the data using multi communication radius and refines the hops to reduce the location error. The average hop distance depended on the neighbor nodes and the communication radius is corrected in this new algorithm. The simulation shows that the improvement of the improved algorithm on the positioning precision is 6.7%.

wireless sensor networks;anchor node;weighted algorithm;DV-Hop

项目来源:国家自然科学面上基金项目(61371025);安徽高校省级自然科学研究重点项目(KJ2012Z316)

2015-01-06 修改日期:2015-02-16

C:7230

10.3969/j.issn.1004-1699.2015.06.018

TN929.52

A

1004-1699(2015)06-0883-05